東南沿海地區(qū)玄武巖殘積土雨水運移特征及滑坡失穩(wěn)數(shù)值模擬

張晨陽，張?zhí)悾瑥?明，孫 強，伍劍波，王赫生

(1.中國地質大學(武漢)工程學院，湖北 武漢 430074；2.中國地質調查局南京地質調查中心，江蘇 南京 210016)

玄武巖殘積土在我國廣泛分布，其性質較為特殊，具有親水性強、高孔隙比、易濕化崩解等特征[1]。大量研究結果表明，玄武巖殘積土本身的微裂隙較多，滲透性強，在降雨入滲過程中，通過裂隙的優(yōu)勢流加速了雨水的入滲，土體含水量逐漸增大，基質吸力隨之降低，抗剪強度減小，最終影響殘積土斜坡的穩(wěn)定[2-3]，導致斜坡失穩(wěn)[4-5]。我國東南沿海地區(qū)玄武巖殘積土斜坡分布較廣，暴雨期間極易失穩(wěn)[6-9]，而該地區(qū)玄武巖殘積土的入滲特性及滑坡失穩(wěn)機制研究程度較低，因此有必要對其進行研究。

殘積土中的降雨入滲過程十分復雜，且在斜坡原位進行觀測較為困難[8]，因此室內(nèi)土柱試驗是研究殘積土降雨入滲特征的重要手段。朱偉等[9]利用土柱實驗探討了降雨強度和時間對土壤水分重分布的影響。Gofar等[10]進行了室內(nèi)土柱實驗，探討了降雨對土壤孔隙水壓力分布的影響。Rao等[11]通過土柱實驗對森林覆蓋土進行了一系列滲透性質的研究，在此基礎上改進了Green-Ampt入滲方程。以上研究采用的均是重塑土，由于天然狀態(tài)下玄武巖殘積土內(nèi)存在大量的殘余結構，采用重塑土必然與真實情況有較大差異[12]；且上述研究中通過土柱實驗獲取的降雨入滲特征未應用到滑坡的穩(wěn)定性分析中。本文以浙江省溫州市馬濟頭玄武巖殘積土滑坡為對象，利用原狀土土柱實驗，獲取中峰型與前峰型兩種降雨工況下玄武巖殘積土的雨水運移特征，獲取最符合玄武巖殘積土入滲特征的土水特征曲線及滲透函數(shù)；然后將上述曲線應用于滑坡的滲流場和穩(wěn)定性變化研究中。

1 馬濟頭滑坡概況

馬濟頭滑坡位于浙江省溫州市大峃鎮(zhèn)馬濟頭村，滑坡整體呈圈椅狀，縱向長約60 m，寬約38 m(圖1)。滑坡所處區(qū)域地貌為低山丘陵，局部地形上陡下緩，前緣高程476 m，后緣高程512 m，相對高差36 m，總體坡向82°。坡體表層覆蓋玄武巖殘積土，層厚3～6 m,紅褐色，原巖結構已不可見，成砂、黏土狀。基巖地層為中生代白堊系朝川組玄武巖，黑褐色，無斑隱晶質結構，氣孔構造。

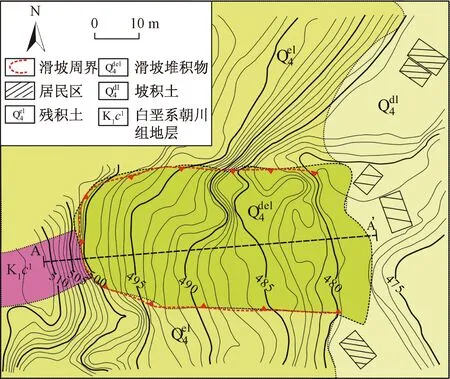
圖1 馬濟頭滑坡平面圖Fig.1 Map of the Majiton landslide

原始斜坡在2016年鯰魚臺風暴雨期間發(fā)生整體滑動，對坡腳32戶居民產(chǎn)生了較大的威脅。由現(xiàn)場勘察資料可知，滑坡上覆的玄武巖殘積土沿著基覆面整體失穩(wěn)，滑面呈圓弧形，在殘積土層內(nèi)。滑坡失穩(wěn)后，整體呈圈椅狀。滑體堆積在坡腳位置，體積約10 000 m3(圖2)。

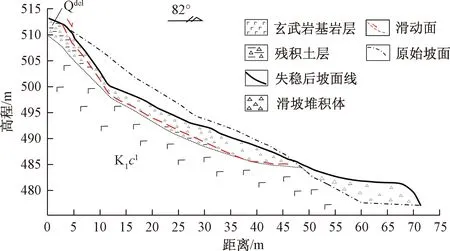
圖2 馬濟頭滑坡A-A′剖面圖Fig.2 Geological profile alonp line A-A′ of the Majitou landslide

2 降雨入滲土柱實驗

為了獲取玄武巖殘積土的雨水運移特征，在坡體取2個原狀土土柱，分別在室內(nèi)進行中峰型與前峰型2種降雨工況下的降雨實驗。

2.1 實驗設計

2.1.1實驗裝置

整個實驗裝置包括模擬降雨系統(tǒng)、土柱裝置和數(shù)據(jù)采集系統(tǒng)。模擬降雨系統(tǒng)包括馬氏瓶和針管式模擬降雨器。降雨強度通過馬氏瓶的高度來控制。經(jīng)過率定，實驗使用的降雨強度10，30 mm/h所對應的馬氏瓶高度分別為150，165 cm。土柱裝置為一圓形有機玻璃筒，直徑30 cm，高度150 cm(圖3)。上部25 cm支撐降雨器，下部125 cm放置原狀土土柱。離土體表層2 cm的位置設有出口A，當降雨強度較大時，土體表層可形成積水，模擬斜坡表面的片流。筒邊壁預設6個方孔，距土體表層深度為10，20，30，45，65，95 cm，以放置體積含水率探針。土柱的底部設置多孔底板和排水孔B，用于排水。

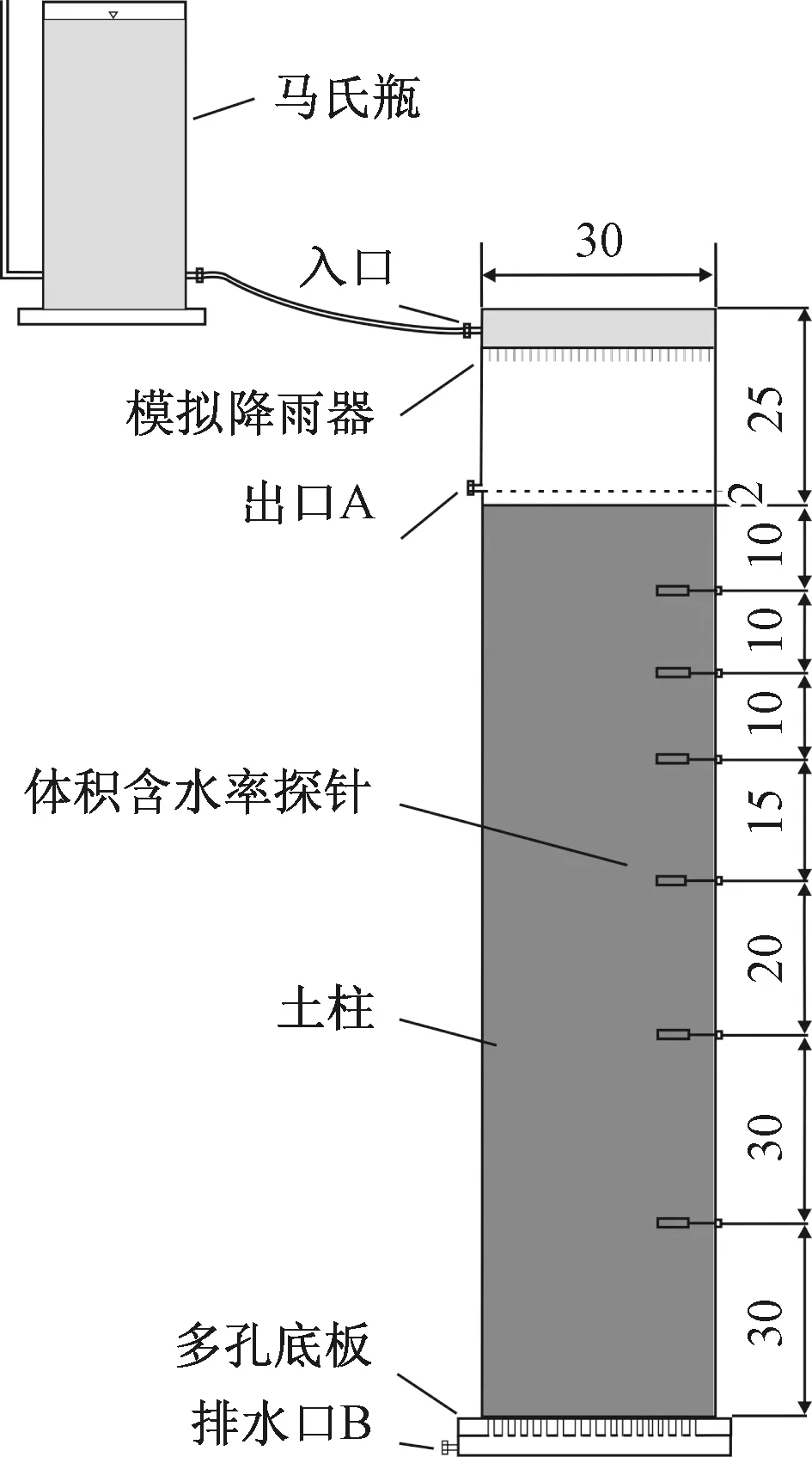
圖3 實驗裝置示意圖(單位：cm)Fig.3 Sketch of the experimental devices

數(shù)據(jù)采集系統(tǒng)包括FDR濕度計、數(shù)據(jù)采集儀和電腦。FDR濕度計的測量范圍為0～100%，誤差為±3%,使用前需通過實驗土樣校正。體積含水率探針插入6個方孔中實時監(jiān)測土壤體積含水率，并通過數(shù)據(jù)采集儀傳輸?shù)诫娔X中。

2.1.2實驗降雨工況

統(tǒng)計研究區(qū)近年來的臺風降雨記錄，總結得到的臺風暴雨期降雨特征如下：①一次降雨事件持續(xù)時間多為3 d左右；②降雨峰值多發(fā)生在第二天，但也有少量發(fā)生在第一天，該天平均降雨量約300 mm，其它兩天降雨量較小，平均降雨量約50 mm；③降雨強度隨著時間分布極不均勻，一天的降雨量往往集中在數(shù)小時內(nèi)[13]。根據(jù)以上特征，我們設置中峰型(ABA)與前峰型(BAA)兩種降雨工況。ABA型降雨工況下，第一天前5小時為降雨期，降雨強度為10 mm/h，其余19個小時為間歇期；第二天前10小時為降雨期，降雨強度為30 mm/h，其余14小時為間歇期；第三天與第一天相同，三天的總降雨量為400 mm。BAA型降雨工況下，第一天前10小時為降雨期，降雨強度為30 mm/h，其余14個小時為間歇期；第二天前5小時為降雨期，降雨強度為10 mm/h，其余19小時為間歇期；第三天與第二天相同。

2.1.3取樣

為了保持殘積土的原始狀態(tài)，取樣時，先將有機玻璃柱緩慢壓入土層，并從四周逐漸開挖，邊壓邊挖，直至設計深度。在滑坡同一位置取1號和2號兩個土柱，取樣完成后用塑料薄膜將其密封，運回實驗室。1號土柱進行中峰型降雨，2號土柱進行前峰型降雨。

2.1.4數(shù)據(jù)采集及處理

實驗過程中，定時采集土柱內(nèi)10，20，30，45，65，95 cm深度處的體積含水率。降雨期采集間隔為1 min，間歇期為30 min。

2.2 結果分析

2.2.1土柱初始孔隙水壓力分布

土體初始的水勢分布反映了其前期的降雨情況，控制著土體的雨水運動特征[14]。實驗開始前利用張力計獲取2個土柱的初始孔隙水壓力分布。2個土柱的初始孔隙水壓力的分布整體較為相似，1號土樣在20 cm深度的孔壓最大，約-26 kPa，其余深度的初始孔壓較為一致，約-28 kPa；2號土樣在10 cm深度的孔壓最小，約-32 kPa，30 cm深度的孔壓最大，約-26 kPa,其余深度的孔壓約-30～-29 kPa。

2.2.2體積含水率變化征

圖4～5分別是ABA和BAA型降雨工況下，土柱內(nèi)不同深度的體積含水率變化曲線。

ABA型降雨工況下，第二天降雨期間，土柱內(nèi)各深度的體積含水率最大，第三天降雨期間大于第一天；降雨間歇期內(nèi)土柱的體積含水率隨降雨天數(shù)的增加逐漸增大，第一天間歇期最小，第三天間歇期最大。土柱內(nèi)10，20，30，45，65，95 cm深度的初始體積含水率分別為32%、32%、30%、33%、32%、34%。第一天降雨3 h內(nèi)，土柱內(nèi)體積含水率從上到下依次增大，20,30,45,65 cm深度增大約5%～8%，10,95 cm深度增大約20%；降雨結束后4 h，20,30,45,65 cm深度體積含水率降低3%～5%，10,95 cm降低約15%。第二天降雨1 h內(nèi)，土柱內(nèi)體積含水率從上到下依次迅速增大，30,45,65 cm深度增大5%～8%，10,20,95 cm深度增大約22%；降雨結束后各深度體積含水率迅速下降，30，45，65 cm深度降低約5%，10，20 cm深度降低約10%，95 cm深度降低約20%。第三天降雨3 h內(nèi)，土柱內(nèi)體積含水率從上到下依次增大，30，45，65 cm深度增大5%～8%，10，20 cm深度增大7%，95 cm深度增大15%；降雨結束后，30，45，65，95cm深度體積含水率降低約5%，10，20 cm深度降低約10%。

圖4 ABA型降雨工況下不同深度土體體積含水率分布Fig.4 Distribution of VWC at different depths in soil column under the central rainfall condition

BAA型降雨工況下，第一天峰值降雨期間各深度體積含水率最大，第三天降雨期大于第二天；降雨間歇期內(nèi)土柱的體積含水率隨著降雨天數(shù)的增加逐漸減小，第一天間歇期最大，第三天間歇期最小。土柱內(nèi)10，20，30，45，65，95 cm深度的初始體積含水率分別為32%、35%、37%、35%、32%、28%。第一天降雨1 h內(nèi)，土柱內(nèi)土體的體積含水率從上到下依次增大，10，20，30，65 cm深度增大18%～20%，45 cm深度增大10%，95 cm深度增大27%；降雨結束后，10，20，30，95 cm深度體積含水率降低10%，45，65 cm深度降低5%。第二天降雨2.5 h內(nèi)，各深度土體從上到下依次迅速增大，10，20 cm深度增大 10%，30，45，65 cm深度增大 5%，95 cm深度增大7%；第二天降雨結束后，土柱內(nèi)各深度的體積含水率迅速下降，10 cm深度降低7%，20，30，45 cm深度降低5%，65 cm深度降低7%，95 cm深度降低10%。第三天降雨2 h內(nèi)，從上到下各深度土體的體積含水率依次增大，10，20，30 cm深度增長5%，65，95 cm深度增長10%；第三天降雨結束后，10，20，30，45，95 cm深度降低5%，65 cm深度降低8%。

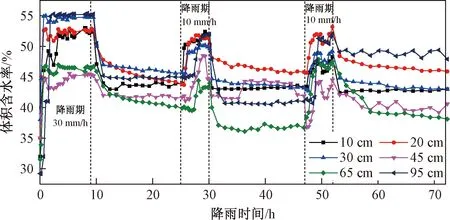
圖5 BAA型降雨工況下體積含水率分布Fig.5 Distribution of VWC at different depths in soil column under the advanced rainfall condition

整體來看，馬濟頭滑坡玄武巖殘積土上部土體的體積含水率增長速率及幅度較大，淺部及深部土體更易達到飽和；且雨水在峰值降雨期間下滲速率十分迅速。

2.2.3濕潤鋒運移特征

本次實驗中，當土柱內(nèi)某深度體積含水率持續(xù)增大且超過3%時，認為是濕潤鋒到達該處的時刻。分別繪制濕潤鋒深度隨時間變化的曲線和濕潤鋒運移速率隨深度變化的曲線(圖6)。

10 mm/h降雨強度期間，2個土柱的濕潤鋒下滲深度與時間均呈線性關系，ABA型降雨工況下下滲速率為8.33×10-5m/s，BAA型降雨工況下下滲速率為9.15×10-5m/s。

圖6 濕潤鋒向下運移速率曲線Fig.6 Velocity curves of wetting fronts

30 mm/h降雨強度期間，濕潤鋒運移速率遠大于10 mm/h降雨期，且濕潤鋒隨著深度增加速率不斷降低。ABA型降雨工的峰值降雨期間，5 cm深度的下滲速率為3.1×10-4m/s，95 cm深度降低75%至7.8×10-5m/s；BAA型降雨工況下的峰值降雨期間，5 cm深度的下滲速率為4.2×10-4m/s，95 cm深度降低85%至6.7×10-5m/s。由此可知，BAA型工況下的峰值降雨期間，隨著深度的增加濕潤鋒運移速率降低的幅度更大。

ABA型降雨工況下的峰值降雨期間，土柱內(nèi)的平均下滲速率約2.4×10-4m/s，是10 mm/h降雨強度期間的2.9倍；BAA型降雨工況下峰值降雨期間，土柱內(nèi)的平均下滲速率約2.0×10-4m/s，是10 mm/h降雨強度期間的2倍。以上表明降雨強度增大時，ABA型降雨工況下濕潤鋒下滲速率的增加幅度更大。

由以上分析可知，馬濟頭滑坡玄武巖殘積土土柱內(nèi)，濕潤鋒在30 mm/h降雨峰值期間的入滲速率遠大于10 mm/h降雨期間，雨水在峰值降雨期間快速進入土柱；峰值降雨期間，ABA型降雨工況下的濕潤鋒平均速率大于BAA型，且前者隨著深度增加速率降低地更慢，更利于雨水入滲。

3 土柱數(shù)值模擬

利用數(shù)值模擬反演上述土柱實驗，以獲取玄武巖殘積土的土水特征曲線及滲透系數(shù)函數(shù)。

3.1 滲流基本理論

在SEEP/W中，二維滲流控制方程如下：

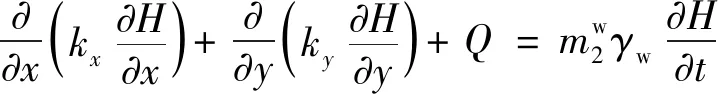
(1)

式中：H——壓力水頭；

kx、ky——滲透系數(shù)，在非飽和土中會隨著基質吸力的變化而變化，即由滲透系數(shù)函數(shù)來定義；

Q——邊界流量；

γw——水的重度。

在SEEP/W中進行滲流數(shù)值模擬時需要土水特征曲線及非飽和滲透系數(shù)函數(shù)。本次研究使用Van Genuchten[15]提出的模型來描述土水特征曲線及滲透系數(shù)函數(shù)。其中，土水特征曲線見式(2)。

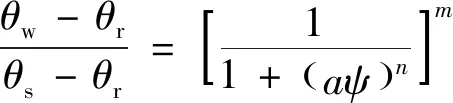
(2)

非飽和滲透系數(shù)曲線見式(3)。

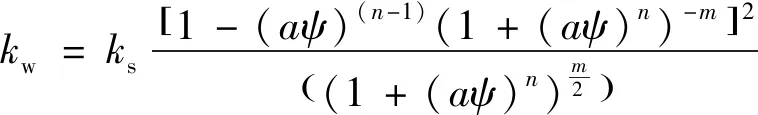
(3)

式中：θs——飽和含水率；

n——曲線基質吸力大于進氣值處斜率相關的擬合參數(shù)；

a——與進氣值有關的擬合參數(shù)；

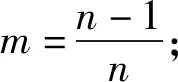
θr——殘余體積含水率。

3.2 參數(shù)反演方法

式(2)、(3)中的飽和體積含水率和飽和滲透系數(shù)ks由室內(nèi)試驗可知為0.60和8.0×10-5m/s。殘余體積含水率取經(jīng)驗值為0.085[15]。要得到馬濟頭玄武巖殘積土的土水特征曲線和滲透系數(shù)曲線，僅需反演得到a、n即可。首先預設a、n的取值范圍，并將其等分。根據(jù)經(jīng)驗值，我們設定a的取值范圍為0.005～0.050，n的取值范圍為0.5～5.0，分別等分為15個值，并交叉取值，共有225種組合。在SEEP/W模塊中，利用上述225組a、n值得到的土水特征曲線和滲透系數(shù)曲線進行土柱降雨入滲數(shù)值模擬。計算數(shù)值模擬所得體積含水率與物理實驗所得結果的均方根誤差(RMSE)，選取誤差最小的一組所對應的a、n值作為反演結果。RMSE的公式見式(4)。

(4)

其中，N為樣本的總數(shù)量，Pi和Qi分別為模擬值與試驗觀察值，這里為體積含水率數(shù)據(jù)。

3.3 土柱降雨入滲數(shù)值模擬

本次降雨入滲土柱數(shù)值模擬根據(jù)物理實驗建立數(shù)值模型，尺寸為 30 cm×130 cm。上部邊界條件為降雨入滲邊界，采用的降雨曲線與室內(nèi)土柱實驗相同。側邊界和底邊界分別為隔水和自由排水邊界。將實驗前獲取的初始孔隙水壓力剖面作為數(shù)值模擬中的初始條件。模擬總時長為3 d，步時10 min，共432步。

經(jīng)過225次模擬，當玄武巖殘積土的a、n值分別為0.030,3.0時，用其得到的土水特征曲線和滲透系數(shù)曲線進行土柱數(shù)值模擬與物理實驗結果之間的RMSE值最小。ABA型和BAA型降雨工況下兩者之間的RMSE值分別為3.66和4.02。反演所得玄武巖殘積土的土水特征曲線與滲透系數(shù)函數(shù)曲線圖7。

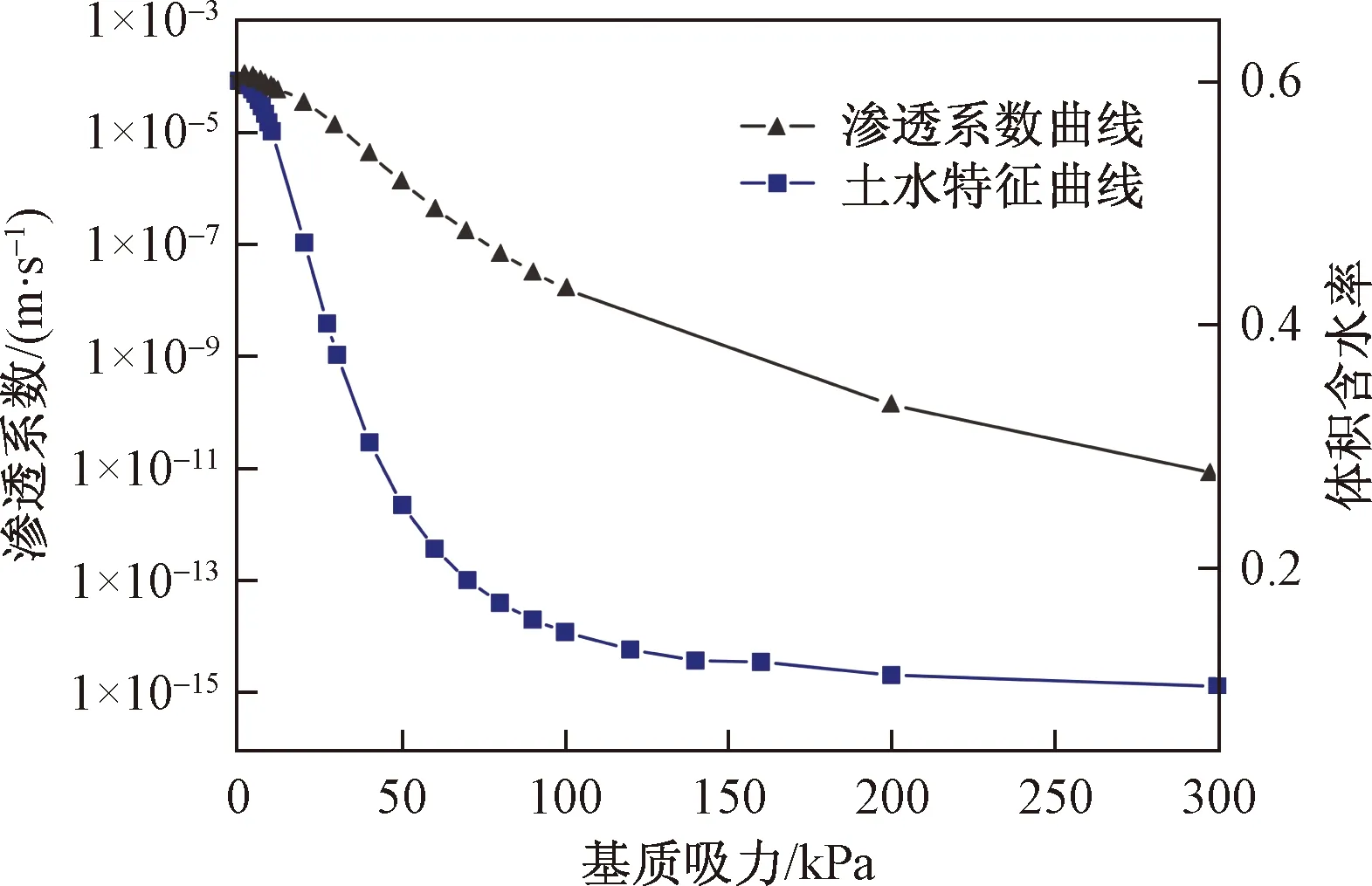
圖7 玄武巖殘積土的土水特征曲線和滲透系數(shù)曲線Fig.7 SWCC and hydraulic conductivity function of the basalt residual soils

4 馬濟頭滑坡數(shù)值模擬

利用上述反演所得的玄武巖殘積土的土水特征曲線和非飽和滲透系數(shù)曲線，首先在Geo-studio軟件中的SEEP/W模塊中模擬得到ABA型和BAA型兩種降雨工況下的滲流場，然后將滲流結果耦合到穩(wěn)定性分析中，得到滑坡的穩(wěn)定性系數(shù)。

數(shù)值計算采用的滲流控制方程見式(1)。飽和-非飽和土抗剪強度理論方程采用Fredlund等[17]提出的雙變量模型，見式(5)。

τf=c′+(σ-μα)tanφ′+(μα-μw)tanφb

(5)

式中：μα-μw——吸力；

φb——受吸力影響的非飽和土抗剪強度參數(shù)；

c′與φ′——飽和土的抗剪強度指標：

τf——剪切破壞面的剪應力。

4.1 數(shù)值模型

根據(jù)圖2所示的馬濟頭滑坡原始斜坡的地質剖面建立其數(shù)值模型(圖8)。初始的地下水位線由勘察資料獲取。為了研究降雨停止后斜坡內(nèi)滲流場和穩(wěn)定性的變化，本次模擬的總時長為7 d，包括降雨期3 d，降雨結束后4 d，步時為1 min，步數(shù)為168步。

模型中包括玄武巖殘積土層及其基巖，兩種材料的水文及物理力學參數(shù)見表1。數(shù)值模型的邊界條件設置如下：①模型兩側地下水位以上為零流量邊界，地下水位以下為定水頭邊界；②底邊界為不透水邊界；③斜坡表面為降雨入滲邊界，前3天降雨情況與土柱實驗相同(降雨邊界不允許積水)，后4天為零流量邊界。

表1 模型中兩種材料的水文和物理參數(shù)Table 1 Hydrological and physico-mechanical parameters of two materials in the numerical model

滑面的前、中、后位置布置c、b、a三個監(jiān)測點(圖8)，監(jiān)測滑帶土的飽和度及孔隙水壓力的變化。

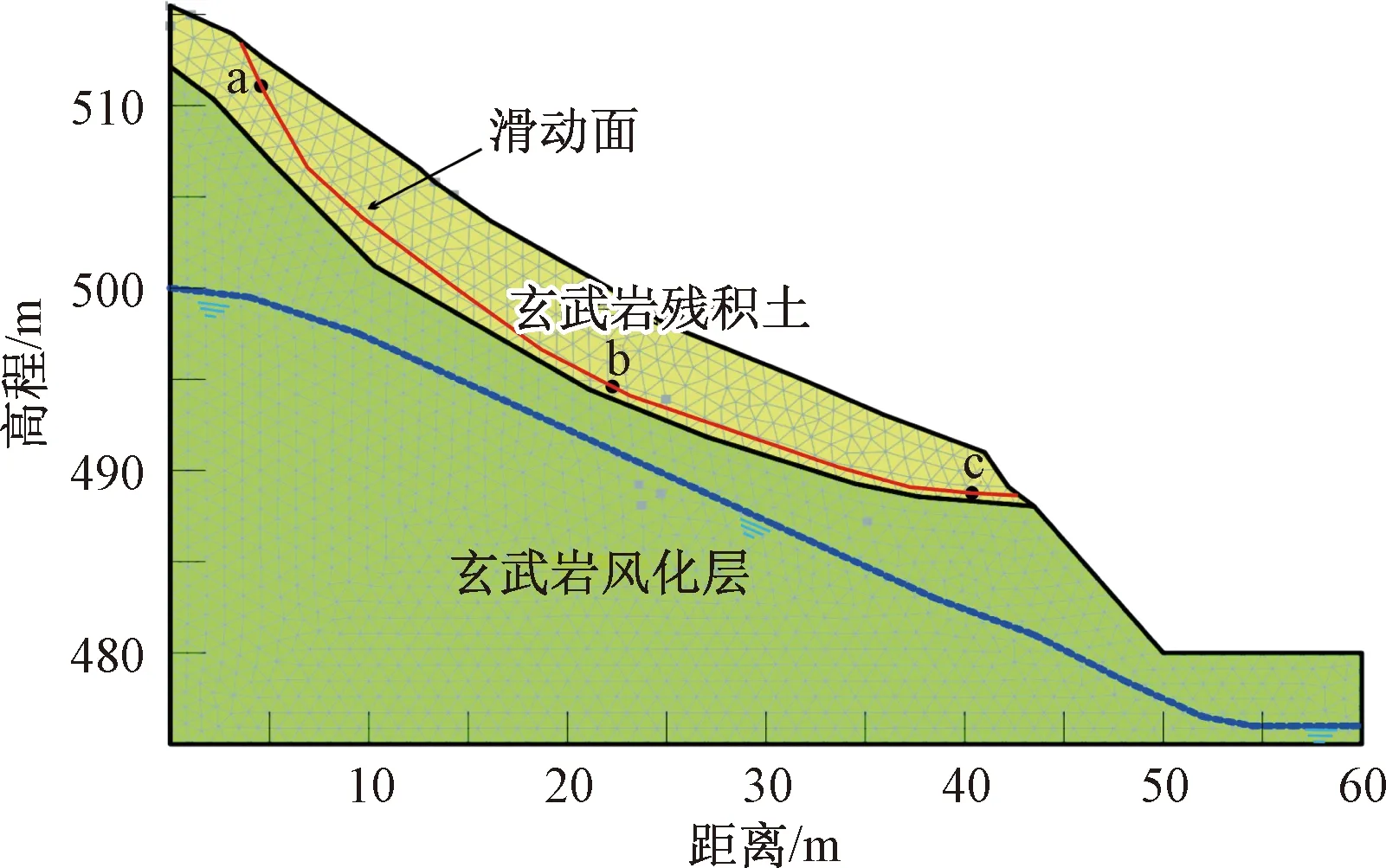
圖8 馬濟頭滑坡數(shù)值模型Fig.8 Numerical model of the Majitou landslide

4.2 結果分析

4.2.1飽和度及孔隙水壓力

圖9是在ABA和BAA型降雨工況下，滑面a、b、c三點的土體飽和度變化曲線。

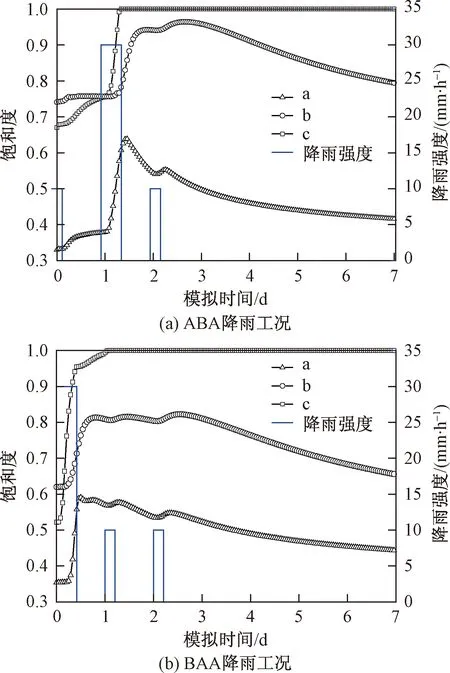
圖9 飽和度變化曲線Fig.9 Curves of saturation

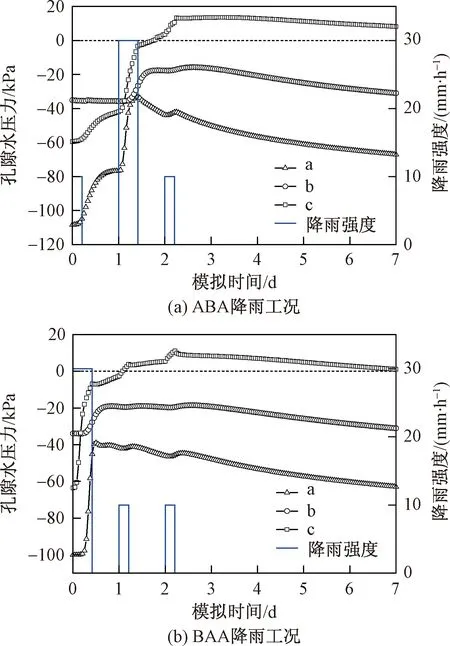
圖10 孔隙水壓力變化曲線Fig.10 Curves of pore-water pressure

由圖9(a)可知，ABA型降雨工況下，第一天降雨5 h后，滑面各點的土體飽和度逐漸增大，但增長幅度僅為0.05～0.1。第二天峰值降雨期，各點飽和度迅速上升，a點由0.35增大至0.65,b點由0.67增大至0.90，c點由0.72增大至完全飽和。峰值降雨結束后，a點的飽和度逐漸降低，第三天降雨期間有小幅回升，隨后持續(xù)下降，第七天降至0.45；b點飽和度在峰值降雨結束后繼續(xù)增大，第三天降雨期間增至0.98，幾乎飽和，隨后逐漸下降，第七天降至0.8；c點飽和度在峰值降雨結束一直飽和直到模擬結束。

由圖9(b)可知，BAA型降雨工況下，第一天峰值降雨期間，滑面各點土體飽和度迅速增長，c點可達飽和，b點增大至0.8，a點增大至0.6。峰值降雨結束后，c點保持飽和直到模擬結束；b點在第二和第三天降雨期間分別有小幅度增長，第三天降雨結束后，逐漸降至0.65；a點的飽和度在峰值降雨結束總體呈不斷下降趨勢，第二天及第三天降雨期有小幅度回升，第三天降雨結束后，逐漸降至0.45。

圖10是在ABA型和BAA型降雨工況下，滑面a、b、c三個位置的孔隙水壓力變化曲線。由圖可知，孔隙水壓力的變化規(guī)律與飽和度幾乎一致。

4.2.2滲流場

圖11是在兩種降雨工況下，滑坡在穩(wěn)定性系數(shù)最小時步(第58時步)的滲流場。斜坡滲流場內(nèi)存在3條地下水位線，下部是坡體的原始地下水位線，在降雨過程中始終沒有變化；滑面上部的地下水位線呈圈閉狀，是由降雨導致的坡體局部滯水，且ABA型工況下的滯水面積比BAA型工況下要大。

圖11 第58時步時斜坡孔隙水壓力分布Fig.11 Distribution of pore-water pressures at 58th step

由以上分析可知，由于馬濟頭玄武巖殘積土土體松散，滲透性較好，在模擬的兩種工況的峰值降雨期間，滑帶土的飽和度和孔隙水壓力迅速增大，坡腳處形成大面積滯水。且ABA型降雨工況下滑帶土的飽和度、孔隙水壓力的值以及坡腳滯水面積均比BAA型大。

4.2.3滑面抗剪強度

圖12是ABA和BAA型降雨工況下，初始及滑體穩(wěn)定性系數(shù)最小時(第58時步)滑帶土的抗剪強度。受降雨入滲的影響，滑帶土的抗剪強度有較大程度的降低，特別是在坡肩和坡腳的位置。滑面中部與坡腳處的土體初始抗剪強度分別約40,30 kPa，在模擬的第58時步，滑面中部土體的抗剪強度降至30 kPa，坡肩處的滑面土體抗剪強度降至17 kPa，坡腳處由于局部滯水存在，可降至15 kPa左右。

圖12 滑面土體抗剪強度Fig.12 Curves of shear strength of the sliding surface

4.3 滑坡失穩(wěn)機制分析

圖13是模擬7 d時間內(nèi)，滑坡穩(wěn)定性系數(shù)變化曲線。坡體的初始穩(wěn)定系數(shù)為1.375，處于穩(wěn)定狀態(tài)，模擬降雨開始后，穩(wěn)定性系數(shù)逐漸降低，且在降雨期明顯比間歇降低速率要快。10 mm/h降雨期，穩(wěn)定性系數(shù)下降速率較慢，而峰值降雨期，穩(wěn)定性系數(shù)迅速降低，兩種工況均在第三天降雨開始的第10小時(第58時步)穩(wěn)定性系數(shù)降至最低，前峰型工況為1.02,中峰型降雨工況下為0.985。降雨結束后，滑面處的土體飽和度逐漸降低(圖9)，孔隙水壓力隨之不斷降低(圖10)，滑坡的穩(wěn)定性系數(shù)隨著模擬時間呈線性增大，模擬第七天時，ABA和BAA型降雨工況下滑坡的穩(wěn)定性系數(shù)分別增大至1.13和1.08。

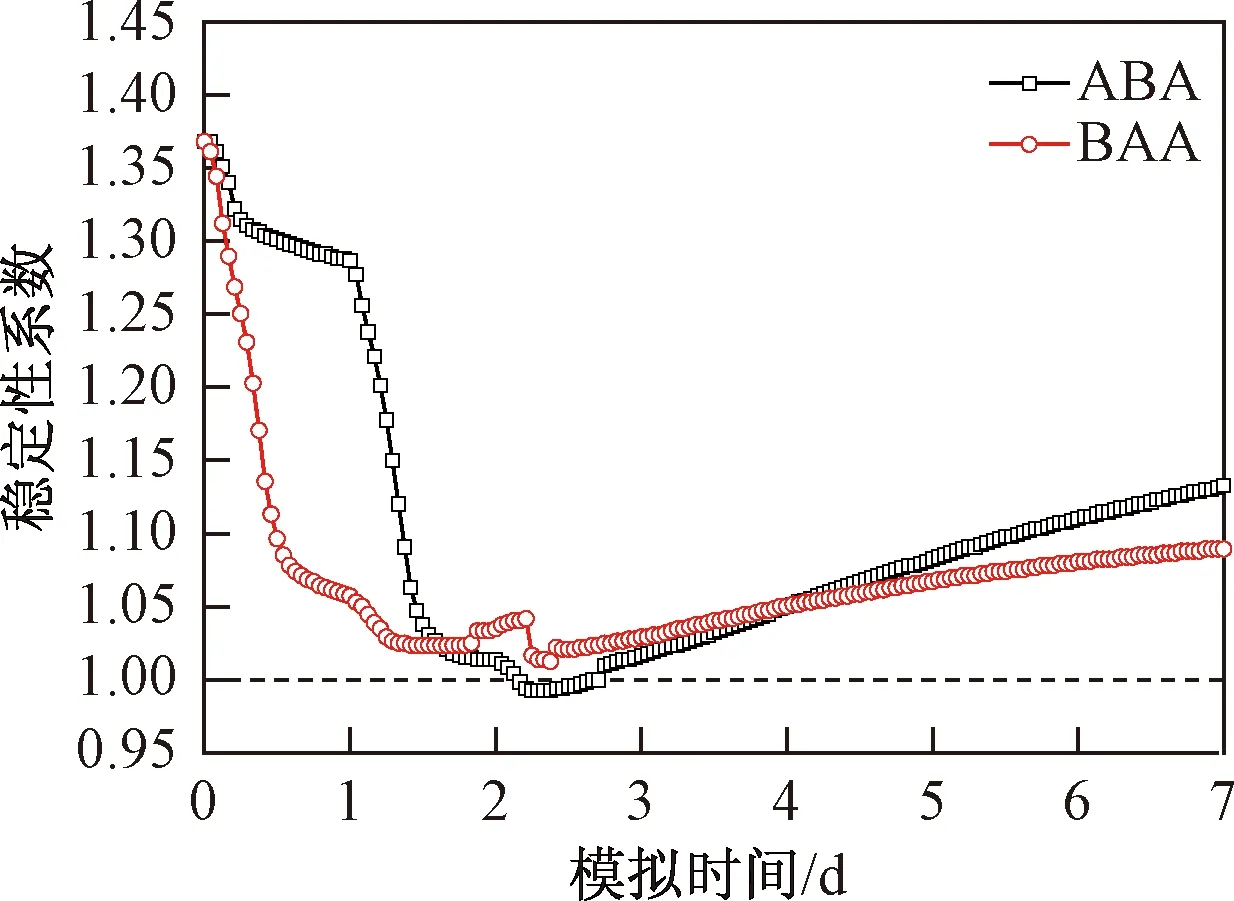
圖13 穩(wěn)定性系數(shù)變化Fig.13 Curves of the stability factor

通過土柱實驗及數(shù)值模擬的分析可知，在ABA和BAA兩種降雨工況下，10 mm/h降雨期間，玄武巖殘積土的雨水運移速率較小，土體的飽和度，孔隙水壓力增長速率較慢，而在峰值降雨期間，雨水運移速率可達10 mm/h期間的2～3倍，滑帶土迅速飽和，孔隙水壓力迅速增大，坡腳出現(xiàn)大面積的滯水，土體抗剪強度急劇降低。降雨第三天，滑坡的穩(wěn)定性系數(shù)降至最低，滑坡最終失穩(wěn)。比較ABA和BAA型降雨工況，前者的峰值降雨期間雨水運移速率更快，滑面土體的飽和度增長更快，坡腳處的局部滯水面積也更大，滑坡的穩(wěn)定性系數(shù)更小。因此，中峰降雨工況下，滑坡更容易失穩(wěn)。

5 結論

(1)降雨作用下，玄武巖殘積土土柱的淺層土體含水率增長速率較快，上部及深部土體更易達到飽和。

(2)10 mm/h降雨期間，玄武巖殘積土內(nèi)濕潤鋒下滲速率較小且不隨深度變化；30 mm/h降雨期間，濕潤鋒下滲速率可增大2～3倍，且隨深度的增加下滲速率逐漸減小，雨水主要通過峰值降雨期快速入滲。

(3)降雨作用下，馬濟頭滑坡的滑帶土迅速增大，孔隙水壓力隨之增大，坡腳出現(xiàn)大面積的滯水，土體抗剪強度急劇降低；模擬降雨第三天，滑坡的穩(wěn)定性系數(shù)降至最低，滑坡最終失穩(wěn)。

(4)中峰型降雨工況下雨水滲入滑坡體的速率更快，滑帶土的飽和度增長更快，坡腳處產(chǎn)生更大滯水面積滑坡更容易失穩(wěn)。