高壓除濕轉輪系統性能模擬與分析

嚴豪，葛天舒，代彥軍，王如竹

（上海交通大學制冷與低溫工程研究所，上海 200240）

0 引言

近年來，轉輪除濕憑借其結構簡單緊湊、運行效率高、除濕量大等優勢，逐步成為研究焦點，廣泛應用于生活和生產中。硅膠作為固體吸附材料具有無毒[1]、相對濕度適用范圍廣且吸附能力強[2]等特性，市場上的轉輪多以其為吸附材料進行制備[3]。

國內外關于除濕轉輪的數學模型研究較早。MACLAINE-CROSS等[4]使用比擬法分析了除濕轉輪的傳熱和傳質過程，利用對傳熱過程的求解來分 析預測傳質過程。BARBY等[5-6]將硅膠流床的傳熱系數和傳質系數實驗關聯式應用在HOUGEN等[7]提出的數學模型中，并通過實驗的方法研究了硅膠除濕轉輪的傳熱傳質過程。ZHENG等[8]使用隱式的有限差分法對轉輪的一維傳熱傳質過程進行模擬，并在此基礎上進行性能優化。DAI等[9]通過數值計算用參數分析法對除濕轉輪的性能進行了詳細地分析和討論。張學軍[10]通過對一個一維數學模型的數值計算，分析討論了運行參數、結構參數對轉輪除濕器性能的影響。NIU等[11]通過對一個二維數學模型的數值求解，討論了干燥劑厚度對除濕轉輪傳熱傳質的影響，指出在某一轉速下有一定厚度的活性層對于干燥劑而言是參加傳熱傳質活動的必要條件。MIHAJLO等[12]導出了分別適用于非冷凝條件和冷凝條件下的兩組控制方程。鐘金華[13]模擬研究了高壓下不同形狀因子對干燥劑吸附性能以及再生區冷凝情況的影響。

采用新型復合材料或者加大系統的工作壓力都是提高轉輪除濕效率的有效方法[14-15]，本文主要針對后者進行研究。除濕轉輪應用于壓縮空氣干燥時，運行工況由大氣壓力變為高壓，固體干燥劑的吸附和解吸能力將發生改變，在高壓工作環境下，轉輪的吸附能力得到提升，但同時，再生區域有可能發生凝結現象，降低干燥劑的解吸能力，使除濕效果變差。本文對高壓工作環境下轉輪的傳熱傳質過程建立了控制方程，并利用數值方法進行模擬分析，討論了工作壓力下各參數對轉輪干燥效率（以除濕量和壓力下露點為考察標準）的影響，為除濕轉輪在壓縮空氣領域的應用提供理論基礎。

1 空壓機深度除濕循環

圖1所示為高壓除濕轉輪系統循環。整個轉輪處在高壓環境下，從空壓機出來的氣體分離成兩股：其中15%的壓縮氣體作為再生熱空氣，進入轉鼓干燥機再生區，然后通過冷卻器；剩余的85%壓縮空氣經過冷卻降溫后，與解吸后的再生空氣匯總，隨后進入轉鼓干燥機進行吸附處理，最終排出，以達到整個裝置零氣耗的效果。

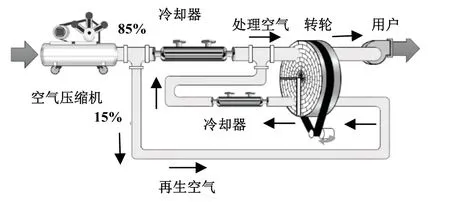
圖1 高壓除濕轉輪系統循環

圖2所示為轉輪系統。除濕轉輪是整個系統的核心，一般由涂有吸附材料（硅膠、分子篩等）的基材料（紙基或陶瓷基）組成，負責對高壓空氣的除濕處理。轉輪兩側由特殊的密封裝置分成兩個區域：處理區域和再生區域。處理區域中，干燥材料吸附氣體中的水分進行除濕；再生區域中，高溫空氣帶走干燥材料中水分對其進行再生。轉輪不斷轉動，以保證除濕系統持續穩定的除濕狀態。

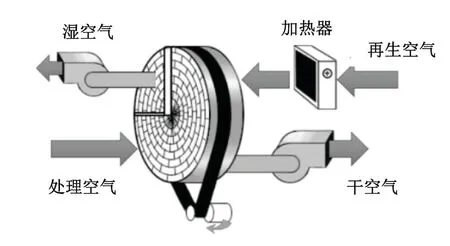
圖2 轉輪系統

2 系統模型構建

由于本文所研究的是承壓工況下的轉輪除濕性能，在高壓條件下，再生區域的干燥材料可能出現不能完全解吸的情況，此時再生區域會發生冷凝。本文將根據是否發生冷凝來建立模型并進行調節。

2.1 沒有冷凝發生時的系統模型

當沒有冷凝發生時，系統的控制方程與常壓下的相似[16]，對常壓下的轉輪系統進行模擬。將除濕轉輪按照31∶的比例劃分為處理區和再生區，并以轉輪截面中心為起點，螺旋向外做波紋形通道[17-20]，如圖3所示。選取除濕轉輪中的某一個氣流通道，建立拉格朗日坐標系，在dz內可以采用集總參數法，建立一維傳熱傳質數學模型進行數值求解，如圖4所示。

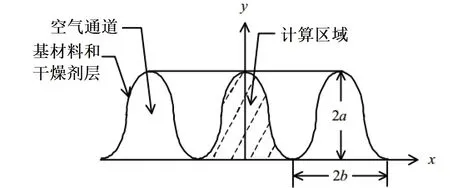
圖3 波紋型通道

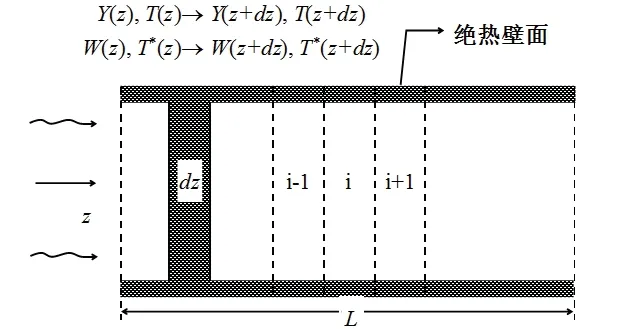
圖4 波紋形空氣通道內部微元體

沒有冷凝發生時，根據質量和能量守恒定律，建立控制方程，并寫成時間導數和空間導數向后差分的隱式迎風差分方程[10]，對上述方程采用全主元高斯-約當消元法，通過計算機編程求解[21]。

2.2 冷凝發生時的判定條件與模型調整

采用安東尼飽和水蒸汽壓方程判斷是否發生冷凝[22]。

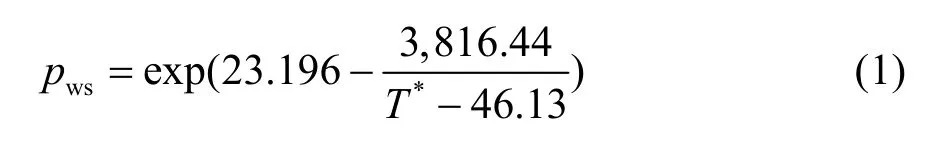
式中：

T*——干燥劑溫度，℃；

pw——水蒸氣分壓力，MPa。

當pw＞pws時，冷凝發生。冷凝發生時，控制方程將進行轉變[13]。

2.3 模擬所用的初始工況

假設承壓狀態下硅膠的吸附率提升30%，模擬計算所采用的參考工況參數條件如表1所示。

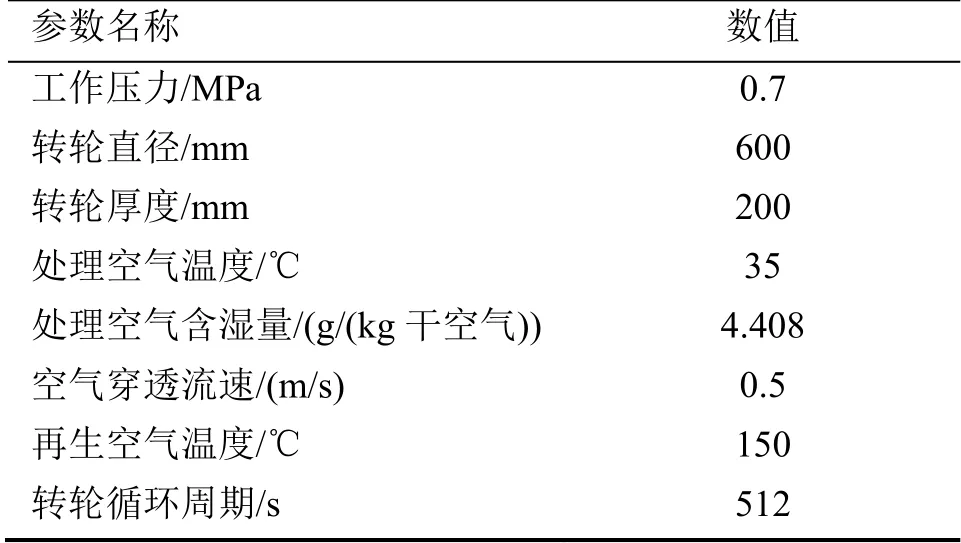
表1 數值計算所采用參數

2.4 承壓下空氣參數的變化

與常壓對比，在承壓狀態下，空氣側的物性參數將發生變化。查詢0.7 MPa壓力下空氣側發生變化的參數，如表2所示。

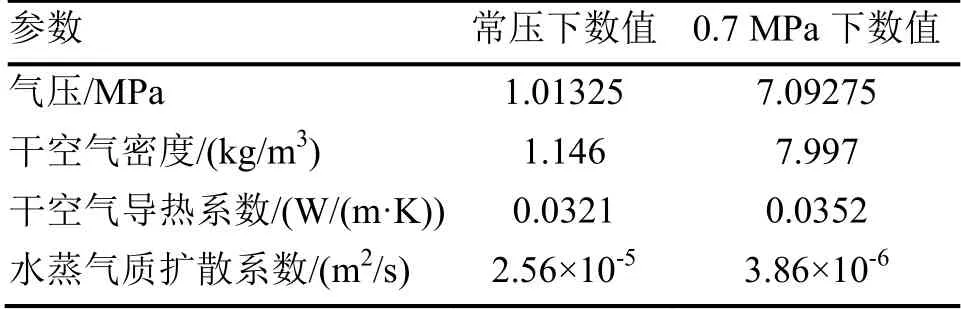
表2 0.7 MPa壓力下相對常壓的變化參數

3 模擬結果分析

本文采用除濕量D來描述轉輪的除濕性能：

式中：

Yp1、Yp2——處理空氣的進出口含濕量， g/(kg干空氣)。

除濕量D體現了處理空氣經過轉輪之后，絕對含濕量的變化。D越大，說明轉輪的除濕能力越強。

根據建立的數學模型，通過控制變量法改變參數，模擬計算出轉輪的除濕量D及0.7 MPa壓力下出口處露點溫度，并據此評判轉輪系統的除濕性能。

3.1 再生溫度對系統除濕性能的影響

圖5給出了其他參數不變時，再生溫度從120 ℃到180 ℃，對轉輪系統除濕性能的影響。從模擬結果可以看出，隨著再生溫度的提高，轉輪的除濕量D上升，出口處的空氣露點溫度逐漸降低，降低幅度呈減緩趨勢。再生溫度越高，除濕轉輪的解吸速率就越快，因此系統的除濕量上升。

圖5 再生溫度對系統除濕性能的影響

3.2 停留時間對系統除濕性能的影響

停留時間的定義如式（3）所示：

式中：

L——轉輪軸向厚度，m；

v——空氣流速，m/s。

固定軸向空氣流速為0.5 m/s不變，通過改變轉輪厚度來控制空氣在轉輪內部停留的時間長短。圖6所示為停留時間對系統除濕性能的影響，空氣在轉輪內停留時間越長，吸附越充分，露點溫度越低，但當厚度到達到一定值時，由于空氣干燥得足夠充分，繼續加厚所帶來的除濕量提升逐漸趨于零。

固定轉輪厚度為200 mm不變，改變軸向空氣穿透速度，并分析其對轉輪系統的除濕性能的影響。如圖7所示，隨著穿透速度的不斷提高，處理氣體在轉輪中停留的時間越來越短，除濕效果越來越弱。但是，降低流速到達一定程度后，對除濕效果的提升不明顯，并且過低的流速可能導致轉輪系統不滿足流量的要求，因此適當降低流速可以提高轉輪的除濕性能。

圖6 固定流速時停留時間對系統除濕性能的影響

圖7 固定厚度時停留時間對系統除濕性能的影響

3.3 吸附時間對系統除濕性能的影響

吸附時間是指轉輪吸附區初始的一個微元轉過整個吸附區所需的時間，占轉輪轉動周期的四分之三，與轉速有直接關系。

改變吸附時間對系統除濕性能的影響如圖8所示，圖中給出了出口端空氣的露點溫度與吸附時間的關系。可以發現，除濕轉輪存在一個最優轉速使系統能獲得最大的除濕量。露點溫度隨著吸附時間的升高呈先下降后上升的趨勢，在150 s左右存在一個最優值使除濕量最大，表明在此條件下的最優周期為200 s，即18 r/h的轉速有利于提高轉輪的吸附性。

3.4 轉輪直徑對系統除濕性能的影響

轉輪直徑也是系統除濕效率的因素之一。提升轉輪的直徑可以讓入口空氣的接觸面積增大，使除濕效果更好，但同時要考慮經濟和空間的限制。圖9所示為轉輪直徑對系統除濕性能的影響，隨著轉輪直徑的增加，按比例提高單位長度基材料和干燥劑的質量。可以看出，隨著轉輪直徑的增加，系統除濕量D逐漸上升，出口氣體的露點溫度呈現下降趨勢，并且這種趨勢在800 mm之后有所減緩。

圖8 吸附時間對系統除濕性能的影響

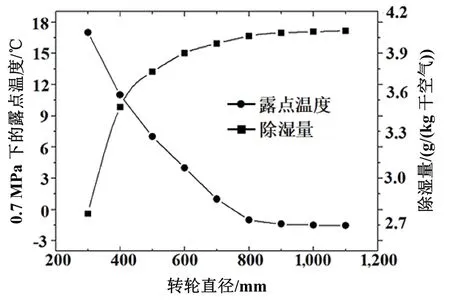
圖9 轉輪直徑對系統除濕性能的影響

3.5 優化參數選取

通過上述比較分析，對轉輪參數的優化選取如表3所示。

表3 轉輪優化參數選擇

4 結論

本文建立了高壓下轉輪除濕系統的數學模型，并通過模型模擬計算，分析了各種參數對轉輪系統除濕性能的影響，得出如下結論：

1）適當提高再生溫度能夠提升轉輪的除濕性能；

2）加大空氣在轉輪中的停留時間有利于提高系統除濕性能；

3）存在最優轉速，使轉輪的除濕效果最好；

4）在空間和經濟條件允許下，適當加大轉輪截面積也能提升轉輪的干燥性能；

5）以表3所示參數進行模擬，最終出口處可以達到0.7 MPa壓力下露點溫度為-5 ℃。

本文模擬分析了各參數對承壓狀態下轉輪除濕性能的影響，并對參數進行優化選取，為今后承壓除濕轉輪實驗臺的建立以及除濕轉輪在壓縮空氣領域的應用提供了初步的理論基礎。