高速鐵路簡支箱梁日照溫差的變化規律

張 欣，劉 勇

(湖南省交通規劃勘察設計院有限公司，湖南 長沙 410219)

我國高速鐵路大量采用高架橋方案，橋梁占線路里程的比例超過50%，而標準跨徑預應力混凝土整孔簡支箱梁占橋梁總里程的比例超過90%[1]。混凝土材料傳熱性能差，箱梁的溫度傳遞具有明顯的時滯效應。日照作用下橋梁結構中會產生溫度應力，導致混凝土結構損傷和開裂。控制箱梁內部溫差對確保結構的安全性和耐久性具有重要意義。Kehlbeck[2]采用一維瞬態熱傳導理論分析混凝土橋梁的溫度應力和變形，將日照溫度環境分為太陽直接輻射、天空輻射、大氣逆輻射、周圍環境輻射等；劉興法[3]通過對箱梁結構溫度實測數據進行擬合，指出溫差曲線為負指數函數，并基于彈性假定計算了箱梁的縱橫向溫度應力；鐵四院科研所[4]對長沙水塔溫度分布進行現場實測，給出了圓形空心高墩徑向和環向溫度的分布規律。

目前，混凝土橋梁結構日照溫差分布的研究方法多基于特定橋梁溫度實測數據的數理統計[5-11]，基于通用有限元軟件分析混凝土橋梁結構的日照溫差分布的研究相對較少。本文探討箱梁與外界環境的熱交換機理，建立考慮時變熱流邊界的箱梁日照溫度場參數化有限元模型，采用時變非線性熱力學分析方法，計算箱梁的日照溫度場分布，并采用實測數據進行驗證。以我國高速鐵路無砟軌道32 m簡支梁橋為例，研究客運專線標準跨徑簡支箱梁日照溫差分布特征，通過對計算參數的比較分析，提出控制箱梁溫差的建議。

1 箱梁時變溫度場計算模型

混凝土箱梁作為縱向狹長結構，可忽略其溫度場沿縱向的變化，采用截面溫度場代表結構的溫度場。成橋狀態日照作用下，混凝土橋梁結構的時變溫度場由導熱基本方程表示[12]，即

(1)

式中：T為橋梁結構絕對溫度；τ為時間；a為導溫系數，a=λ/(ρc)；λ為導熱系數；ρ為混凝土密度;c為混凝土比熱容。

導熱微分方程的定解條件包括初始條件和邊界條件兩方面。

1.1 初始條件

時變溫度場分析過程中，近似地給定溫度分布較為明確的特定時刻結構內部溫度場，再基于該初始值進行瞬態分析。為消除初始條件對計算結果的影響，需要經過一個渡越時間的計算，使其影響逐漸減弱直至可以忽略。通過合理選取箱梁初始溫度場，可明顯提高算法的穩定性[11]。

1.2 邊界條件

混凝土箱梁受太陽短波輻射，與環境存在熱對流和長波輻射換熱。其溫度邊界條件同時包含第二、三類邊界條件，求解溫度場時應將兩類溫度邊界條件進行組合。為便于計算，將各類邊界條件以熱流形式進行統一，則邊界凈流入熱流密度為

(2)

到達橋梁結構任意表面的太陽短波輻射可根據路徑不同分為太陽直接輻射Iθ、地表反射If和大氣散射Iβ三部分，故箱梁的太陽短波輻射總熱流密度qz為

qz=at(Iθ+Iβ+If)

(3)

式中，at為混凝土短波輻射吸收率。

橋梁結構接收的短波輻射來源于太陽光，該項輻射的有無由日出日落狀態決定。

混凝土橋梁在風作用下受到大氣的強制對流，橋梁外表面的強制對流換熱遵循牛頓冷卻定律，即

qc=h(Ta+T)

(4)

式中：qc為對流總熱流密度；Ta為大氣溫度。

箱梁的輻射熱交換包含吸收外界輻射和向外輻射能量兩部分，外界輻射來源主要有大氣輻射Gaβ和地表輻射Uaβ。設向外輻射的能量為El，則混凝土的輻射熱交換總熱流密度qr可以表示為

qr=al(Gaβ+Uaβ)-El

(5)

式中，al為混凝土長波輻射吸收率。

1.3 計算流程

混凝土箱梁日照溫度場仿真分析的流程如下：

1)確定并輸入橋梁所處的地理位置及方位角、計算日期及對應的氣溫等計算參數；

2)基于ANSYS建立箱梁溫度場計算幾何模型，并選取Plane55單元對溫度場模型進行單元劃分；

3)假定箱梁初始溫度場，并考慮短波輻射、對流換熱和輻射換熱對箱梁熱流邊界的影響。針對箱梁不同方向的邊界，將時變熱流邊界分別存入以時間、溫度和位置坐標為索引值的多維數據表格中；

4)基于假定的初始溫度場，采用ANSYS中的表格加載功能，根據計算的時間、溫度和坐標值，對熱流進行加載。以0.5 h為步長，分步計算箱梁溫度。

2 箱梁溫差分析與驗證

2.1 工程背景

我國高速鐵路無砟軌道客運專線橋梁普遍采用32 m簡支梁橋形式，配以24 m簡支梁調跨。為保證外觀協調一致，調跨梁高與32 m簡支箱梁相同，斷面形式也相同。

選取合福客運專線上饒段某跨移動模架現澆施工的32 m簡支梁為例，計算其在日照作用下的溫差。橋址位于東經117.97°，北緯28.45°，橋梁方位角6.92°。選取連續天氣晴好的2013年12月27日至2014年1月2日進行分析，其最值氣溫曲線見圖1。混凝土箱梁溫度場的計算參數見表1。

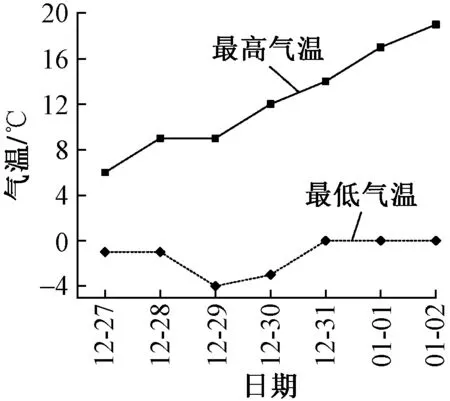
圖1 最值氣溫曲線

計算參數取值混凝土導熱系數/[kJ·(h·K·m)-1]10.8空氣導熱系數/[kJ·(h·K·m)-1]0.086 4混凝土短波輻射吸收率0.60地表短波反射率0.18混凝土長波輻射吸收率0.85大氣透明度系數0.80

2.2 箱梁溫差特性研究

為減小初始假定溫度場的影響，選取第6 d典型時刻箱梁的頂、底板豎向及腹板水平溫度梯度進行分析。以頂板下緣為參考對象，箱梁頂板豎向溫差見圖2。

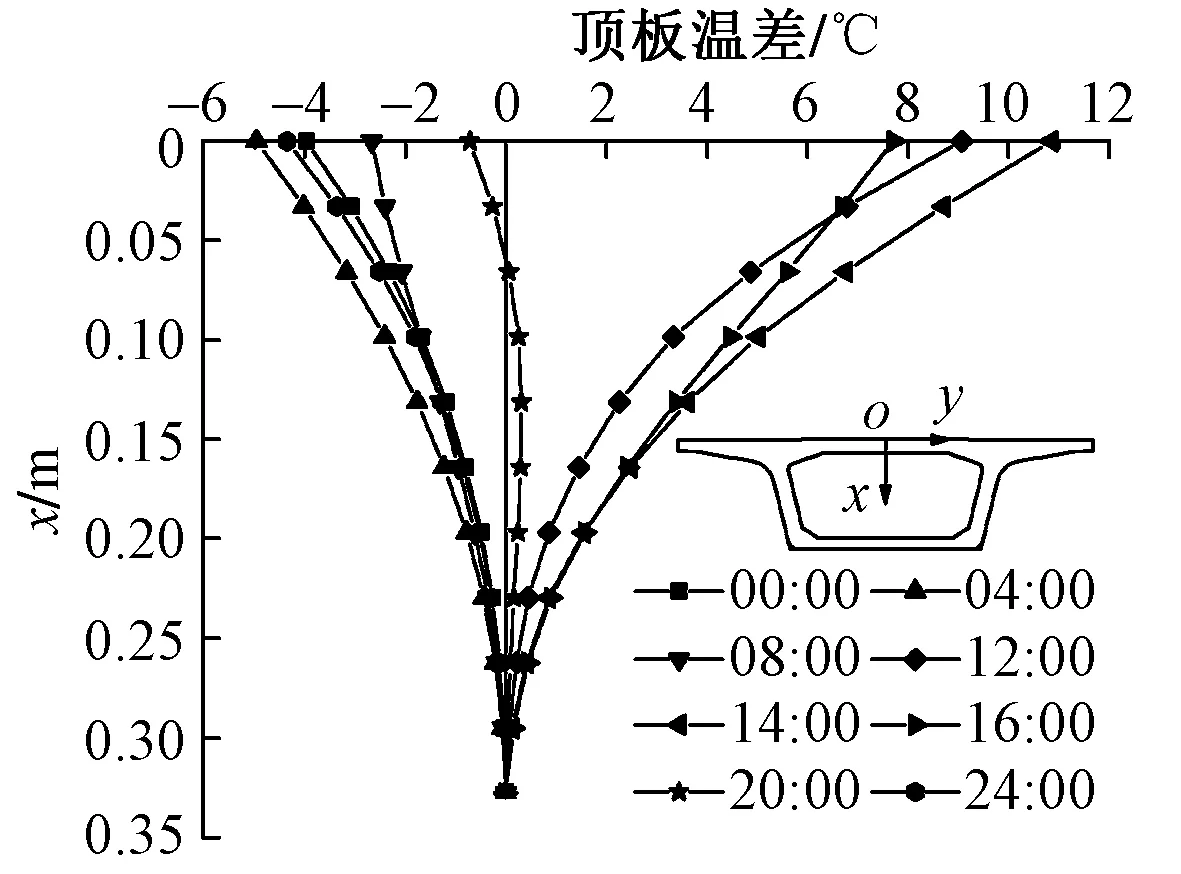
圖2 箱梁頂板豎向溫差

由圖2可知：①箱梁頂板內存在較大的豎向溫差，且隨時間的變化而不同；②最大正溫差達10.9 ℃，出現在14:00左右；③最大負溫差達-5.0 ℃，出現在04:00 左右；④08:00和20:00時頂板內的豎向溫差較小，溫度分布較均勻。設箱梁溫差為ΔTb,則箱梁頂板最大正溫差曲線可擬合為ΔTb=12.30e-7.17x-1.42，最大負溫差曲線可擬合為ΔTb=-5.89e-6.20x+0.90，表明箱梁頂板正、負溫差均呈負指數分布且外緣溫度變化較快而內緣變化較緩；正溫差函數負指數系數大于負溫差函數指數系數，表明正溫差曲線相對于負溫差曲線變化更迅速。原因是箱梁頂板正溫差是由日照輻射引起的溫差和氣溫變化引起的溫差組成，而負溫差則是夜間氣溫降低導致，故頂板的最大正溫差在數值上明顯大于最大負溫差。

以底板上緣為參考對象，箱梁底板豎向溫差見圖3。

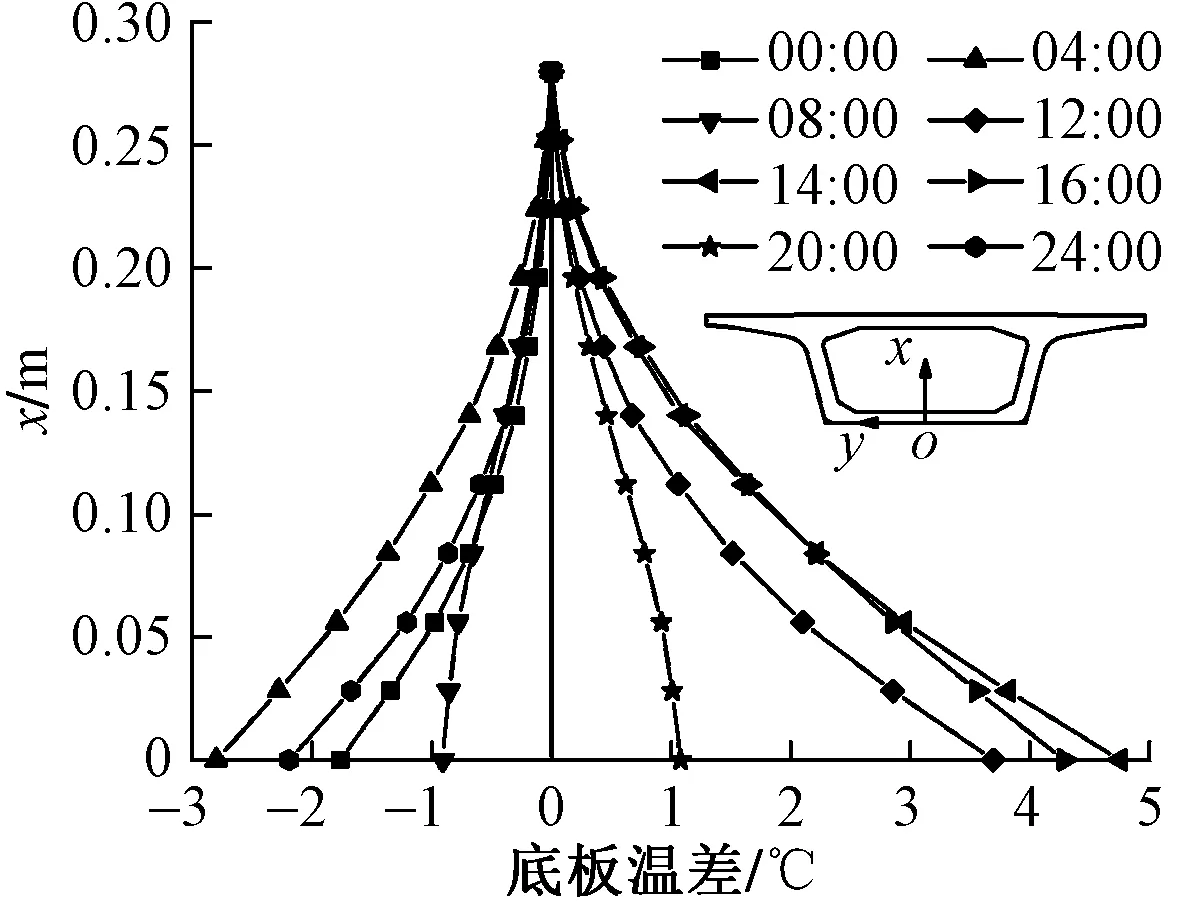
圖3 箱梁底板豎向溫差

由圖3可知：①箱梁底板內豎向溫差較大，且隨時間的變化而不同；②最大正溫差達4.8 ℃，出現在14:00 左右；③最大負溫差達-2.8 ℃，出現在04:00左右；④08:00 和20:00時底板內的豎向溫差較小，溫度分布較均勻。箱梁底板最大正溫差曲線可擬合為ΔTb=5.62e-7.30x-0.85，最大負溫差曲線可擬合為ΔTb=-3.31e-7.31x+0.50。箱梁底板正、負溫差指數系數基本相同，表明該處溫度變化主要由前項系數決定。

以腹板內緣為參考對象，箱梁腹板溫差見圖4。

圖4 箱梁腹板溫差

由圖4可知：①箱梁腹板內水平溫差較大，且隨時間的變化而不同；②最大正溫差達5.5 ℃，出現在16:00 左右；③最大負溫差達-3.2 ℃，出現在04:00左右；④24:00時腹板內的溫差較小。箱梁腹板最大正溫差曲線可擬合為ΔTb=6.37e-5.48x-0.63，最大負溫差曲線可擬合為ΔTb=-3.30e-5.92x+0.29。

2.3 箱梁溫差實測驗證

為驗證箱梁溫差有限元計算結果的可靠性，在32 m 簡支梁梁體中預埋溫度傳感器，對箱梁的溫度場進行連續觀測。在箱梁頂板、底板和腹板中距上下緣或內外緣5 cm處預埋溫度測量元件，利用分布式網絡測量系統對箱梁內各測點的溫度進行實時采集，并通過網絡發送至數據處理終端，采樣間隔時間為30 min。箱梁跨中溫度測點布置如圖5所示。

圖5 溫度測點布置示意(單位：cm)

提取各測點溫差并與實測值進行對比。限于篇幅，本文僅選取具有代表性的1個周期進行對比，見表2。

表2 箱梁內外測點溫差對比 ℃

由表2可知：①有限元計算值與現場實測值符號相同，大小基本一致，且具有一致的變化趨勢；②由于測點位置偏差、豎向普通鋼筋的影響、橋位氣溫與氣象資料存在偏差等原因，有限元計算值與現場實測值存在一定差異，頂板、底板及腹板內的最大溫差僅相差0.3 ℃，0.7 ℃和0.2 ℃，其相對誤差分別為3.8%，20%和4.8%。說明基于ANSYS的箱梁溫度場有限元模型能較好地模擬箱梁的邊界條件和實際溫差，計算結果滿足工程結構分析的精度要求。

3 計算參數影響分析

影響日照作用下箱梁溫差分布的主要因素包括大氣透明度系數、混凝土短波輻射吸收率、晝夜溫差、覆蓋層厚度等。

3.1 大氣透明度系數

大氣透明度系數p決定了太陽光在橋位處的輻射強度，透明度系數越高太陽輻射強度越大。針對不同的大氣透明度系數，繪制箱梁頂板溫差隨時間的變化曲線，見圖6。

圖6 不同大氣透明度系數下箱梁頂板溫差隨時間的變化曲線

由圖6可知：隨著大氣透明度系數提高，箱梁頂板內的最大正溫差和最大負溫差均有所增大，溫差大小與大氣透明度系數存在二次函數關系。最大正溫差曲線為Tmax=3.99p2+2.99p+5.75，最大負溫差曲線為Tmin=-3.33p2+1.27p-3.80。大氣透明度系數越高，頂板內溫差隨大氣透明度系數的變化越明顯。

箱梁底板及腹板溫差隨大氣透明度系數的變化見表3。

表3 箱梁底板及腹板溫差隨大氣透明度系數的變化 ℃

由表3可知：①底板正、負溫差絕對值均隨大氣透明度系數的增加而略有增大，增幅分別為0.49，0.20 ℃。②腹板正溫差隨大氣透明度系數的增加而減小，降幅可達0.61 ℃，原因是此處箱內氣溫上升速率大于箱外氣溫；負溫差隨大氣透明度系數的增加而增大，增幅可達0.46 ℃。說明從減小箱梁溫差的角度考慮，降低大氣透明度系數對減小頂板和底板的正、負溫差及腹板的負溫差均有利，而對腹板正溫差不利。

3.2 混凝土短波輻射吸收率

形成箱梁溫差的根本原因在于梁體表面存在時刻變化的熱流邊界，而混凝土的熱傳遞具有明顯的時滯性。混凝土短波輻射吸收率決定了結構在受到太陽輻射作用時能被結構吸收的輻射量，故混凝土短波輻射吸收率是箱梁溫差分布的重要影響因素。

不同混凝土短波輻射吸收率條件下箱梁溫差研究表明：混凝土短波輻射吸收率對頂板正、負溫差影響較為明顯，成正相關關系，其關系式分別為Tmax=11.97at+3.58和Tmin=-4.16at-2.43。混凝土短波輻射吸收率每降低0.1，頂板正溫差減小約1.20 ℃，負溫差減小約0.42 ℃。

箱梁底板和腹板溫差隨混凝土短波輻射吸收率的降低而略有減小，混凝土短波輻射吸收率每降低0.1，其溫差降幅均在0.17 ℃范圍內。為有效降低箱梁溫差，可僅對頂板混凝土表面進行處理，如涂刷淺色涂料、提高混凝土表面光潔度等。

3.3 晝夜氣溫差

對于晴好天氣，大氣溫度在一天內的變化基本符合正弦曲線規律，其數值由日最高和日最低氣溫決定。橋梁結構處于大氣環境中，其溫度場及溫差分布受大氣溫度的影響。箱梁溫差隨晝夜氣溫差ΔT的變化見圖7。

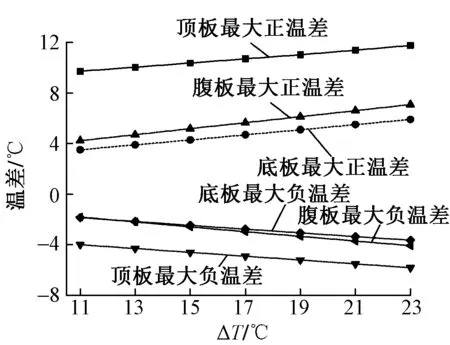
圖7 箱梁溫差隨晝夜氣溫差的變化

由圖7可知：①箱梁各部位的最大正、負溫差均與晝夜氣溫差成正相關關系，頂板正、負溫差均遠大于腹板和底板的溫差，腹板溫差略大于底板溫差。②隨著晝夜氣溫差的增大，頂板、底板和腹板的最大正溫差均呈線性遞增的趨勢，其變化率分別為0.17，0.20，0.24。③各部位的最大負溫差隨晝夜氣溫差的增大而增大，頂板、底板和腹板的負溫差變化率分別為-0.16，-0.15和-0.19。

3.4 覆蓋層厚度

研究表明，混凝土箱梁頂板溫差最大，且溫差沿厚度方向呈負指數分布；混凝土表面的溫度變幅最大，并在較小厚度范圍內迅速降低。針對頂板設置了不同厚度的非受力覆蓋層，箱梁頂板溫差隨覆蓋層厚度H的變化見圖8。可知，箱梁頂板溫差隨覆蓋層厚度增大而減小，且溫差曲線有整體向后推遲的趨勢。

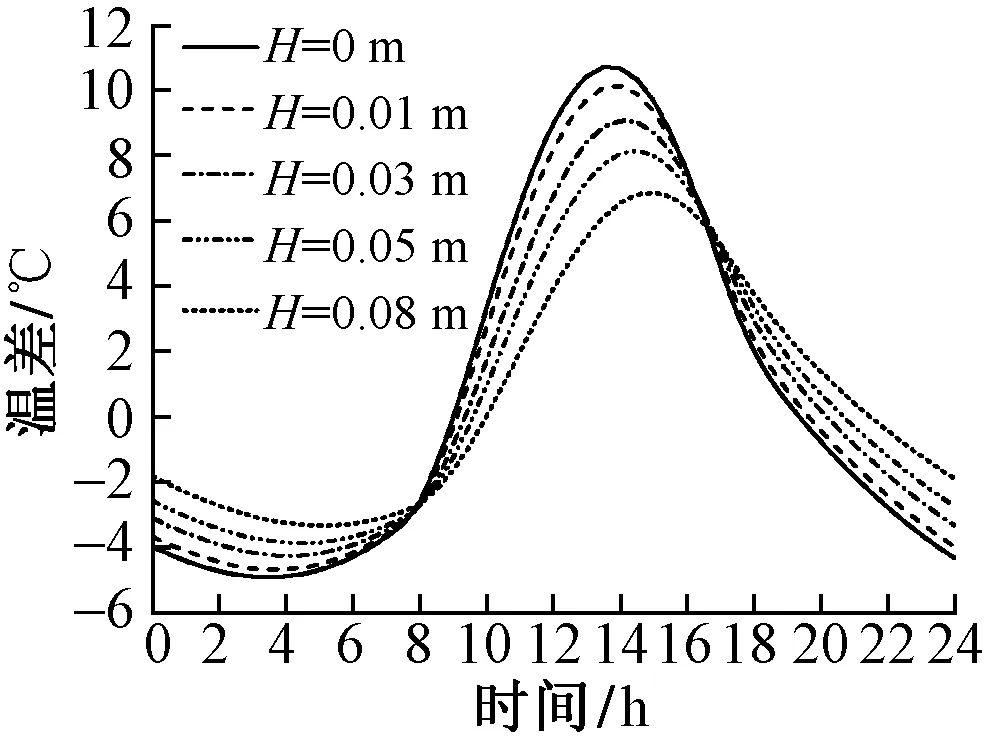
圖8 箱梁頂板溫差隨覆蓋層厚度的變化

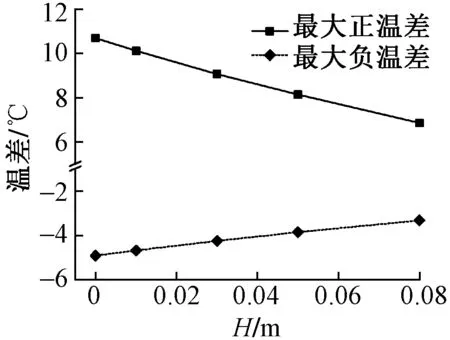
圖9 箱梁頂板溫差最值隨覆蓋層厚度的變化

箱梁頂板溫差最值隨覆蓋層厚度的變化見圖9。可知：頂板最大正、負溫差隨覆蓋層厚度變化規律可分別表示為Tmax=-47.82H+10.61和Tmin=19.75H-4.88。隨著覆蓋層厚度的增加，正溫差降低0.48 ℃/cm，負溫差降低0.20 ℃/cm。最大正、負溫差的出現時刻分別為tmax=15.13H+13.69和tmin=19.87H+3.47。無覆蓋層時最大正、負溫差出現的時刻分別為13:41和03:28，有覆蓋層時最大正、負溫差出現時刻分別延遲0.15 h/cm 和0.20 h/cm。

4 結論

1)箱梁內各部位的最大正、負溫差均以外表面為起點沿厚度方向呈負指數分布，且最大正溫差在數值上大于負溫差。

2)箱梁溫差最大值與大氣透明度系數成二次函數關系，隨著大氣透明度系數的提高，箱梁頂板和底板的正、負溫差及腹板的負溫差增大，而腹板正溫差隨之減小。

3)箱梁溫差與混凝土短波輻射吸收率成正相關關系。可對混凝土表面進行處理，如涂刷淺色涂料、提高混凝土表面光潔度等，能有效減小箱梁溫差。

4)晝夜氣溫差對箱梁溫差分布的影響顯著，晝夜氣溫差越大，箱梁各部位的日照溫差越大。

5)增大梁頂非受力覆蓋層厚度可使箱梁頂板的溫差隨之線性降低，且最大正、負溫差出現時間將向后推遲。