基于分數階微分算子與高斯曲率相結合的自適應圖像去噪

周先春 張敏 吳婷

摘 要： 文中提出分數階微分算子和高斯曲率相結合的自適應圖像去噪方法。將高斯曲率引入偏微分方程模型中，由圖像梯度進行邊緣檢測，再結合高斯曲率和分數階微分算子的性質，由圖像的局部方差建立分數階微分算子，構建基于分數階微分算子的自適應圖像去噪模型，進行自適應地擴散去噪。結果表明，新算法性能優異，內部信息保護更具完整性，有利于實際應用。

關鍵詞： 圖像去噪; 邊緣檢測; 去噪模型; 自適應擴散去噪; 高斯曲率; 分數階微分算子

中圖分類號： TN911.7?34; TP391.41 ? ? ? ? ? ? ? ? ?文獻標識碼： A ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2019）15?0054?05

Adaptive image denoising based on fractional differential operator and Gauss curvature

ZHOU Xianchun， ZHANG Min， WU Ting

（School of Electronic and Information Engineering， Nanjing University of Information Science and Technology， Nanjing 210044， China）

Abstract： An adaptive image denoising method combining Gauss curvature with fractional differential operator is proposed in this paper. The Gauss curvature is introduced into the partial differential equation model， and the image edge is detected by the image gradient. In combination with the properties of the Gauss curvature and fractional differential operator， the fractional differential operator is established by means of the local variance of the image. An adaptive image denoising model based on fractional differential operator is constructed to carry out adaptive diffusion denoising. The results show that the new algorithm has better performance and can protect internal information more entirely， which is beneficial to practical application.

Keywords： image denoising; edge detection; denoising model; adaptive diffusion denoising; Gauss curvature; fractional differential operator

0 ?引 ?言

圖像降噪算法因為其實際的作用和廣泛的需要，受到國內外學者的關注和研究[1?3]。其中，降噪在基于偏微分方程模型和變分模型兩個方面的研究，許多學者做了相應的工作[4?10]。

本文結合圖像的幾何屬性，將高斯曲率引入偏微分方程中，研究中獲得在增強信號高頻分量時，分數階微分算子作用明顯，且能有效削弱信號的中頻和低頻部分，從而進一步結合高斯曲率和分數階微分算子建立新的去噪模型，自適應地進行邊緣檢測，內部信息保護更具完整性，有利于實際應用。

1 ?PM模型和TV模型

20世紀90年代，Perona和Malik首先提出能夠保持邊界的各向異性熱擴散方程，被稱為PM模型。

其中，該模型調整擴散的力度是依據梯度的大小來調整。[?I>k]，有[g?I→0]，即擴散在邊緣停止;[?I

2 ?基于分數階微分算子的自適應圖像去噪

3 ?新模型的加性算子分裂數值算法

4 ?實驗結果與分析

用峰值信噪比（PSNR）和結構相似度（SSIM）評價新模型和已有模型的去噪性能，分別對Barbara[512×512]和Buddha[512×512]圖像加隨機高斯噪聲（方差為20）進行實驗，原始圖像如圖1所示。

圖1 ?原始圖像

現分別與維納濾波器、小波去噪（小波硬閾值算法、小波軟閾值算法）、正則化PM模型、ROF模型和新模型對圖像進行平滑去噪。這里，[Δt=5]，迭代次數等于7，均值和維納濾波器的窗口為[3×3]，PM模型取式[g?I=11+?Ik2]，閾值為10;ROF模型的[λ=0.02];去噪效果見圖2，Barbara局部放大見圖3，新模型與已有模型的邊緣檢測結果見圖4。

圖2 ?各模型平滑后的Barbara圖像

圖3 ?各模型平滑后局部放大的Barbara圖像

再對Buddha圖像進行實驗分析，模型比較和參數設置同Barbara。去噪效果見圖5，Buddha局部放大見圖6，新模型與已有模型的邊緣檢測結果見圖7， 表1為評價指標。

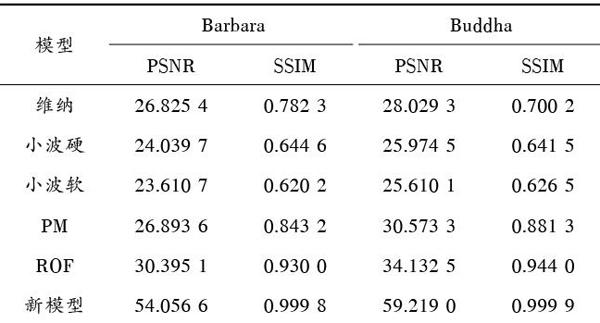
從圖2d）和圖5d）的整體結果圖可知，傳統的空域濾波器去噪效果很不好，這是由空域濾波器的本身局限性決定的。從圖3c）和d）、圖4c）和d）、圖7c）和d）可以看出，WHT方法和WST方法濾波效果不太理想，雖然該方法能夠較好地估計噪聲方差，并去除圖像中的噪聲，但會將圖像高頻子帶中的小波系數誤認為噪聲系數而去除，產生了圖像的階梯效應現象。從圖2e）和f）及圖5e）和f）的整體去噪結果可知， PM模型和TV模型雖然有一定的平滑作用， 但清晰度不高，主要原因還是在于二者的邊緣檢測均采用梯度，處理噪聲干擾效果不佳，這從圖4e）和f）及圖7e）和f）的邊緣提取效果圖中的角點、尖峰、窄邊緣和紋理等較為模糊，亦可得到驗證。由圖2g），圖4g），圖5g），圖7g）和表1指標可知，本文提出的新方法有效地控制圖像邊緣紋理細節信息，去噪后圖像的PSNR和SSIM有了大幅度提升，其內部信息結構保護更具完整性，去噪性能也更具理想化。

圖4 ?各模型平滑后邊緣提取的Barbara圖像

圖5 ?各模型平滑后的Buddha圖像

圖6 ?各模型平滑后局部放大的Buddha圖像

圖7 ?各模型平滑后邊緣提取的Buddha圖像

表1 ?各圖像使用不同去噪模型的PSNR與SSIM指標的比較

為進一步檢測本文提出的新方法的性能，在不同噪聲方差的條件下，用PSNR和SSIM對去噪結果進行性能分析，由圖8和圖9可知，本文提出的新模型在所有模型中PSNR最好，SSIM最好，可視性也最好，不僅有效去除了噪聲的干擾，而且對于圖像邊緣結構信息有了一定的增強，從局部穩定控制圖像信息進一步證實了新模型良好的去噪性能。

圖8 ?各模型不同方差下的峰值信噪比

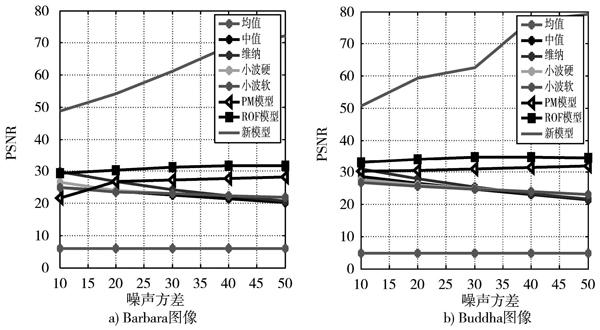
圖9 ?各模型不同方差下的結構相似度

5 ?結 ?論

本文提出基于分數階微分算子的自適應圖像去噪模型，先結合圖像梯度進行邊緣檢測，再結合高斯曲率和分數階微分算子的性質，由圖像的局部方差建立分數階微分算子，新模型有效地控制了圖像邊緣紋理細節信息，去噪后圖像的PSNR和SSIM有了大幅度提升，其內部信息結構保護更具完整性，去噪性能也更具理想化，具有一定的先進性和實用性。

參考文獻

[1] 李鵬，鄒楊，姚正安.四階各向異性擴散方程在圖像放大中的應用[J].中國圖象圖形學報，2013，18（10）：1261?1269.

LI P， ZOU Y， YAO Z A. Fourth?order anisotropic diffusion equations for image zooming [J]. Journal of image and graphics， 2013， 18（10）： 1261?1269.

[2] LI Zhongbin， LIU Zhizhao， SHI Wenzhong. A fast level set algorithm for building roof recognition from high spatial resolution panchromatic images [J]. IEEE geosci remote sens， 2014， 11（4）： 743?747.

[3] WANG Z， HUANG X， LI Y X， et al. A new image encryption algorithm based on the fractional?order hyperchaotic Lorenz system [J]. Chinese physics B， 2013，22（1）： 124?130.

[4] 周先春，汪美玲，周林鋒.擬正態分布擴散的圖像平滑[J].中國圖象圖形學報，2015，20（2）：169?176.

ZHOU X C，WANG M L，ZHOU L F. Image smoothing algorithm based on matching normal distribution diffusion [J]. Journal of image and graphics， 2015， 20（2）： 169?176.

[5] 周先春，汪美玲，石蘭芳，等.基于梯度與曲率相結合的圖像平滑模型的研究[J].物理學報，2015，64（4）：136?142.

ZHOU X C， WANG M L， SHI L F， et al. Research on image smoothing model based on gradient and curvature [J]. Acta physica sinica， 2015， 64（4）： 136?142.

[6] 吳登輝，周先春，陳銘.基于四階非線性偏微分方程的圖像去噪算法[J].電子測量與儀器學報，2017，31（6）：839?843.

WU D H， ZHOU X C， CHEN M. Image denoising algorithm based on nonlinear fourth?order PDE [J]. Journal of electronic measurement and instrumentation， 2017， 31（6）： 839?843.

[7] 周先春，汪美玲，石蘭芳，等.基于小波與重調和方程的擴散去噪模型的研究[J].物理學報，2015，64（6）：148?156.

ZHOU X C， WANG M L， SHI L F， et al. Study of diffusion denoising model based on Wavelet and biharmonic equation [J]. Acta physica sinica， 2015， 64（6）： 148?156.

[8] 汪美玲，周先春，周林鋒，等.全變分耦合圖像去噪模型[J].通信學報，2016，37（4）：182?191.

WANG M L， ZHOU X C， ZHOU L F， et al. A fully variational coupled image denoising model [J]. Journal on communications， 2016， 37（4）： 182?191.

[9] ZHANG K， ZUO W， CHEN Y， et al. Beyond a gaussian denoiser： residual learning of deep CNN for image denoising [J]. IEEE transactions on image processing， 2017， 26（7）： 3142?3155.

[10] 黃金，周先春，吳婷，等.混合維納濾波與改進型TV的圖像去噪模型[J].電子測量與儀器學報，2017，31（10）：1659?1666.

HUANG Jin， ZHOU Xianchun， WU Ting， et al. Image denoising model based on mixing Wiener filtering and improved total variation [J]. Journal of electronic measurement and instrumentation， 2017， 31（10）： 1659?1666.