五對(duì)角緊致差分格式優(yōu)化及二維聲波傳播波動(dòng)方程數(shù)值模擬

汪 勇,穆鵬飛,蔡文杰,王 鵬,桂志先

(1.油氣資源與勘探技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室(長(zhǎng)江大學(xué)),湖北武漢430100;2.長(zhǎng)江大學(xué)地球物理與石油資源學(xué)院,湖北武漢430100;3.中海石油(中國(guó))有限公司天津分公司,天津300450)

地震波場(chǎng)有限差分?jǐn)?shù)值模擬[1-9]是研究復(fù)雜地區(qū)地震資料采集、處理和解釋的有效輔助手段,也是逆時(shí)偏移和全波形反演的基礎(chǔ)。緊致有限差分格式是其中一種具有較高計(jì)算效率的方法,與常規(guī)中心差分格式相比,它能夠使用更少的計(jì)算節(jié)點(diǎn)達(dá)到相同的計(jì)算精度,減少了計(jì)算量和所需的存儲(chǔ)空間。此外,緊致差分格式是一種隱式差分格式,使用該格式計(jì)算空間導(dǎo)數(shù)時(shí),不僅用到了待求網(wǎng)格點(diǎn)周圍的函數(shù)值,還用到了相鄰節(jié)點(diǎn)的導(dǎo)數(shù)值,具有更低的數(shù)值頻散誤差,因而能夠使用更粗的網(wǎng)格計(jì)算,提高數(shù)值模擬的計(jì)算效率。因此緊致差分格式被廣泛應(yīng)用于聲波、彈性波和復(fù)雜介質(zhì)等的地震波場(chǎng)數(shù)值模擬[10-17]。

在地震波場(chǎng)有限差分?jǐn)?shù)值模擬中,需要高精度的空間離散差分算子。差分算子的精度取決于差分系數(shù)和差分階數(shù),差分階數(shù)越高,差分算子越精確,差分精度就越高,數(shù)值頻散越小,但其計(jì)算量也隨之增大。優(yōu)化差分系數(shù)可使差分算子最大程度地逼近空間偏導(dǎo)算子。KIM等[18]利用頻散關(guān)系保持(dispersion-relation-preserving,DRP)的基本思想優(yōu)化了一階導(dǎo)數(shù)的緊致差分格式;LIU等[19]基于頻散關(guān)系提出了優(yōu)化的時(shí)空域有限差分系數(shù),可在不增加計(jì)算成本的情況下顯著提高模擬精度;ZHANG等[20-21]使用最大范數(shù)的目標(biāo)函數(shù)及模擬退火算法求解目標(biāo)函數(shù),對(duì)一階和二階常規(guī)中心差分的差分系數(shù)進(jìn)行了優(yōu)化;LIU[22-23]使用最小平方法優(yōu)化了二階導(dǎo)數(shù)中心差分和一階導(dǎo)數(shù)交錯(cuò)差分系數(shù);YU等[24]基于DRP思想,優(yōu)化得到了5階精度的組合型緊致差分系數(shù);REN等[25]利用優(yōu)化后的時(shí)空域差分格式進(jìn)行了聲波和彈性波方程的數(shù)值模擬;YANG等[26]利用極小極大算法(minimax approximation)優(yōu)化了交錯(cuò)網(wǎng)格差分系數(shù),在保證中低波數(shù)范圍內(nèi)差分格式分辨率的同時(shí),提高了大波數(shù)情況下的模擬精度。

本文首先將二階導(dǎo)數(shù)的五對(duì)角緊致差分格式擴(kuò)展到2N階差分精度,然后基于頻散關(guān)系保持的思想,根據(jù)最小平方法建立了波數(shù)誤差的目標(biāo)函數(shù),利用拉格朗日乘數(shù)法對(duì)目標(biāo)函數(shù)進(jìn)行求解,得到了優(yōu)化后的4～10階精度差分系數(shù)。與KIM等[18]方法相比,除了優(yōu)化目標(biāo)是二階導(dǎo)數(shù)以外,主要區(qū)別在于使用的方程和網(wǎng)格節(jié)點(diǎn)數(shù)不同,KIM等[18]方法在優(yōu)化2～8階精度差分系數(shù)時(shí)均使用了7個(gè)節(jié)點(diǎn),而本文根據(jù)差分精度的不同,使用不同的節(jié)點(diǎn)數(shù),提高了計(jì)算效率。最后,分析和對(duì)比了優(yōu)化前后差分格式的模擬精度、數(shù)值頻散和聲波方程的穩(wěn)定性條件,并應(yīng)用優(yōu)化后的緊致差分格式和基于輔助微分方程的完全匹配層邊界條件對(duì)二階聲波方程進(jìn)行了數(shù)值模擬,驗(yàn)證了方法的精度。

1 二維聲波方程的高階差分近似

根據(jù)彈性力學(xué)分析,二維情況下二階聲波方程(假設(shè)體力為零)可以表示為:

(1)

式中:u(x,z)為聲波位移場(chǎng);v(x,z)為聲波速度場(chǎng);x,z和t分別為空間和時(shí)間坐標(biāo)。

1.1 時(shí)間2M階近似

利用截?cái)嗟奶├展奖硎緉+1和n-1時(shí)刻的位移場(chǎng)可以得到:

式中:i,j和n分別為空間和時(shí)間網(wǎng)格坐標(biāo);Δt為時(shí)間步長(zhǎng)。兩式相加,略去高次項(xiàng),得到位移場(chǎng)時(shí)間2M階精度的差分格式:

(4)

當(dāng)M=1時(shí),根據(jù)聲波方程((1)式),將(4)式中位移對(duì)時(shí)間的導(dǎo)數(shù)轉(zhuǎn)化為位移對(duì)空間的導(dǎo)數(shù),即可得時(shí)間二階精度的差分格式:

(5)

當(dāng)M=2時(shí),同理可得時(shí)間四階精度的差分格式:

(6)

公式(5)和公式(6)為位移場(chǎng)的三層顯式差分格式,利用它們就可以進(jìn)行地震波場(chǎng)時(shí)間層的推進(jìn)計(jì)算。公式中含有位移u對(duì)x和z的二階和四階導(dǎo)數(shù),這些導(dǎo)數(shù)將利用緊致差分格式進(jìn)行求取。

1.2 空間2N階緊致差分近似

1992年,LELE[27]對(duì)埃爾米特(Hermite)公式進(jìn)行了擴(kuò)展,構(gòu)造了求解函數(shù)f(x)二階導(dǎo)數(shù)的緊致差分格式為:

(7)

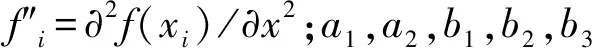
對(duì)公式(7)進(jìn)行擴(kuò)展,可以構(gòu)造二階導(dǎo)數(shù)的2N階精度緊致差分格式。由于公式(7)左邊有5項(xiàng),系數(shù)矩陣為五對(duì)角矩陣,所以稱為五對(duì)角緊致有限差分格式(pentadiagonal compact finite difference,簡(jiǎn)稱CFD5),表示為:

(8)

從公式(8)可以看出,CFD5格式只需要利用2N-3個(gè)節(jié)點(diǎn)即可達(dá)到2N階差分精度。利用泰勒級(jí)數(shù)展開和待定系數(shù)法以及下列方程組((9)式)可以求得CFD5格式2N(N≥3)階差分精度的差分系數(shù),表1列出了6～12階精度CFD5格式差分系數(shù)。

(9)

利用公式(8)所表示的CFD5格式,可以求取公式(5)和公式(6)中的位移對(duì)空間的二階偏導(dǎo)數(shù)?2u/?x2和?2u/?z2,差分格式寫成矩陣形式為:

(10)

其中,

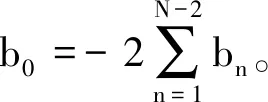
根據(jù)公式(10)即可求得空間二階導(dǎo)數(shù)?2U/?x2和?2U/?z2的2N(N≥3)階空間差分精度近似值,表示為:

(11)

此外,公式(6)中的四階偏導(dǎo)數(shù)和混合偏導(dǎo)數(shù),可以利用公式(11)對(duì)二階偏導(dǎo)數(shù)再次求導(dǎo)進(jìn)行求取。

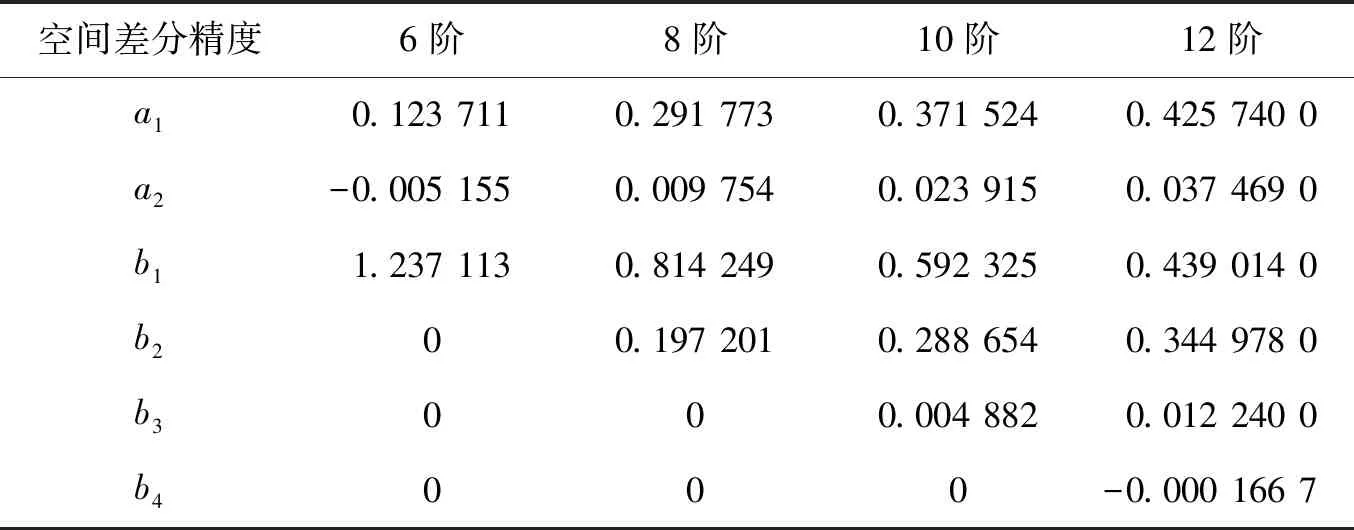
表1 五對(duì)角緊致差分格式二階導(dǎo)數(shù)的差分系數(shù)

2 二階導(dǎo)數(shù)緊致格式的差分系數(shù)優(yōu)化及分析

地震波場(chǎng)數(shù)值模擬中,為了得到清晰的波場(chǎng)記錄,需要高精度的空間離散差分算子。精度越高的差分算子數(shù)值頻散越小,但算子長(zhǎng)度越大,計(jì)算量也越大。優(yōu)化差分系數(shù)可使差分算子最大程度地逼近空間偏導(dǎo)算子,本節(jié)基于頻散關(guān)系保持的基本思想,對(duì)二階導(dǎo)數(shù)的緊致差分系數(shù)進(jìn)行優(yōu)化,提高緊致差分格式的分辨率。

2.1 優(yōu)化差分系數(shù)

首先對(duì)CFD5格式(公式(8))進(jìn)行數(shù)值頻散分析,令:

(12)

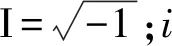
將公式(12)代入公式(8)中可以得到(2N階精度):

(13)

利用歐拉公式,并將B=-(k′)2A代入(13)式可得:

(14)

令ω=kh,ω′=k′h,則ω′可以表示為:

(15)

ω和ω′分別是真波數(shù)和數(shù)值波數(shù)與空間步長(zhǎng)的乘積,在理想情況下,如果不存在數(shù)值頻散,則ω′=ω。它們的差別越大,則說(shuō)明該方法的數(shù)值頻散越嚴(yán)重,反之則說(shuō)明該方法能更好地壓制數(shù)值頻散。

下面以3點(diǎn)6階格式為例來(lái)說(shuō)明差分系數(shù)的優(yōu)化方法。由公式(8)可以得到:

(16)

公式(16)中的差分系數(shù)a1,a2和b1為了滿足2階和4階精度泰勒公式截?cái)嗾`差的要求,必須滿足方程組:

(17)

按照TAM等[28]提出的DRP思路,在某個(gè)選定的波數(shù)范圍內(nèi),確定公式(17)中的3個(gè)未知差分系數(shù)a1,a2和b1,使得數(shù)值波數(shù)k′盡可能地接近真波數(shù)k。為了消除數(shù)值波數(shù)表達(dá)式中的根號(hào),簡(jiǎn)化計(jì)算,定義誤差函數(shù)為:

(18)

其中,W(ω)為一個(gè)加權(quán)函數(shù),目標(biāo)是使誤差函數(shù)解析可積,它是ω2-ω′2的分母部分。θ是積分上限,取值范圍是θ∈(0,π),取值大小與差分精度有關(guān),一般低階取小值,高階取大值。它的取值不同,計(jì)算出來(lái)的差分系數(shù)也不同,這里θ=5π/8。

選定a1為變量,由方程(17)可得b1=(36a1+24)/23,a2=(1-10a1)/46。確定E的最小值為條件極值問(wèn)題,采用拉格朗日乘數(shù)法進(jìn)行求解,即根據(jù)?E/?a1=0,可以得到:

(19)

由公式(17)、公式(18)和(19)可以確定3個(gè)優(yōu)化后的差分系數(shù),a1=0.127658,a2=-0.006013,b1=1.243290。將上述差分系數(shù)代入公式(8),則得到優(yōu)化后的4階精度五對(duì)角緊致差分格式(pentadiagonal optimized compact finite difference,以下簡(jiǎn)稱OCFD5)。采用同樣的方法,對(duì)公式(8)表示的CFD5格式進(jìn)行差分系數(shù)優(yōu)化,優(yōu)化后的4～10階差分系數(shù)見表2。為了方便,將二階導(dǎo)數(shù)的2N階精度優(yōu)化前后的緊致差分格式統(tǒng)一表示為:

(20)

CFD5:L=N-2,N≥3,a1,a2和bl見表1。OCFD5:L=N-1,N≥2,a1,a2和bl見表2。

若要達(dá)到2N階空間差分精度,優(yōu)化前的CFD5方法需要利用2N-3個(gè)節(jié)點(diǎn),優(yōu)化后的OCFD5方法需要使用2N-1個(gè)節(jié)點(diǎn)。

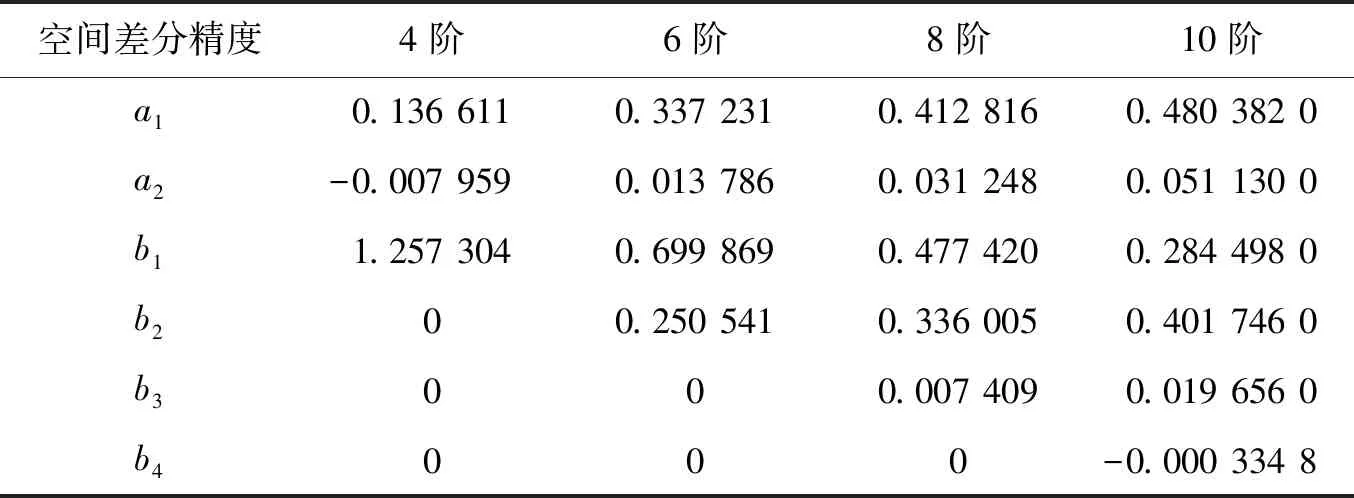
表2 二階導(dǎo)數(shù)的五對(duì)角優(yōu)化緊致差分格式的差分系數(shù)

由于不同的積分上限可以得到不同的差分系數(shù),這里補(bǔ)充說(shuō)明積分上限選取的原則。通過(guò)選取θ=3π/8～7π/8,可以得到不同的差分系數(shù),表3為4階精度差分格式優(yōu)化時(shí),不同積分上限時(shí)得到差分系數(shù)。由不同的差分系數(shù)可以得到各自的波數(shù)比曲線,如圖1所示,其中波數(shù)比定義為數(shù)值波數(shù)與真波數(shù)之比,表示為R=k′/k=k′h/kh=ω′/ω。

由4階精度格式優(yōu)化結(jié)果可以看出(圖1a),當(dāng)θ=5π/8,波數(shù)比曲線接近1的范圍最大。θ取值較小時(shí),有效的波數(shù)范圍較小,達(dá)不到優(yōu)化的目的;θ取值過(guò)大時(shí),曲線向上偏離1,也會(huì)造成數(shù)值頻散。定量來(lái)看,若給定頻散誤差標(biāo)準(zhǔn)E=|R-1|≤0.2%,當(dāng)積分上限θ=3π/8,4π/8,5π/8,6π/8,7π/8時(shí),波數(shù)比R滿足誤差標(biāo)準(zhǔn)的最大ω分別為1.55,1.69,1.92,1.12和0.96。也就是說(shuō),當(dāng)θ=5π/8時(shí)的滿足誤差標(biāo)準(zhǔn)的波數(shù)范圍最寬,能在最大的范圍內(nèi)壓制數(shù)值頻散。圖1b到圖1d是6,8,10階OCFD5格式在不同積分上限時(shí)得到的波數(shù)比曲線,與4階精度時(shí)確定積分上限和對(duì)應(yīng)優(yōu)化系數(shù)的原則類似,確定6階和8階時(shí)的積分上限θ=6π/8,10階時(shí)的積分上限θ=7π/8。由于篇幅所限,6～10階不同積分上限時(shí)的差分系數(shù)不具體列出。

2.2 頻散分析

CFD5格式和OCFD5格式的數(shù)值波數(shù)與真波數(shù)之比R可以表示為:

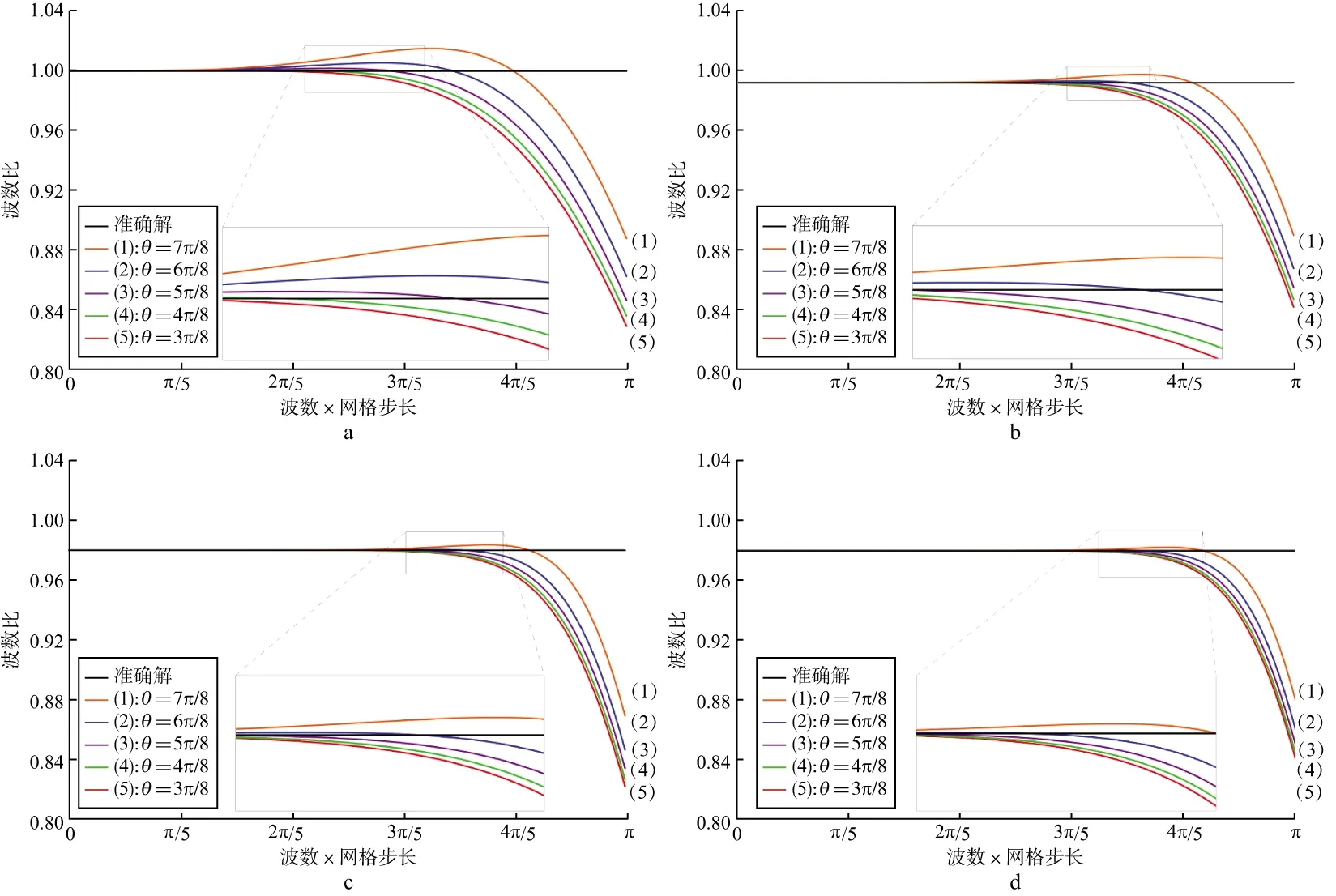
圖1 不同積分上限θ優(yōu)化后格式的波數(shù)比曲線a 4階精度; b 6階精度; c 8階精度; d 10階精度

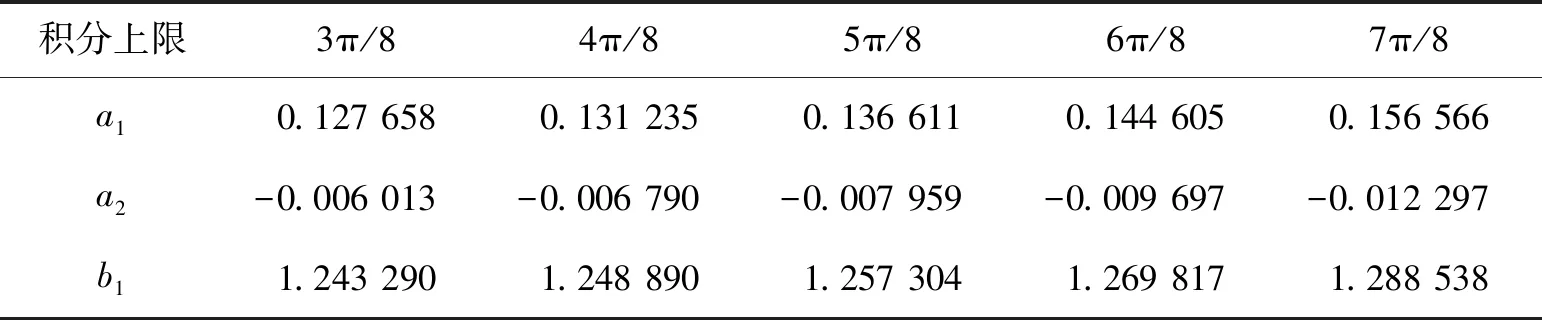
積分上限3π/84π/85π/86π/87π/8a10.1276580.1312350.1366110.1446050.156566a2-0.006013-0.006790-0.007959-0.009697-0.012297b11.2432901.2488901.2573041.2698171.288538

(21)

在理想情況下,即不存在數(shù)值頻散時(shí),R恒等于1。R偏離1越大,說(shuō)明該方法的數(shù)值頻散越嚴(yán)重,反之則說(shuō)明該方法能更好地壓制數(shù)值頻散。使用表1和表2中不同精度的差分系數(shù),可以計(jì)算得到CFD5和OCFD5格式的波數(shù)比曲線,如圖2所示。

由圖2波數(shù)比曲線可以看出:①在相同的差分精度情況下,優(yōu)化后的格式比優(yōu)化前的波數(shù)比曲線更接近1,所以每個(gè)波長(zhǎng)內(nèi)需要的最少采樣點(diǎn)數(shù)更少,這說(shuō)明優(yōu)化過(guò)程起到了提高壓制數(shù)值頻散的作用,數(shù)值計(jì)算時(shí)能使用更大的空間網(wǎng)格,從而減少了計(jì)算內(nèi)存,提高了計(jì)算效率;②優(yōu)化后的2N階精度格式,波數(shù)比曲線比2N+2階精度優(yōu)化前的頻散誤差更小,例如圖2a中的4階OCFD5要好于6階的CFD5。由圖2b到圖2d也可以得出相同結(jié)論。

2.3 差分精度分析

進(jìn)行數(shù)值模擬時(shí),在時(shí)間差分精度相同的條件下,不論是利用優(yōu)化前的CFD5格式,還是利用優(yōu)化后的OCFD5格式,它們?cè)跁r(shí)間層遞推方式上是相同的,不同之處僅在于空間偏導(dǎo)數(shù)近似值求取時(shí)的差分格式不同。為了比較它們的近似精度,需要對(duì)其截?cái)嗾`差進(jìn)行對(duì)比,結(jié)果見表4。從表4中可以看出,在兩種方法達(dá)到同樣空間近似精度的條件下,優(yōu)化后的格式具有更小的截?cái)嗾`差,例如6階精度時(shí)的CFD5截?cái)嗾`差約為OCFD5的3.69倍。

利用一維平面簡(jiǎn)諧波初值問(wèn)題的解析解來(lái)比較優(yōu)化前后格式的數(shù)值模擬精度。一維平面諧波初值問(wèn)題可以表示為:

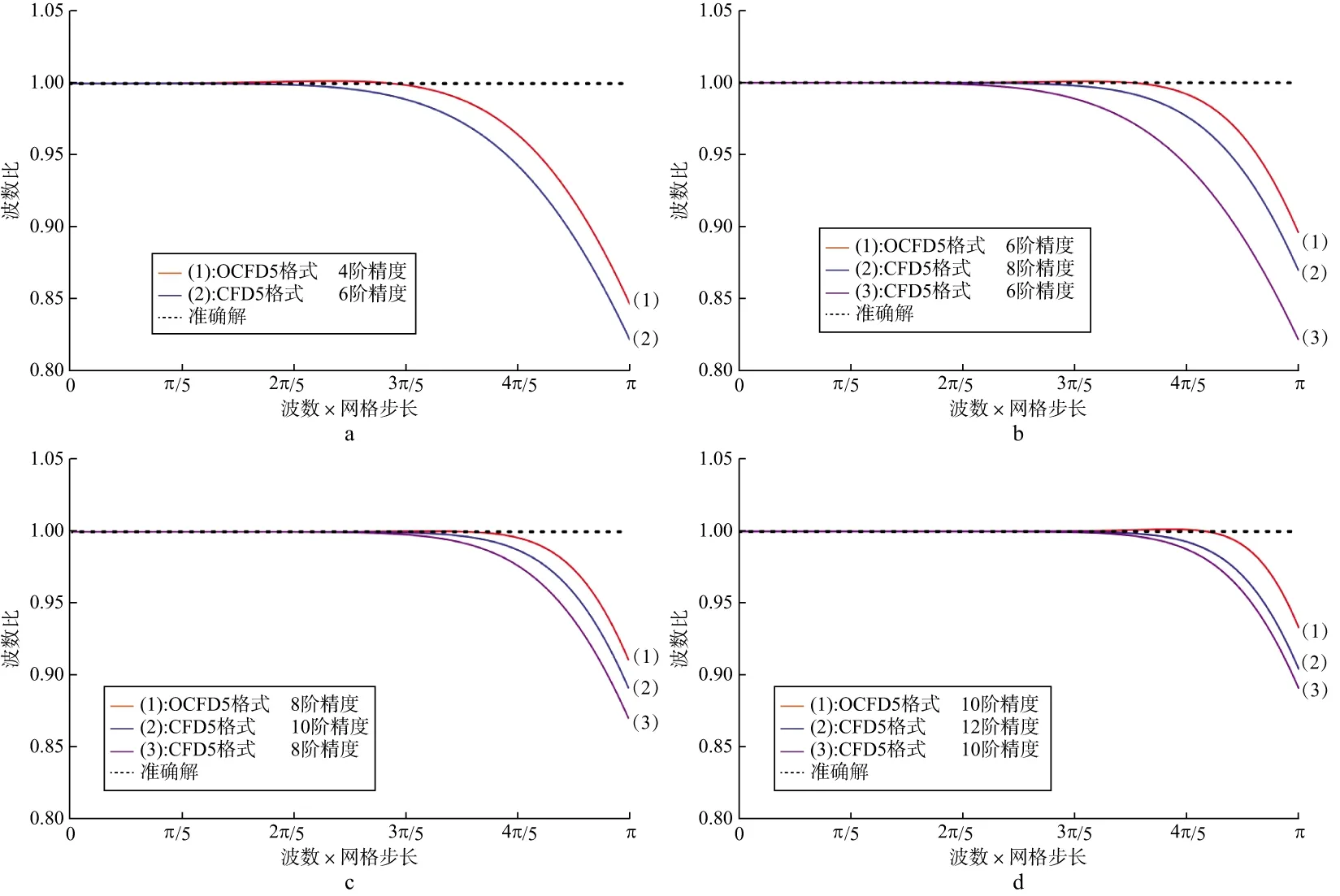
圖2 不同差分精度時(shí)CFD5和OCFD5格式的波數(shù)比曲線a 4階和6階精度比較; b 6階和8階精度比較; c 8階和10階精度比較; d 10階和12階精度比較

表4 優(yōu)化前后格式的二階導(dǎo)數(shù)截?cái)嗾`差主項(xiàng)系數(shù)比較

(22)

式中:v是平面波的波速;f0是平面簡(jiǎn)諧波的頻率。

其初值問(wèn)題的解析解為:

(23)

設(shè)置一維介質(zhì)模型長(zhǎng)度8km,平面波速v=2000m/s,f0=10Hz,數(shù)值模擬時(shí)的時(shí)間步長(zhǎng)2ms,空間網(wǎng)格大小20m。數(shù)值模擬時(shí),兩種差分格式均為時(shí)間4階、空間6階精度。通過(guò)數(shù)值模擬,可得圖3 所示的1s時(shí)刻的位移u的波場(chǎng)快照,圖中藍(lán)色實(shí)線是用公式(23)計(jì)算得到的精確解析解。從圖3可以看出,兩種差分格式模擬精度均很高,圖3a中的3條曲線基本重合,無(wú)明顯誤差。但從局部放大的圖3b 和圖3c來(lái)看,優(yōu)化后的OCFD5格式的數(shù)值模擬結(jié)果與精確的解析解更接近,說(shuō)明優(yōu)化格式的模擬精度得到了提高。

為了避免邊界反射的影響,定量計(jì)算得到1s時(shí)刻3000～5000m區(qū)間的CFD5和OCFD5數(shù)值解與解析解之間的相對(duì)誤差分別為0.1005%和0.0167%。這是由于它們?cè)谟?jì)算空間導(dǎo)數(shù)近似值時(shí)存在不同截?cái)嗾`差大小造成的,這與表4的理論分析結(jié)果一致。相對(duì)誤差定義為:

(24)

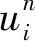
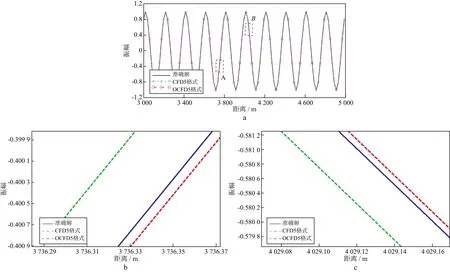
圖3 一維聲波方程數(shù)值模擬快照a 3000～5000m范圍的波場(chǎng)快照; b 圖3a中A部分放大顯示; c 圖3a中B部分放大顯示

2.4 穩(wěn)定性條件

穩(wěn)定性條件是有限差分?jǐn)?shù)值模擬中一個(gè)非常重要的問(wèn)題,是影響差分方法計(jì)算效率的重要因素。我們采用Fourier方法對(duì)公式(5)表示的二維聲波方程的時(shí)間2階、空間2N精度差分格式進(jìn)行穩(wěn)定性分析。

定義:

(25)

式中:kx和kz為x和z方向的視波數(shù);i,j和n分別為空間和時(shí)間網(wǎng)格坐標(biāo);ξ和ζ1為振幅。代入公式(20)中可得:

(26)

令θ1=kxh,-π/2≤θ1≤π/2,并利用歐拉公式,將(26)式化簡(jiǎn)可得:

(27)

解方程可得:

(28)

同理,對(duì)于z方向,定義:

(29)

代入公式(20)同樣可以得到:

(30)

公式(5)是一個(gè)三層顯式差分格式,為了分析其增長(zhǎng)矩陣,將其改寫為:

(31)

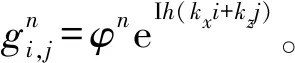
(32)

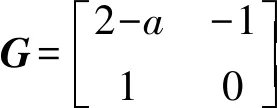
若使差分格式(32)滿足穩(wěn)定性條件,則增長(zhǎng)矩陣G最大特征值的模不大于1,由此可得穩(wěn)定性條件為:

(33)

由公式(28)和公式(30)可以得到:

(34)

所以二維聲波方程的時(shí)間2階、空間2N階精度差分格式的穩(wěn)定性條件可寫為:

(35)

式中:Δt為時(shí)間步長(zhǎng);h為空間網(wǎng)格大小;v為地震波速度;a1,a2和bl為表1和表2中的緊致差分格式差分系數(shù)。

定義α=vΔt/h,穩(wěn)定性條件寫作α≤C(C稱為Courant數(shù)),聲波方程時(shí)間2階精度的CFD5和OCFD5格式的穩(wěn)定性條件如表5所示。從表5來(lái)看,C隨時(shí)間差分精度的增加而增加,隨空間差分精度的增加而減小。在同樣的差分精度條件下,優(yōu)化后格式的穩(wěn)定性條件比優(yōu)化前要略微嚴(yán)格,也就是說(shuō)在相同空間步長(zhǎng)時(shí),允許的時(shí)間步長(zhǎng)要略小。聲波方程時(shí)間4階精度的穩(wěn)定性條件很難給出具體表達(dá)式,表5 給出的不同情況下的穩(wěn)定性條件是根據(jù)試驗(yàn)獲得的。

2.5 邊界條件

在數(shù)值模擬時(shí),由于模型的設(shè)置和計(jì)算模型大小的限制,必然會(huì)存在人工邊界。如果不對(duì)人工邊界進(jìn)行處理,邊界反射會(huì)干擾正常的地震波場(chǎng),所以人工邊界的處理直接影響到數(shù)值模擬的精度和效率。1994年,BERENGER[29]提出的完全匹配層(perfectly matched layer,簡(jiǎn)稱PML)能對(duì)邊界反射起到很好的吸收作用。在此基礎(chǔ)上,DROSSAERT等[30-31]提出的復(fù)頻移完全匹配層(complex frequency shifted perfectly matched layer,簡(jiǎn)稱CFS-PML)能對(duì)近掠入射的低頻波起到更好的衰減作用,而卷積PML[32](convolutional PML)和輔助微分方程PML[33](auxiliary differential equation PML,簡(jiǎn)稱ADE-PML)的優(yōu)點(diǎn)是可以使用非分裂的波動(dòng)方程。針對(duì)二階聲波方程,本文采用輔助微分方程結(jié)合復(fù)頻移完全匹配層[34](ADE-CFS-PML)進(jìn)行邊界處理,略去推導(dǎo)過(guò)程,直接給出x方向控制方程為:

表5 二維聲波方程優(yōu)化前后緊致差分格式的穩(wěn)定性條件

(36)

式中:u1,u2和u3是引入的中間變量,可由(36)式中第一個(gè)方程到第三個(gè)方程依次計(jì)算u3,u2和u1;參數(shù)α′和d′分別是α(x)和d(x)對(duì)x的一階導(dǎo)數(shù)。α(x)和d(x)表示為:

(37)

式中:d(x)是x方向的衰減系數(shù),起到衰減x方向波的作用;αmax=πf0,f0是震源信號(hào)主頻;δ是PML邊界厚度;x是節(jié)點(diǎn)至PML最內(nèi)層邊界的距離。此外,d0=[3vmaxln(1/F)]/(2δ)[35],vmax是地震波傳播的最大速度,F是理論反射系數(shù),表示為lgF=[1-lgN]/lg2-3,N是PML邊界層數(shù),本文N=20。

公式(36)只表示了x方向的控制方程,同樣方法可以得到z方向的控制方程,文中不再贅述。

3 模型試算

3.1 均勻介質(zhì)模型

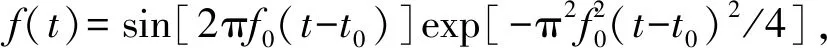
由圖4可以看出:①當(dāng)使用相對(duì)較粗網(wǎng)格計(jì)算時(shí),圖4a所示的6階CFD5格式的波場(chǎng)快照頻散嚴(yán)重,與2.2節(jié)的理論分析結(jié)果一致;②增加網(wǎng)格點(diǎn)數(shù)和差分階數(shù)后,圖4b所示的8階CFD5格式的波場(chǎng)快照的頻散得到了壓制,但頻散還是較為明顯;③圖4c 所示的6階OCFD5格式的波場(chǎng)快照數(shù)值頻散明顯減弱,模擬結(jié)果不僅優(yōu)于優(yōu)化前同階精度的圖4a,也好于差分精度更高的圖4b;④圖4d所示的8階OCFD5格式的波場(chǎng)快照清晰,波形光滑,無(wú)明顯數(shù)值頻散。優(yōu)化前后波場(chǎng)快照的比較結(jié)果,說(shuō)明了本文基于DRP思路進(jìn)行優(yōu)化的結(jié)果達(dá)到了壓制數(shù)值頻散的目的。

圖4 不同差分格式計(jì)算的1000ms時(shí)刻波場(chǎng)快照a CFD5 (4,6); b CFD5 (4,8); c OCFD5(4,6); d OCFD5(4,8)

基于該模型進(jìn)行計(jì)算效率分析,結(jié)果如表6所示。表6中所取空間網(wǎng)格大小滿足波場(chǎng)快照無(wú)數(shù)值頻散要求,同時(shí)為了簡(jiǎn)化分析和避免時(shí)間步長(zhǎng)過(guò)大產(chǎn)生的數(shù)值頻散,時(shí)間步長(zhǎng)均為3ms。4種格式的數(shù)值模擬沒有本質(zhì)的差別,計(jì)算中需要的變量(數(shù)組)個(gè)數(shù)一樣,只是差分系數(shù)和算子長(zhǎng)度不同,它們均在相同的運(yùn)行環(huán)境和程序下進(jìn)行數(shù)值模擬。從表6中可以看出,優(yōu)化后的格式由于能使用更粗的網(wǎng)格計(jì)算,所以單個(gè)變量的網(wǎng)格數(shù)降低,既減少了內(nèi)存的占用,也減少了計(jì)算時(shí)間,從而提高了數(shù)值模擬的計(jì)算效率。

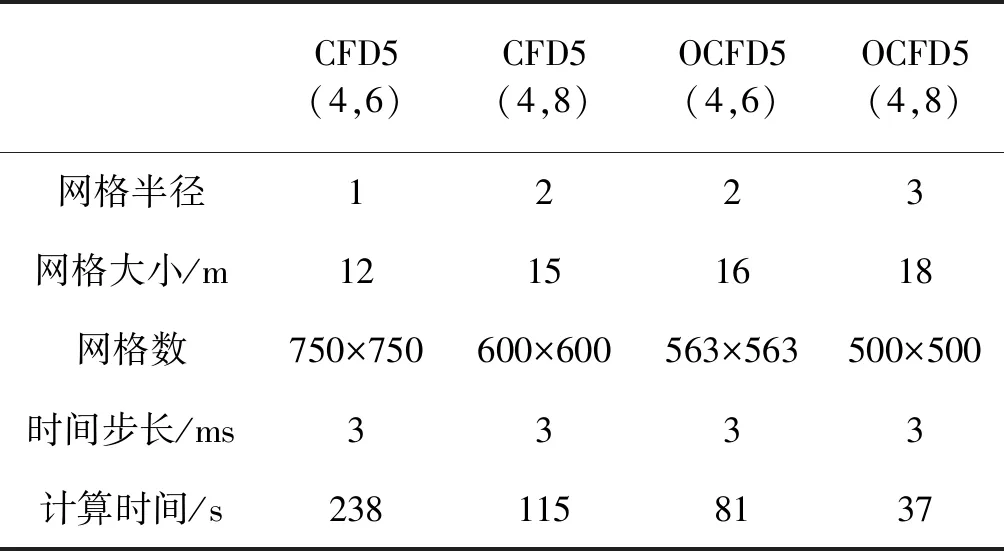
表6 不同方法計(jì)算效率比較

3.2 Marmousi模型

為了驗(yàn)證優(yōu)化后的緊致差分格式對(duì)復(fù)雜介質(zhì)的適用性,用經(jīng)典的二維Marmousi縱波速度模型進(jìn)行數(shù)值模擬。模型如圖5所示,速度v的范圍是1729～5500m/s。模型大小為501×501個(gè)網(wǎng)格點(diǎn),空間網(wǎng)格12m,時(shí)間步長(zhǎng)1ms,震源位于(x=3000m,z=0)位置,激發(fā)震源采用30Hz的Ricker子波,采樣時(shí)間4s,利用ADE-CFS-PML邊界條件對(duì)人工邊界反射進(jìn)行吸收處理。

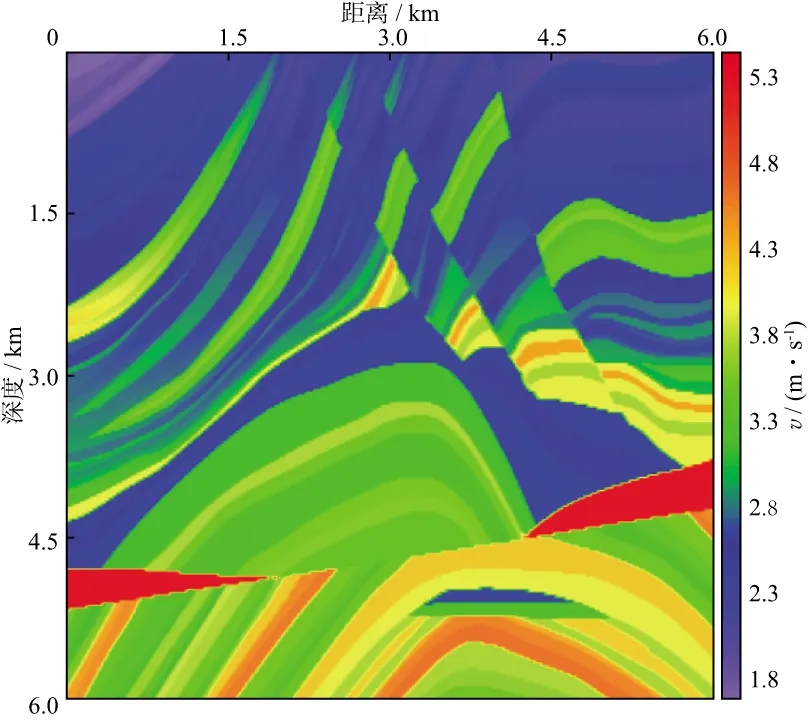
圖5 Marmousi縱波速度模型

圖6給出了采用OCFD5(2,6)格式對(duì)Marmousi模型進(jìn)行聲波方程數(shù)值模擬得到的不同時(shí)刻的波場(chǎng)快照。從圖6可以看出,Marmousi模型中地震波場(chǎng)復(fù)雜且清晰,能夠反映地震波的傳播特征。同時(shí),邊界反射吸收效果較好,無(wú)明顯邊界反射,說(shuō)明本文差分方法在ADE-CFS-PML邊界條件下,對(duì)邊界反射起到了很好的衰減作用。

圖7是分別使用優(yōu)化前后格式得到的地震記錄,精度均為時(shí)間2階、空間6階。為了顯示清晰,對(duì)地震記錄進(jìn)行了瞬時(shí)自動(dòng)增益控制(AGC)處理,時(shí)窗2s。

從圖7中方框所示范圍內(nèi)的地震波場(chǎng)來(lái)看,優(yōu)化前CFD5格式的數(shù)值模擬結(jié)果出現(xiàn)了較嚴(yán)重的數(shù)值頻散,干擾了正常的地震波場(chǎng),不利于波場(chǎng)特征分析及其它處理;而優(yōu)化后OCFD5格式的數(shù)值模擬結(jié)果,模擬精度高,無(wú)明顯數(shù)值頻散。同時(shí),直達(dá)波、反射波及繞射波等波型清晰可見,且邊界吸收效果較好,無(wú)明顯邊界反射,驗(yàn)證了本文算法對(duì)復(fù)雜模型的適用性。

圖6 Marmousi模型OCFD5(2,6)格式聲波模擬波場(chǎng)快照a 400ms; b 800ms; c 1200ms; d 1600ms

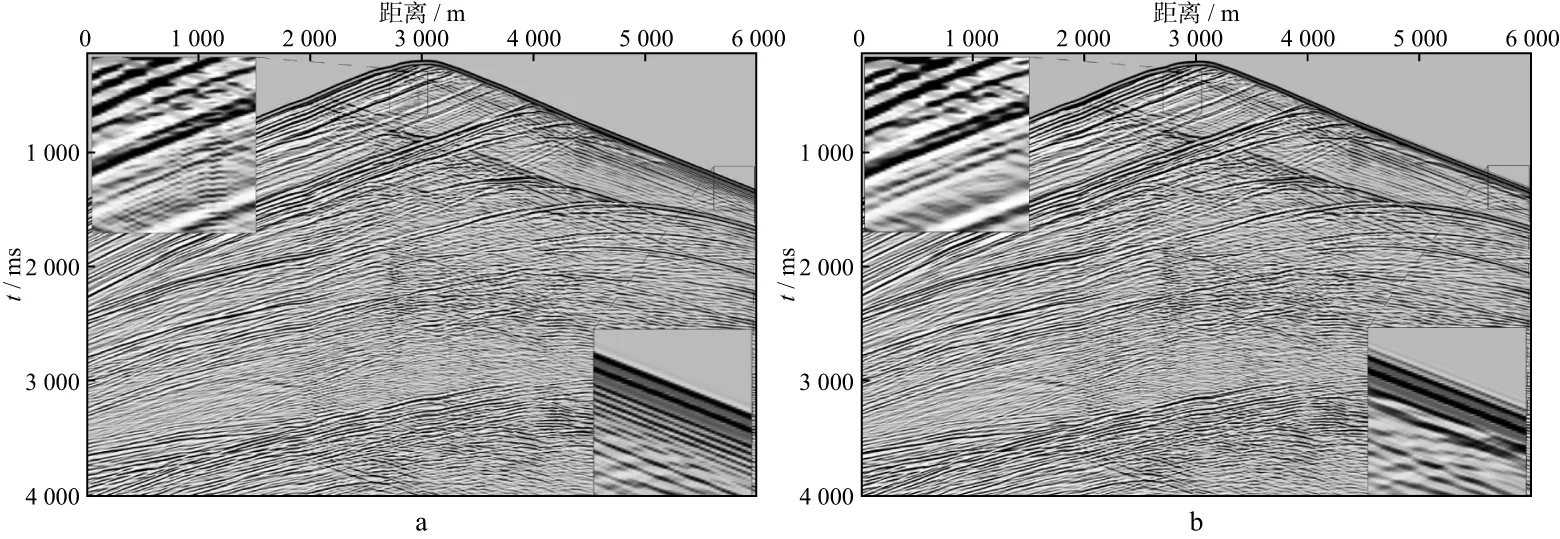
圖7 Marmousi模型CFD5(a)格式和OCFD5(b)格式模擬的地面地震記錄

4 結(jié)論與建議

本文基于頻散關(guān)系保持的思想,利用最小平方法和拉格朗日乘數(shù)法對(duì)二階導(dǎo)數(shù)的五對(duì)角緊致差分格式的差分系數(shù)進(jìn)行了優(yōu)化,研究認(rèn)為:

1) 同為2N階差分精度時(shí),優(yōu)化后的差分格式具有更小的數(shù)值頻散和截?cái)嗾`差,能夠使用更粗的網(wǎng)格進(jìn)行地震波場(chǎng)數(shù)值模擬,節(jié)省了計(jì)算內(nèi)存,更加適用于粗網(wǎng)格下的大尺度的地震波場(chǎng)數(shù)值模擬。

2) 相同網(wǎng)格參數(shù)時(shí),優(yōu)化后2N階OCFD5格式在壓制數(shù)值頻散方面不僅優(yōu)于2N階CFD5格式,也好于2N+2階CFD5格式,也就是可以使用更少的計(jì)算節(jié)點(diǎn)(即算子長(zhǎng)度)的同時(shí)提高計(jì)算效率。

3) 優(yōu)化差分系數(shù)以后,聲波方程的穩(wěn)定性條件要比優(yōu)化前略微嚴(yán)格,但總體上差別不大,Courant數(shù)隨空間差分精度的增加而減小,隨時(shí)間差分精度的增加而增加。

4) 優(yōu)化后差分格式的數(shù)值模擬結(jié)果,地震波場(chǎng)特征清晰,驗(yàn)證了該方法的適用性,為研究地震波傳播規(guī)律、逆時(shí)偏移、全波形反演等工作提供了一種有效的波場(chǎng)延拓方法。

在今后的研究中可以考慮使用不同的優(yōu)化方法,例如樣點(diǎn)逼近、模擬退火法和極小化極大算法等方法,進(jìn)一步提高優(yōu)化差分系數(shù)的效果。