一種類RNN的改進ISTA稀疏脈沖反褶積

潘樹林,閆 柯,楊海飛,蔣從元,秦子雨

(1.西南石油大學地球科學與技術學院,四川成都610500;2.長慶油田長北作業分公司,陜西榆林719000;3.四川職業技術學院電子電氣工程系,四川遂寧629000)

稀疏脈沖反褶積可利用有限帶寬地震記錄反演得到地下反射系數序列,是一種常用的地震資料高分辨率處理方法[1]。該方法在傳統的最小二乘反褶積的基礎上,加一個稀疏先驗約束項,通過求解帶約束的目標函數,進而得到高分辨率的處理結果。求解該目標函數的方法主要有以下兩類。第一類為匹配追蹤類貪婪迭代算法[2-5],直接使用L0范數作為稀疏約束項,通過枚舉匹配迭代的方法求解未知參數。該類方法絕對收斂,但運算量巨大。第二類為CHEN等[6]提出的基追蹤類凸優化算法,此類方法利用L1范數代替L0范數,以便使用線性規劃來求解。該類方法僅在保證期望足夠稀疏時,才能獲得理想的反演結果。為了進一步改善基追蹤類方法對數據稀疏度的要求,張繁昌等[7]、曹靜杰等[8]通過引入地質模型約束和非凸Lp范數正則化方法對其進行了改進。基追蹤類方法結構簡單,便于實現,計算效率高,是當前較主流的求解方法。應用該類方法時,要得到好的反褶積效果,地震子波必須準確,但在實際生產中,難以從地震數據中提取出非常準確的地震子波,因而制約了稀疏脈沖反褶積方法的應用效果。

針對上述問題,國內外學者進行了很多研究。第一類方法為DONOHO等[9]采用過完備字典的方法,通過將地震子波擴充為包含多個頻率成分的過完備字典,消除了單個頻率成分子波帶來的缺點。這類算法最大的特點在于利用多個頻率成分的過完備子波字典代替單個子波字典,求解結果的精度取決于子波字典的準確性。第二類方法為字典學習的方法[10-12],通過學習修改的方式來更新地震子波,但是該類方法只是利用誤差來交替修改反射系數與地震子波,而不是直接通過誤差反傳來修改,因此計算誤差較大。

迭代閾值收縮算法(iterative shrinkage-thresholding algorithm,ISTA)是基追蹤類方法中一種重要的求解算法,其收斂性受輸入子波的影響。循環神經網絡(recurrent neural network,RNN)是一種遞歸神經網絡,可以根據輸入數據進行自主學習,改善處理結果,在很多領域取得了較好的應用效果。本文通過對比ISTA結構和RNN網絡結構,結合兩種方法提出了一種類RNN的改進ISTA稀疏脈沖反褶積方法,該算法是將ISTA轉換為類RNN網絡結構,并引入RNN中BPTT的誤差反傳的思想修改地震子波,克服了子波不準確造成的反演不收斂問題。最后用理論模型數據和吐哈盆地雁木西地區的實際資料對本文方法進行了應用測試。

1 類RNN的改進ISTA原理

1.1 ISTA

稀疏脈沖反褶積可以表達為:

(1)

其中,y表示地震記錄向量,W表示由地震子波組成的矩陣,x表示待求解反射系數向量,λ為正則化參數。

BECK等[13]提出了ISTA,用于求解具有L2-L1結構的復合函數。利用迭代軟閾值的方法求解(1)式,可得:

(2)

(3)

ISTA迭代流程如圖1所示。

圖1 ISTA迭代流程示意

顯然,ISTA求解反射系數的關鍵在于地震子波矩陣We的準確確定,但是在實際應用中,很難準確確定地震子波,所以傳統的ISTA在反褶積應用過程中因為地震子波的問題而存在較大的局限性。

1.2 類RNN的改進ISTA原理

RNN是一種節點定向連接成環的人工神經網絡,其本質特征是在處理單元之間既有內部的反饋連接又有前饋連接,可以在網絡運行中對內部參數不斷進行優化,這是一類適用于處理序列數據的神經網絡,它與基礎的神經網絡最大的不同就是在層之間的神經元也建立了權值連接[14-20]。

圖2為RNN基本結構及展開形式。左側為RNN基本結構,垂向黑色粗箭頭表示“循環”,這意味著RNN的循環體現在隱藏層;右側為RNN展開結構,隱藏層各神經元之間通過不同權值(見小箭頭上的權值符號)連接,即上一步處理的隱藏層(Nt-1)將會影響到下一步處理的隱藏層(Nt)。RNN結構包含了RNN正向計算(黑色細箭頭方向)和反向誤差修正(紅色細箭頭方向)兩個核心內容,其中M和U為計算權值,V為激活函數。本節提出的類RNN的改進ISTA同樣包含了正向計算和反向誤差修正兩個重要環節。

對比圖1和圖2可以發現,ISTA與RNN在結構上有著相似之處。將ISTA中的每一次迭代看作一個時間層,輸入向量中的每一個值看作是一個神經元,軟閾值函數hθ等價于激活函數V,那么ISTA便可以看作一個類似的RNN網絡,如圖3所示。

圖2 RNN基本結構及展開形式

圖3 類RNN的改進ISTA

由圖3可知,矩陣S為循環層參數,即為時間方向參數,We為各層神經元之間的參數,即為層方向參數。

2 改進算法正反向計算方法

2.1 正向算法

由圖2可知,RNN的正向計算可表示為:

(4)

式中:Et為中間變量。

公式(3)可以改寫為如下形式:

(5)

其中,公式(5)中的y相當于公式(4)中的輸入xt,S相當于隱藏層權值M,xk相當于公式(4)中的隱藏層參數Nt,hθ相當于激活函數。

由此可以給出改進ISTA的正向計算流程(圖4),其計算步驟與常規的ISTA一致。

2.2 反向誤差修正算法

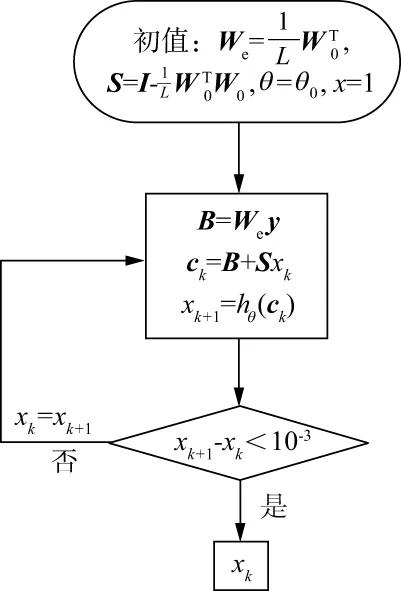
圖4 正向算法流程

圖5中,xr為訓練時給定的反射系數,xk為訓練過程中計算獲得的反射系數,h′為軟閾值求導,Hk,Hk+1為梯度下降過程中的控制函數。由圖5可知,需要先通過迭代逐步反向求解各層誤差,然后求和,得到關于初始輸入的誤差δB、δθ、δWe,進一步利用圖5流程最后一步的梯度下降方法更新這3個參數。

圖5 改進算法的反向誤差修正流程

結合正向算法與反向算法,便可以根據訓練數據多次迭代修改與地震子波有關的參數,得到更好的收斂效果,更加有利于后續的反褶積計算。

3 理論模型數據試算

首先合成了一個不含噪聲的地震單道數據,使用50Hz零相位Ricker子波與第1和第2個反射系數進行褶積,40Hz零相位Ricker子波與第3和第4個反射系數進行褶積,30Hz零相位Ricker子波與第5和第6個反射系數進行褶積,最終得到如圖6所示的理論地震道,該數據包含512個采樣點,6個反射位置。

圖6 理論模型a 地震子波; b 反射系數; c 合成地震記錄

利用圖6中的模型數據,令初始輸入的子波矩陣為零相位40Hz的Ricker子波,結合前文所述的正向算法與反向算法,對初始子波進行修正,經過本文算法優化后的子波如圖7所示,從圖7可以看出,雖然輸入僅有40Hz的子波,但是經過算法自我修正后,可以得到與圖6a多個子波接近的結果,且經過算法修正后獲得的子波集合與期望子波集合基本吻合。使用優化后的子波矩陣進行反褶積處理,得到如圖8所示的結果。給定同樣的初始子波(40Hz的Ricker子波),進行傳統ISTA反褶積方法處理,結果如圖8中藍線所示。

由圖8可見,由于傳統ISTA不具備子波修正能力,當采用40Hz子波作為輸入子波時,算法收斂后計算結果與期望輸出存在明顯差異,反演結果出現了許多虛假信息。而類RNN的改進ISTA在計算過程中不斷優化子波集,最終在不同的位置獲得不同的最優子波。在此基礎上計算的結果明顯優于傳統ISTA。這說明類RNN的改進ISTA能夠通過反向修正子波集合,消除初始輸入子波不準確對反褶積帶來的影響。

為了說明本文方法的抗噪性,在圖6c合成地震記錄的基礎上加入隨機噪聲,得到一個如圖9所示的低信噪比地震記錄,傳統ISTA與本文方法的反褶積結果如圖10所示。

圖7 原始子波與優化后的子波

圖8 傳統ISTA和改進ISTA反褶積處理的結果

圖9 含噪聲地震記錄(信噪比=-4.55dB)

圖10 含噪聲地震記錄反褶積結果

由圖10可以看出,傳統的ISTA在地震資料信噪比較低時,難以獲得準確的反褶積結果,而采用改進ISTA可獲得較為可靠的反褶積結果,說明該方法具有良好的抗噪能力。

4 實際地震資料應用

圖11為吐哈盆地雁木西地區T3井區Line 299線主要目的層段局部地震剖面。分別采用傳統ISTA和改進ISTA對其進行反褶積處理,結果如圖12所示。

對比圖11和圖12可以看出,采用傳統ISTA進行反褶積處理后的剖面整體同相軸變多,變細,且以井旁地震道分辨率提高最為明顯,但是距離井位置越遠處理效果越不明顯(圖12a)。相比之下,采用改進ISTA的反褶積剖面中,不論是井旁道還是距離井位置較遠的地震道,分辨率均得到了顯著提升,且與測井合成記錄的吻合程度大大提高,說明采用改進ISTA的反褶積處理結果可靠。從圖11和圖12中井旁紅色方框中局部放大的地震剖面(圖13)可以看出,采用傳統ISTA處理后,原剖面中部分無法分辨的同相軸得到了有效分離,但是分辨率仍然偏低,而采用改進ISTA處理后的剖面,不僅使原來無法分離的同相軸得到了有效分離,而且同相軸連續性增強,與井資料對比良好,分辨率明顯提高。

圖11 雁木西地區T3井Line 299線主要目的層段局部地震剖面

圖12 采用傳統ISTA(a)和改進ISTA(b)進行反褶積處理的結果(Line299)

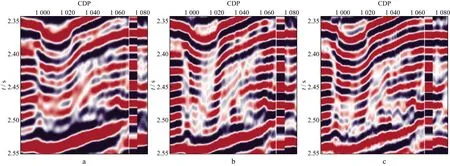
圖13 采用不同方法反褶積結果剖面細節對比(Line299)a 原始剖面;b 傳統ISTA;c 改進ISTA

分別對圖13中的3個剖面進行頻譜分析,結果如圖14所示。顯然,基于改進ISTA的反褶積處理結果有效頻帶寬度從原始剖面的10～40Hz拓展為5～50Hz左右,明顯優于傳統ISTA。

圖14 頻譜對比

5 結論

1) 與傳統的基于ISTA的稀疏脈沖反褶積方法相比,采用類RNN的改進ISTA實施反褶積處理,可以獲得更加穩定、可靠的反褶積處理結果,且方法的抗噪性更佳。

2) 基于類RNN的改進ISTA的稀疏脈沖反褶積方法可極大提高地震資料分辨率。實際資料的處理結果表明,采用該方法可使原始地震資料的有效頻帶拓展約1.5倍,而且除拓展高頻外,還可以極大地保護低頻有效信息,處理結果更有利于進一步儲層精細描述或反演處理。