橋墩高度對群樁-承臺系統動剛度的影響分析

劉建磊，賀相林，張 勇，馬 蒙，王 凱

(1.中國鐵道科學研究院集團有限公司 鐵道建筑研究所，北京 100081；2.朔黃鐵路發展有限責任公司，河北 肅寧 062350)

橋墩基礎靜剛度反映了在外荷載作用下其抵抗變形的能力。當橋墩基礎承載力受沉降變形控制時，豎向靜剛度即反映了橋墩基礎與變形相關的承載能力。測試橋墩基礎的豎向靜剛度有2種方法，其一是直接通過靜載試驗從荷載-沉降曲線的初始線性段獲得，另一種是利用機械阻抗法通過測試動載作用下的橋墩基礎動剛度來間接推算[1-3]。當測試對象為服役橋梁時，后者是唯一可采用的手段。既有研究大多數只分析了單樁動剛度[4-5]，對于常用的群樁-承臺基礎形式，往往不具備直接在樁頂施加動載的條件，取而代之的是在承臺頂部[6]或橋墩頂部施加動載，獲得整個群樁-承臺-橋墩體系的動剛度。

為了獲得群樁-承臺-橋墩體系相對穩定的動剛度值，激振點和拾振點均應合理選取。此外，當需要評估一系列橋墩基礎的豎向動剛度時，不同橋墩墩高的差異對豎向動剛度的影響也不容忽視。為分析上述問題，本文建立了三維動力有限元模型，施加瞬態激勵以分析系統的豎向動剛度值。考慮了激振點分別位于墩頂和承臺頂2種情況，分別分析了這2種激勵情況下，系統豎向動剛度受墩高變化的影響。

1 橋墩-基礎-土層耦合分析模型

利用有限元軟件MIDAS/GTS建立了橋墩-基礎-土層耦合三維動力分析模型(圖1)。土層四周和底部模擬為黏彈性人工邊界。橋墩基礎形式考慮為4根樁組成的群樁-承臺基礎，樁徑1.2 m，承臺尺寸為5.4 m×5.4 m，橋墩截面尺寸為2.4 m×1.8 m，墩身截面不改變，墩高在0～30 m之間變化(墩高為0時即模型中不包括橋墩單元)。在第2，3節中分別在承臺表面和橋墩頂部施加瞬態動力荷載，荷載時程和頻譜曲線見圖2。將距離墩頂中心1，3，5個單元距離的節點定義為墩頂拾振點A1，A3和A5，將承臺頂部距離墩底邊緣1，3，5個單元距離的節點定義為承臺頂部拾振點B1，B3和B5，墩底中心與承臺連接處的節點定義為拾振點C(見圖3)。

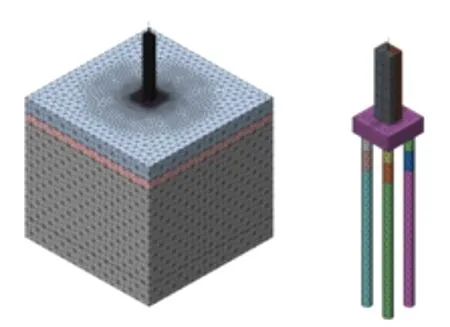
圖1 有限元模型整體及局部示意

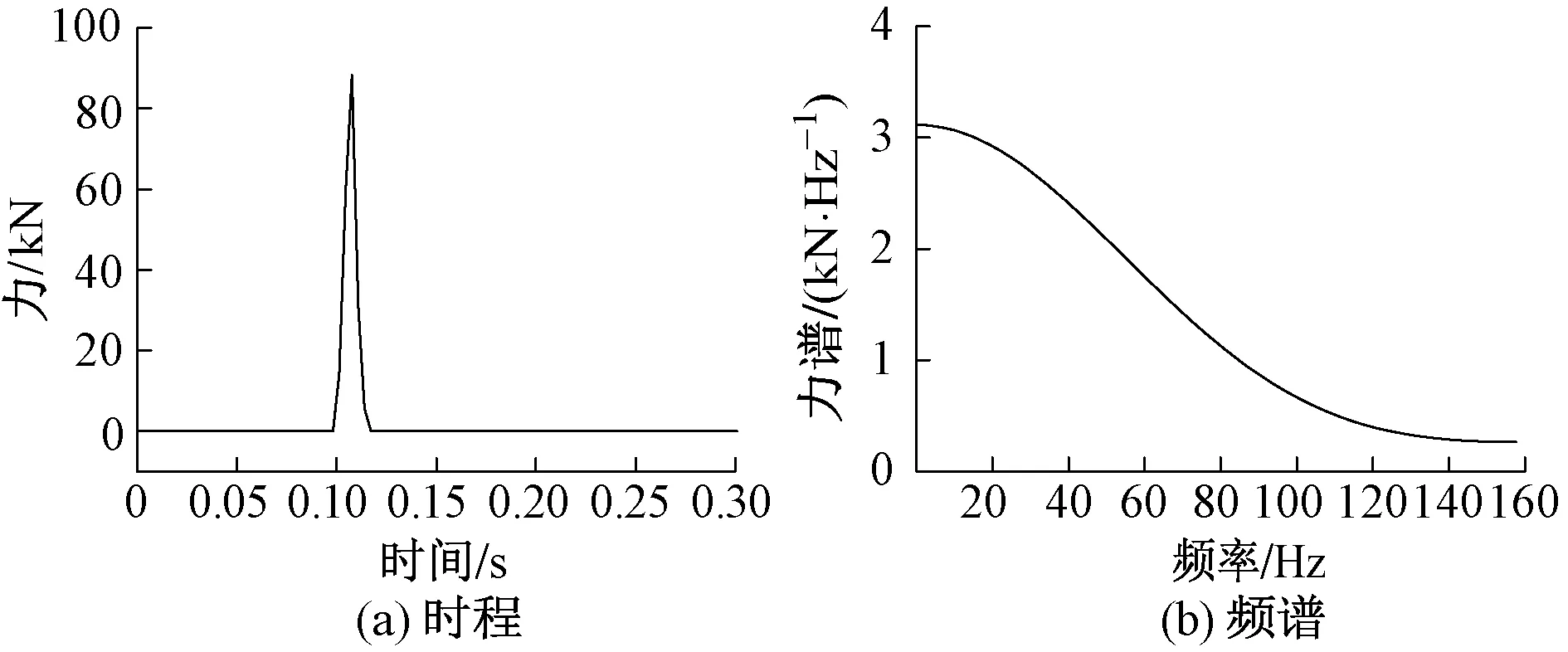
圖2 瞬態激振荷載時程和頻譜曲線

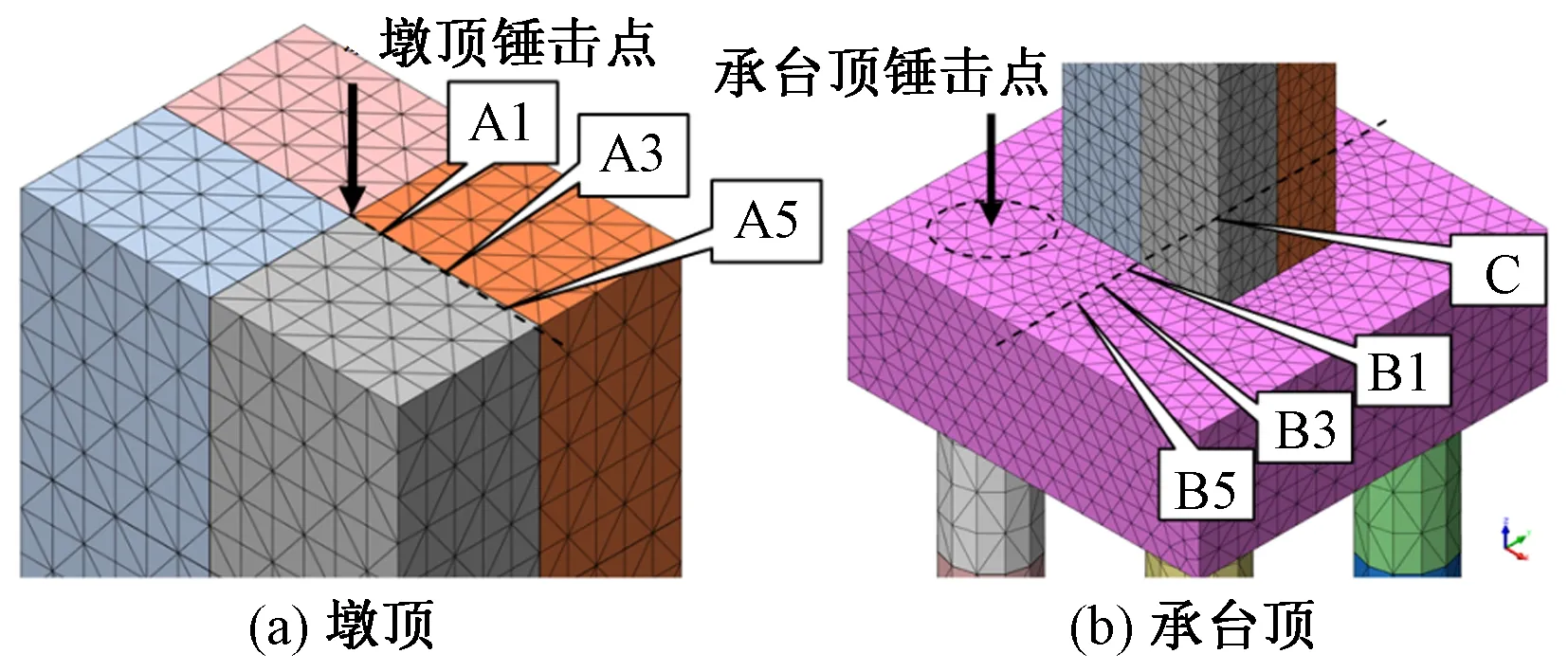
圖3 墩頂和承臺頂部拾振點示意

機械阻抗法測試中，動剛度函數Kd(f)定義為

(1)

式中:F(f)為激振頻譜;v(f)為拾振點速度響應頻譜;f為頻率;v(f)/F(f)表示速度導納。

當作用在結構上的動荷載頻率f→0時，動剛度值趨于靜剛度Ks，即Kd→Ks。激振由于動荷載頻率永遠大于0，因此動剛度也總是大于靜剛度。通常，低頻段(<30 Hz)動剛度值相對穩定，對應低頻段速度導納曲線為一斜率恒定的直線[7]。

實際工程測試時，由于激振質量有限等因素，較難得到穩定性較好的10 Hz以下頻段動剛度值。研究表明[6]：10～30 Hz動剛度值相對穩定。因此，本文在分析動剛度時，選取2.5 Hz和20 Hz兩個代表性頻率，前者反映了理想狀態下一個較低的頻率，后者反映了工程測試中常分析的頻率。

2 錘擊承臺時豎向動剛度分析

2.1 墩高變化對動剛度的影響

當錘擊單根樁所對應承臺頂部時，承臺上拾振點B1動剛度隨墩高變化曲線見圖4(a)。不同頻率下動剛度隨墩高變化趨勢不同。頻率較低時(2.5 Hz)，動剛度值相對穩定，但頻率較高時(如20 Hz)動剛度變化幅度很大：在墩高從6 m變到9 m時，以及從18 m 變到21 m時，動剛度出現兩個增加的突變；其余情況是隨墩高增加動剛度減小。

進一步分析承臺正中C點的動剛度，其變化規律與B1點不同，見圖4(b)。2.5 Hz頻率下動剛度值相對穩定，但20 Hz頻率下動剛度除0 m到3 m出現一個突變值外，動剛度均隨墩高增加緩慢減小。顯然，3 m 墩高的動剛度突變與從無墩到有墩應力場突變有關。

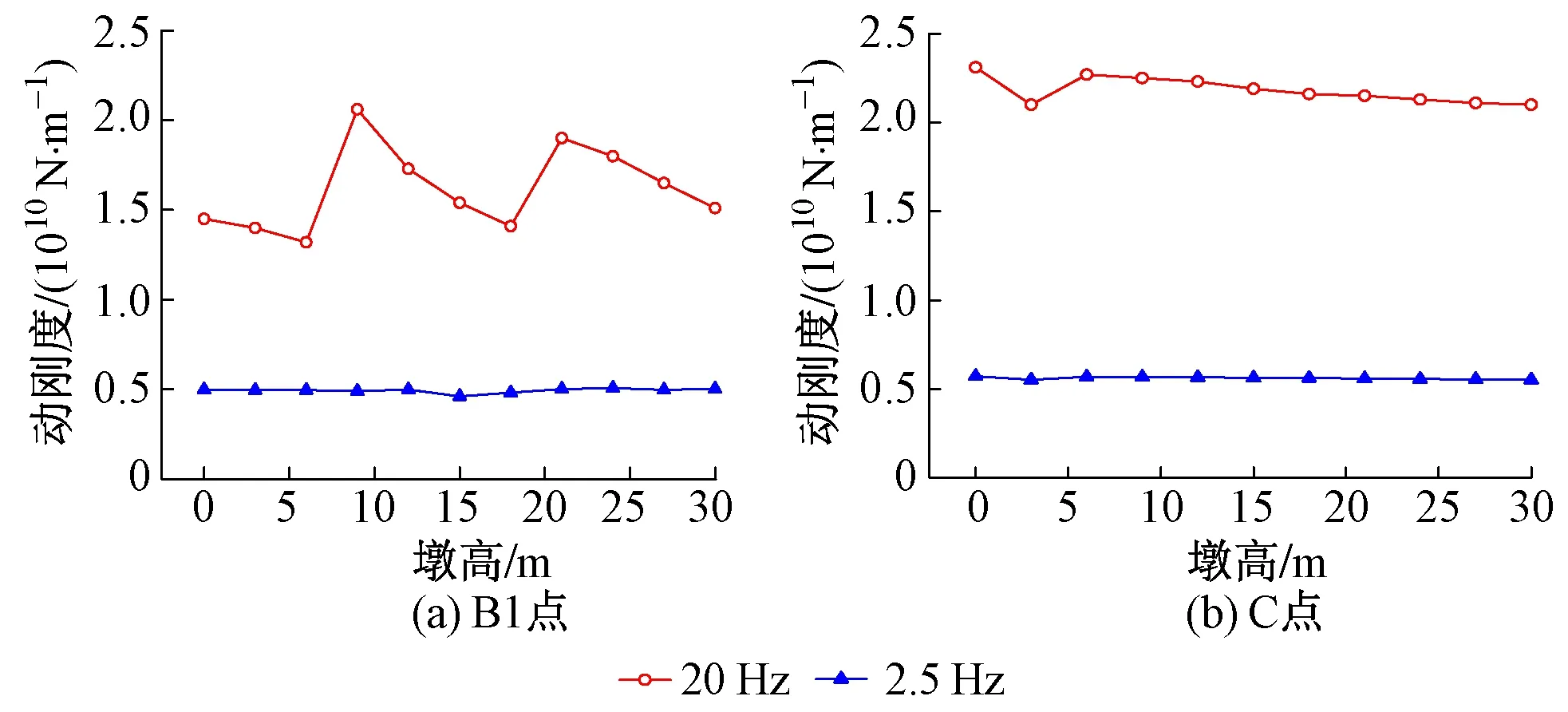
圖4 錘擊承臺頂時B1點和C點動剛度隨墩高變化曲線

2.2 墩高變化對系統模態的影響

在2.1節中，20 Hz時B1點和C點動剛度隨墩高變化表現出完全不同的規律，盡管2個點都位于承臺頂面，但其區別在于C點位于體系對稱中心，而B1點則不是。由于施加沖擊力位于樁頂對應承臺上，是一個非對稱荷載，因此隨著墩高增加，承臺模態不對稱性出現跳躍性漸變可能會引起上述現象。為了證明這一點，進一步分析墩高在0～30 m范圍內變化時，承臺和橋墩系統在100 Hz以內的模態情況，見表1。從表1可見，拾振點B1在20 Hz時動剛度發生突變的點(墩高9,21 m 時)都對應有20 Hz頻率附近模態階數的突變：墩高在0～6 m變化時，20 Hz位于第1階模態之內；墩高為9 m時，20 Hz位于第1，2階模態之間(動剛度突變)；墩高在12～18 m變化時，20 Hz位于第2，3階模態之間；墩高為21 m時，20 Hz位于第3，4階模態之間(動剛度突變)；墩高在24～30 m變化時，20 Hz位于第4，5階模態之間。由此可見，當錘擊位置不在系統對稱點上時，橋墩高度改變對10～30 Hz頻率下動剛度影響較大。

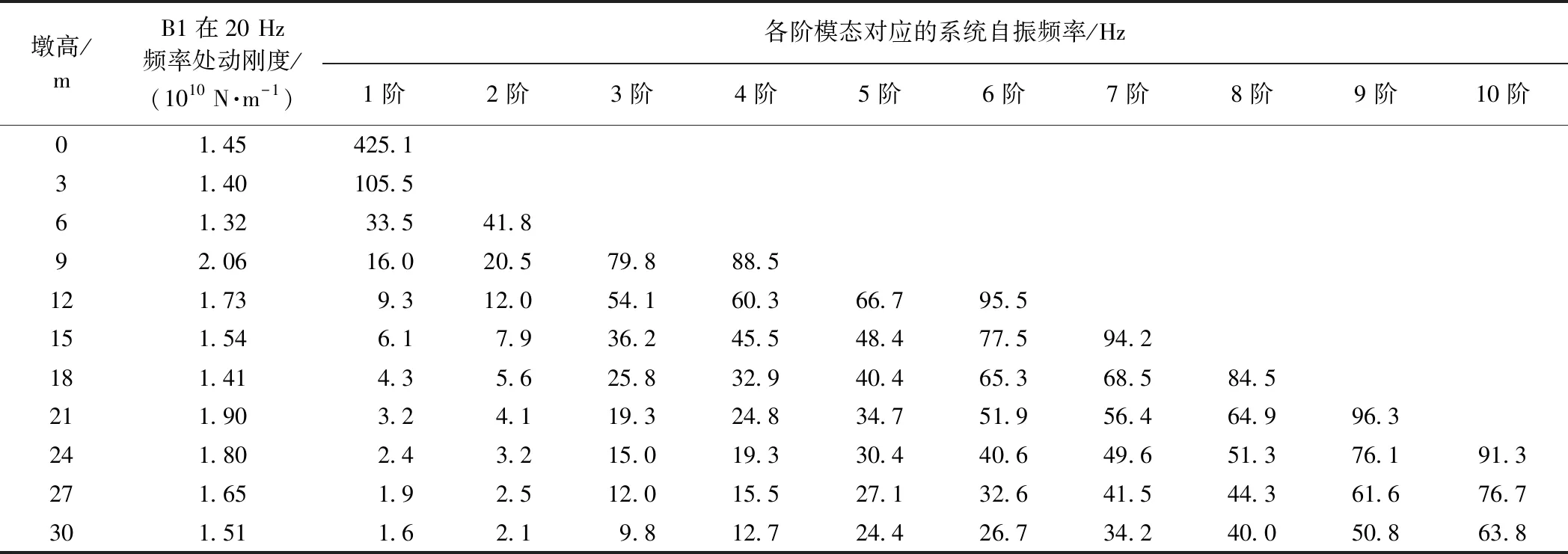
表1 承臺-橋墩系統各階模態自振頻率隨墩高變化情況

3 錘擊墩頂時豎向動剛度分析

當錘擊墩頂中心時，墩頂測點A1，A3和A5在2.5 Hz和20 Hz頻率下的動剛度隨墩高變化曲線見圖5。當錘擊墩頂中心時，承臺頂部測點B1，B3和B5在2.5 Hz和20 Hz頻率下的動剛度隨墩高變化曲線見圖6。可以看出，變化趨勢與第2節中錘擊承臺頂部情況不同：當分析頻率極低時，動剛度數值相對穩定，受墩高影響不大；而當分析頻率為20 Hz時，動剛度均隨墩高增加而單調遞減。

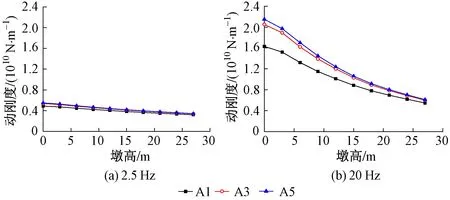
圖5 錘擊墩頂時，墩頂測點A1,A3,A5動剛度隨墩高變化曲線

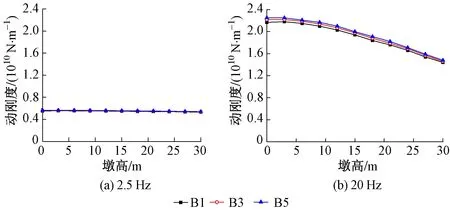
圖6 錘擊墩頂時，承臺頂測點B1,B3和B5動剛度隨墩高變化曲線

為進一步對比不同位置處動剛度隨墩高變化的衰減梯度，將圖5(b)、圖6(b)圖形繪制在同一張圖中分析(圖7)。可以發現：墩高小于15 m時，墩頂和承臺頂在20 Hz時動剛度的衰減梯度有所差異，且墩高越低，衰減梯度差異越明顯。而當墩高大于15 m時，二者衰減梯度趨于一致。

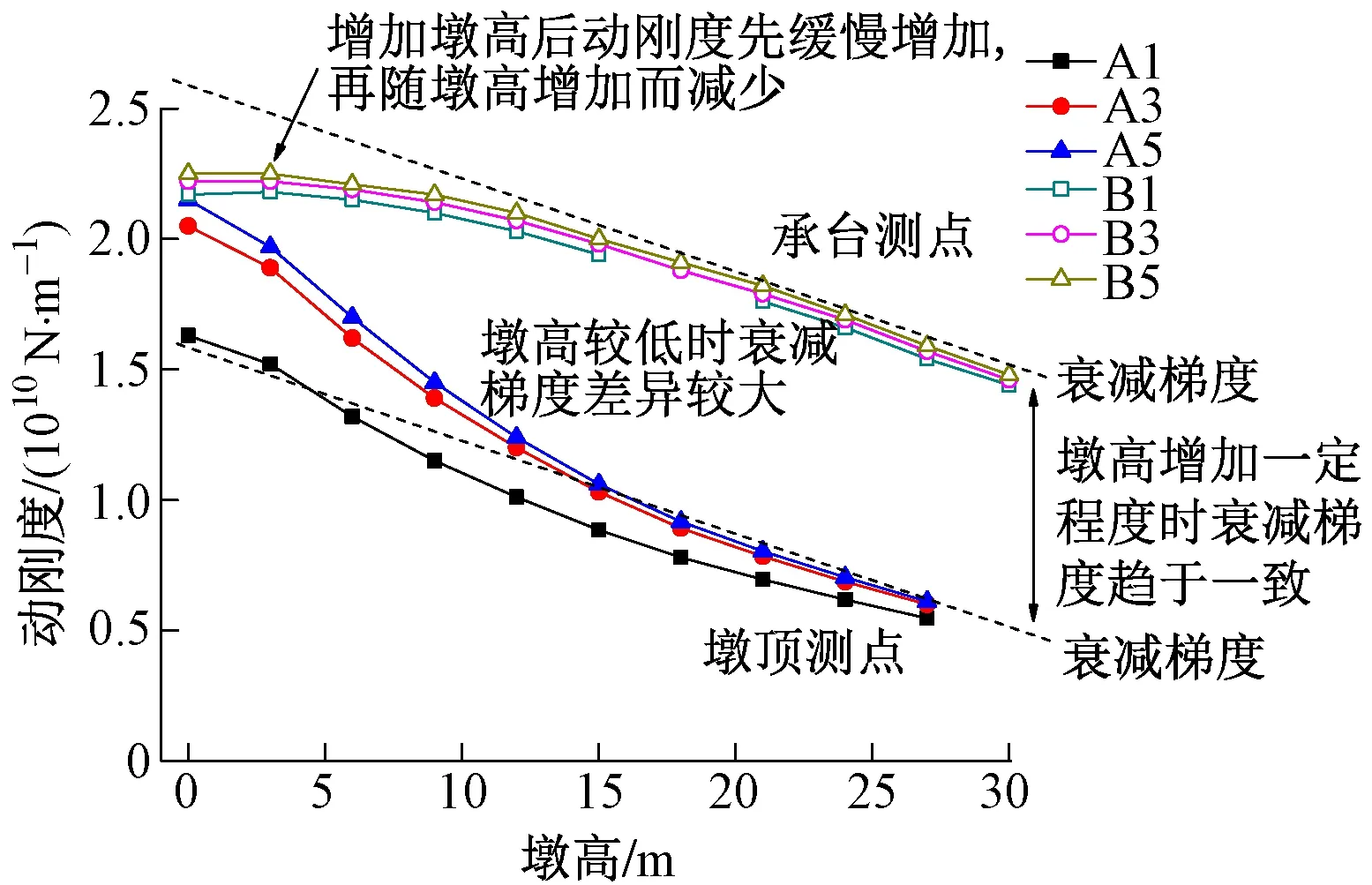
圖7 錘擊墩頂時，墩頂和承臺頂面在20 Hz的動剛度隨墩高變化趨勢

由此可見，如果通過錘擊墩頂獲得系統在20 Hz左右的動剛度，墩高的影響不容忽視。當分析一系列橋墩基礎動剛度時，如果橋墩墩高差異明顯，采用20 Hz 頻率下的動剛度較難作為一個合理指標去估算系統的靜剛度值。

4 結論與建議

通過建立三維動力有限元模型，分析了橋墩高度對群樁-承臺系統動剛度的影響。考慮了激振點位于承臺上和橋墩頂部2種情況，計算結果表明：

1)2種激振點位情況下，2.5 Hz頻率下系統動剛度受橋墩高度變化影響小，計算結果穩定。

2)當激振點位于承臺上時，由于激振點和拾振點均不在結構對稱中心上，因此當頻率較高時(20 Hz左右)，系統動剛度會受到自身模態的影響而發生階躍式突變。

3)當激振點位于墩頂中心時，隨著橋墩高度的增加，20 Hz頻率下的系統動剛度降低。

根據計算結果，當工程中需要測試評估一系列群樁基礎-承臺-橋墩系統的動剛度時，應盡可能取較低的分析頻率。當振源無法激勵出穩定的低頻振動時，建議優先選擇墩頂作為激振點，且應考慮墩身高度對結果進行修正。