基于IGGⅢ的地理加權回歸模型研究

于志英，張福浩，仇阿根，趙陽陽

(中國測繪科學研究院，北京 100830)

地理加權回歸(geographically weighted regression,GWR)是地學領域常用的空間分析方法，被廣泛用于空間非平穩性探測。其基本思想是將采樣點的空間位置嵌入回歸參數中，利用局部加權最小二乘方法逐點進行參數估計。通過構建回歸模型，探究空間模式背后的影響因素或預測空間現象的發展情況。

諸多學者對地理加權回歸模型進行了深入研究。文獻[1]提出了混合地理加權回歸模型，將回歸模型中隨空間位置變化的參數稱為局域參數，不受空間位置影響的參數稱為全域參數，并采用迭代的方法對參數進行近似估計。文獻[2]在此基礎上，對混合地理加權回歸模型進行推導，得到了全域參數和局域參數的精確表達。文獻[3]將時間要素融入地理加權回歸模型，提出了時空地理加權回歸。文獻[4]對時空地理加權回歸模型估計方法、核函數選擇、因子選擇、多重共線性檢驗和參數估計過程進行了詳細介紹。文獻[5]提出了基于半監督的地理加權回歸方法，利用有標記樣本訓練無標記樣本，選擇置信度高的結果擴充有標記樣本，解決了地理加權回歸樣本量較少情況下模型精度不高的問題。文獻[6]針對現有模型無法充分擬合復雜非線性關系的問題，提出了地理時空神經網絡加權回歸模型，有效擬合時間鄰近和空間鄰近的非線性融合作用。另有學者從中間過程出發，對地理加權回歸模型進行改進。文獻[7]將非線性主成分用于回歸模型變量選擇，既避免了變量間的共線性，又保留了原始影響因素的主要信息。文獻[8]用絕對值交叉驗證(absolute value cross-validation，ACV)替代交叉驗證(cross-validation,CV)[9]進行了最優帶寬選取，避免了CV法中二次誤差標準放大離群值的影響。

通過以上研究現狀發現，各方法從不同角度對地理加權回歸模型進行改進，但缺乏異常值檢測與處理過程。因此，本文提出基于IGGⅢ的地理加權回歸模型，將IGGⅢ權函數用于地理加權回歸參數估計過程，對鄰域觀測值進行降權或剔除。首先對方法原理進行詳細介紹，并介紹方法流程，最后將模擬數據和真實數據與GWR、ACV-GWR進行對比試驗，利用均方誤差(mean square error，MSE)、平均絕對誤差(mean absolute error，MAE)和R2作為指標進行評價。

1 基于IGGⅢ的地理加權回歸原理

1.1 方法原理

地理加權回歸模型為

(1)

式中，y為因變量；x為自變量；(u,v)為采樣點位置；βk(ui,vi)為第i個采樣點的第k個參數，β的取值與采樣點位置有關；ε為隨機誤差，符合正態分布。

未知參數β的估計采用最小二乘方法實現。當數據中存在離群值時，離群值參與回歸點的參數估計過程，其二次誤差會主導殘差平方和的值，影響參數估計結果。為削弱鄰域點中的離群值對回歸點參數估計的影響，本文在地理加權回歸模型中引入基于權函數的粗差處理方法。常用的權函數有Huber法[10]、Hample法、Turkey法、Danish法、IGG方案[11]、IGGⅢ方案等。考慮Turkey權函數為有界連續函數；Danish法實質上為淘汰法，沒有抗差上的論證[11]；IGG法為有淘汰區的M估計，權因子變化平緩[12]，性能優于Huber法、Hample法[12-13]；IGG為跳躍函數，IGGⅢ權函數為連續函數。因此，本文選擇IGGⅢ方案[14]中的權函數用于加權最小二乘參數估計過程。該函數采用三段法進行權重定義，對正常段的觀測采用最小二乘估計，對可用觀測采用權因子降權，權因子取0～1之間的變值，對達到淘汰界的離群值進行剔除。權函數如下所示

(2)

將其繪制成圖直觀展示，如圖1所示。

將空間距離權重和觀測點可靠性權重同時納入地理加權回歸參數估計模型，模型表達為

(3)

式中，wij為空間距離權重，在地理加權回歸中常采用Gauss和Bi-square兩種核函數進行計算。由于不同核函數對模型參數估計的影響相差不大，最優帶寬的選取對參數估計結果影響較大[15]，因此，選擇最優帶寬值以確定合適的空間權重矩陣對模型解算至關重要。常用的帶寬選取方法有Akaike信息量準則(Akaike information criterion，AIC)、貝葉斯信息準則(Bayesian information criterion,BIC)及交叉驗證等方法，AIC準則和BIC準則通過極大似然估計計算，CV法采用二次誤差標準進行計算。

1.2 方法流程

方法流程如圖2所示，流程說明：

(1) 構建地理加權回歸模型。利用相關性分析和共線性分析選擇變量，并構建地理加權回歸模型。

(2) 計算最優帶寬。利用AIC準則、BIC準則、CV或ACV進行最優帶寬選取。

(3) 計算空間權重矩陣。根據最優帶寬，利用Gauss核函數、Bi-square核函數或自適應核函數計算空間權重矩陣。

(4) 估計回歸模型參數。構建地理加權回歸參數估計模型，根據最小化損失函數原則進行參數求解。

(5) 計算殘差。依據步驟(4)計算所得的參數值結果，計算因變量y的估計值。因變量觀測值與估計值的差值即為殘差。

(6) 計算評價指標。計算標準化殘差及MSE、MAE、R2等評價指標。

(7) 判斷是否存在離群值。通過標準化殘差判斷模型中是否存在離群值。若存在，利用IGGⅢ計算權因子，構建基于IGGⅢ的地理加權回歸模型，迭代進行模型求解，直到模型中不存在離群值時，結束迭代；若不存在，輸出結果。

2 試 驗

2.1 模擬數據試驗

2.1.1 數據生成

本文根據地理加權回歸模型特性設計模擬數據。其中，自變量和因變量滿足線性回歸關系，系數與采樣點空間位置有關，具體公式見表1。

表1 模擬數據生成公式

表1中，x1、x2為自變量，服從(0,1)均勻分布；u、v為位置變量，服從[0,20]均勻分布；ε為隨機誤差。此外，向模擬數據中添加高斯白噪聲。

2.1.2 對比試驗設置

本文將GWR、ACV-GWR和IGGⅢ-GWR進行對比試驗，采用Gauss核函數計算空間權重矩陣，GWR和IGGⅢ-GWR采用CV確定最優帶寬，ACV-GWR采用ACV確定最優帶寬。ACV計算方法為

(4)

2.1.3 試驗結果分析

利用模擬數據對以上3種方法分別試驗40次，表2列舉部分試驗結果。表3展示IGGⅢ-GWR較ACV-GWR、GWR各指標性能平均提升情況。

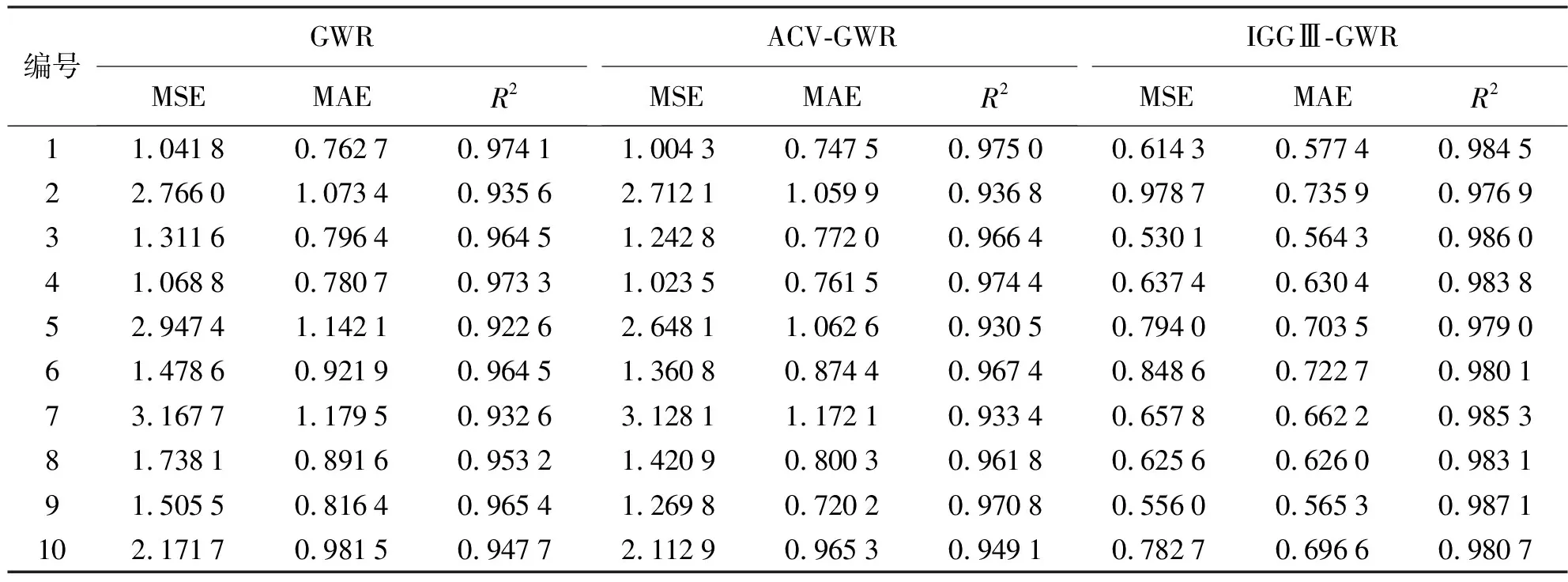
表2 部分試驗結果

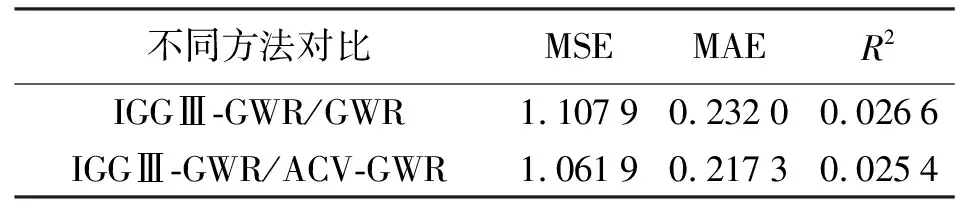
表3 各指標平均提升情況

從MSE、MAE、R2性能提升百分比來看，IGGⅢ-GWR比GWR性能分別提升51.14%、23.77%、28.4%，比ACV-GWR分別提升49.96%、22.57%、27.1%。

2.2 真實數據試驗

2.2.1 試驗數據

本文選用2016年1月至2018年3月北京地區空氣質量及其影響因素作為試驗數據進行分析驗證。計算CO、NO2、O3、PM10、PM2.5、SO2與空氣質量指數的Pearson相關系數(見表4)，CO、NO2、PM2.5、SO2與空氣質量指數顯著正相關，O3與空氣質量指數呈較強的負相關，PM10與空氣質量指數呈較強的正相關。

表4 各影響因素與AQI間的Pearson相關系數

對包含CO、NO2、O3、PM10、PM2.5、SO2在內的6種污染物進行多重共線性分析，以方差膨脹因子小于2且條件索引小于10為限定條件進行因子選取，最終選擇O3、PM2.5、SO2作為影響指標構建回歸模型。北京地區空氣質量監測站點分布如圖3所示。

2.2.2 試驗結果分析

分別采用GWR、ACV-GWR、IGGⅢ-GWR進行試驗，以MSE、MAE和R2作為指標對試驗結果進行評價,見表5。

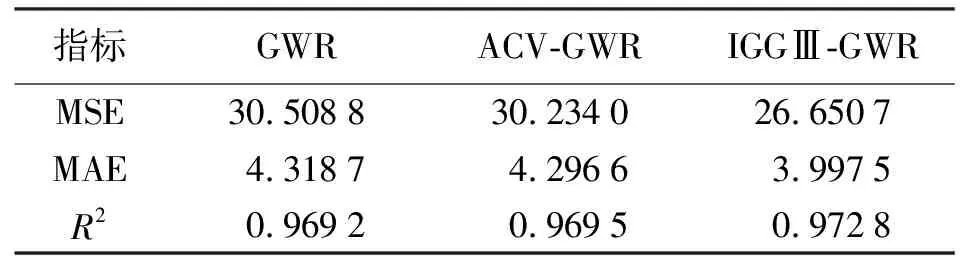
表5 真實數據試驗結果

從MSE、MAE、R2指標性能上看，IGGⅢ-GWR較GWR分別提升12.65%、7.44%、0.37%，較ACV-GWR分別提升11.85%、6.96%、0.34%。

隨機選取任意月份繪制空氣質量分布和標準化殘差分布，比較各模型結果，本文以2017年1月為例進行結果展示，如圖4—圖7所示。

圖4—圖7展示了空氣質量觀測值和不同模型估計結果。從圖4—圖7可以看出，2017年1月北京市空氣質量指數介于88～202之間，GWR估算結果介于29～150之間，ACV-GWR估算結果介于39～182之間，IGGⅢ-GWR估計結果介于87～208之間。從估算結果上看，IGGⅢ-GWR模型估算得到的空氣質量指數更符合真實情況。

從空氣狀況空間分布來看，2017年1月北京市南部地區空氣質量相對較差，GWR估計結果顯示中部地區空氣質量相對較差，ACV-GWR估計結果規律性不明顯，IGGⅢ-GWR估計得到的空氣質量空間分布情況與觀測值更吻合。

繪制不同回歸模型計算所得的標準化殘差分布，如圖8—圖10所示。

從圖8—圖10可以看出，GWR標準化殘差計算結果介于0～2.05之間，ACV-GWR標準化從殘差計算結果介于0～2.04之間，IGGⅢ-GWR標準化殘差計算結果介于0～1.98之間。從整體上講，IGGⅢ-GWR估計效果更好一些。從局部來看，IGGⅢ-GWR對北京中南部地區空氣質量估計效果優于其他兩種方法。

3 結 語

本文提出了基于IGGⅢ的地理加權回歸模型，將IGGⅢ方案應用于地理加權回歸，降低了離群值對參數估計的影響，提高了地理加權回歸模型對離群值的抵抗能力。通過模擬數據和真實數據與GWR、ACV-GWR進行對比試驗，以MSE、MAE、R2作為評價指標進行驗證。試驗結果表明，IGGⅢ-GWR可用于空間非平穩性表達與未知量預測，當數據中存在離群值時，基于IGGⅢ的地理加權回歸模型擬合效果更好。