一種基于GA-BP-MC神經網絡的高鐵橋墩沉降預測模型

馮紹權，花向紅，陶武勇，宣 偉，吳 偉，續 東

(1. 武漢大學測繪學院,湖北 武漢 430079； 2. 武漢大學災害監測和防治研究中心,湖北 武漢 430079； 3. 武漢理工大學土木工程與建筑學院，湖北 武漢 430070)

高速鐵路“以橋代路”的結構特性對橋墩設計提出了更高的要求[1]，為保障高鐵快速、平穩、安全運行，對橋墩進行沉降變形觀測尤為重要。目前針對沉降數據預測方法主要有灰色系統理論[2]、時間序列分析[3]、人工神經網絡[4-5]等。近年來，由于人工神經網絡算法具有自學習和處理非線性函數等優勢，廣泛應用于變形預測中，其中BP(back propagation)神經網絡算法應用最為普遍。然而BP神經網絡自身也存在缺陷，容易陷入局部極小值和收斂速度過慢[6]。

遺傳算法(genetic algorithm,GA)具有很強全局搜索能力[7]，是一種全局優化算法。馬爾科夫鏈由于不受過去狀態影響，具有無后效性[8]，對多因素影響系統預測具有一定的優越性。本文結合馬爾科夫鏈(Markov chain,MC)和遺傳算法優化BP神經網絡，提出一種適合高鐵橋墩沉降預GA-BP-MC神經網絡預測新方法，并將本文方法應用于工程實例，通過與BP神經網絡、GA-BP神經網絡預測模型對比分析，驗證本文方法的有效性和可行性。

1 GA-BP神經網絡模型

1.1 BP神經網絡原理

BP神經網絡最早用于研究非線性連續函數[9]，其結構簡單、易操作，是目前應用最多的人工神經網絡之一[10]，它包含輸入層、輸出層和一層或多層隱含層，利用誤差反向傳播調整多層前饋神經網絡的權重，改進輸入層和輸出層的非線性映射關系[11]。BP神經網絡具有自學習、自適應、分布式存儲等特點，目前已被廣泛應用于非線性預測[12-13]。

1.2 遺傳算法優化BP神經網絡結構

遺傳算法是一種基于自然選擇和遺傳理論的隨機優化算法，通過選擇、交叉和變異等操作對所有個體進行篩選，根據適應度值保留優秀個體，淘汰適應度差的個體[14]。遺傳算法優化過程[15-17]主要包括編碼、確定適應度函數、選擇操作、交叉操作、變異操作5個方面，具有很強的全局尋優能力。

BP神經網絡是按照梯度下降的方法求取誤差函數最小值的過程，對初始權值等網絡參數十分敏感，全局搜索能力較差，易陷入局部最優，本質是一種局部優化方法；遺傳算法優化網絡結構時不依賴于梯度，采用選擇、交叉和變異操作進行搜索，具有很強的全局搜索能力。用遺傳算法優化BP神經網絡結構可以結合二者的優勢，彌補BP神經網絡的缺陷，其基本原理是發揮遺傳算法的全局搜索能力，優化網絡的初始權值和閾值，使其搜索范圍縮小至全局最優附近，隨后利用神經網絡非線性逼近能力，達到快速收斂的效果。

2 GA-BP-MC神經網絡模型

2.1 MC預測值修正模型

馬爾科夫鏈是一種無后效性隨機過程，可根據系統當前時刻狀態推求下一時刻的狀態概率分布，從而確定下一時刻狀態[18]。時間序列統計量多數都具備馬爾科夫鏈特性，利用這種特性可以進一步提高模型的預測精度。利用馬爾科夫鏈修正GA-BP神經網絡模型具體步驟如下：

(1) 狀態劃分：根據GA-BP神經網絡模型預測值的相對誤差大小和分布密度，采用最值均方差法將相對誤差區間分成n個狀態[18]，即S=(S1,S2,…,Sn)。其中n的計算方法為

n=EVEN(d/σ)

(1)

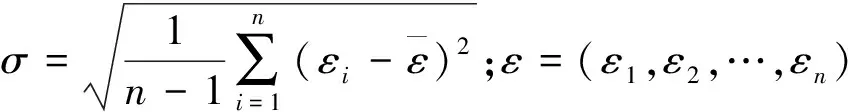
(2) 狀態轉移概率矩陣[19]：相對誤差Si經k時步狀態轉移到狀態Sj的概率為

(2)

式中，Mij(k)是Si經k時步狀態轉移到狀態Sj的次數；Mi是相對誤差在狀態Si出現的次數。

進行系統預測一般只需考慮1時步狀態轉移矩陣，即

(3)

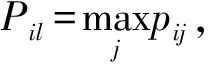
蓮心堿對佛波酯所致耳腫脹炎癥模型小鼠的抗炎作用及機制研究 ………………………………………… 姚 茹等（17）：2364

(3) 預測值修正：本文取預測的相對誤差狀態所處區間中點為預測值的相對誤差[20]，預測值修正值為

(4)

式中，ΔD、ΔU分別為預測的相對誤差所處狀態區間的上下限值；f(x)為GA-BP神經網絡的預測值。

2.2 GA-BP-MC神經網絡模型構建

本文結合馬爾科夫鏈理論和遺傳算法優化BP神經網絡模型主要過程為：首先初始化神經網絡結構；然后用遺傳算法優化的網絡初始權值和閾值訓練并保存神經網絡；最后結合MC模型修正GA-BP神經網絡模型預測值，具體過程如圖1所示。

3 高鐵沉降預測實例

3.1 試驗數據

高速鐵路建設和運營過程中，為保障列車安全、平穩高速運行，對高鐵橋墩進行定期監測具有十分重要的意義。本文對某城際鐵路某橋墩20期定期沉降監測數據[1]進行預測，實測累計沉降值見表1。

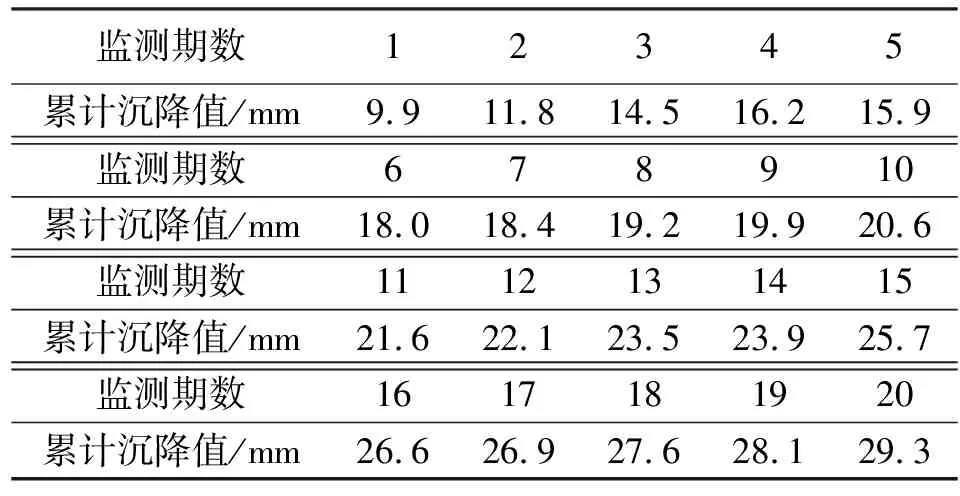
表1 監測點實測累計沉降值

3.2 試驗與結果

本文結合GA-BP-MC神經網絡預測模型，利用前17期數據滾動式[21]預測后3期數據。以第1—5期實測累計沉降數據為網絡輸入，第6期數據為網絡輸出；類推至以第12—16期數據為網絡輸入，第17期數據作為網絡輸出，組成網絡訓練樣本。用訓練好的GA-BP神經網絡預測后3期的數據，將所得的預測值用MC模型進行修正，得到GA-BP-MC網絡預測值，分析優化后GA-BP-MC神經網絡預測模型精度。預測精度評定指標有絕對誤差(absolute error)、誤差絕對值均值(mean absolute error,MAE)、平均絕對百分誤差(mean absolute percentage error,MAPE)、誤差均方差(mean squared error,MSE)。

為加快網絡訓練速度，將實測累計沉降數據進行歸一化處理。利用基于L-M優化算法的BP神經網絡反復訓練和對比，當隱含層神經元數目為8時，網絡擬合效果最好。

為了驗證本文算法的可行性和有效性，選擇與BP神經網絡模型和GA-BP神經網絡模型結果進行對比。3種網絡模型的網絡訓練次數均為1000次，目標誤差均為0.000 1，學習速率均為0.05，并設定遺傳算法種群規模為50，遺傳代數為100，變異概率為0.05，交叉概率為0.6，選擇概率為0.08。

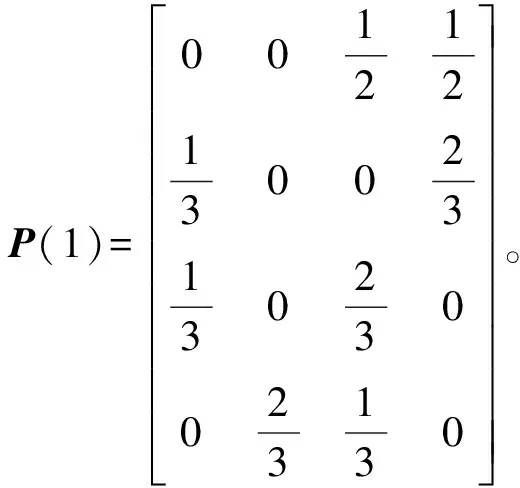
監測期數實際累計沉降值/mmGA-BP神經網絡擬合值/mm相對誤差/(%)狀態劃分S1S2S3S419.9——————211.8——————314.5——————416.2——————515.9——————61818.1331-0.7394√718.418.35470.2462√819.219.19630.0193√919.919.87600.1206√1020.620.6212-0.1029√1121.621.7178-0.5454√1222.122.04120.2661√1323.523.6009-0.4294√1423.923.84020.2502√1525.725.7732-0.2848√1626.626.45330.5515√1726.926.85340.1732√

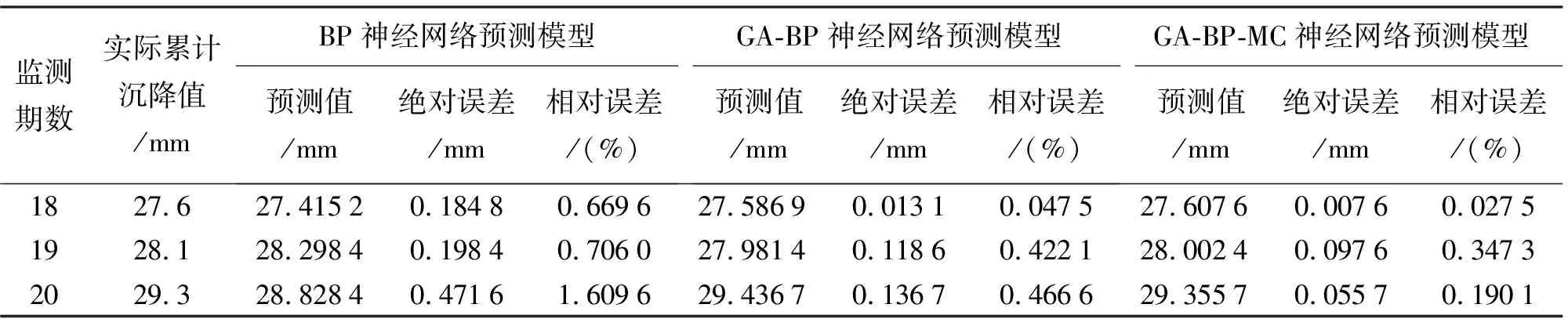
表3 累計沉降預測值比較

圖3為各模型累計沉降預測值。由圖3定性分析可知，GA-BP-MC神經網絡模型3期預測值與實際累計沉降值接近，預測效果比其他兩種好。從表3定量分析可知，GA-BP神經網絡預測模型的絕對誤差較傳統BP神經網絡預測模型最大優化值為0.334 9 mm，可見遺傳算法可以提高BP神經網絡預測模型精度；本文基于MC理論繼續優化GA-BP神經網絡模型，最小絕對誤差達到0.007 6 mm，在GA-BP神經網絡模型的基礎上預測精度得到進一步提升。

為進一步分析本文所建模型預測精度，分別計算各預測模型的MAE、MAPE、MSE，見表4。由表4可知，GA-BP-MC神經網絡預測模型較GA-BP神經網絡預測模型在MAE、MAPE、MSE 3項精度指標上分別提高了40.11%、39.65%、37.98%，較傳統BP神經網絡預測模型分別提高了81.19%、81.08%、79.31%。綜合分析3種神經網絡預測模型，可見遺傳算法全局尋優能力提高了傳統BP神經網絡預測模型精度，結合MC理論根據訓練數據相對誤差的轉移概率矩陣確定預測值相對誤差狀態，可進一步提高了預測值精度，驗證了本文算法的有效性。

4 結 語

為了建立適合高鐵橋墩沉降預測模型，本文結合馬爾科夫鏈和遺傳算法理論優化BP神經網絡，建立了GA-BP-MC神經網絡預測模型，通過實際工程數據分別與BP神經網絡預測模型和GA-BP神經網絡預測模型進行對比分析，結果表明了本文預測模型精度更高，驗證了GA-BP-MC神經網絡沉降預測模型的有效性和可行性。

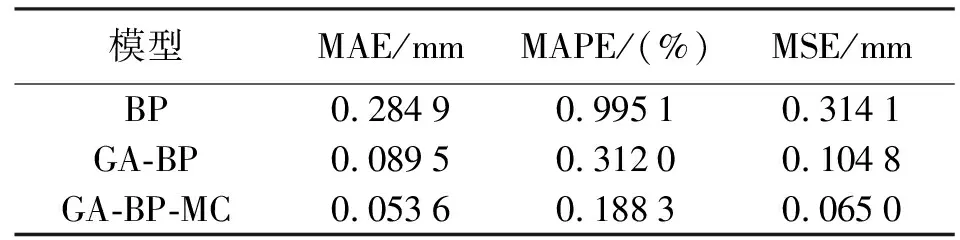
表4 各預測模型預測精度比較