基于改進DE算法的PID參數整定

王劍平

（浙江省能源集團有限公司，浙江 義烏 071003）

0 引言

PID 控制器結構簡單，魯棒性強，適用性強，在實踐過程中易于理解和實施。因此，到目前為止，仍舊是工業過程中使用最為廣泛的控制器。但是PID 控制器的缺點也十分明顯，就是控制性能十分依賴于PID 控制器參數的整定與優化，PID 參數的優劣直接影響到系統的控制性能。因此，如何尋找更為優秀的PID 控制器參數至關重要。

在實際生產過程中，絕大多數的PID 控制器參數仍采用工程整定方法[1]，諸如經驗整定法，以Ziegler-Nichols(Z-N)法為代表的基于規則的方法、內模控制等控制方法。這些方法雖然理論基礎比較低，也很容易實現，經驗比較豐富的技術人員可以得到不錯的控制效果，但是由于現階段工業過程的復雜工況所致，傳統的PID 參數整定方法已經逐漸跟不上控制過程的需要。隨著控制領域的迅速發展，現在也已經提出了許多基于人工智能技術的新型算法，例如Krohling[2]提出了遺傳算法，Azwar[3]提出的神經網絡算法等。這些算法具有很廣泛的應用前景，并且在優化問題上有獨到的優勢，但是應用到實際生產過程中并不能夠獲得預期的效果。其中一個很重要的原因就是大多數調整方法都是針對特定的生產過程和生產環境而產生的，它們僅在自己的領域中才可以得到最理想的結果。不確定應該選用哪種整定方法可以為給定的生產過程提供良好的控制。因此，如果存在一種普遍線性過程的高性能通用設計方法來獲得不錯的控制效果，是十分有利的。

差分進化法（Differential Evolution, DE）是Rainer Storn和Kenneth Price[4]在1995 年為求解切比雪夫多項式而提出的一種基于群體差異的啟發式隨機搜索算法。其本質上是一種“貪婪算法”，相比于一般的進化優化算法，DE 算法從一個群體的多個點協同搜索，這是DE 算法能夠很好地避免陷入局部最優解，同時具有記憶功能可以跟蹤當前搜索情況以調整其搜索策略，具有較強的全局收斂能力和魯棒性，比遺傳算法要優秀許多。但是標準DE 算法也存在只針對連續域、收斂速度慢等問題。

許多專家學者在此基礎上進行了改進，如王艷宜[5]提出了一種混合差分策略，將兩種差分策略并行混合作用于種群中，潘暉[6]等提出了一種改進的二進制差分進化（Modified Binary Differential Evolution, MBDE）算法，并采用MBDE 與PID 控制器參數穩定域結合，在可行域范圍內求得最優解，常俊林[7]等提出了一種隨機縮放因子來增強搜索能力。如何進一步提高DE 算法的收斂速度與性能，優化控制器參數上仍舊有許多工作要做。

本文為了提高PID 參數的優化速度，并且在不降低控制性能，破壞全局最優約束條件的情況下，在基于以上研究的基礎上，改進了DE 算法的參數設置，設計了新的最優目標函數應用到PID 參數的整定，并進行了實例仿真。

1 標準DE算法

DE 算法是一種基于種群的優化器，通過對目標函數在多個隨機選擇的起始點進行抽樣，進行智能指導優化搜索。DE 算法根據父代個體間的差分矢量通過變異、交叉和選擇3 個操作來進行智能搜索。DE 算法基本思想是在預定區間內，選取隨機初始群體的任意兩個個體的向量差進行加權，在與通過確定的規則與另外一個個體求和以產生新的個體，然后將新個體與正在搜索的種群中提前選定的個體（一般為第一個個體）進行比較，保留經過取優函數篩選之后更優的個體，通過預定次數的迭代運算，優勝劣汰，不斷地搜索逼近最優解。

1.1 生成初始種群

確定初始種群的向量個體界定范圍[L,H]，隨機生成n個N 維向量，其中第k 個個體xi,j(k)

所有n 個N 維隨機向量，組成初始種群

其中，k=1,2,…n--種群內第k 個個體；

randj(0,1)--[0,1]之間的隨機小數；

Uj，Lj--第k 個個體的上界和下界。

1.2 變異操作

對以上生成的初始化種群，通過變異和重組后得到一個由n 個向量構成的種群，DE 算法中的變異操作是將一個可縮放的、隨機選取的向量差分增量與第3 個向量按照特定規律進行組合，生成一個新的變異向量vi,j。常用的變異操作類型有以下5 種方式[8]：

a）DE/rand/1

b）DE/rand/2

c）DE/best/1

d）DE/best/2

e）DE/current-to-best/1

其中，g=0,1,…,G—所屬代數；

r1,…,r5?N—從g代種群中隨機選取的互不相同的整數；

xbest,j--g 代種群中最符合取優函數數值的個體；

F—DE 的變異因子。

變異操作是DE 算法的關鍵，一般在5 種方式中隨機選取一種，但是也可以采用類似文獻[9]組合的方式進行變異。

1.3 交叉操作

為了完善DE 算法的變異搜索策略，增加種群的多樣性，DE 算法使用了“均勻交叉”方法，也被稱為“離散重組”。交叉操作利用從兩個不同的向量中復制的參數值來構造試驗向量，然后將每一個種群中的向量與一個變異向量進行交叉操作：

其中，CR?[0,1] —交叉因子；

jrand—區間[1,N]選取的隨機數，保證hi,j,g不完全復制xi,j,g，從而避免種群的無效雜交。

1.4 選擇操作

如果實驗向量hi,j,g的適應度值小于等于目標向量xi,j,g的適應度值，則保留試驗向量到下一代中，作為下一代的目標向量；否則，目標向量就會保持，繼續作為下一代種群的目標向量[10]。選擇操作表示為：

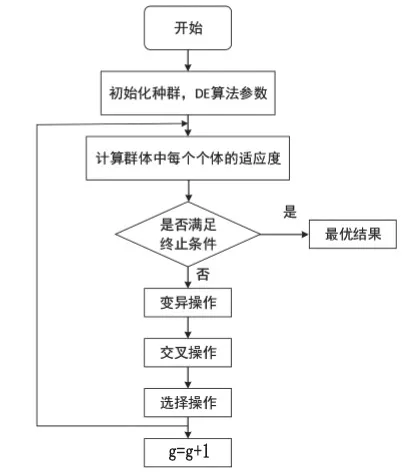
圖1 差分進化法流程圖Fig.1 Differential evolution method flow chart

其中，f(xi,j,g)—計算出的第g 代個體xi,j,g適應度目標函數值。

DE 的選擇算子是依次對試驗向量進行運算，然后與目標向量作比較，保留最優的向量，使得子代個體的適應度值總是優于父代個體的適應度值，從而逐步向最優向量逼近，得到滿意解。

綜上所述，差分進化算法的基本流程如圖1 所示。

2 改進DE算法的參數設置

DE 算法作為一種非常實用且有效的優化算法，但標準DE 算法也會陷于局部最優解，容易出現早熟收斂等現象。針對DE 算法的這些問題，提出了新的檢索因子。

2.1 線性調整變異因子F

變異因子F 是DE 算法的關鍵參數，它表征種群的多樣性和收斂性。DE 算法中F 一般都取定常數，F 值較小時，群體的差異度減小，進化過程比較不容易跳出局部極值導致種群過早的收斂；F 值較大時，收斂速度會減小，但是容易跳出局部極值。經查閱多數文獻，變異因子F 的取值在區間[0,2]內，一般在1 的附近選取。

本文中設計了一種線性調整變異因子：

其中，Fmax—選定變異因子最大值；其中，

Fmin—選定變異因子最小值；

g—當前進化代數；

G—最大進化代數。

在DE 算法運行的初期，F 取值較大，有利于拓展搜索空間，保持種群的多樣性；在算法后期，收斂的情況下，F取值較小，更有利于選中最佳區域，逼近最優取值，提高收斂速率和搜索精度。

2.2 修補算子

在變異操作中，針對不同問題，變異后的向量個體有可能在搜索空間以外。因此，對DE 算法進行修補操作，常用的修補算子為：

2.3 線性調整交叉因子CR

交叉因子CR 表征個體參數的各維對交叉的參與程度，全局與局部的搜索平衡能力。標準DE 算法中CR 一般都取定常數，CR 值較小時，種群多樣性會減小容易過早陷入局部最優解；F 值較大時，又會因為擾動大于群體差異度而導致收斂緩慢，無法得到最優解。交叉因子是把變異向量的某些分量復制到實驗向量中，是用戶自行選取的數值，根據文獻一般選在0.6 ～0.9 之間。

本文設計了一種線性調整交叉因子：

其中，CRmax—選定交叉因子最大值；

CRmin—選定交叉因子最小值。

2.4 目標函數

通常情況下，為了獲取滿意的過渡過程動態特性，采用誤差絕對積分性能指標作為參數選擇的最小目標函數。本文中為了防止控制量過大，就選用誤差絕對時間積分性能指標和控制輸入平方加權結合作為參數選取的最優指標函數：

其中，c1?[0,1]—權值；

e(t)—系統誤差；

u(t)—控制其輸出。

3 仿真實例

考慮如下被控對象：

采樣時間為1s，輸入指令為yr=1(t)，利用DE 算法對PI 參數整定，采用如下參數設置：

樣本個數n=50；

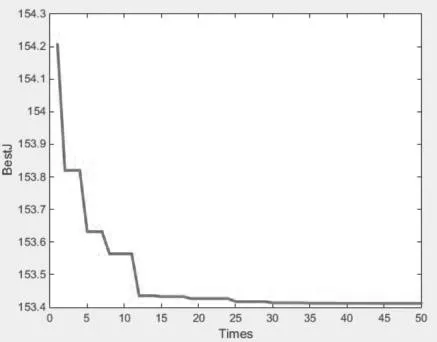
圖2 標準DE 算法Q的優化過程Fig.2 The optimization process of Q in the standard DE algorithm

圖3 文獻[6]算法Q的優化過程Fig.3 The optimization process of Q in the algorithm of literature [6]

圖4 文獻[1]算法Q的優化過程Fig.4 The optimization process of Q in the algorithm of literature [1]

圖5 本文中目標函數Q的優化過程Fig.5 Optimization process of the objective function Q in this paper

表1 不同文獻中最優目標函數Q值Table 1 Q value of optimal objective function in different literatures

Fmax=1.2；Fmin=0.3；

CRmax=1.2；CRmin=0.3；

c1=0.999；

G=50；

kp?[0,1]，ki?[90,100]；

經過相應代數的進化，PI 參數的整定結果為kp=0.6572,ki=91.3724；最優性能指標Q=148.5321。

在選用相同的被控對象，設置相同的優化參數情況下，表1 顯示了不同文獻中的最優目標函數值，圖2 ～圖5 顯示了不同文獻中的目標函數優化過程。

圖6 整定后階躍響應曲線Fig.6 Step response curve after tuning

目標函數的整定過程已經整定后的階躍響應曲線如圖6 所示。

從仿真結果對比可以看出，DE 算法參數整定的PID 控制器的綜合控制性能相比較于其它算法要好上許多，過渡過程也比較平滑，調節時間也有了明顯的優化。證明了DE算法可以獲得更加良好控制性能的PID 控制器的參數，優于傳統的整定方法。

4 總結

PID 參數整定是設計PID 控制器的關鍵。本文對標準DE 算法的參數設置進行了優化設計，在搜索過程中對縮放因子，交叉因子進行線性化調整，采用了新的最優性能指標。經過仿真驗證，也證實了DE 算法更有效，魯棒性更好，可以準確地找到全局最優點，并且決策變量很少，不僅僅是PID 參數整定，在其他方面也具有非常廣泛的作用。

DE 算法是一種有效的取優算法，但是也具有一定的局限性，比如初值的隨機性就限制了其應用。而且，DE 算法只能取優，因此對于PID 控制器參數的設計無能為力。下一步的研究方向可以將DE 算法引入到更加有效的理論控制器參數整定中，以獲得更加精確的參數，獲得更好的控制性能。