常微分方程與代數方程的聯系

新疆喀什大學 阿依古再麗·伊斯馬伊力

常微分方程和代數方程都屬于方程的一種，方程所共有的屬性也意味著這兩種方程中存在相定的關系。通過加強常微分方程和代數方程之間的聯系，不僅可以掌握微分方程理論本身，還可以更充分地了解代數方程。

一、代數方程的基礎作用

1．代數因式分解與常微分方程算子解法

因式分解是將代數方程分解為線性微分方程的一種有效手段。

例1 常系數線性微分方程的分析y’’+py’q=f（x） ①

D2+pD+qI[y]=f（x） （微分算子單位I[y]=D"[y]=y） ②

這時,若存在常數α和β，使多項式f（D）可以滿足：f（D）=D2+pD+qI[y]=（D-I）（D-1）。

那么方程②是：（D-I）（D-1） [y]=f（x）。這時，令（D-1）[y]=u（x）。則：

（D-I） [u（x）]=f（x） ③

方程③的解為u=eax[f（x）e-axdx+C1], 那么（D-1） [y]=eax[f（x）e-axdx+C1]，因此，y=eβx[e（a-βx）（f（x）e-axdx+C1）dx+C2。

（1）若α≠β，則

（2）若α=β，則

例1的解法則為微分算子解法，它令微分方程的解與代數方程的解形成有機的聯系，微分方程階數的約簡與代數方程的因式分解是相同的。

2．切線意義與常微分方程幾何解法

常微分方程的解是以積分的形式得到的，但常微分方程中由于較多不可積函數的存在而經常不可解，這將使得本文通過定性分析對常微分方程進行研究。

二、常微分方程的指導作用

1．線性微分方程解的構造與數列通項公式

推出方程①的疊加原理：如果y*是方程①的一個特解，是方程②的通解，那么方程①則有通解為：

根據常系數線性微分方程：

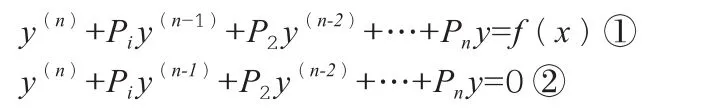
將常微分方程的疊加原理推廣到遞推序列中，得到了相應的結論。

對于遞歸數列，其遞歸方程bn+k+p1an+k-1+…+pkan=f（n）（pi為常數,i=1,2,。。。,k）③，對應的齊次方程是bn+k+p1an+k-1+…+pkan=0④。

若方程④的通解是方程③的一個特解，則方程③有通解是bn=+bn*。

該方法采用常系數線性微分方程解的構造方法，通過類比建立了遞推序列解的理論，這是代數中常見的同構關系。例如，代數中的對偶也能夠作為同構應用的結果。所以，常微分方程的數學思想與方法能夠對代數方程起著關鍵的指導作用。

2．切線意義與常微分方程幾何解法

常微分方程的解是以積分的形式得到的，但常微分方程中由于較多不可積函數的存在而經常不可解，這將使得本文通過定性分析對常微分方程進行研究。

二、常微分方程的指導作用

1．線性微分方程解的構造與數列通項公式

推出方程①的疊加原理：如果y*是方程①的一個特解，是方程②的通解，那么方程①則有通解為：

根據常系數線性微分方程：

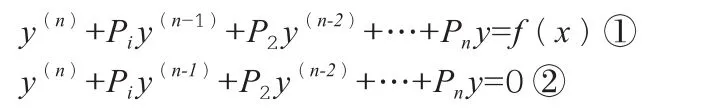
將常微分方程的疊加原理推廣到遞推序列中，得到了相應的結論。

對于遞歸數列，其遞歸方程bn+k+p1an+k-1+…+pkan=f（n）（pi為常數,i=1,2,。。。,k）③，對應的齊次方程是bn+k+p1an+k-1+…+pkan=0④。

若方程④的通解是方程③的一個特解，則方程③有通解是bn=+bn*。

該方法采用常系數線性微分方程解的構造方法，通過類比建立了遞推序列解的理論，這是代數中常見的同構關系。例如，代數中的對偶也能夠作為同構應用的結果。所以，常微分方程的數學思想與方法能夠對代數方程起著關鍵的指導作用。

2．Gauchy問題與Euler三角公式

三角函數作為代數方程的重要組成部分，可以統一為在復數范圍內的函數形式。

例3 三角公式證明：

sin（α+β）=sinαcosβ+cosαsinβ；

cos（α+β）=sinαsinβ+cosαcosβ。

例3 三角公式證明：

sin（α+β）=sinαcosβ+cosαsinβ；

cos（α+β）=sinαsinβ+cosαcosβ。

解：方程x"+x=0有特解：r=sinu和cosu,那么通解則為：令另令u=α+β, 那么

因此，該三角公式獲得證明。

常微分方程和代數方程屬于一類方程，它們相互聯系。一方面，代數方程在常微分方程的分析中有著基礎性的作用。另一方面，常微分方程又指導著代數方程。常微分方程和代數方程的這種相互作用令數學研究提供了高效便捷的方法。