數學思維形成的助推器
韓潤柏
摘要:數學教學的魂就是培養學生的數學思維,只有把學生的數學思維培養好了,才能讓學生在數學方面有發展的潛力和前景,對于數學教學來說,一堂課無非導學練測四大環節,為了抓住課堂教學這塊主陣地,我們只有精心設計課堂教學中的"導學練測",有意識的培養學生的數學思維,這樣才有益于學生的長遠發展。
關鍵字:數學思維;導學練測;長遠發展
中圖分類號:G421文獻標識碼:A文章編號:1992-7711(2019)12-107-1
在數學課堂教學中,數學思維的培養是數學教學的核心任務。我們在平時的教學中不應讓學生在課堂學習中圍著老師和書本轉,或者鉆入題海大戰而不能自拔;甚至有的學生對所學知識一知半解,只會照貓畫虎的解題,而不了解解題的真正的道理或依據是什么?這樣學生的數學思維就得不到培養和訓練,導致他的思維僵化,懶惰進而閉塞。照這樣長此以往,數學教學質量可想而知,即便學生在某一段出現好的學習成績,也是曇花一現。綜上種種原因,我們就有必要以數學教學的魂引領我們的教學設計。
一、"導"是一節課的開端,要有疑性
"導":是一堂課的起始環節,授課教師要靈活多樣,根據所授內容和學生實際水平,通過現代的教學輔助工具,巧妙地利用社會熱點問題、學生的生活體驗、生產實際等創設情境,導入新課。一節課一個好的導入,能喚醒學生積極思考的神經,這對一堂數學課的成效有著舉足輕重的功效。我認為一些較好的導入新課的方法有:①創設問題情景導入。比如在學習北師大版八年級數學上冊《一定是直角三角形嗎》那節課時,我就設計了兩個問題情境A.直角三角形中,三邊長度滿足什么樣的關系?B.如果一個三角形中有兩邊的平方和等于第三邊的平方,那么這個三角形是否就是直角三角形呢?這樣學生帶著疑問自然而然就要辯證的去思考,無形中可以培養學生的思維能力。②以生活實際例子導入新課。比如在學習北師大版八年級數學上冊《認識二元一次方程組》那節課時,我創設了這樣的情境,昨天,有8人去黃山公園玩,他們買門票共花了34元,每張成人票5元,每張兒童票3元,那么他們到底去了幾個成人?幾個兒童?在導入時設計一些學生常見的事例,能激發學生學習的積極性,并在此問題中可以引導學生一題多解,無形中就培養了學生的發散思維。
二、"學"是一堂課的中心工作,在學中要以學生的思維培養為核心
1.在探究活動中有意培養學生研究性思維
現在的數學課程的設置每節課都有探究活動,授課教師可以靈活整合教材資源,在探究問題的設計上要下一番功夫,所涉及的活動要有利于學生研究新思維的形成。如:在北師大版九年級
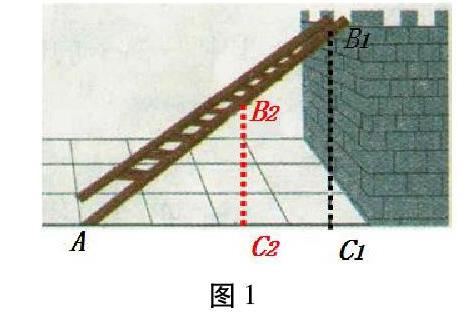
數學下冊《銳角三角函數》第一課時探究銳角正切值與直角三角形的大小無關時,我設計的探究活動是:安源想通過測量B1C1及AC1,算出它們的比來說明梯子的傾斜程度;卻因身高原因不能直接測量梯子頂端到墻腳的距離B1C1,進而無法說明梯子的傾斜程度,他該怎么辦(圖1)?你有什么錦囊妙計?學生通過探究推理自然而然就能理解銳角的正切值與直角三角形的大小無關。
2.在學中巧妙利用認知沖突,促就思維的形成
比如在用公式法解二元一次方程的教學中,當學生配方后在開方時,就遇到了現學的公式與以前的二次根號下非負的矛盾,這樣就促使他們去研究,去思考,通過他們自己在認知過程中發現矛盾,進而解決矛盾的過程,就能加深學生對所學知識的認識和理解。教學中通過一次次的解決認知上的沖突,進而達到培養數學思維的目的。
三、"練"是數學教學中的重要組成部分,以練促思維的養成
練的過程可以反饋一些有用的信息,比如學生對知識的掌握程度,也可以發展學生的創新意識,提高學生的計算技能,所以我們一定要在練的環節上下功夫。我們在設計練習題時,既要考慮基礎知識,又要考慮題型的層次性,要讓不同的學生得到不同的發展。另外,所涉及的題型要有開放性的題,這樣就有助于學生創新思維的形成。比如在上反比例函數的圖像與性質時,設計的課堂練習題其中有一道是這樣的,反比例函數y=(k-2)/x,在每個象限內y都隨著x的增大而增大,這是一道開放性的題,極易培養學生的創造性思維。這樣在課堂教學中設計合理的練習,就可達到練中培養數學思維的目的。
四、"測"是教學中練之后的提升過程,在提升中養思維
在教學中進行當堂測驗不但可以反饋教與學中存在的不足,還可以在測中提升學生的能力和數學思維,測有時可以代替練,在測中雙方的能力和思維都可以得到提升。但是,我們要把測的中心工作放在提升學生能力,掌握基礎知識和基本技能上,不能只是簡單的測。
學生數學思維的培養不是一朝一夕之功,貴在堅持和有心,我們要在平時的點滴工作中做個有心人,抓住課堂教學中的主要環節,精心設計每個環節,讓學生的數學思維在"導學練測"中得到應有的培養,這樣學生在數學方面才有長遠的發展前景。
[參考文獻]
[1]錢學森(編).關于思維科學[M].上海:上海人發出版社,1986.
[2]孔慧英,梅智超(編).現代數學思想概論[M].北京:中國科學技術出版社,1993.
[3]朱智賢,林崇德(編).思維發展心理[M].北京師范大學出版社,1990.
[4]郭思樂,喻偉(編).數學思維教育論[M].上海:上海教育出版社,1997.
[5]席振偉(編).數學的思維方式[M].南京:江蘇教育出版社,1995.
本文為甘肅省教育科學規劃"十三五"研究成果(課題批準號:GS[2018]GHB2136)。

