海上風電機組大直徑嵌巖單樁基礎結構設計關鍵參數的研究
上海勘測設計研究院有限公司 ■ 校建東 林毅峰
0 引言
單樁基礎因其結構形式簡單、施工技術成熟,在國內外海上風電場中均得到了廣泛應用。目前我國已建成的單樁基礎風電項目大部分位于江蘇沿海地區,這些地區的地基為軟基。然而,福建、大連、廣東、廣西的沿海地區存在大面積的淺覆蓋層和裸巖地層,在這些地區建設海上風電場,其基礎若采用樁基礎則必然面臨樁基嵌巖的問題。
彈模E是衡量巖石抵抗彈性變形能力的重要參數,而巖層的彈模E在樁基嵌巖問題研究中尤其重要,不同巖層、不同性狀的巖石決定了其E值大小的不同,且直接對單樁變形、嵌巖設計有顯著影響。本文采用廣義H-B 強度準則及地質強度指標GSI 來確定福建某風電場的巖石參數,并通過Z-SOIL 有限元軟件分析了樁基嵌巖設計中巖石的彈模、嵌巖單樁基礎入巖深度及鋼管樁樁身壁厚這3 個關鍵參數對樁身承載能力的影響。
1 H-B強度準則及地質強度指標GSI
1980年,Hoek 和 Brown[1-2]通過對幾百組巖石的三軸試驗資料和大量現場巖石試驗成果進行統計分析,并結合巖石性狀方面的理論研究成果和實踐檢驗,推導出了巖石破壞時主應力間的關系式,即Hoek-Brown(H-B)強度準則。其表達式為:
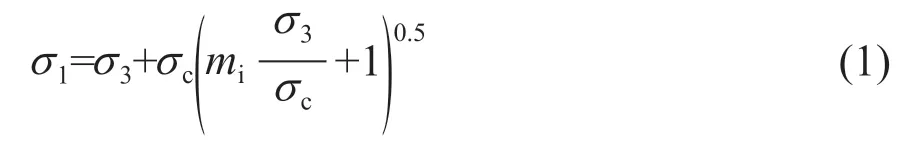
式中,σ1為最大壓應力,MPa;σ3為最小壓應力,MPa;σc為巖石單軸抗壓強度,MPa;mi為巖石經驗參數,反映巖石的軟硬程度。
對于巖石經驗參數mi的取值,Hoek 和工程地質專業技術人員結合了大量的實驗和工程經驗,提出了一個比較詳細的取值方法,如表1所示[3-4]。
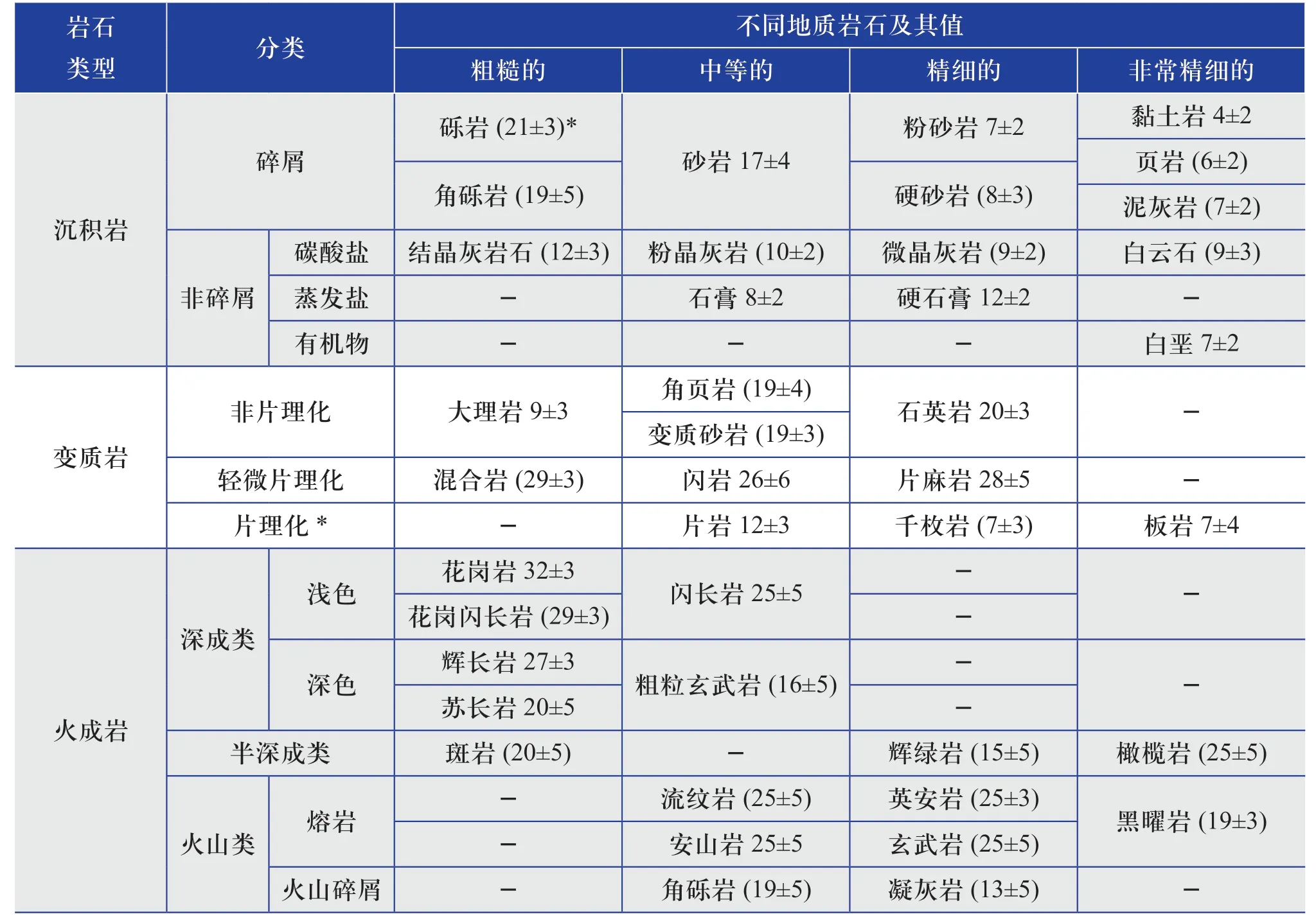
表1 巖石經驗參數mi 的取值
雖然最初的H-B 強度準則有很多優點,但其也存在一些不足,比如,未考慮不同巖體的強度參數、對于各向異性明顯的節理巖石適用性差等[5]。于是在 1992年,Hoek 等[6]對 H-B 強度準則進行了改進,使其可同時應用于巖石和巖體,稱之為“廣義H-B 強度準則”,其表達式為:

式中,mb為無量綱參數;a為經驗參數;s為反映巖體破碎程度的無量綱參數,取值范圍為0~1.0,對于完整巖體,s取1.0。
廣義H-B 強度準則在原準則基礎上引入了巖體參數mb、s、a,以適用于低應力條件下質量較差的巖體。
如何選取準確的巖體參數是廣義H-B 強度準則在工程應用中的關鍵。1994年,Hoek[7]提出了基于地質強度指標GSI 的巖體參數mb、s和a的取值方法為:
1)對于質量較好的巖體 (GSI>25),mb、s和a可表示為:
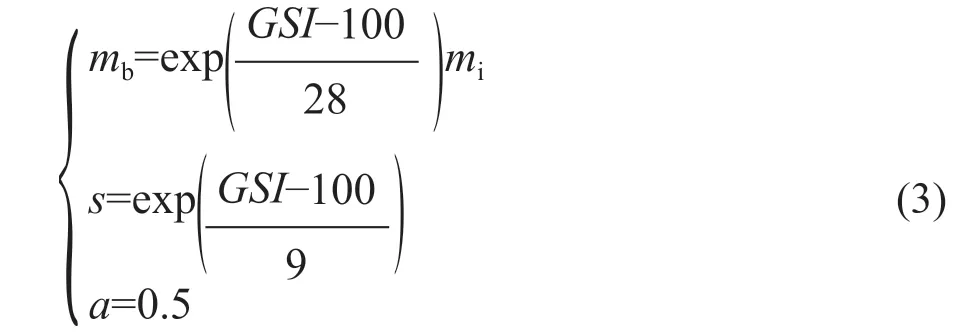
2)對于非常破碎的巖體 (GSI<25),mb、s和a可表示為:
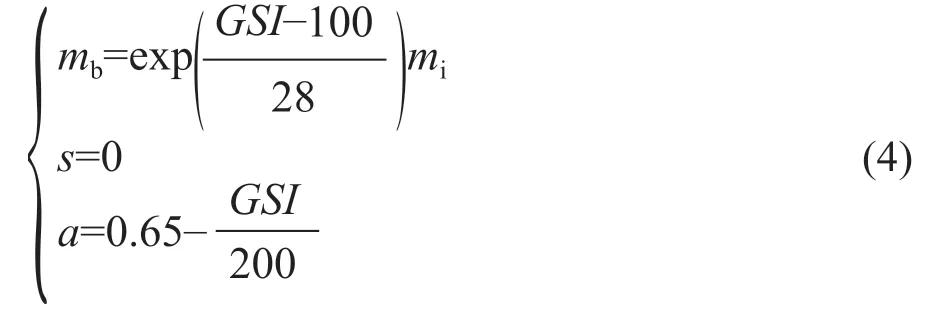
2002年,Hoek 等[8]引入了一個可考慮爆破影響力和應力釋放的擾動影響因素D(取值范圍為0~1.0,巖體無擾動時為0,非常擾動時為1.0),提出了基于GSI的巖體參數mb、s和a的取值方法為:
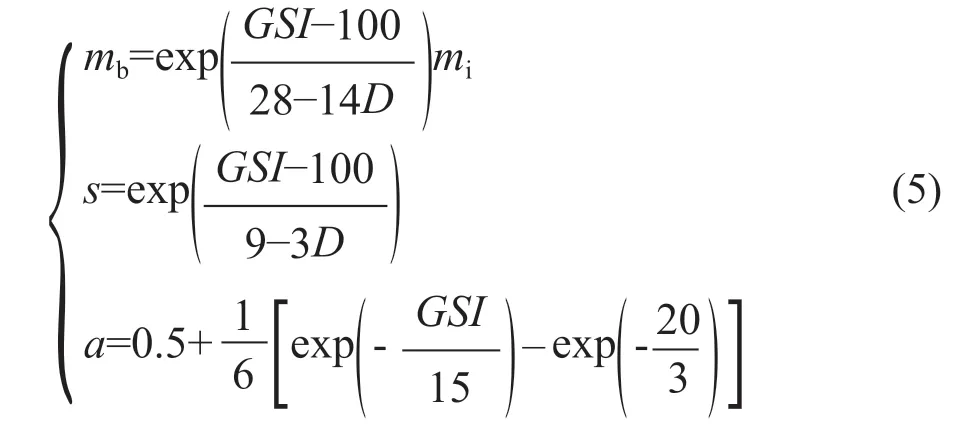
1999年,Sonmez 等[9]提出了較為詳細的GSI定量評價方法,考慮到了不連續面分布體積率、粗糙度、風化程度和填充物性質等方面,可通過插值查地質強度指標GSI分級圖獲得以上信息,分級圖如圖1所示。

圖1 地質強度指標GSI 分級圖
廣義H-B 強度準則可以反映巖石和巖體固有的非線性破壞特點,以及結構面、應力狀態對強度的影響,能夠解釋低應力區、拉應力區和最小主應力對強度的影響,并適用于各項巖體的描述[10]。本文以福建地區某海上風電場項目的單樁基礎方案為例,使用Z-SOIL 有限元軟件,并采用H-B 巖體本構模型,對大直徑嵌巖單樁基礎受不同關鍵參數影響時的情況進行了系統地有限元模擬分析。
2 大直徑嵌巖單樁基礎參數的敏感性分析
2.1 基于GSI的巖體參數敏感性分析
福建地區某海上風電項目采用大直徑嵌巖單樁基礎方案,具體如圖2所示。
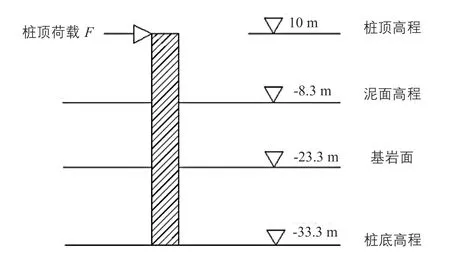
圖2 單樁基礎布置
該單樁基礎的直徑為6.5 m;樁頂標高為10 m;泥面處標高為-8.3 m;樁底標高按入巖深度10 m 考慮,取-33.3 m。單樁基礎土層參數如表2所示。
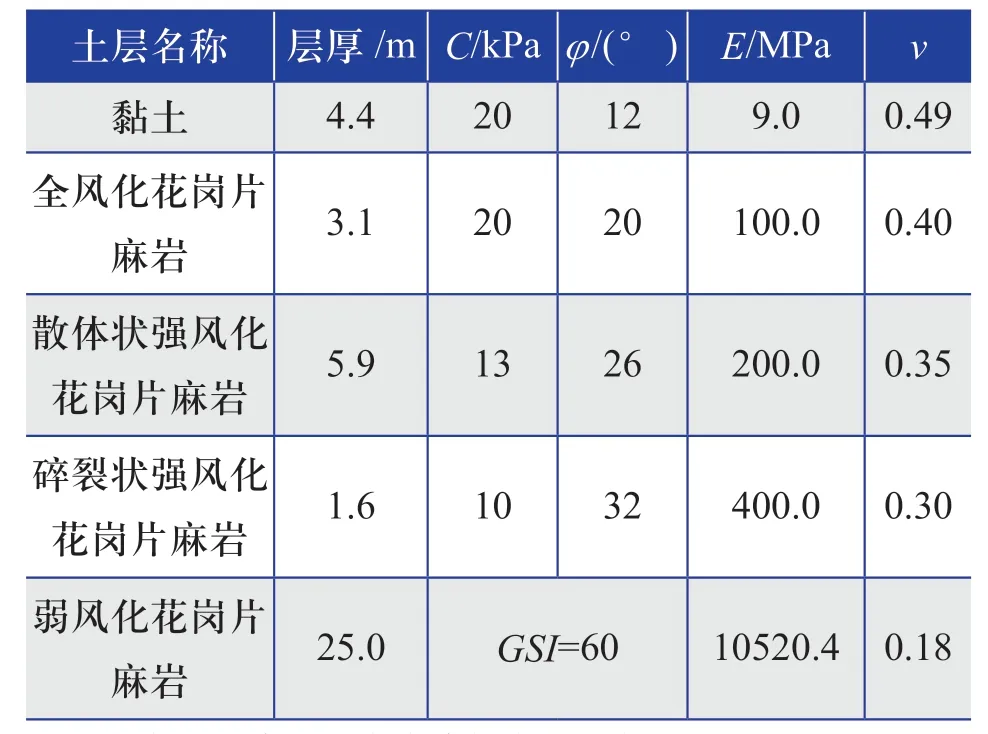
表2 單樁基礎土層參數
采用Z-SOIL 有限元軟件對單樁基礎進行三維有限元建模。鋼管樁樁身采用SHELL 單元,最下層弱風化花崗片麻巖采用H-B 巖體本構模型;其余土層采用摩爾-庫倫(M-C)土體本構模型,樁土間接觸面采用小變形接觸模型;樁頂荷載水平力F=1833 kN,豎向力G=5000 kN,扭矩N=1773 kN·m,彎矩M=121565 kN·m。單樁基礎有限元模型如圖3所示。
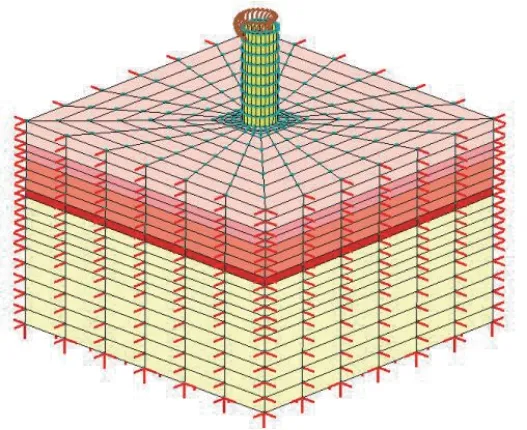
圖3 單樁基礎有限元模型
本文所使用的Z-SOIL 有限元軟件自帶H-B巖體本構模型及硬化土(HS)等多種土體本構模型,且巖體參數以GSI為標準輸入。弱風化花崗片麻巖巖體參數mi值按表1取值為30;根據圖1中的GSI分級規則,確定巖層GSI取60,巖體參數mb、s和a值可根據式(5)計算求得,擾動影響因素的取值為0.1。在確定巖體GSI值時,由于GSI的精確插值很難把控,因此需要研究巖體的GSI值和彈模E的變化對嵌巖單樁基礎抗變形能力的影響程度。通過改變底層弱風化花崗片麻巖的GSI的取值范圍,從10向100 變化,計算嵌巖單樁基礎的樁頂及泥面處的轉角和位移分別與彈模E和GSI的關系,計算結果如圖4~圖7所示。
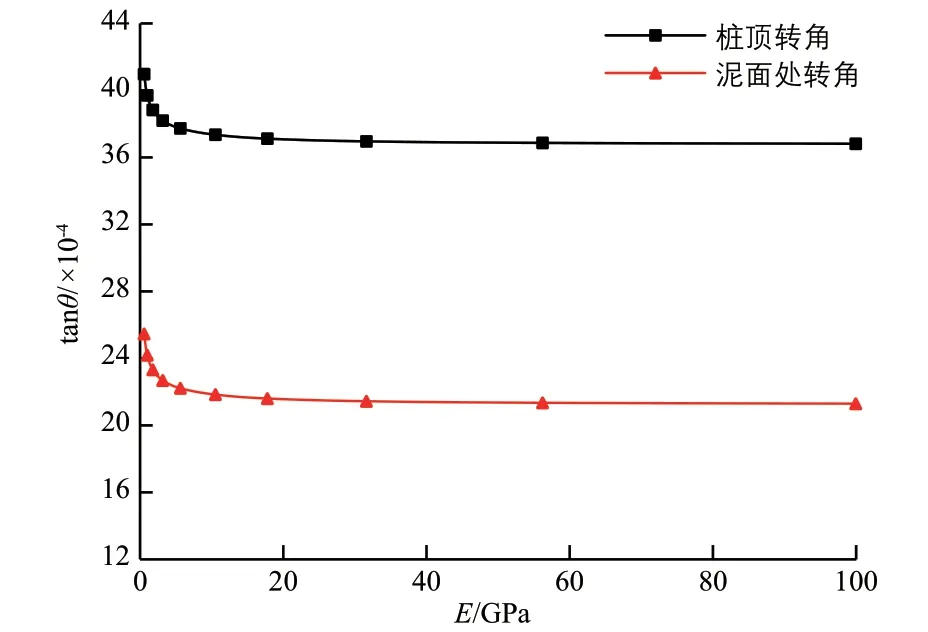
圖4 樁頂轉角、泥面處轉角與彈模E 的關系
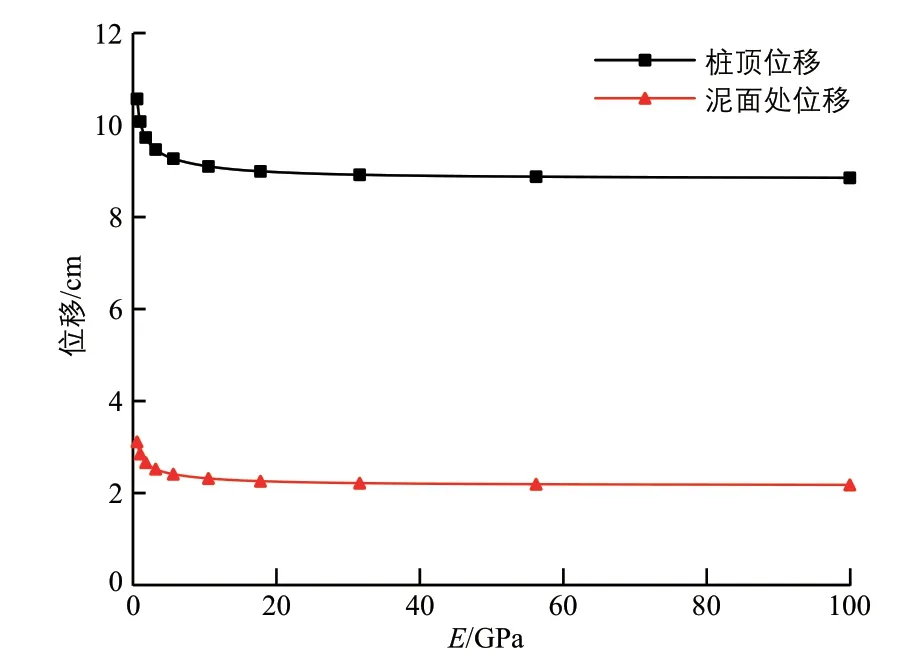
圖5 樁頂位移、泥面處位移與彈模E 的關系
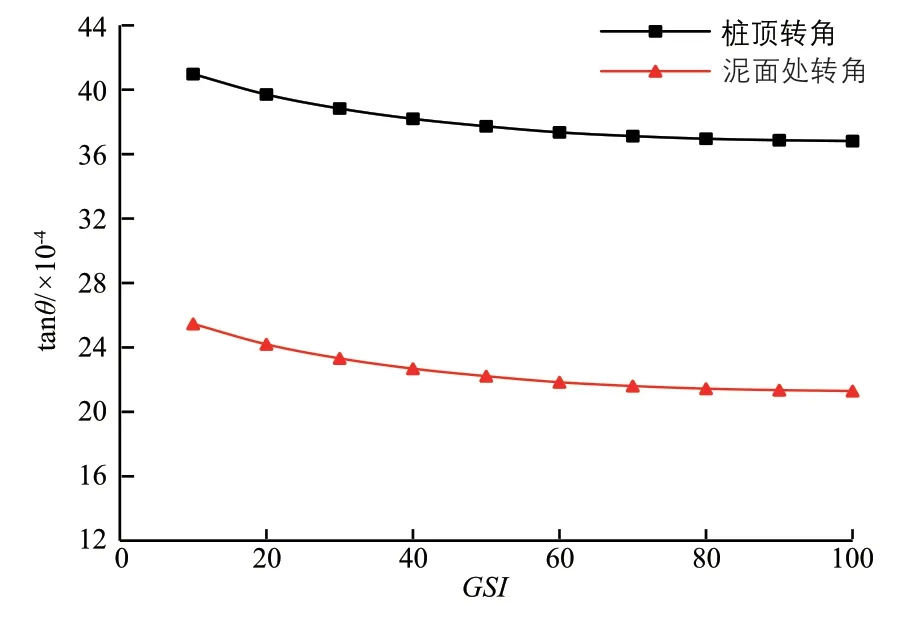
圖6 樁頂轉角、泥面處轉角與GSI 的關系
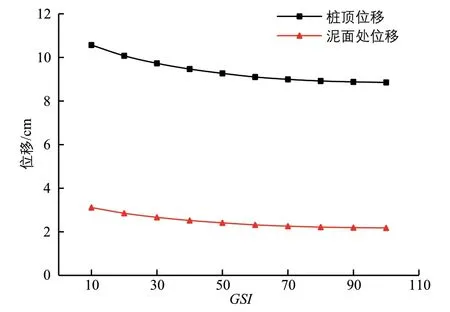
圖7 樁頂位移、泥面處位移與GSI 的關系
由圖4~圖7可知,隨著GSI值或彈模E的增大,樁頂轉角與位移及泥面處轉角與位移逐漸減小,即鋼管樁樁身變形逐漸減小,且減小趨勢變緩;彈模E為3.16 GPa 時為明顯拐點,即當持力層巖石GSI>40 時,彈模E或GSI值的變化對鋼管樁樁身變形已無顯著影響。
2.2 鋼管樁的樁身壁厚敏感性分析
鋼管樁的樁身壁厚對其抗變形能力影響很大,本節仍以上文所述模型為例進行分析。采用控制變量法,選取GSI為60 的巖層模型,樁身壁厚從30 mm 增至70 mm。由于本次計算是針對卸載后鋼管樁的殘余變形,因此土體采用HS 土體本構模型。該模型能更好地模擬土體的塑性特征,并可以很好地模擬卸載后鋼管樁的殘余變形。樁身壁厚與泥面處位移和轉角的有限元計算結果如圖8、圖9所示。
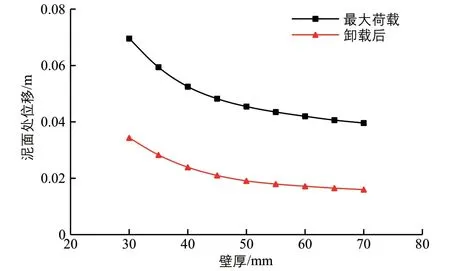
圖8 樁身壁厚與泥面處位移關系圖
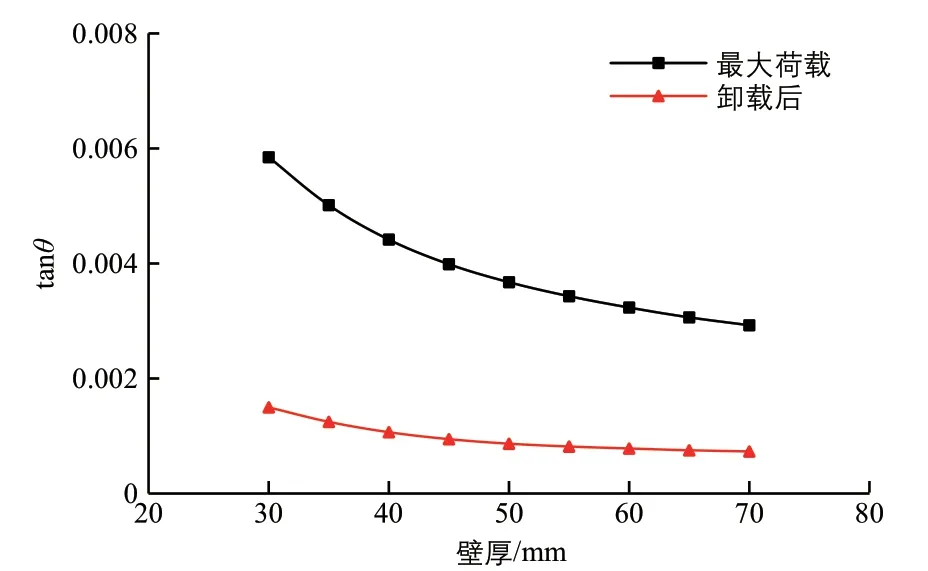
圖9 樁身壁厚與泥面處轉角關系圖
由圖8、圖9可知,鋼管樁樁身壁厚對單樁基礎抗彎性能有顯著影響。隨著樁身壁厚的增大,卸載后單樁基礎的泥面處位移及泥面處轉角均變小,且變化趨勢逐漸減緩。但由于樁身壁厚增加到一定程度時會產生邊際效應,因此,應選取合理的樁身壁厚。從圖中還可以看出,卸載后鋼管樁的殘余變形位移約為最大荷載下變形位移的1/2,轉角則平均約為最大荷載下的1/4。
2.3 入巖深度敏感性分析
在實際工程項目中,嵌巖單樁基礎的嵌巖施工對設備、人力、可施工時間的要求很高,而且由于場地地基經常會出現巖層起伏大、覆蓋層深淺不均的問題,對于基巖面位置的準確判斷還有一定難度,從而造成嵌巖施工整體難度大。因此,有必要研究嵌巖單樁基礎的入巖深度對其變形的影響,在把控嵌巖深度的同時還能提高經濟性,對實際工程有著重要的意義。
本節使用控制變量法,在保證其余條件不變的情況下,研究嵌巖深度3~8 m 的變化對嵌巖單樁基礎的變形影響,計算結果如圖10所示。
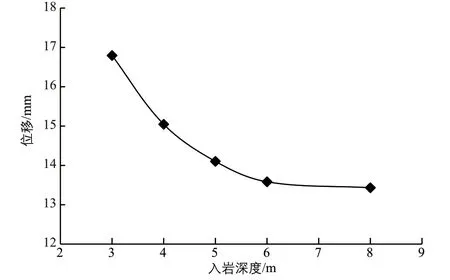
圖10 入巖深度與位移關系圖
由圖10可知,隨著嵌巖單樁基礎入巖深度的增加,單樁基礎的泥面處位移也急劇減小,在入巖深度達到6 m 時出現明顯的拐點,超過6 m 再增加入巖深度對單樁基礎的抗彎性能提升不顯著。
3 結論
本文通過對海上風電機組大直徑嵌巖單樁基礎結構設計時的參數進行分析,得到如下結論:
1)當持力層巖石物理性狀較好時,即當巖層GSI>40 時,此時GSI值的變化對嵌巖單樁基礎的變形計算結果影響不大。
2)鋼管樁的樁身壁厚增加到一定程度時,會產生顯著的邊際效應,因此在實際工程項目中,嵌巖單樁基礎的鋼管樁樁身壁厚可依據多組數值分析的結果選取,在符合規范要求的前提下,選取一個比較合理的值既能滿足其結構設計的要求,又能節省材料,降低基礎結構的工程造價。
3)嵌巖單樁基礎卸載后的最小殘余變形位移與其最大荷載下的變形位移呈一定的倍數關系,在實際工程的初步設計階段,可結合數值分析的結果,利用此規則來初步確定單樁基礎的殘余變形,從而進行下一步的設計工作。
4)當嵌巖單樁基礎的入巖深度達到一定程度時,其深度的增加對單樁基礎抗變形能力已無顯著提升。在實際工程中,可利用多種方法并結合數值分析的手段,確定嵌巖單樁基礎的合理嵌巖深度,從而減少不必要的消耗,以提升工程整體經濟性。

