應用半單連分數求解Pell方程

高 升

(合肥工業大學 數學學院，安徽 合肥 230601)

引 言

為方便討論,先引入一些記號和定義。本文提到的整數,均為有理整數。表示全體整數之集，+表示全體正整數之集，≥0表示全體非負整數之集，表示全體有理數之集。兩個整數a和b的最大公因子記作g.c.d.(a,b)。對任一實數x，“[x]”表示不超過x的最大整數。

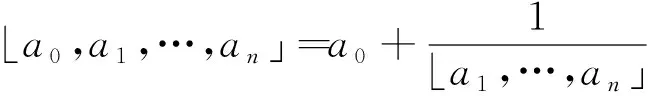
特別地，當a0∈，a1,a2,a3,…∈+時，稱「a0,a1,a2,…,an」為有限簡單連分數，稱「a0,a1,a2,……」為無限簡單連分數；當a0∈而a1,a2,a3,…為大于1的整數時，稱「a0,a1,a2,…,an」為有限半單連分數，稱「a0,a1,a2,……」為無限半單連分數。

(1)若存在m∈≥0和k∈+，使得?n≥m，都有an+k=an，則稱為循環數列，稱無限連分數「a0,a1,a2,……」或「a0,a1,a2,……」為循環連分數，稱k為該數列或該連分數的周期，此時將該連分數記為或

(2)若存在k∈+，使得?n≥0，都有an+k=an，則稱為純循環數列，稱無限連分數「a0,a1,a2,……」或「a0,a1,a2,……」為純循環連分數。

設Δ∈+非完全平方數，則可以用的無限簡單連分數展開式的漸近分數給出Pell方程x2-Δy2=±1的基本解(即最小正解)和全部正整數解。這是數論中廣為人知的經典結果(參見專著[2]的第3章第3節，[4]的第7章第6節，或者[5]中的定理3.18)。

對于在實二次域理論中應用廣泛的Pell方程x2-Δy2=4，求解過程更復雜。根據[3]中第1章引理2.4，如果非完全平方的正整數Δ=b2+4ac，其中a,b,c∈，|b|ac，g.c.d.(a,b,c)=1，那么可以用的無限簡單連分數展開式的漸近分數給出方程x2-Δy2=4的最小正解和全部正整數解。困難的地方在于，此時必須討論的無限簡單連分數展開式的最小周期的奇偶性。在最小周期為奇數和最小周期為偶數這兩種情況下，方程x2-Δy2=4的解的情況存在較大差異。

本文將以二次無理數的無限半單連分數展開式為工具給出Pell方程x2-Δy2=4的最小正解和全部正整數解。這種方法的優點是無需討論最小周期的奇偶性，在各種情況下都有統一的表達式。

1 預備知識

為了便于應用，將半單連分數的基本性質列舉如下(這些性質都是已知的，可以在[1]，[5],[6]中找到)。

引理2.1 設x1,…,xn為實數。若xj≥2(1j1，則「x1,…,xn」>1。

s-2=0，s-1=1，t-2=-1，t-1=0；sn=xnsn-1-sn-2，tn=xntn-1-tn-2，?n≥0；

又設a∈，則以下結論成立(假定其中出現的各連分數和分數都有意義)：

(1)?n∈+,?r∈≥0,有「x0,…,xn-1,xn,…,xn+r,a」=「x0,…,xn-1,「xn,…,xn+r,a」」；

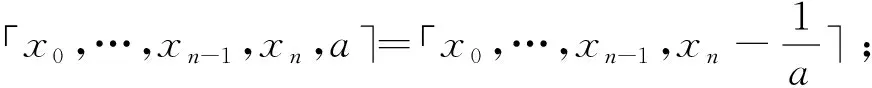
(2)?n∈≥0，有(約定：當n=0時，等式左邊就表示a)；

(3)?n∈≥0，有

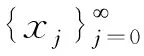
引理2.3(半單連分數的基本運算性質)(假定其中出現的各連分數和分數都有意義)

(1)?n∈+，有

(2)設a,b∈，n∈≥0，則且

(3)設k∈+，a2,a4,…,a2k-2∈，a1,a3,…,a2k-1∈+，則有

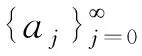
(1)?n∈≥0，?δ∈[1,+)，?ε∈(0,+)，都有「x0,…,xn,δ」<「x0,…,xn,δ+ε」；

(2)?n∈≥0，都有「x0,…,xn」>「x0,…,xn,xn+1」>x0-1；

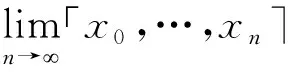
引理2.5(半單連分數展開式的存在性和唯一性)

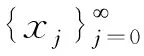
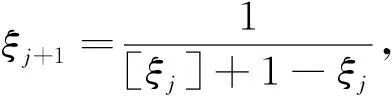
(i)?j≥1，有aj≥2；

(ii)?j≥0，有ξj=「aj,aj+1,aj+2,aj+3,…」；

(iii)ξ=「a0,a1,a2,a3,…」(即任一實數都可展開為無限半單連分數)；

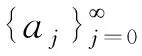
(i)?n≥0，有an=[θn]+1，且θ=「a0,…,an-1,θn」；

(ii)?n≥1，有θn≥1；

(iii)θ為有理數的充要條件是：存在j0≥0，使得aj=2(?j≥j0)；

(iv)θ為無理數的充要條件是：集合{j∈|j≥0,aj≥3}含無限多個元素。

引理2.6 設ξ為無理數且ξ=「a0,a1,a2,a3,…」，其中aj∈(?j≥0)，且aj≥2(?j≥1)，則ξ為二次無理數的充要條件是：存在m∈≥0和k∈+，使得?n≥m，有an+k=an。

引理2.7 設ξ為實二次無理數，則ξ可表示為無限純循環半單連分數的充要條件是：ξ>1且ξ的共軛數屬于開區間(0,1)。

以下命題是初等的，但對于本文主要定理的證明很有用。

證明 若已知g.c.d.(u1,v1)=1，則存在λ,μ∈，使得λu1+μv1=1，即于是，由已知條件可知即(r11λ+r12μ)u+(r21λ+r22μ)v=1，從而必有g.c.d.(u,v)=1。

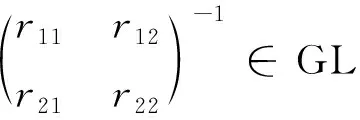
3 本文主要結果及其證明

引理3.1 若a,b,c∈，|b|ac，且Δ=b2+4ac非完全平方數(此時當然有a≠0且c≠0)，則必存在a0,a1,…,ak∈，其中a1,…,ak≥2，使得

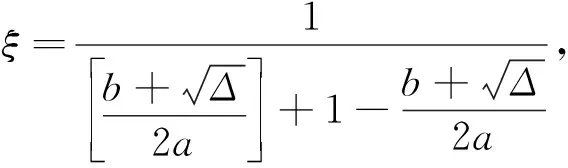
由引理2.3(4)可以推出以下結論。

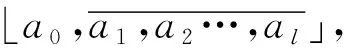
(1)若l=2k(其中k∈+)，則α可表示為無限循環半單連分數

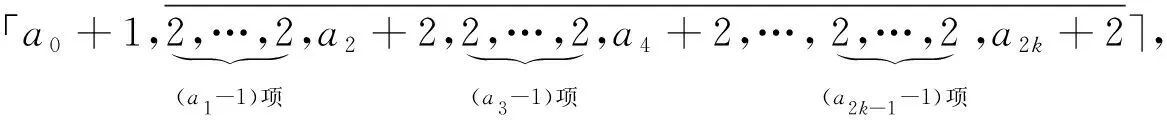
(2)若l=2k-1(其中k∈+)，則α可表示為無限循環半單連分數

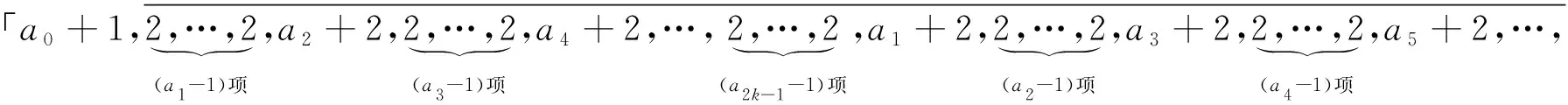
以下定理將該恒等式推廣到無限循環半單連分數的情形，系本文的原創。

(sk-1+βtk-1)m=smk-1+βtmk-1。

(1)

證明 由已知條件可知，存在整系數二次多項式ax2-bx-c(其中a,b,c∈，a>0)，使得ax2-bx-c=a(x-α)(x+β)。此時,有

由已知條件，可知s0=a0，t0=1。再由半單連分數的漸近分數的性質(引理2.2)可知，?n≥1，都有sn=ansn-1-sn-2，tn=antn-1-tn-2。

?m≥0，有α=「a0,…,amk,amk+1,amk+2,amk+3,amk+4,……」

=「a0,…,amk,a1,a2,a3,a4,……」

=「a0,…,amk,「a1,a2,a3,a4,……」」

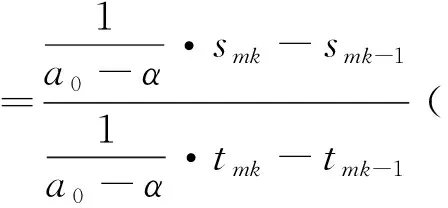
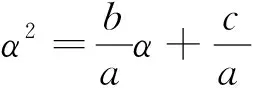
(2)

下面運用對m的歸納法來證明(1)式，即(sk-1+βtk-1)m=smk-1+βtmk-1(?m≥0)。

當m=0時結論顯然成立。

假設(1)式對非負整數m成立，我們分兩種情況來證明它對m+1仍然成立。

第一種情況，設k=1。此時sk-1=s0=a0，tk-1=t0=1。由歸納假設，有

(s0+βt0)m=(a0+β)m=sm-1+βtm-1，從而

(s0+βt0)m+1=(a0+β)m+1=(a0+β)m(a0+β)

=(sm-1+βtm-1)(a0+β)

=a0sm-1+β(a0tm-1+sm-1)+tm-1β2

=sm+βtm(由(2)式)，

所以此時(1)式對m+1仍然成立。

第二種情況，設k≥2。此時我們有

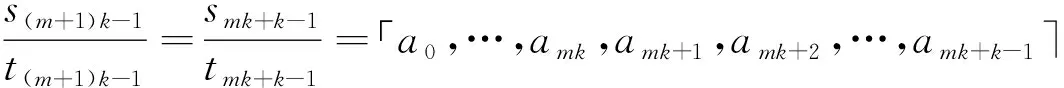
=「a0,…,amk,「a1,a2,…,ak-1」」

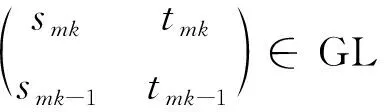
所以，由既約分數的性質可知

smktk-1+smk-1(sk-1-a0tk-1)=s(m+1)k-1，tmktk-1+tmk-1(sk-1-a0tk-1)=t(m+1)k-1。

(3)

于是，我們有

(sk-1+βtk-1)m+1=(sk-1+βtk-1)m(sk-1+βtk-1)

=(smk-1+βtmk-1)(sk-1+βtk-1)(由歸納假設)

=smk-1sk-1+β(smk-1tk-1+tmk-1sk-1)+β2tmk-1tk-1

=smk-1sk-1+(smk-a0smk-1)tk-1+β[(tmk-a0tmk-1)tk-1+tmk-1sk-1](由(2)式)

=s(m+1)k-1+βt(m+1)k-1(由(3)式)，

即(1)式對m+1仍然成立。

推論3.4 設實二次無理數α=「a0,a1,a2,a3,……」=「b0,b1,b2,b3,……」，其中a0,b0∈，和都是正整數列，且bj≥2(?j≥1)；又設?n≥1，有an+l=an和bn+m=bn，且l和m分別為循環簡單連分數「a0,a1,a2,a3,……」和循環半單連分數「b0,b1,b2,b3,……」的最小周期。設β為α的共軛數的相反數，又設其中p,s∈，q,t∈+，g.c.d.(p,q)=g.c.d.(s,t)=1，則以下結論成立：

(1)當l為偶數時，必有s+βt=p+βq；

(2)當l為奇數時，必有s+βt=(p+βq)2。

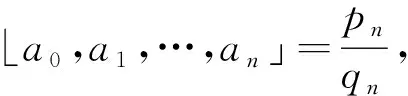
(1)設l=2k(k∈+)。由引理3.2(1)可知，

=「a0,a1,a2,a3,…,a2k-1」(由引理2.3(3))

由既約分數的性質可知s=p，t=q，從而s+βt=p+βq。

(2)設l=2k-1(k∈+)。由引理3.2(2)可知，

=「a0,a1,a2,a3,…,a2k-1,a1,a2,a3,a4,…,a2k-2」(由引理2.3(3))

=「a0,a1,a2,a3,…,a2k-1,a2k,a2k+1,a2k+2,a2k+3,…,a4k-3」

所以s=p2l-1且t=q2l-1，進而s+βt=p2l-1+βq2l-1=(pl-1+βql-1)2=(p+βq)2。

以下定理是本文的主要結果，用無限循環半單連分數的漸近分數給出了一類在代數數論中有重要應用的Pell方程的最小正解和全部正整數解。

定理3.5 設a,b,c∈，|b|ac，g.c.d.(a,b,c)=1，且Δ=b2+4ac非完全平方數。記設α的無限半單連分數展開式為「a0,a1,a2,a3,…」，它的最小周期為k，其中為整數列，當j≥1時恒有aj≥2。對每個n≥0，設「a0,a1,…,an」=sn/tn，其中sn∈，tn∈+，g.c.d.(sn,tn)=1，則以下結論成立：

(1)Pell方程x2-Δy2=4的最小正解為sk-1+βtk-1；

(2){(x,y)∈+×+|x2-Δy2=4}

證明 設α的無限簡單連分數展開式為「A0,A1,A2,A3,……」，最小周期為h，其中A0∈，Aj∈+(?j≥1)。由[3]中第1章引理1.2可知，必有對每個m≥0，令「A0,A1,…,Am」=pm/qm，其中pm∈，qm∈+，g.c.d.(pm,qm)=1。

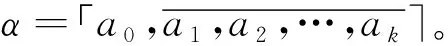
(2)這可以從[3]中第1章引理2.2和本文的定理3.3直接推出。

致謝

作者感謝趙立璐教授對本文引理3.2提供的幫助。