捷聯式航空重力測量系統的數據處理方法比較與分析

修 睿，郭 剛，薛正兵，李東明，李海兵

（1.青島海洋科學與技術試點國家實驗室,青島266237；2.北京航天控制儀器研究所,北京100039）

0 引言

航空重力測量是利用機載重力測量系統進行的空中重力測量，是重力測量的重要手段。目前，國際上的航空重力測量系統主要為平臺式系統。近年來，國內自主研制出了基于捷聯慣性技術的新型重力測量系統，其被稱之為捷聯式重力測量系統。捷聯式航空重力測量系統采用了捷聯慣性/GPS組合導航算法技術，可計算出重力傳感器敏感軸與當地地理水平面的不垂直度并予以數學校正，即可建立與物理平臺等價的數學平臺，具有體積小、質量小、可靠性高的優點。

在飛行作業過程中，由飛機機體高速運動帶來的高頻振動不可避免地對重力傳感器產生了高頻干擾。為盡可能消除或減弱這些高頻噪聲的影響，需采用重力數據濾波方法對重力傳感器輸出進行處理，從而獲得高精度的重力異常值。

目前，比較常用的濾波方法主要包括有限脈沖響應FIR低通濾波、無限脈沖響應IIR低通濾波、Kalman濾波、RC濾波、Gauss濾波等。本文采用FIR低通濾波、零相移濾波、標準Kalman濾波和正反Kalman濾波4種方法，結合實際飛行試驗數據，對4種濾波方法的處理結果進行了比對。同時，捷聯式重力測量系統的數學平臺精度也直接影響著重力傳感器敏感軸指向的校正精度，從而影響著最終的重力測量精度。本文對基于GPS輔助的SINS/GPS與基于DGPS輔助的SINS/DGPS 2種數學平臺計算方法獲得的重力測量數據結果進行了比對。

1 系統組成及數據處理過程

1.1 捷聯式重力測量系統的測量原理

捷聯式海空重力儀（SAG）將重力傳感器固聯集成于SINS/GPS組合導航系統，重力傳感器為高精度石英撓性加速度計。捷聯式海空重力儀與顯控記錄裝置、UPS一起構成了捷聯式海空重力測量系統。

重力傳感器敏感軸、捷聯慣性系統天向軸、載體天向軸三者平行，重力傳感器敏感軸的輸入信息包含了重力信息沿載體天向軸方向的分量及沿載體天向軸方向的運動加速度。通過SINS/GPS組合導航計算出載體姿態，即建立數學平臺，將重力傳感器輸出進行指向校正，可獲得垂直于當地地理水平面的重力與垂向運動加速度之和；再利用GPS系統測量信息估算出垂向運動加速度，即可獲得重力信息；再經濾波處理濾除振動等產生的干擾噪聲，以及厄缶改正、高度改正、正常重力改正等，最終可獲得自由空間重力異常值。

1.2 數據處理過程

捷聯式重力測量數據處理流程包括導航解算部分和重力異常提取部分，重力異常提取過程在導航解算的基礎上進行。導航原始數據（陀螺、加速度計的原始脈沖）經誤差補償和純慣性導航解算后，與GPS數據進行組合導航和濾波處理，獲得純慣性導航的姿態誤差、速度誤差、位置誤差，修正得到東北天向的比力值和修正后的載體速度、位置信息。將載體位置信息進行2次差分處理后，可得到載體的運動加速度。結合差分GPS速度、位置信息和3個比力信息，可以得到重力異常粗值。經過濾波處理和各項改正后，可得到精確的自由空間重力異常值，其計算公式為[1]

式中，δg為自由空間重力異常值，gb為基準點參考重力值，為比力和比力初值，為運動加速度改正，δaF為空間改正，δaE為厄缶改正，γ0為正常橢球面上的重力值。

自由空間重力異常提取由事后處理軟件完成，其流程如圖1所示。

圖1 自由空間重力異常提取處理流程圖Fig.1 Flowchart of free-space gravity anomaly extraction and processing

2 重力數據處理方法介紹

2.1 FIR低通濾波

目前，FIR濾波器主要涉及窗函數設計法、頻率抽樣設計法和Chebyshev逼近法，這里主要對常用的窗函數設計法進行介紹。

有限脈沖響應FIR數字濾波器要求用有限長的單位沖擊響應h（n）來逼近無限長的理想濾波器的單位沖擊響應hd（n），最常用和有效的方法就是用1個長度為N的窗函數序列ω（n）來截取hd（n）的主要成分

實際上，窗函數設計FIR濾波器的核心是由給定的頻率特性通過加窗確定有限長單位脈沖響應序列h（n）。 工程中常見的窗函數包括以下幾種：矩形窗、三角窗、Hanning窗、Hamming窗、Blackman窗、Kaiser窗，其性能如表1所示[2-4]。

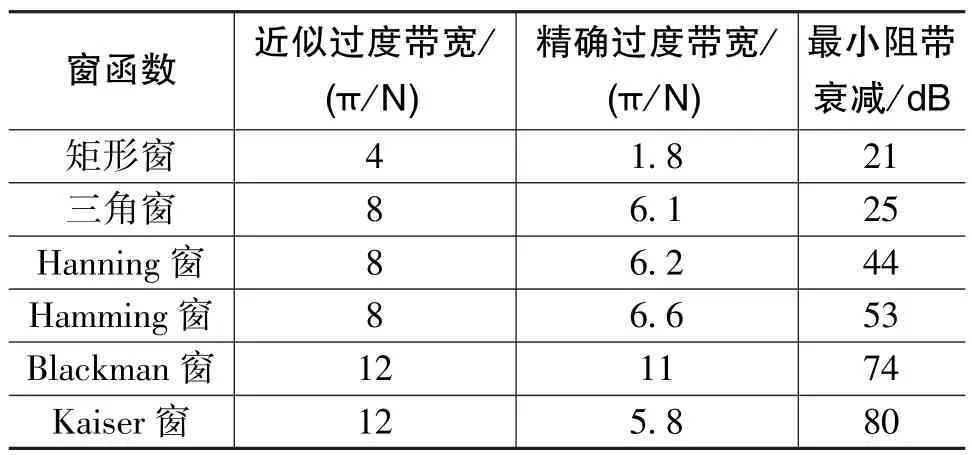
表1 常用窗函數的性能比較Table 1 Performance comparison of commonly used window functions

本文中用到的FIR濾波器采用Hanning窗，采樣頻率fs=1Hz，歸一化截止頻率fc=0.005Hz，階數N=600。

2.2 零相移濾波

零相移濾波是指信號序列在經過濾波器濾波之后，信號序列相位不發生變化，系統函數的相位響應為0，濾波后效果更平滑且信號無位移。零相移濾波算法流程如圖2所示，需進行正向、反向2次濾波。

假設輸入信號序列為 [x（n）]，n=1，2，…，n0，[y（n）]為信號[x（n）]時域翻轉后的序列，將 2個信號分別進行沿x軸、y軸的延拓后，進行雙邊Z變換，得到

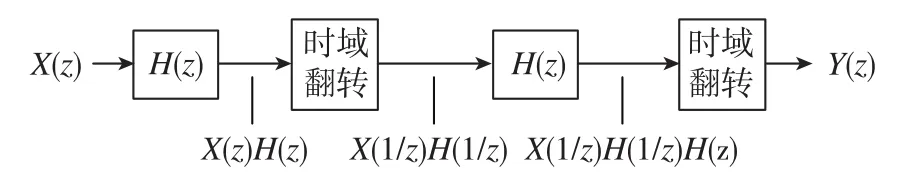
圖2 零相移算法原理圖Fig.2 Schematic diagram of zero phase shift algorithm

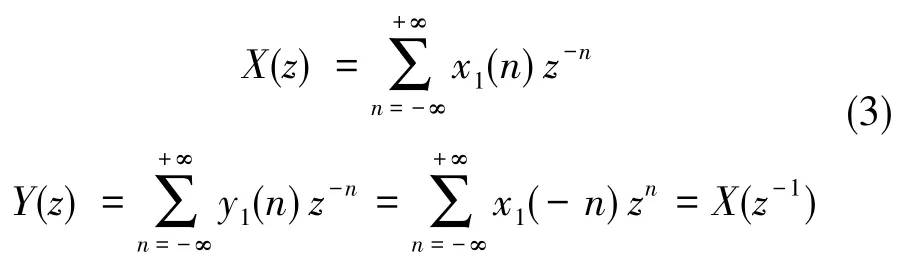
由算法流程，設傳遞函數為H（z），則濾波器輸出信號序列為

經過二次濾波和翻轉輸出的信號序列為

本文中零相移濾波器的采樣頻率fs=1Hz，歸一化截止頻率fc=0.005Hz，階數N=600。

2.3 標準Kalman濾波

設tk時刻的被估計狀態Xk受系統噪聲序列Wk-1驅動，其驅動機理由下述狀態方程描述[5-7]

對Xk的量測滿足線性關系，量測方程為

式中，Φk，k-1為tk-1時刻至tk時刻的一步轉移陣，Γk-1為系統噪聲驅動陣，Hk為量測陣，Vk為量測噪聲序列，Wk-1為系統激勵噪聲序列。

Kalman濾波方程為：

（1）狀態一步預測

（2）狀態估計

（3）濾波增益

（4）一步預測均方誤差

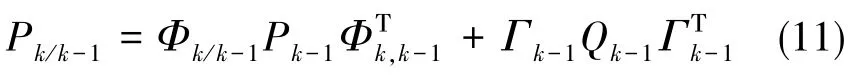
（5）估計均方誤差

式中，Pk為估計誤差方差陣，Kk為加權矩陣，Pk/k-1為一步預測均方誤差，Xk/k-1為狀態一步預測，Rk為量測噪聲方差陣。

2.4 正反Kalman濾波

正反Kalman濾波是連續進行2次方向相反的Kalman濾波，并將正向、反向2次濾波結果進行加權求和，能夠充分利用正向Kalman濾波的狀態估計量、一步狀態估計、誤差協方差矩陣等參數信息。該方法克服了標準離散Kalman濾波的精度缺陷問題，優化了濾波處理結果[8-10]。

正反Kalman濾波的正向過程即為標準離散型Kalman濾波。

反向過程的濾波方程為

預測過程方程為

加權過程方程為

正反Kalman狀態量是正向狀態估計量xk與反向狀態估計量xf（k/k-1）的加權求和，權重為Xzf（k）和Pzf（k）。

3 飛行試驗結果比對

3.1 飛行試驗概況

采用上述FIR低通濾波、零相移濾波、標準Kalman濾波、正反Kalman濾波4種濾波方法，對SAG某架次的飛行試驗數據進行了處理，并將處理結果進行了精度比對。

在本次試驗過程中，飛機平穩飛行，飛行平均高度為800m，飛行平均速度為60m/s，飛行軌跡為8條東西重復測線、2條南北測線。測線結果如圖3所示，圖中的經緯度進行了人為偏移。

圖3 東西重復測線和南北測線結果Fig.3 Results of East-West repeat survey lines and North-South survey lines

3.2 基于SINS/GPS、SINS/DGPS組合導航的結果比對

分別采用GPS輔助導航和DGPS輔助導航進行導航解算，2種組合導航解算得到的比力值、航姿、速度、位置在測線段的曲線分別如圖4～圖7所示，圖中的經緯度進行了人為偏移。其中，紅色曲線為GPS輔助導航的解算結果，藍色曲線為DGPS輔助導航的解算結果。對2種組合導航東西重復線上的比力、速度、航姿信息進行均值和標準值的比對，其結果如表2所示。

圖4 2種組合導航解算測線段比力值的結果比對Fig.4 Comparison of specific force value between two kinds of integrated navigation solution survey lines

圖5 2種組合導航解算測線段航姿的結果比對Fig.5 Comparison of attitude angle between two kinds of integrated navigation solution survey lines

圖6 2種組合導航解算測線段速度的結果比對Fig.6 Comparison of velocity between two kinds of integrated navigation solution survey lines

圖7 2種組合導航解算測線段位置的結果比對Fig.7 Comparison of position between two kinds of integrated navigation solution survey lines

表2 2種組合導航測線段比力、姿態、速度的信息比對Table 2 Comparison of specific force，attitude angle and velocity between two kinds of integrated navigation solution survey lines

由圖4～圖7所示的2種組合導航的比力值、航姿、速度、位置結果的比對曲線可以看出，紅色曲線和藍色曲線均完全重合，即GPS輔助導航結果與DGPS輔助導航的結果基本完全一致。由表2的比對數據可以看出，各項信息的均值和標準值基本沒有差異，GPS輔助導航結果與DGPS輔助導航結果一致，采用單點GPS或差分GPS對于導航信息和比力值的坐標分解沒有影響。

3.3 基于SINS/GPS、SINS/DGPS組合導航的重力數據處理結果比對

分別對基于SINS/GPS和SINS/DGPS組合導航的重力測量數據，采用FIR低通濾波、零相移濾波、標準Kalman濾波、正反Kalman濾波方法對測區重力異常粗值進行濾波處理。其中，在重力數據處理階段的各項改正中代入的速度、位置、高度數據均為差分GPS數據。處理結果分別如圖8、圖9所示，藍色曲線為FIR低通濾波結果，紅色曲線為標準Kalman濾波結果，綠色曲線為正反Kalman濾波結果，黑色曲線為零相位濾波結果。

圖8 基于SINS/GPS的4種濾波方法處理重力異常結果比對Fig.8 Comparison of four filtering methods for gravity anomaly results based on SINS/GPS

圖9 基于SINS/DGPS的4種濾波方法處理重力異常結果比對Fig.9 Comparison of four filtering methods for gravity anomaly results based on SINS/DGPS

對8條東西重復測線上的重力異常值進行濾波處理，結果比對如圖10、圖11所示。藍色曲線為FIR低通濾波結果，紅色曲線為標準Kalman濾波結果，綠色曲線為正反Kalman濾波結果，黑色曲線為零相移濾波結果。

為了更好地比較4種濾波方法及不同組合導航條件下的重力異常數據處理結果，表3列出了這8條東西重復測線在水平調整后的內符合精度。其中，最后1列為所有測線的內符合總精度。

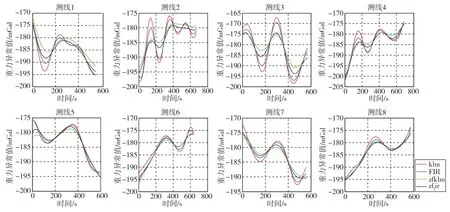
圖10 基于SINS/GPS的8條東西重復測線的4種濾波方法比對Fig.10 Comparison of four filtering methods on eight kinds of East-West repeated survey lines based on SINS/GPS

圖11 基于SINS/DGPS的8條東西重復測線的4種濾波方法比對Fig.11 Comparison of four filtering methods on eight kinds of East-West repeated survey lines based on SINS/DGPS

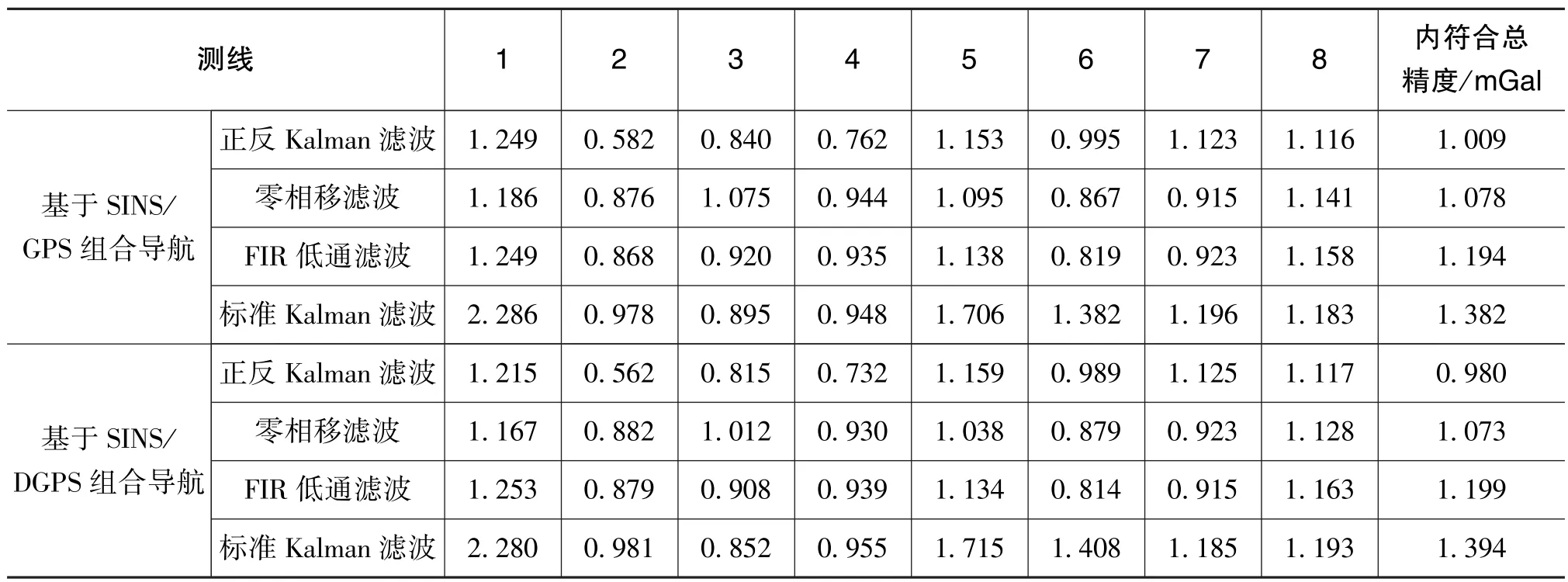
表3 重復測線內符合精度評估Table 3 Accuracy evaluation in repeated survey lines

在表3中，以每條重復測線的內符合精度及所有重復測線的總內符合精度進行評判，分別對采用單點GPS進行組合導航后的相關重力測量數據處理結果及采用差分GPS進行組合導航后的相關重力測量數據處理結果進行比對，并列出了采用4種濾波方法所得的重復測線內符合精度，均為水平調整后的結果。

每條測線的均方根誤差及標準差計算方法如下

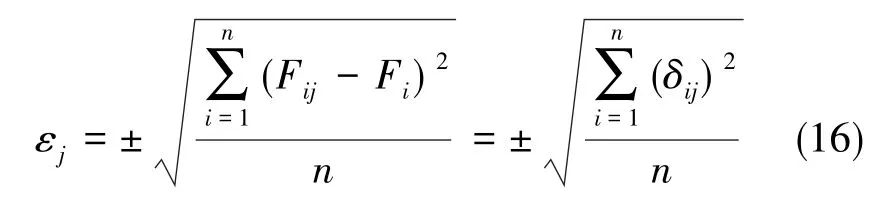
式中，δij為第j條重復公共段各點觀測值與該點各重復線觀測值的平均值之差，即

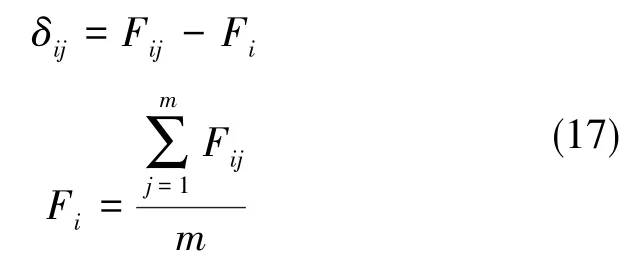
m為重復線數目，n為重復線公共段數據點數。

所有重復線測試數據的總內符合精度計算公式為

從表3基于SINS/GPS組合導航的重力數據處理結果的最后一列，即所有重復測線的內符合總精度可以看出：2種Kalman濾波方式相比，正反Kalman濾波的均方根誤差最小，為1mGal左右，標準Kalman濾波的均方根誤差最大，達到近1.38mGal，兩者相差0.38mGal；2種低通濾波相比較為接近，FIR低通濾波的均方根誤差為1.19mGal，零相移濾波的精度為1.08mGal，略優于FIR低通濾波；而零相移濾波與正反Kalman濾波的結果相近，后者精度略高。

從表3基于SINS/DGPS組合導航的重力數據處理結果的最后1列數據可以看出：正反Kalman濾波效果最好，精度達到了0.98mGal；零相移濾波其次，達到了1.07mGal；FIR低通濾波的精度相對較差，為1.2mGal；標準Kalman濾波的精度結果為1.39mGal。

將兩者比對可以看出：采用差分GPS數據進行組合導航處理之后得到的重力測量數據，相比于采用單點GPS數據進行組合導航得到的重力測量數據，精度基本接近，相差約為0.01mGal。

從以上分析可以看出：正反Kalman濾波方法的處理精度最高，優于2種低通濾波和單向標準Kalman濾波；正反Kalman濾波得到的重力異常曲線與另外3種曲線相比最為平滑，對高頻噪聲的去噪效果最好；零相移濾波與FIR低通濾波相比，其優點在于可進行正反2次低通濾波，對高頻噪聲的去噪效果更好，并抵消了正反相位移動的偏差，相對而言結果更為準確。同時，采用SINS/DGPS組合導航得到的重力測量數據，相比于采用SINS/GPS組合導航得到的重力測量數據，處理結果基本一致，這說明采用單點GPS或差分GPS進行組合導航，對導航解算結果和重力信息數據的處理結果并不影響。

4 結論

本文對FIR低通濾波、零相移濾波、標準Kalman濾波、正反Kalman濾波4種重力異常提取方法進行了比對，并采用以上方法分別對基于SINS/GPS和SINS/DGPS組合導航的實際SAG飛行試驗數據進行了處理。重復測線的內符合精度統計結果表明，正反Kalman濾波與零相移濾波的結果精度相對較高，分別達到了0.98mGal和1.07mGal，正反Kalman濾波略優于零相移濾波；標準Kalman濾波的精度相對較差，精度與正反Kalman濾波相差近0.4mGal；FIR低通濾波的精度適中，與零相移濾波相比略有差距。本文驗證了這4種濾波方法的實用性和優劣性，以及重力異常模型和窗函數設計的合理性。同時，也驗證了單點GPS輔助導航與DGPS輔助導航的結果相同，即采用何種組合導航方式不影響后續重力數據的處理精度。本次試驗也從側面反映了SAG重力儀的測量精度，其內符合精度可達0.98mGal。