三軸磁通門傳感器誤差校正方法
羅建剛,李海兵,2,劉靜曉,李海虎,張 峰
(1.青島海洋科學與技術試點國家實驗室,青島266237;2.北京航天控制儀器研究所,北京100039)
0 引言
三軸磁通門傳感器具有良好的魯棒性和較高的分辨率,在軍事和民用領域得到了廣泛應用[1-4],如地磁匹配導航、資源勘探、地球科學研究等。三軸磁通門傳感器的每個軸只敏感當前軸向的磁場值,使其具備矢量磁測功能。利用三軸磁通門傳感器搭配高精度姿態(tài)儀進行矢量磁測,便可以實時解算出地磁場的多個要素[3]。三軸磁通門傳感器具有傳統(tǒng)標量磁力測量不可比擬的優(yōu)勢,因此近年來矢量磁測已成為研究熱點。國家重點研發(fā)計劃 “深海關鍵技術與裝備”、山東省重大科技創(chuàng)新工程 “海洋高端裝備技術創(chuàng)新工程”等都對矢量磁力測量有所支持。
地磁場屬于微弱信號,在被測量時極易受到環(huán)境噪聲和儀器自身的干擾和誤差的影響。因此,矢量磁力測量中一項重要任務就是對儀器誤差進行補償校正。當外部環(huán)境磁場恒定時,理想三軸磁通門傳感器輸出的總場模值應是恒定、不隨姿態(tài)變化的;但實際上,由于三軸磁通門傳感器存在三軸非正交誤差[5]、零偏誤差和標度系數(shù)誤差,這使得三軸磁通門傳感器輸出的總場模量值是隨姿態(tài)而變化的,此項誤差被稱為轉向差[6-7]。
仿真計算表明,當三軸磁通門傳感器在地磁場環(huán)境(約50000nT)中自由轉動時,僅僅單個軸與標準正交軸之間存在的0.5°的角度偏差,就會為相應敏感軸帶來-436nT~+436nT的誤差,會為總場模量值帶來-226nT~+226nT的誤差。因此,三軸磁通門傳感器轉向差的存在嚴重影響了其測量精度。隨著三軸磁通門傳感器應用的愈加廣泛,對其轉向差的數(shù)學校正方法的研究也被重視起來。
文獻[7]~文獻[10]對三軸磁通門傳感器轉向差提出了不同的校正算法,并取得了一定的校正效果。但上述算法或計算復雜不易實現(xiàn),或只給出了校正模型而不能得出各項誤差參數(shù)值,或只能得出部分誤差參數(shù),或僅停留在仿真層面而未做實驗驗證。因此,上述算法均有不足之處,均需要改進。
本文通過分析轉向差的產(chǎn)生機理,建立了誤差模型。基于總場模值不隨姿態(tài)變化的思想,利用最小二乘法估算得出各項誤差參數(shù),并進行了仿真和實驗驗證。結果證明,該算法對誤差參數(shù)估算準確,所得誤差參數(shù)對不同磁場環(huán)境下實測數(shù)據(jù)的轉向差均具有較好的校正效果,且算法簡單高效,實用性強。
1 誤差分析與建模
為了校正三軸磁通門傳感器的轉向差,首先需要分析誤差產(chǎn)生的機理,然后建立誤差參數(shù)估算模型。
1.1 誤差參數(shù)分析
理想情況下,三軸磁通門傳感器的三個敏感軸之間是相互正交的。但實際上,由于加工和安裝工藝的限制,三個敏感軸之間不可能做到完全正交。因此,其測量得到的空間磁場三分量值與磁場正交三分量值存在偏差,此項誤差稱為非正交誤差。
設OXYZ為三軸正交坐標系,空間磁場向量在正交坐標系三個軸OX、OY、OZ上的投影值分別為Bx、By、Bz。三軸磁通門傳感器所測的是空間磁場向量在各軸方向上的投影值。設磁通門傳感器三個軸所構成的坐標系為O1X1Y1Z1,空間磁場向量在其三個軸O1X1、O1Y1、O1Z1上的投影值分別為Bx1、By1、Bz1。
為簡化模型,設三軸磁通門傳感器坐標系和三軸正交坐標系原點重合,OZ和OZ1共軸,OY1位于OYZ面內(nèi),如圖1所示。磁通門坐標系三軸間并非完全正交,設OY1與OY的夾角為γ,OX1與OXY面的夾角為β,OX1在OXY面上的投影與OX的夾角為α。
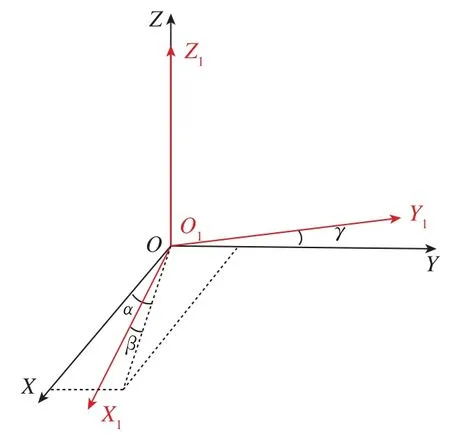
圖1 磁通門傳感器坐標系與正交坐標系的關系Fig.1 Relationship between fluxgate magnetometer coordinate system and orthogonal coordinate system

其中,A為變換矩陣
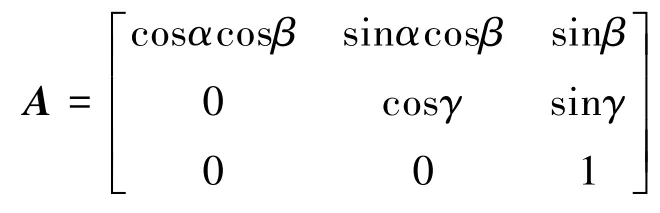
由于α、β、γ均為小角度,因此有cosα≈1、 cosβ≈1、 cosγ≈1、 sinβ≈β、 sinγ≈γ,則矩陣A可簡化為
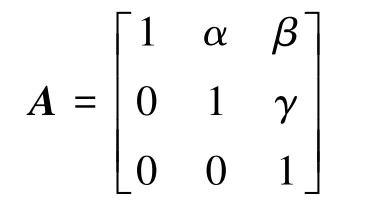
當在三軸磁通門傳感器三個敏感軸方向施加相同磁場時,其輸出值應該是一致的。但由于磁通門傳感器三軸間的靈敏度和放大調(diào)理電路可能存在差別,這導致三個軸在承受相同的磁場時,其輸出值可能不同,此項誤差被稱為標度系數(shù)誤差。一般情況下,含有標度系數(shù)誤差的磁傳感器輸出值與真實磁場值呈比例關系,設標度系數(shù)誤差矩陣為K,則有

三軸磁通門傳感器自身的一些鐵磁性物質由于長期處在磁場環(huán)境下,會被環(huán)境磁場磁化而產(chǎn)生剩磁。此外,傳感器及數(shù)據(jù)采集模塊電路也會產(chǎn)生零點漂移。由剩磁和電路零點漂移產(chǎn)生的誤差被稱為零偏誤差[11]。零偏誤差相當于在磁通門傳感器的各軸上疊加了一個固定磁場,使被測磁場的分量值發(fā)生了偏移。設零偏誤差為b,則有
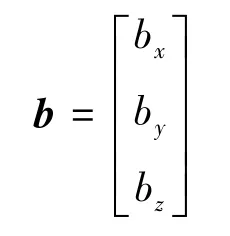
通過上述分析,可以通過改善加工與安裝工藝、選擇性能更優(yōu)良的材料、提升電路精度與穩(wěn)定性等手段降低三軸磁通門傳感器的轉向差。但當上述手段都達到極限時,只能通過對實測數(shù)據(jù)進行校正的方法來抑制轉向差。
1.2 建立誤差參數(shù)估算模型
通過上一節(jié)對誤差參數(shù)的分析,可得出磁通門傳感器測量值與被測磁場真實值之間的關系式
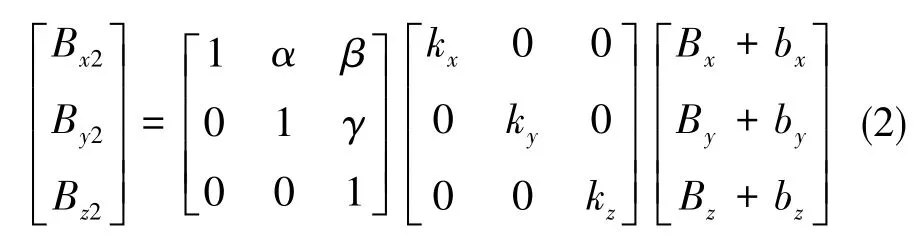
矩陣A和K均滿秩,為可逆矩陣,通過變換可得到由傳感器測量值求被測磁場真實值的公式
令
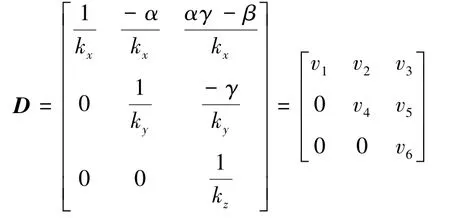
則式(3)可表示為

根據(jù)式(4),只要求出α、β、γ、kx、ky、kz、bx、by、bz這9個誤差參數(shù),就能夠通過三軸磁通門傳感器測量值計算得到被測磁場的真實值,消除轉向差。因此,轉向差校正問題就轉變?yōu)榍蠼馍鲜?個未知參數(shù)的問題。
對式(4)取平方,得到總場模值的平方
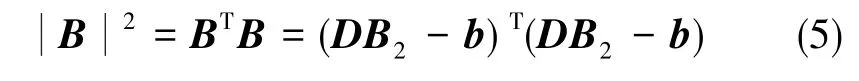
把式(5)展開并舍棄相對小量,得
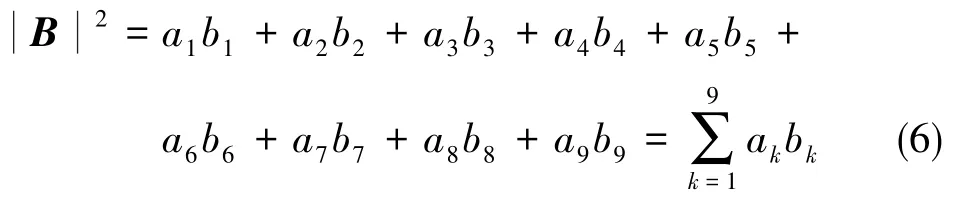
其中,
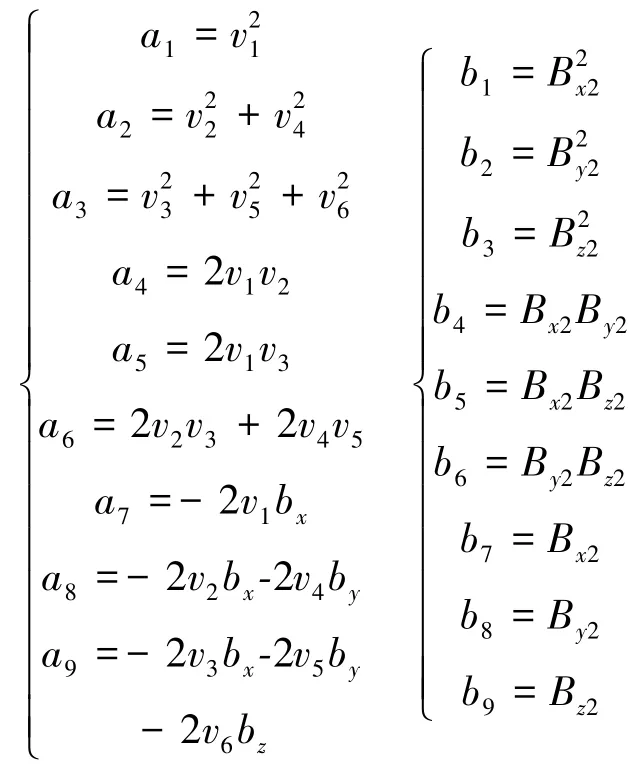
在穩(wěn)定磁場環(huán)境中自由轉動磁通門傳感器,記錄n(n>9)種姿態(tài)下磁場測量值B2(i)(i=1,2,…,n),對應可計算得到n個總場模值的平方。 另外,給出一個總場模值的期望值,其可通過高精度標量磁力儀測得,或通過對測量所得總場模值取平均得到[8,12]。根據(jù)最小二乘法的原理[13],要求解得到上述9個未知參數(shù)的最優(yōu)結果,只需使偏差的平方和(即2-范數(shù))取最小值。其中,。 令
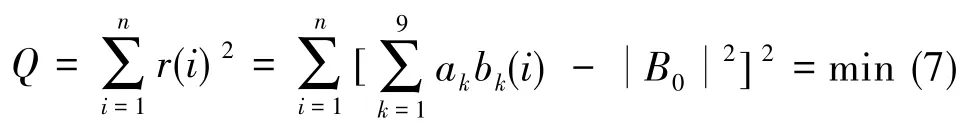
上述問題可歸結為求解多元函數(shù)的極值問題。由多元函數(shù)極值的必要條件,令
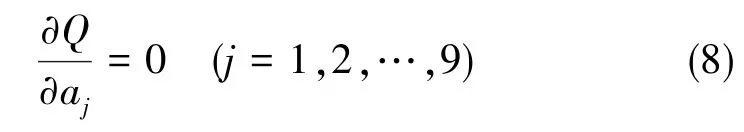
得
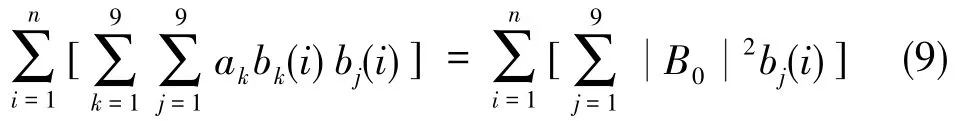
這是關于ak(k=1,2,…,9)的線性方程組,求解此方程組得到的ak(k=1,2,…,9)是滿足式(7)的最優(yōu)解。隨后,通過計算可以得出α、β、γ、kx、ky、kz、bx、by、bz的值,進而可以對磁場測量值進行校正,消除轉向差。
式(9)可表示為矩陣形式

由于磁場數(shù)據(jù)B2(i)(i=1,2,…,n)是在不同姿態(tài)下采集得到的,且n>9,因此式(10)的系數(shù)矩陣GGT非奇異,則可解得a,且其存在唯一解[13],有
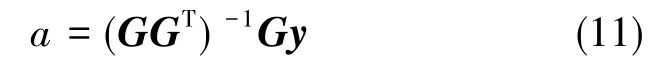
2 仿真驗證
通過Matlab進行仿真計算,驗證算法的有效性。模擬三軸磁通門傳感器在固定磁場空間中的自由轉動,采集得到100組三分量磁場數(shù)據(jù),空間總場模值設定為50000nT。在采集模擬數(shù)據(jù)的過程中,為三分量磁場數(shù)據(jù)加入轉向誤差,具體參數(shù)設定如表1所示。把模擬三分量磁場數(shù)據(jù)帶入式(11),對轉向誤差參數(shù)進行估算,估算結果如表1所示。

表1 設定誤差參數(shù)與估算誤差參數(shù)的對比Table 1 Comparison between setting error parameters and estimating error parameters
通過對比表1中的誤差參數(shù)估算值和設定值,可發(fā)現(xiàn)估算值在很大程度上逼近了設定值,零偏誤差、非正交誤差和標度系數(shù)誤差的估算精度分別達到了10-1、10-3和10-4量級。
把轉向誤差參數(shù)估算結果帶入式(3),對模擬磁場數(shù)據(jù)做轉向差校正,校正前后的總場模值曲線對比如圖2所示。校正前,總場模值隨傳感器姿態(tài)變化而上下波動,最大值為50260nT,最小值為49770nT,波動范圍達到490nT,均方根誤差為144.39nT;校正后,總場模值曲線十分平滑,最大值為50002nT,最小值為49999nT,波動范圍降至3nT,均方根誤差降至1.43nT。通過對比校正前后的總場模值曲線,證實了上述算法對轉向差的校正效果良好。
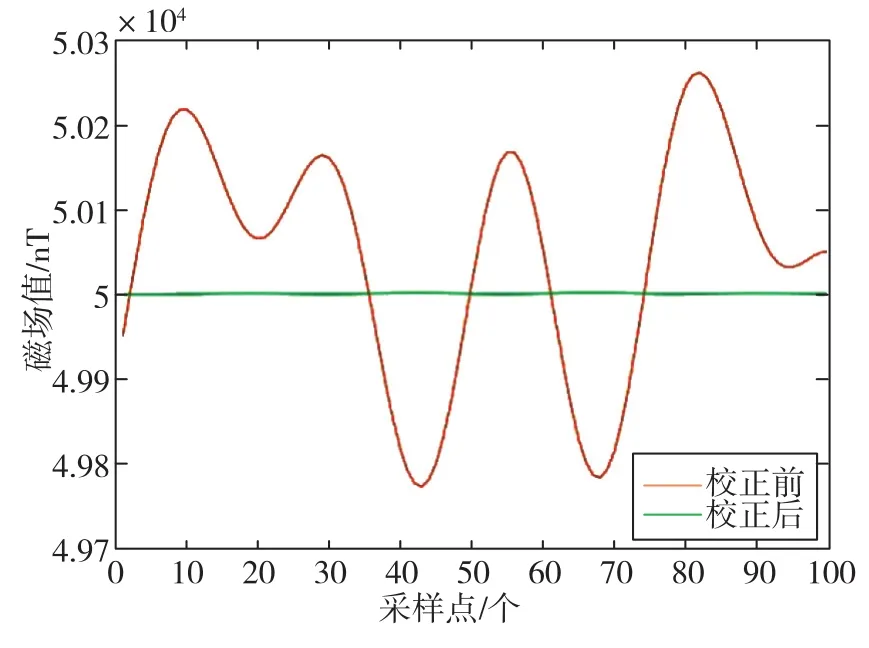
圖2 仿真磁總場模值曲線校正前后對比Fig.2 Comparison of modal curves of simulated total magnetic field before and after correction
為了驗證算法對磁場分量的校正效果,將校正后的磁場分量值與磁場分量真實值(模擬產(chǎn)生的不含誤差的磁場分量)做差,可得到磁場分量差值曲線如圖3所示。可以看出,校正后的磁場各分量與真實磁場分量的差值小于2.2nT,這說明上述算法對磁場分量的校正效果同樣良好。
3 實驗及結果分析
圖3 仿真磁場分量校正前后的差值曲線Fig.3 Simulated difference curve of magnetic field component before and after correction
實驗設備為國產(chǎn)HSF型三軸磁通門傳感器,搭配數(shù)字采集模塊、上位機和離子電池。磁通門傳感器的量程為-100μT~+100μT,標稱正交度≤±0.2°。實驗地點選擇在了遠離工業(yè)與民用設施較少的某海島偏僻處,當?shù)卮艌鲚^為穩(wěn)定、干擾少。在實驗區(qū)域,選擇的兩個點相距約500m,一處作為實驗點,另一處作為對比點。
3.1 實驗點測試
在實驗點,將三軸磁通門傳感器分別繞X軸、Y軸、Z軸勻速轉動,記錄下傳感器的輸出值。利用本文提出的算法對實測磁場數(shù)據(jù)進行計算,得出轉向差參數(shù),具體參數(shù)如表2所示。利用計算出的誤差參數(shù)對當前實測磁場數(shù)據(jù)進行校正,校正前后的總場模值曲線對比如圖4所示。校正前,總場模值隨姿態(tài)變化出現(xiàn)了劇烈波動,出現(xiàn)了明顯的轉向差,總場模值最大為52424nT,最小為52051nT,波動范圍達 373nT,標準差為108.08nT;校正后,總場模值最大為52249nT,最小為52198nT,波動范圍降至51nT,標準差降至8.08nT。可以看出,經(jīng)過校正后,總場模值獲得了極大改善。除了少數(shù)波動尖峰外,數(shù)據(jù)總體比較平滑,轉向差得到了良好的抑制。

表2 計算獲得的轉向誤差參數(shù)Table 2 Calculated diversionary error parameters
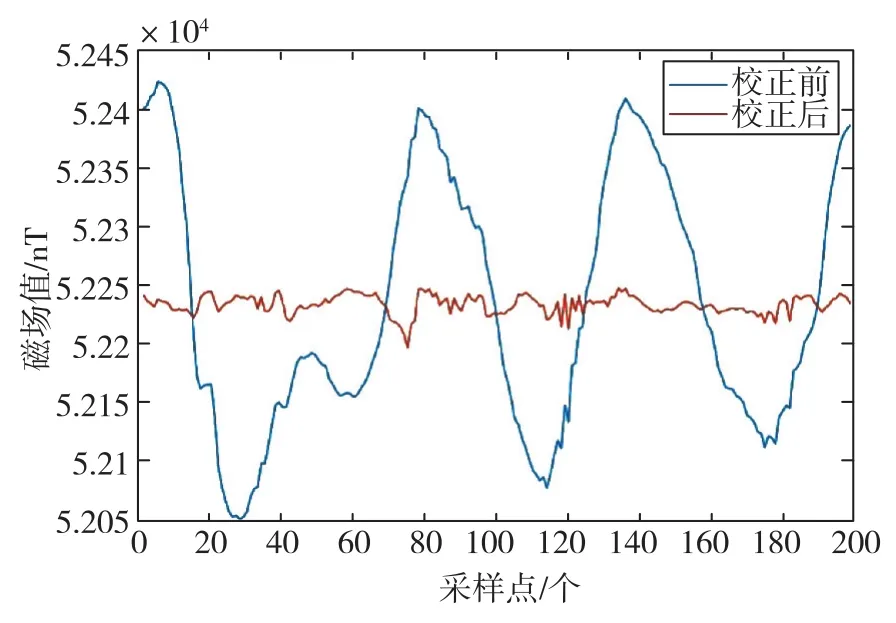
圖4 實驗點數(shù)據(jù)1總場模值校正前后對比Fig.4 Comparison of total field modulus of experiment point data 1 before and after correction
為了驗證上述實驗獲得轉向差參數(shù)的適用性,在實驗點另外采集了一組磁場數(shù)據(jù)。在采集時,令傳感器在空中自由轉動,利用已有轉向差參數(shù)對本次實測數(shù)據(jù)進行校正,校正前后的總場模值曲線對比如圖5所示。可以看出,磁場數(shù)據(jù)在經(jīng)過校正后,總場模值同樣獲得了明顯改善,總場模值波動從352nT降至60nT。經(jīng)計算,總場模值標準差從107.76nT降至15.52nT,校正效果良好。
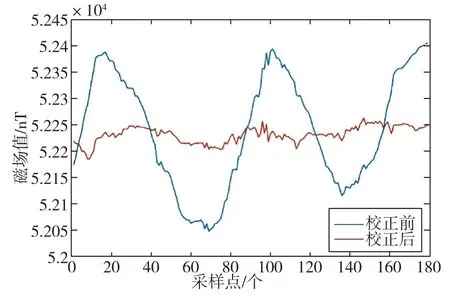
圖5 實驗點數(shù)據(jù)2總場模值校正前后對比Fig.5 Comparison of total field modulus of experiment point data 2 before and after correction
3.2 對比點驗證
為了驗證轉向差參數(shù)的通用性,在對比點進行了磁場數(shù)據(jù)采集。在采集過程中,同樣令磁通門傳感器在空中自由轉動。對比點與實驗點的磁場環(huán)境會有所差異,通過此項實驗可檢驗轉向差參數(shù)對不同磁場環(huán)境下實測數(shù)據(jù)的校正效果,即驗證轉向差參數(shù)的通用性。圖6為校正前后總場模值曲線,校正后的數(shù)據(jù)獲得了明顯改善,總場模值波動從355nT降至79nT,總場模值標準差由103.31nT降至20.82nT,校正效果良好,證明了轉向差參數(shù)具有良好的通用性。
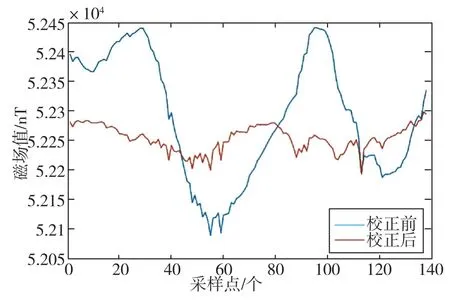
圖6 對比點數(shù)據(jù)總場模值校正前后對比Fig.6 Comparison of total field modulus of comparison point data before and after correction
4 結論
矢量磁力測量具有傳統(tǒng)標量磁力測量不可比擬的優(yōu)勢,但三軸磁通門傳感器轉向差的存在影響了其測量精度。本文在分析了轉向差產(chǎn)生機理的基礎上,建立了誤差參數(shù)估算模型,通過最小二乘法估算出了誤差參數(shù),進而對磁測數(shù)據(jù)進行了轉向差校正。仿真計算結果表明,模型對誤差參數(shù)估算準確,對轉向差的校正效果良好。利用三軸磁通門傳感器進行了磁場測量實驗,結果表明,模型可以估算出實際傳感器的誤差參數(shù),對實測數(shù)據(jù)的轉向差抑制效果達到了90%以上。通過對比點實驗,亦證明了誤差參數(shù)具有良好的通用性。綜合來看,該算法簡單高效,可以明顯抑制轉向差,提高矢量磁測精度,具有很強的實用價值。

