重力傳感器參數雙軸旋轉調制標定方法及實驗驗證
楊柏楠,曹聚亮,于瑞航,蔡劭琨
(國防科技大學智能科學學院,長沙410073)
0 引言
航空重力測量是一種以飛機為載體,利用航空重力儀等設備獲取地球重力場信息的重力測量方法[1]。高精度的重力場信息是研究地質構造和勘探礦產資源不可或缺的重要信息[2],捷聯式航空重力儀是一種經典的用于獲取高精度重力數據的實驗儀器[3]。
捷聯式航空重力儀的核心是一套慣性/衛星組合導航系統,因此在衛星導航精度一定的前提下,由捷聯式重力測量的基本原理可知,加速度計敏感的比力測量精度將較大地影響重力測量的精度[4]。在器件精度難以提高的情況下,傳感器參數估計的效果直接決定了器件能否充分發揮其潛力。在進行重力測量的過程中,加速度計參數通常直接采用在實驗室條件下標定出的傳感器參數。由于慣性器件的自身特性,傳感器參數存在逐次啟動不重復性誤差,這對于高精度的重力測量而言,會降低重力測量的精度。因此,采用合適的方法對加速度計的參數進行外場標定很有必要。雙軸旋轉平臺令系統進行有規律的轉位運動,可在無水平和方位基準的條件下,實現加速度計在靜止載體上的標定[5]。因此,引入雙軸旋轉平臺,可使捷聯式重力儀在外場環境中進行參數估計。
本文以靜態條件下的加速度計參數模型為基礎,采用全局可觀性方法對系統的可觀性進行了分析,得到了參數完全可觀的條件,并以此設計了標定方案[6]。利用有限位的雙軸旋轉平臺對標定方法進行驗證,設計編排方案,對加速度計參數進行了估計,并對實驗結果進行了分析,給出了結論。
1 靜態多位置可觀性分析
在靜態條件下,加速度計的測量值與輸出值的關系可表示為[7]

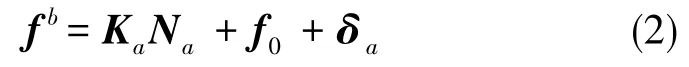
式(2)中,Ka為加速度計的刻度因數,Na為加速度計輸出的脈沖,f0為加速度計零偏,δa為加速度計的噪聲。將式(2)代入式(1),然后對其取模求平方,可得
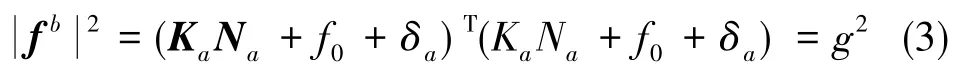
化簡可得
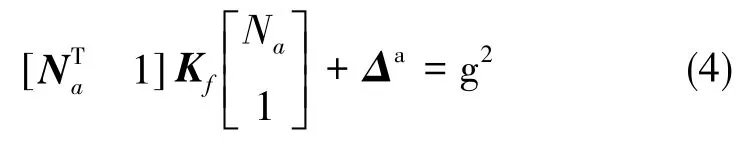
設
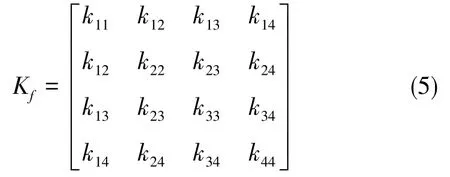
可將式(4)整理為如下形式
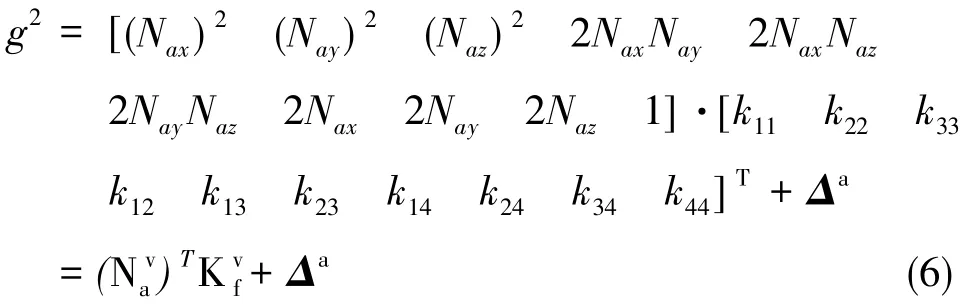
假設存在m(m≥10)個靜態位置的輸出,則有
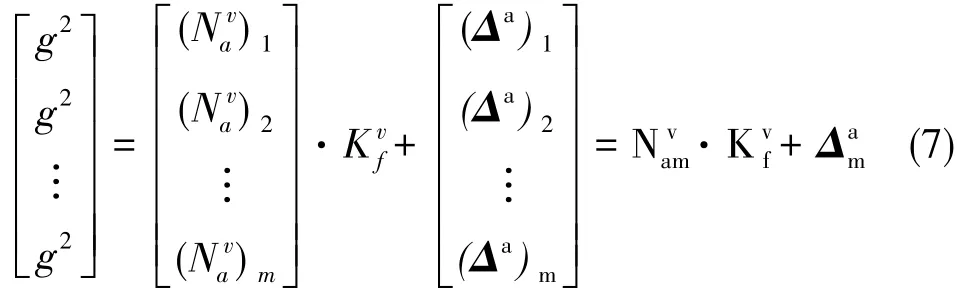
在各加速度計的刻度因子符號已知的情況下,如果加速度計零偏滿足,則足夠多的靜態測試位置(m≥9)可保證加速度計測量組成的矩陣列滿秩,詳細推導過程見文獻[8]。綜上所述,當存在足夠多的靜態位置(m≥9)時,加速度計的參數可觀。
2 編排方案設計
根據上文中靜態多位置可觀性分析的結果,當存在足夠多的靜態位置,即滿足條件時,理論上可以對加速度計的標度因數和零偏進行估計。在實際設計編排方案時,需要通過轉臺為標定提供足夠多的位置,使得上述條件得到滿足。
根據實驗室現有設備,選用有限位的雙軸平臺作為實驗轉臺,其實物圖及重力儀如圖1所示。

圖1 雙軸平臺及重力儀Fig.1 Biax platform and gravimeter
實驗室所用的重力儀采用了前上右的載體坐標系,它的x軸與平臺的內框旋轉軸重合,z軸與平臺的外框旋轉軸重合,平臺不存在繞天向軸的角運動。
該雙軸旋轉平臺的性能參數如表1所示,其在俯仰和橫滾方向上只能實現-30°~+30°之間的角運動。在進行標定路徑編排設計時,需要該平臺的性能參數及標定加速度計所需滿足的條件。
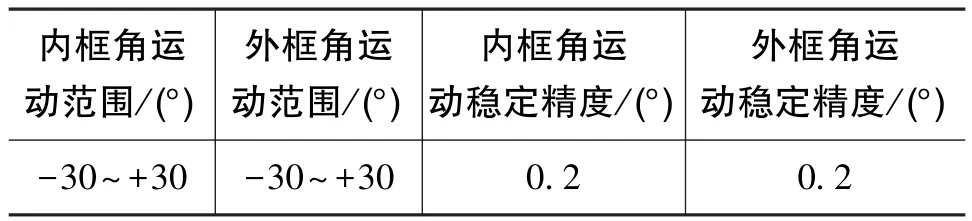
表1 雙軸旋轉平臺的性能參數Table 1 Performance parameters of biax rotating platform
充分利用雙軸平臺的可旋轉角度,通過俯仰和橫滾方向上的角運動,使得加速度計與重力矢量之間的相對位置足夠多,則可對加速度計的參數進行標定。由于所用平臺為雙軸旋轉平臺,重力儀在天向軸方向上不存在角運動,因此在設計編排標定路徑時,僅需考慮水平兩個軸的角運動。在路徑表中,“+”表示正向旋轉,“-”表示反向旋轉,數字代表所需旋轉的角度。例如,(+30°,+30°)表示繞內框正向旋轉30°和繞外框正向旋轉30°,如圖 2(a)所示;而(+30°,-30°)表示繞內框正向旋轉30°和繞外框負向旋轉 30°,如圖2(b)所示。
具體標定路徑如表2所示。

圖2 旋轉后的平臺實物圖Fig.2 Drawing of the platform after rotation

表2 標定路徑編排Table 2 Layout of calibration path
對于所設計的標定路徑能否滿足傳感器參數估計的要求,需要進行理論計算并與上文中提到的靜態多位置可觀的條件進行比較。假設,在位置1時(轉臺零位時),加速度計所測得的重力理論值為正常重力,即fb=[0-g0]T,那么可以由此給出其他位置的加速度計的理論輸出;在位置2時(相對位置1內框旋轉+30°),其理論輸出為;在位置3時(相對位置2外框旋轉+30°),其理論輸出為;在位置4時(相對位置3外框旋轉-60°),其理論輸出為。同理,可以計算其他位置的加速度計理論輸出。其中,g為標準重力值。將加速度計的理論輸出作為其實際的脈沖輸出,計算矩陣,得到

綜上所述,上文所設計的標定路徑可以對加速度計的參數進行估計,并滿足實驗要求。
3 實驗及分析
在常溫下,對某型光纖陀螺捷聯式重力儀進行標定測試,所用重力儀如圖1所示,標定所用路徑如表2所示,共有17個靜態位置,每個位置采樣100s。
將重力儀按指定方式安裝在雙軸旋轉平臺上,然后控制內框和外框按上文中所設計的標定路徑進行轉動,記錄下各軸加速度計的脈沖輸出,具體如圖3所示。
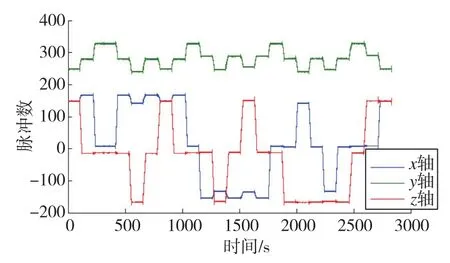
圖3 3個軸的加速度計輸出Fig.3 Output of three-axes accelerometer
通過對輸出脈沖進行數據截取,去除加速度計在旋轉過程中的脈沖,以此用于加速度計的參數估計[9]。以模標定算法[8]為基礎,結合雙軸平臺的相關特點,對算法進行改進,可以得到加速度計參數的估計值,結果如表3所示。
以第1組實驗為例,Ka對角線上元素與參考標定結果的最大偏差為8.61607×10-8,對應的傳感器刻度因子偏差為 8.61607×10-8/(1.515979×10-4)=565×10-6,而非對角線上元素的最大誤差為1.80993×10-6。從此結果來看,在對傳感器的刻度因數進行估計時,各加速度計的刻度因子估計效果較好,而3個加速度計之間的安裝誤差則估計較差,加速度計的零偏估計也較差。
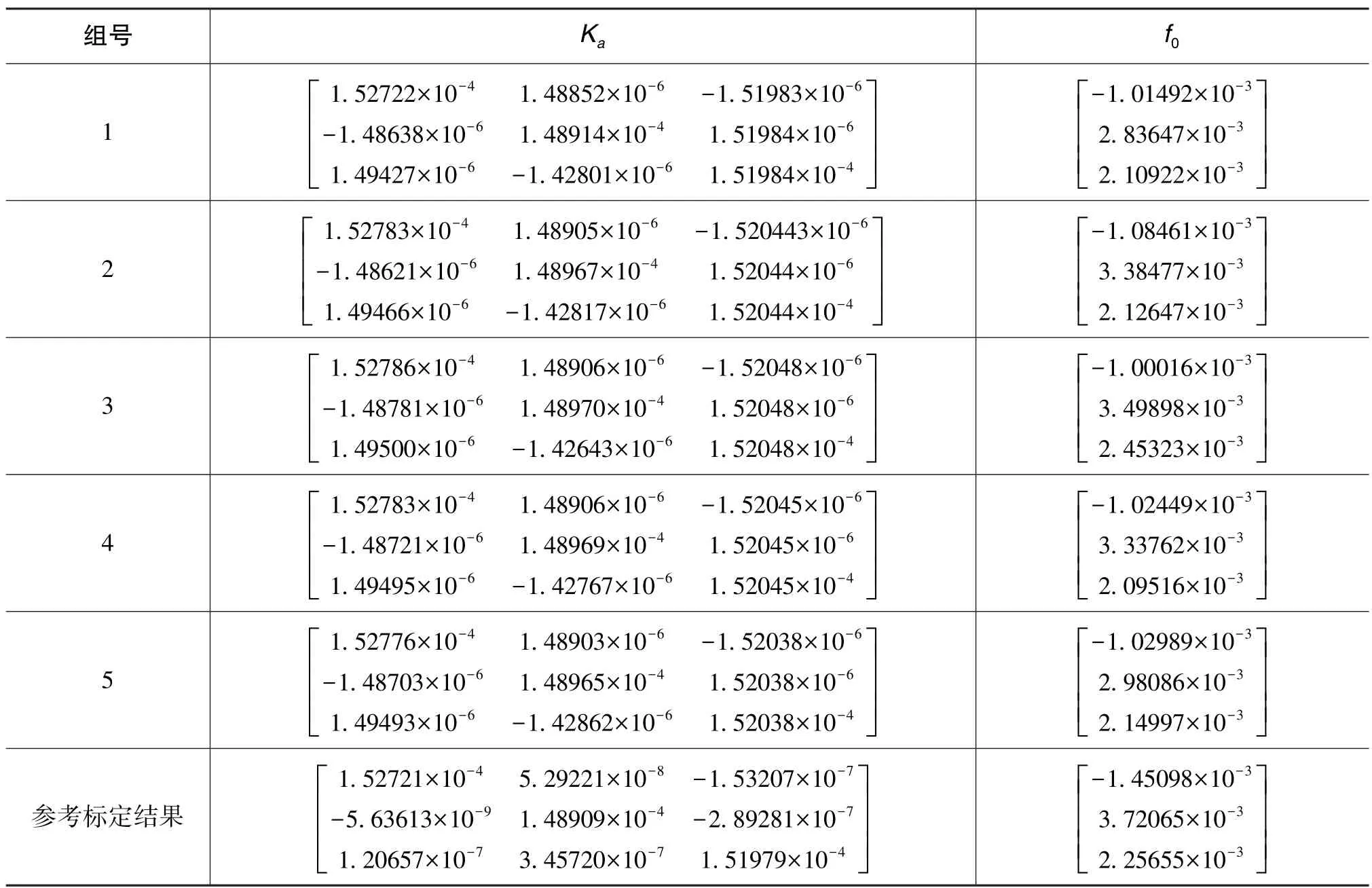
表3 標定實驗結果及參考標定結果Table 3 Results of calibration experiment and reference calibration
此次實驗對安裝誤差和零偏的估計值精度略差,這可能源于以下幾個原因:首先,在此次實驗中,轉臺的角位置精度指標為0.2°,轉臺精度誤差使得加速度計之間的安裝誤差被掩蓋,非對角線上的估計值可能包含轉臺的非正交誤差,轉臺精度誤差也導致其靜態位置難以保證足夠的精度,使得零偏的測量出現較大的誤差;其次,通過位置靜態測量,難以激勵出安裝誤差;最后,在進行外場實驗時,缺乏實驗室的減震降噪條件,而在實驗過程中靜止時間較短,難以通過濾波的方法平滑噪聲。下面,重點對加速度計的刻度因數進行研究。
針對上文中安裝誤差估計值精度較低的問題,提出如下解決思路。根據文獻[8],加速度計的線性脈沖輸出模型如下

式(9)中,[NaxNayNaz]T為采樣時間T的脈沖輸出,為各個加速度計輸入與輸出的比例關系,矩陣為安裝關系。假設安裝誤差角為小角度,可將式(9)化簡為
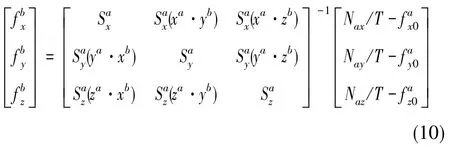
由式(9)可知,各加速度計的刻度因子與安裝關系之間不相關,若安裝關系矩陣已知,求解刻度因子,然后用矩陣運算計算加速度計的刻度因數。加速度計的外場標定是充分利用已知條件對加速度計的部分參數進行的重新標定,而不是在實驗室條件下的全參數標定;加速度計之間的安裝誤差是由重力儀出廠過程中的制作工藝導致的,因此在重力儀的使用過程中,加速度計之間的安裝關系基本不變。
綜上所述,為解決外場標定中安裝誤差估計精度較差的問題,可利用實驗室三軸轉臺標定出安裝關系,然后將此結果用于重力儀的外場標定。表4為采用此方法的改進后的刻度因數。
以第1組為例,改正后的非對角線元素精度提高了10~103量級,其非對角線元素與參考結果的最大偏差為 1.95997×10-10,則 1.95997×10-10/(3.45720×10-7)=567×10-6,與對角線的刻度因子偏差精度相當。因此,此改進方法較好地解決了安裝誤差估計精度較差的問題。
截取一段處于水平位置的靜態測量數據,分別使用第1組外場標定的加速度計參數和實驗室三軸轉臺標定的加速度計參數進行純慣導解算,其結果如圖4所示。
從2800s的導航解算結果來看,本文所用方法的經度誤差略優于實驗室三軸轉臺的標定效果,而在緯度誤差方面兩者則基本一致;從運動軌跡來看,本文所用方法也略優于實驗室標定;具體到導航解算的位置誤差,經過2800s的純慣性導航,本文所用方法使得導航精度提高了14m。綜上所述,本文所用標定方法與實驗室三軸轉臺標定方法的純慣性導航精度相當,證明了對加速度計進行外場參數估計,可在一定程度上改善重力測量的精度。
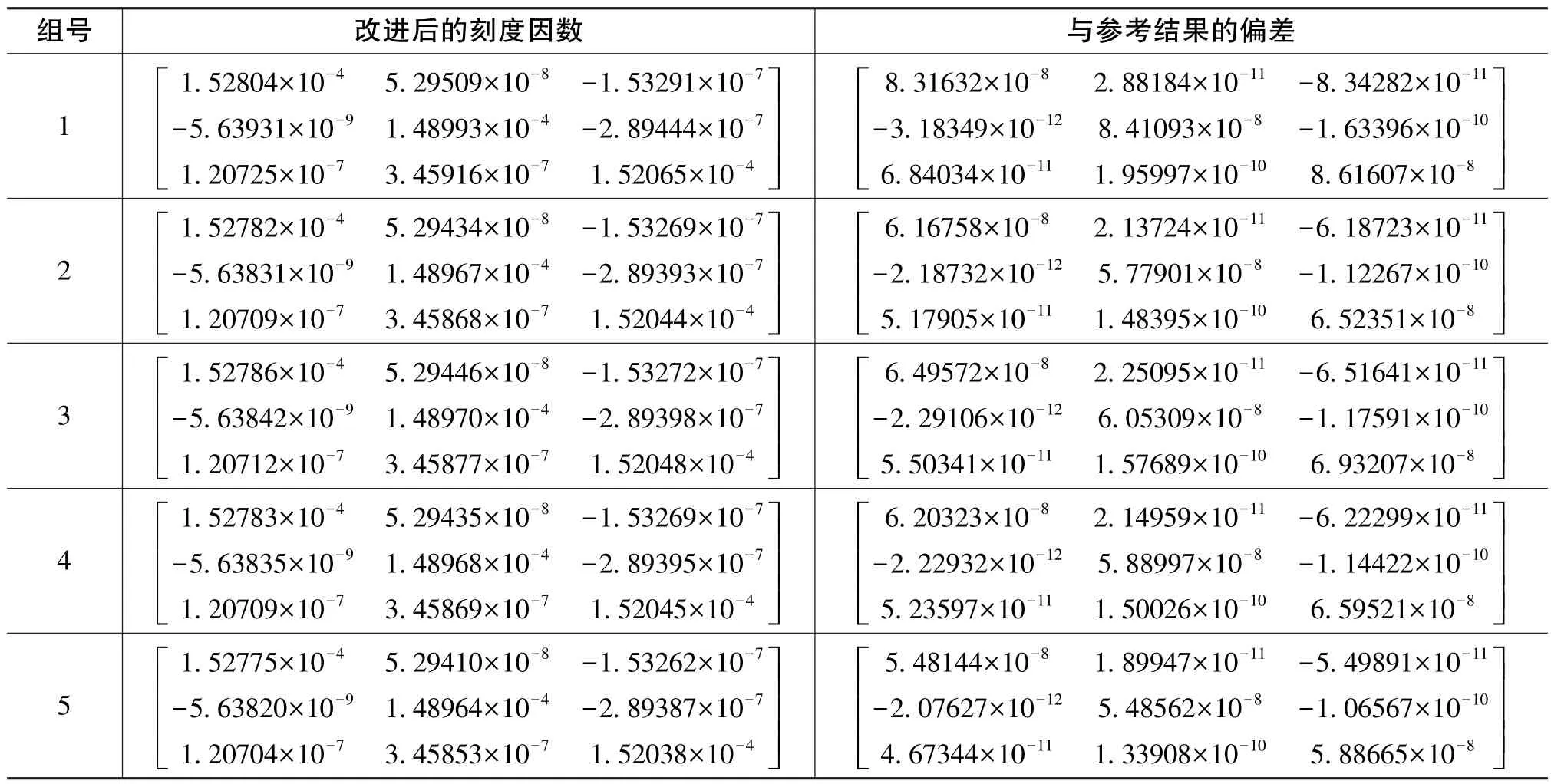
表4 改進后的Ka標定結果Table 4 Improved calibration results of Ka
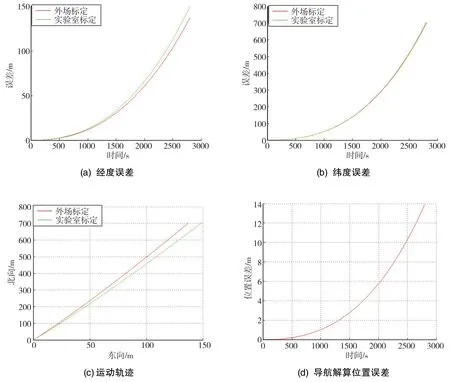
圖4 純慣性導航結果對比Fig.4 Results comparison of pure inertial navigation
4 結論
從以上的分析和實驗結果來看,引入雙軸旋轉平臺,采用對轉臺要求的標定算法,可以較為精確地估計加速度計的刻度因數,在一定程度上減少了重力儀逐次啟動不重復性誤差,提高了重力儀的測量精度。當然,在零偏的估計上還存在一定的問題,雙軸旋轉平臺的精度需要提高,需降低由轉臺相關誤差帶來的影響。在靜態測量時,可采用以時間換精度的策略,通過長時間的測量來平滑噪聲。

