基于閾值自適應憶阻器Hopfield神經網絡的關聯規則挖掘算法

于永斌 戚敏惠 尼瑪扎西 王琳

摘 要：針對基于Hopfield神經網絡的最大頻繁項集挖掘 （HNNMFI）算法存在的挖掘結果不準確的問題，提出基于電流閾值自適應憶阻器（TEAM）模型的Hopfield神經網絡的改進關聯規則挖掘算法。首先，使用TEAM模型設計實現突觸，利用閾值憶阻器的憶阻值隨方波電壓連續變化的能力來設定和更新突觸權值，自適應關聯規則挖掘算法的輸入。其次，改進原算法的能量函數以對齊標準能量函數，并用憶阻值表示權值，放大權值和偏置。最后，設計由最大頻繁項集生成關聯規則的算法。使用10組大小在30以內的隨機事務集進行1000次仿真實驗，實驗結果表明，與HNNMFI算法相比，所提算法在關聯挖掘結果準確率上提高33.9個百分點以上，說明憶阻器能夠有效提高Hopfield神經網絡在關聯規則挖掘中的結果準確率。

關鍵詞：電流閾值自適應憶阻器;Hopfield神經網絡;最大頻繁項集;關聯規則挖掘;能量函數

中圖分類號： TP301.6

文獻標志碼：A

文章編號：1001-9081（2019）03-0728-06

Abstract： Aiming at the inaccurate mining results of the Maximum Frequent Itemset mining algorithm based on Hopfield Neural Network （HNNMFI）， an improved association rule mining algorithm for Hopfield neural network based on current ThrEshold Adaptive Memristor （TEAM） model was proposed. Firstly， TEAM model was used to design and implement synapses whose weights were set and updated by the ability of that threshold memristor continuously changes memristance value with square-wave voltage， and the input of association rule mining algorithm was self-adapted by the neural network. Secondly， the energy function was improved to align with standard energy function， and the memristance values were used to represent the weights， then the weights and bias were amplified. Finally， an algorithm of generating association rules from the maximum frequent itemsets was designed. A total of 1000 simulation experiments using 10 random transaction sets with size less than 30 were performed. Experimental results show that compared with HNNMFI algorithm， the proposed algorithm improves the result accuracy of association mining by more than 33.9 %， which indicates that the memristor can effectively improve the result accuracy of Hopfield neural network in association rule mining.

Key words： current ThrEshold Adaptive Memristor （TEAM）; Hopfield Neural Network （HNN）; maximum frequent itemset; association rule mining; energy function

0 引言

憶阻器的概念由蔡紹棠教授在1971年提出[1]，2008年惠普實驗室的研究人員Strukov等[2]首次做出實物模型，此后掀起憶阻器的研究熱潮。憶阻器具有非線性和記憶特性[3]，用來模擬人工神經網絡中的突觸[4]，能夠實現突觸權值的連續更新并且在斷電之后也能保存權值。近年來，許多憶阻器的數學模型相繼被提出，其中Kvatinsky等提出電流閾值自適應憶阻器（ThrEshold Adaptive Memristor， TEAM）模型[5]，該模型可通過調整系數以匹配其他憶阻器的數學模型，是一種非常精確且很有潛力的數學模型[6]。目前憶阻器的國內外研究方向主要包括神經網絡、存儲器、混沌電路、交叉陣列等[7]。憶阻器在神經網絡中的研究取得很多進展[8-10]，如電子科技大學的Hu等使用可重構憶阻離散Hopfield神經網絡實現單聯想和多聯想記憶[11]。

Hopfield神經網絡（Hopfield Neural Network， HNN）由Hopfield等在1982年提出，該模型又分為離散型（Discrete Hopfield Neural Network， DHNN）[12]和連續型（Continuous Hopfield Neural Network， CHNN）[13]。能量函數的概念被首次引入到人工神經網絡中，為解決優化計算問題提供新的方法。能量函數的標準形式已由Hopfield給出，不同的優化問題對應的能量函數形式不同，但都由約束條件和目標解兩個部分組成，只要能將其轉化為標準形式便可從能量函數中導出權重和偏置。CHNN隨時間演變，始終向能量函數降低的方向移動，最后達到能量函數的極小值點，即穩定平衡狀態。將優化問題的目標函數與網絡的能量函數相對應，則問題的求解過程可以看作CHNN向能量函數極小值點移動的過程。目前HNN的應用領域主要包括聯想記憶和優化計算等[13]。

關聯規則的概念最初是Agrawal等[14]在1993年針對購物籃分析問題（Market Basket Analysis）提出的，且于1994年提出經典的關聯規則挖掘算法Apriori算法[15]。目前常見的關聯規則挖掘算法[16]大致可分為：寬度優先算法如DHP（Direct Hashing and Pruning）算法[17];深度優先算法如FP-growth（Frequent-Pattern growth）算法[18];數據集劃分算法如Partition算法[19];采樣算法如Sampling算法[20];并行挖掘算法如CD（Count Distribution）、DD（Data Distribution）、CaD算法（Candidate Distribution）[21]等。其中FP-growth算法對Apriori算法的改進效果最顯著。

Gaber等[22]提出基于Hopfield神經網絡的最大頻繁項集挖掘 （Maximum Frequent Itemset mining based on Hopfield Neural Network， HNNMFI） 算法，該算法屬于并行挖掘算法，為CHNN在關聯規則挖掘領域中的應用提供可行的思路。但該算法定義的能量函數與標準形式不太符合，權值和偏置較小，導致挖掘到的頻繁項集范圍小，無法適應不同大小的事務集。

本文針對上述問題，提出基于憶阻Hopfield神經網絡（Memristive Hopfield Neural Network， MHNN）的關聯規則算法，主要貢獻概括如下：

1）提出改進的MHNN。

MHNN使用憶阻器和電阻組成的分壓電阻作為突觸，通過開關陣列實現正負突觸權值的選擇。該網絡不僅結構簡單，而且能夠自適應關聯規則挖掘算法的事務矩陣。

2）提出新的基于MHNN的關聯規則挖掘算法。

新算法對HNNMFI算法的能量函數、權值以及偏置進行了修改，并設計由最大頻繁項集生成關聯規則的算法，在軟件仿真上能夠有效提高關聯規則挖掘結果準確度。

1 基本概念

1.1 TEAM模型

TEAM模型對Abdalla等[23]提出的Simmons隧道結模型進行簡化，不僅保留Simmons模型準確捕捉閾值的特點和簡化Simmons模型的數學表達式，還可通過調整系數以匹配其他憶阻器的數學模型，是一種非常精確且具有潛力的數學模型。該模型的狀態變量微分方程、窗函數表達式和憶阻值表達式[5]分別如下：

本文只考慮TEAM模型的憶阻值為線性關系，如式（4）所示。在外部電流正弦信號5sin（2πt）mA的激勵下，對TEAM模型按照表1的參數設定進行代碼仿真，得到圖1的仿真結果。

圖1（a）是外部正弦電流信號的波形圖，從圖1（c）中可以看出，正向電流得到更大電壓，驗證了TEAM模型的開關變化的非對稱性。向該模型中加入圖1（d）所示窗函數后，得到了圖1（b）所示憶阻值隨時間變化的曲線，從圖1（b）中可以看出，在電流未達到閾值電流ioff 時，憶阻值保持不變，達到之后憶阻值開始變化。

重新調整TEAM模型的參數，為TEAM模型輸入幅值為2V，周期為1s的方波電壓，保證此時通過憶阻器的電流大于閾值電流ioff，能夠使憶阻值發生改變。從仿真結果中可以得出憶阻值隨方波電壓連續變化，且成上升趨勢，說明方波電壓對TEAM模型憶阻器起到阻值編程作用，使TEAM模型憶阻器非常適合作電子突觸。

1.2 CHNN基本結構

DHNN和CHNN的區別在于神經元輸出不同，前者是二值的網絡，神經元的取值為{0，1}或{-1，1}，后者的神經元輸出在某個區間內連續取值。本文只針對CHNN進行分析，網絡中神經元的輸入和輸出之間呈現sigmoid函數關系[13]，該函數的一種常見表達形式[22]如下：

的連接權重;E（v）是能量函數。Hopfield網絡解決組合優化問題的步驟為：

1）對于待求解的問題，提供一種合理的解釋方案能夠使網絡的輸出表示被求解問題的解。

2）構造能量函數，使能量函數對應被求解問題的目標函數，能量函數向極小值點移動的過程就是問題的求解過程。

3）從能量函數中導出權重Tij和偏置電流Ii。

4）運行Hopfield神經網絡，當網絡達到穩定狀態時的輸出就是一定條件下問題的最優解。

1.3 關聯規則挖掘基本概念

定義2 支持度。規則XY的支持度為X和Y在D的每個事務中一起出現的概率，記為support（XY）=P（XY）。

定義3 置信度。規則XY的置信度表示為D中包含項集X的事務中項集Y的百分比，即項集Y出現的條件概率，記作confidence（XY）=P（Y|X）。

定義4 頻繁項集。若項集X的支持度大等于用戶定義的最小支持度，則稱X為頻繁項集，否則稱X為非頻繁項集。

定義5 最大頻繁項集。如果頻繁項集X上的所有超集都不是頻繁項集，則稱X為局部最大頻繁項集，所有局部最大頻繁項集組成的集合稱最大頻繁項集。

關聯規則挖掘算法遵循兩個步驟[24]：第一步是找到所有的頻繁項集;第二步是在上一步的基礎上產生關聯規則。考慮到最大頻繁項集已經隱含所有頻繁項集信息，因此本文只需考慮挖掘最大頻繁項集問題。

2 基于HNN的最大頻繁項集挖掘算法

2.1 網絡結構設計

HNN的神經元分布同事務矩陣D一樣，共有n*p個神經元且呈二維數組形式排列。由于每個神經元接收到的突觸數量都是一樣的，因此該網絡可抽象為1行n*p列的單層網絡結構。以一個具有2行3列神經元的HNN為例，本文設計的HNN結構如圖2所示。

2.2 確定最大頻繁項集

本文對Gaber等提出的HNNMFI算法的能量函數進行修改：首先為了同能量函數的標準式對齊，將原能量函數的第二項（偏置部分）前面的符號由加變為減;其次，將第三項中k的累加上限由p改為n。修改后的能量函數能夠適用大小不同的事務集，而原能量函數只能適用行數（n）和列數（p）相同的事務集，修改后的能量函數定義如下：

其中：A、B和C是正的常數，代表各個約束項的重要程度，n和p分別代表事務數和項目數，VTi代表第T筆事務中第i個神經元的輸出，min是用戶定義的最小支持度，bTi表示項目i是否出現在第T筆事務中，是為1，否為0。公式中的前兩項確保每行生成一個有效解，該解具有該行表示事務包含的最大項集，第三項確保輸出的解是頻繁項集，即該解的支持度大于用戶定義的最小支持度。

根據圖2（a）所示結構，將下標T用A，B代替，重寫（6）、（7）和（8）得：

網絡參數的選取將會影響網絡的效率以及結果準確性，目前對于網絡參數的選擇尚無理論依據。在實驗和經驗的基礎上，HNN的參數設定如表2所示。

由于網絡的迭代次數和步長與事務集所得的權值矩陣有關，使用多個事務集對HNN進行測試后在實驗的基礎上，總結出網絡的權值矩陣同迭代次數Count和步長step的關系如下，其中x是權值矩陣中絕對值最大數的指數。

從能量函數中得到權重和偏置以及確定網絡參數后，按照第1章提出的HNN求解組合優化問題的步驟，只需建立并運行HNN，等網絡達到穩定狀態，便可以求解出最大頻繁項集，具體描述如算法1所示。

使用表3所示的事務集對該算法進行測試，minSup和minConf均設置為0.5，網絡的迭代次數Count和步長step由式（14）計算后分別為500和10-5，按照算法1流程運行網絡，得到編碼規則數組code為{beer，bread，cook，diaper，egg，milk}，110101，V使用code翻譯出來是{beer，bread，diaper，milk}，而使用Apriori算法得到的最大頻繁項集是{{beer，bread}，{beer，diaper}，{beer，milk}，{diaper，milk}}。可見HNNMFI算法得到的最大頻繁項集是定義5中的所有局部最大頻繁項集的并集。

3 基于MHNN的最大頻繁項集挖掘算法

3.1 電路結構設計

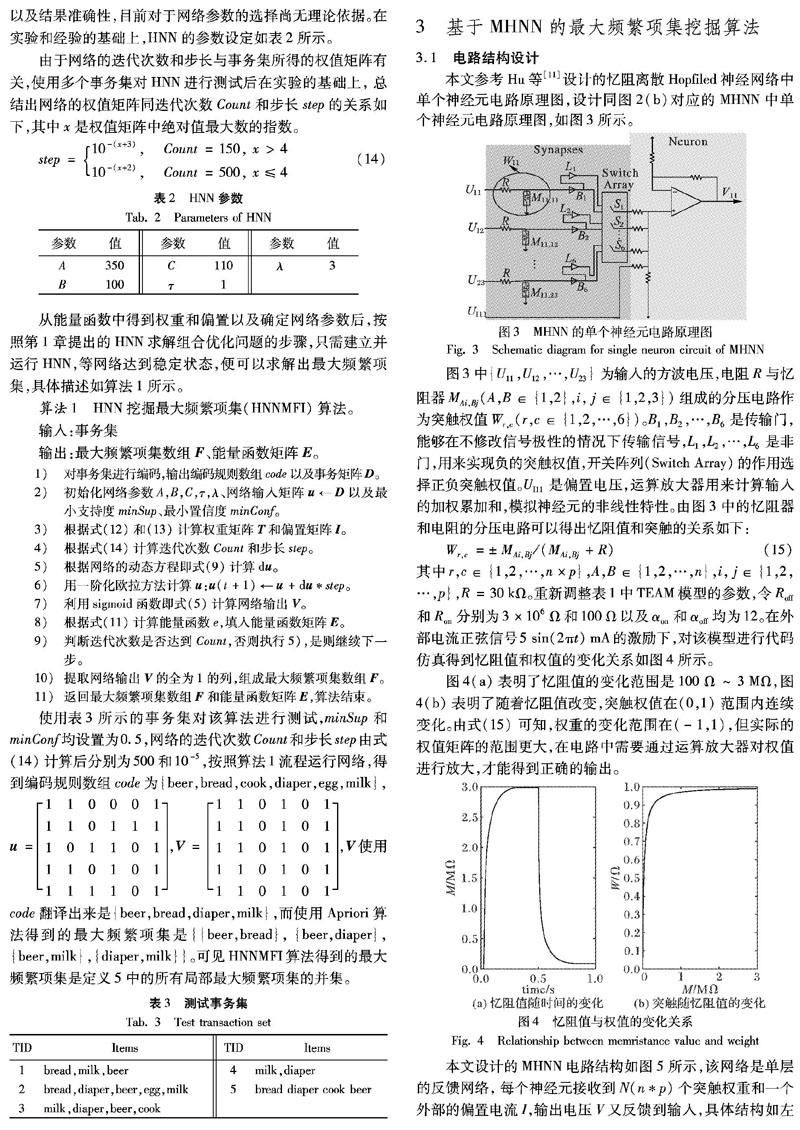
本文參考Hu等[11]設計的憶阻離散Hopfiled神經網絡中單個神經元電路原理圖，設計同圖2（b）對應的MHNN中單個神經元電路原理圖，如圖3所示。

圖4（a）表明了憶阻值的變化范圍是100Ω～3MΩ，圖4（b）表明了隨著憶阻值改變，突觸權值在（0，1）范圍內連續變化。由式（15） 可知，權重的變化范圍在（-1，1）之間，但實際的權值矩陣的范圍更大，在電路中需要通過運算放大器對權值進行放大，才能得到正確的輸出。

本文設計的MHNN電路結構如圖5所示，該網絡是單層的反饋網絡，每個神經元接收到N（n*p）個突觸權重和一個外部的偏置電流I，輸出電壓V又反饋到輸入，具體結構如左邊大的最深色陰影部分所示，該部分也是圖3的擴展。

3.2 突觸權值和偏置的映射

本文的MHNN主要是通過軟件仿真實現的，為了對應圖5的單個神經元電路，首先將HNN中的權值矩陣Wrc′按照式（16）進行歸一化，使歸一化之后的權值矩陣范圍在（-1，1）之間。

在對權值矩陣進行歸一化之后，為了保證MHNN挖掘最大頻繁項集算法的結果準確性，還需要將歸一化后的權值矩陣按照式（17）進行放大。

4 最大頻繁項集生成關聯規則算法

本文設計的由最大頻繁項集生成關聯規則的算法分為兩步。第一步生成所有頻繁項集的支持度數組，主要通過最大頻繁項集的組合運算，產生所有的非空子集（子頻繁項集），求出每個子集的支持度，存入支持度數組，具體描述如算法2所示。

第二步從支持度數組中生成滿足用戶定義的最小支持度與最小置信度的關聯規則。首先遍歷支持度數組，取頻繁項集，作為關聯規則XY中的X，再取支持度數組中與X不相交的頻繁項集作為關聯規則的Y，計算XY的支持度和置信度，滿足要求則填入關聯規則，具體描述如算法3所示。

5 仿真實驗結果分析

5.1 設計生成隨機分布事務集算法

由于HNN求解大規模的組合優化問題十分困難，處理小范圍的數據集比較容易，所以本文提出的MHNN目前只適用于小規模的事務集，加上關聯規則挖掘的測試數據集都比較大，不適用于本文的測試，故本文設計生成隨機分布事務集算法來對比兩種網絡的挖掘結果準確率。該算法具體描述如算法4所示，可通過設置傳入事務集的行數n，列數p以及1出現的概率p1來控制隨機生成事務集的大小和疏密程度。

5.2 1000次仿真實驗的關聯規則挖掘結果分析

本文設定算法4的輸入n=p，p1=0.5，最小支持度和最小置信度均設置為0.5。設置10種不同大小的事務集，分別為4，6，8，10，12，14，16，18，20，22。對每種事務集分別使用Apriori算法、HNN和MHNN進行100次實驗， 以Apriori算法的結果為標準，統計兩種網絡的挖掘結果準確率，結果如圖6所示。

從圖6中可以看出，當事務集的大小低于10時，兩種網絡的挖掘結果準確率相差不大，但隨著事務集的增大，兩種網絡的準確率曲線差距均在0.27以上。通過計算兩條曲線差值之和的均值，可得出MHNN在HNN的基礎上提升約35.3個百分點的挖掘結果準確率。在上述情況下，又進行多組實驗，其中最好結果為36%，最壞結果為33.9%，得出改進后的算法在關聯挖掘結果準確率上提高33.9個百分點以上。

6 結語

本文在軟件仿真上為憶阻器在HNN處理關聯規則挖掘的問題中的應用提出了一種可行的思路。本文設計的MHNN能夠處理較小規模的關聯規則挖掘問題，但仍然存在容易陷入局部最優點的問題，后續可以考慮使用遺傳算法對該網絡進行改進。

在硬件實現上，隨著關聯規則挖掘問題復雜度的增加，需要設計的電路的規模也相應增大，對網絡的集成度、能耗以及并行處理能力的要求也越來越高。本文設計的MHNN電路結構可以降低電路設計難度，提高電路自適應關聯規則挖掘算法輸入的能力，可有效解決傳統人工神經網絡的瓶頸。

參考文獻 （References）

[1] CHUA L O. Memristor—the missing circuit element [J]. IEEE Transactions on Circuit Theory， 1971， 18（5）： 507-519.

[2] STRUKOV D B， SNIDER G S， STEWART D R， et al. The missing memristor found [J]. Nature， 2008， 453（7191）： 80-83.

[3] DU C， CAI F， ZIDAN M A， et al. Reservoir computing using dynamic memristors for temporal information processing [J]. Nature Communications， 2017， 8： Article No. 2204.

[4] JO S H， CHANG T， EBONG I， et al. Nanoscale memristor device as synapse in neuromorphic systems [J]. Nano Letters， 2010， 10（4）： 1297-1301.

[5] KVATINSKY S， FRIEDMAN E G， KOLODNY A， et al. TEAM： ThrEshold Adaptive Memristor model [J]. IEEE Transactions on Circuits and Systems I： Regular Papers， 2013， 60（1）： 211-221.

[6] 江之源.基于閾值自適應憶阻模型的分析及應用研究[D].重慶：西南大學，2016：11-12.（JIANG Z Y. Analysis and application research based on threshold adaptive memristor model [D].Chongqing： Southwestern University， 2016： 11-12.）

[7] 代祥光.憶阻神經網絡的應用[D].重慶：重慶大學，2012：1-3.（DAI X G. Application of memristive neural network [D]. Chongqing： Chongqing University， 2012： 1-3.）

[8] ALIBART F， ZAMANIDOOST E， STRUKOV D B. Pattern classification by memristive crossbar circuits using ex situ and in situ training [J]. Nature Communications， 2013， 4（3）： 131-140.

[9] PARK S， SHERI A， KIM J， et al. Neuromorphic speech systems using advanced ReRAM-based synapse [C]// Proceedings of 2013 IEEE International Electron Devices Meeting. Piscataway， NJ： IEEE， 2013： 25.6.1-25.6.4.

[10] ZIEGLER M， SONI R， PATELCZYK T， et al. An electronic version of Pavlov's dog [J]. Advanced Functional Materials， 2012， 22（13）： 2744-2749.

[11] HU S G， LIU Y， LIU Z， et al. Associative memory realized by a reconfigurable memristive Hopfield neural network [J]. Nature Communications， 2015， 6： Article number 7522.

[12] HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities [J]. Proceedings of the National Academy of Sciences of the United States of America， 1982， 79（8）： 2554-2558.

[13] HOPFIELD J J， TANK D W. “Neural” computation of decisions in optimization problems [J]. Biological Cybernetics， 1985， 52（3）： 141-145.

[14] AGRAWAL R， IMIELINSKI T， SWAMI A N. Mining association rules between sets of items in large databases [C]// Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. New York： ACM， 1993：207-216.

[15] AGRAWAL R， SRIKANT R. Fast algorithms for mining association rules in large databases [C]// VLDB '94： Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco， CA： Morgan Kaufmann， 1994： 487-499.

[16] 王愛平，王占鳳，陶嗣干，等.數據挖掘中常用關聯規則挖掘算法[J].計算機技術與發展，2010，20（4）：105-108.（WANG A P， WANG Z F， TAO S G， et al. Common algorithms of association rules mining in data mining [J]. Computer Technology and Development， 2010，20（4）： 105-108.）

[17] PARK J S， CHEN M S， YU P S. An effective hash-based algorithm for mining association rules [J]. ACM SIGMOD Record， 1995， 24（2）： 175-186.

[18] JI C R， DENG Z H. Mining frequent ordered patterns without candidate generation [C]// Proceedings of the 4th IEEE International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway， NJ： IEEE， 2007，1： 402-406.

[19] SAVASERE A， OMIECINSKI E， NAVATHE S B， et al. An efficient algorithm for mining association rules in large databases [C]// VLDB '95： Proceedings of the 21st International Conference on Very Large Data Bases. San Francisco， CA： Morgan Kaufmann， 1995： 432-444.

[20] TOIVONEN H. Sampling large databases for association rules [C]// VLDB '96： Proceedings of the 22th International Conference on Very Large Data Bases. San Francisco， CA： Morgan Kaufmann， 1996： 134-145.

[21] AGRAWAL R， SHAFER J C. Parallel mining of association rules [J]. IEEE Transactions on Knowledge and Data Engineering， 2007， 8（6）： 962-969.

[22] GABER K， BAHI J M， EL-GHAZAWI T A. Parallel mining of association rules with a Hopfield type neural network [C]// ICTAI '00： Proceedings of the 12th IEEE International Conference on Tools with Artificial Intelligence. Washington， DC： IEEE Computer Society， 2000： 90-93.

[23] ABDALLA H， PICKETT M D. SPICE modeling of memristors [C]// Proceedings of the 2011 IEEE International Symposium on Circuits and Systems. Piscataway， NJ： IEEE， 2011： 1832-1835.

[24] 徐開勇，龔雪容，成茂才.基于改進Apriori算法的審計日志關聯規則挖掘[J].計算機應用，2016，36（7）：1847-1851.（XU K Y， GONG X R， CHENG M C. Audit log association rule mining based on improved apriori algorithm [J]. Journal of Computer Applications， 2016， 36（7）： 1847-1851.）