基于灰色理論的ofo 需求量短時預測?

趙廣元 尚秋燕

（西安郵電大學自動化學院 西安 710121）

1 引言

共享單車（ofo）作為2016年城市出現的一種新型共享經濟產物，有效地解決了“最后一公里”的難題，它的一大特色就是尋找、使用、停放實現了隨用隨取、隨停隨放，真正體現了自行車的便利性，滿足了大眾群眾的出行需求。同時，數量日益龐大的共享單車也因為亂停亂放、擠占公共空間等問題給城市管理帶來了新的挑戰［1～2］。在不改變既有的城市規劃格局條件下，對ofo需求量的科學有效預測，對相應指標體系的制定（如規范ofo車輛投放秩序）起著越來越重要的作用。

短時預測方法經過幾十年的研究已超過200種，基本可分為基于線性系統理論、基于非線性系統理論、基于知識發現模型、基于動態交通分配模型和基于交通仿真模型等［3］。常用的預測方法有時間序列模型，卡爾曼濾波模型，非參數回歸法，人工神經網絡，支持向量機，灰色模型。時間序列模型建模簡單，在數據充足及交通量周期性平穩變化的情況下，預測精度較高，但在數據有缺失、路段交通量受隨機因素干擾大、不確定性強時，預測誤差較大［4～5］；卡爾曼濾波理論以線性理論為基礎，因此對非線性、不確定性大的短時交通流，其預測誤差較大［6］；近鄰非參數回歸法誤差小，預測精度高，其缺點是要求歷史數據足夠豐富，尋找“近鄰”的工作量較大［7］；神經網絡學習模式需要大量原始數據訓練，數據不足或數據有噪聲都將導致預測結果偏差較大對交通信息的實時采集要求較高［8］。大部分模型普遍存在著“長周期、大區域、低信度”的缺陷，它需要大量的歷史數據，灰色系統理論主要研究“小樣本、貧信息”的不確定系統，在預測中得到了廣泛的應用［9］。

灰色GM（1，1）模型利用累加生成后的新數據建模，其作用是弱化原始數據的隨機性，容易找出數據變換規律，更加容易逼近非線性函數，它適應于變化趨勢較明顯的時間序列，卻對隨機波動大的時間序列則無能為力，而灰色馬爾可夫預測模型先采用GM（1，1）模型擬合交通系統的發展變化趨勢，再對隨機波動大的殘差序列進行馬爾可夫預測，克服了灰色理論的不足［10～11］。本文則采用一種灰色馬爾科夫組合模型，對ofo車流量進行短時預測，該預測只考慮基于道路某一斷面的單點交通流量數據。仿真結果表明，該模型取得比較好的預測結果。

2 灰色理論

灰色理論由鄧聚龍教授于20 世紀80 年代提出，它通過研究少量確切信息的數據樣本，挖掘出未知的有用的信息，以正確認知系統的特性，并以此進行科學預測［12］。作為灰色理論內容之一的灰色模型（Grey Model），它通過對原始數據進行生成處理，來發現和掌握系統發展變動的規律，通過建立相應的微分方程模型，進而對系統的未來狀態做出科學的定量預測［13-16］。

灰色模型GM（1，1）由單變量一階微分方程構成，用于對系統主要因素進行擬合并預測，其主要的步驟為:對原始數據序列x(0)(t)，計算一次累加，生成一個新的序列x(1)(t)，將新序列x(1)(t)的變化趨勢用常微分方程+dx(1)(t)=u 近似描述，之后用離散化和最小二乘法分別求出參數a 和u，獲得灰色預測模型為

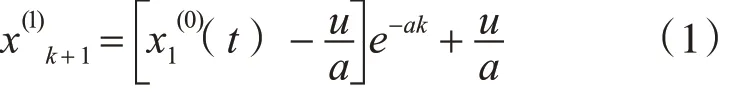
再做累減還原，獲得預測數值:

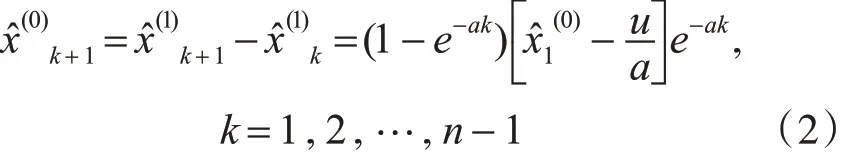
3 馬爾科夫預測

馬爾科夫理論指出:“系統達到每一狀態的概率僅與近期狀態有關，在一定時期后，馬爾科夫過程逐漸趨于穩定狀態而與原始條件無關”的這一特性稱為“無后效性”［17］。馬爾科夫預測方法的特點是:不需要大量的統計資料，只需有限的近期資料即可實現定量預測，而且馬爾科夫預測方法適用于短期預測的基礎上，只要狀態轉移矩陣滾動次數足夠多，同時也適用于長期預測［18］。許多事件發展過程的狀態轉移具有無后效，對于這樣一些事件則可以利用馬爾科夫預測。

3.1 狀態轉移概率

狀態轉移是指客觀事物由一種狀態到另一種狀態的變化。由于狀態轉移是隨機的，因此必須用概率來描述狀態轉移可能性的大小，將這種轉移的可能性用概率描述，就是狀態轉移概率。對于由狀態Ei 轉移到狀態Ej 的概率，稱它為從i 到 j 的轉移概率。公式表達如下:

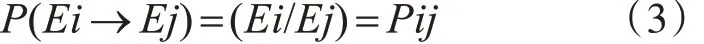
3.2 狀態轉移概率矩陣

假定某一個事件的發展過程有n 個可能的狀態，即 E1,E2,E3,…,En。記 Pij 為狀態 Ej 的狀態轉移概率矩陣，則矩陣為

3.3 終極狀態預測

在馬爾可夫鏈中，己知系統的初始狀態和狀態轉移概率矩陣，就可推斷出系統在任意時刻可能所處的狀態。以k 為時刻，πj(k)為狀態概率（即事件在初始時刻k=0 狀態己知的情況下，經過k 次狀態轉移以后，在第k 個時刻處于狀態Ei 的概率），可以構造如下公式:

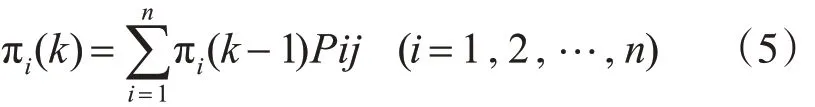
若記行向量 π(k)=[π1(k),π2(k),…,πn(k)]，則由式（5）可以得到計算狀態概率的遞推公式:

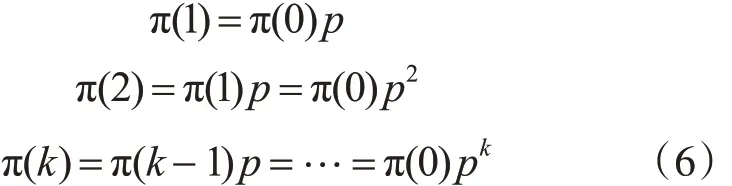
利用式（6）可以計算π(0)在經過k 次轉移后，在k 個時刻處于各種可能狀態的概率，即π(k) ，π(k)則為該事件在k 個時刻的狀態概率預測。經過無窮次狀態轉移后所得到的狀態概率，則稱為終極狀態概率。記終極狀態概率向量為π=[π1,π2,…,πn]，按照極限定義可知:

4 灰色馬爾科夫模型建立

應用灰色一馬爾可夫鏈方法進行預測的基本思路是:對采集到的交通流數據序列x(0)(t)先建立灰色GM（l，1）模型，求出其預測曲線Y（k），再以平滑的預測曲線Y（k）為基準，劃分若干動態的狀態區間，根據落入各狀態區間的點，計算出馬爾可夫轉移概率矩陣預測未來狀態，從而得出預測值區間，取區間中點，最終得到精度較高的預測值［19］。即灰色馬爾科夫模型的建模思路如圖1所示。

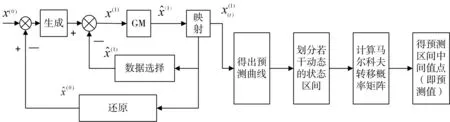
圖1 灰色馬爾科夫系統建模思路

其模型具體建模過程如下［20］:

設原始序列為x(0)=(,,…,)。

1）一次累加生成序列x(1)=(,,…,)，其中:

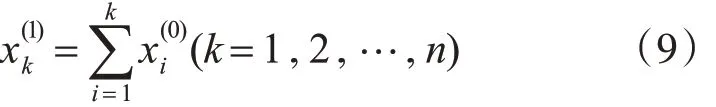
2）確定矩陣B和Yn

設 z（1）是 x（1）的緊鄰均值生成序列，緊鄰均值生成序列 z(1)=(,…,) ，其 中=0.5(+),k=2,3,…,n。

3）用最小二乘法估算一階線性微分方程的參數 a?，u?。

4）白化輸出

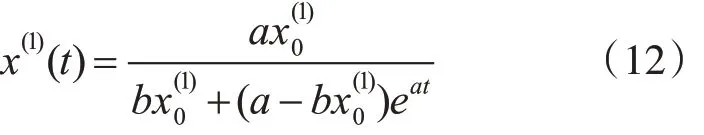
5）累減還原式

5 車流量預測模型實例分析

實驗所用的驗證環境是Windows10 系統下的Matlab2010a。以小寨十字路口路段2017 年9 月1日～9 月8 日共享單車（ofo）需求量的數據實測數據作為數據樣本，其一周內的ofo出行需求變化如表1所示。

表1 白天ofo需求量統計表（單位：輛）

觀測數據表1，以周六數據為例進行灰色馬爾科夫模型的預測。將GM（1，l）模型方法和馬爾科夫鏈優化的GM（1，1）模型所得發展系數和灰作用量分別代入式（13）中，運用Matlab R2010a 軟件編寫代碼來實現2 種預測模型對數據的擬合及預測下一時間段ofo需求量，程序結果顯示如表2。

表2 模型對比

為了更直觀地進行比較，將上面的預測結果和實測值采用Matlab7.0 繪圖工具繪于同一張圖中，如圖2所示。

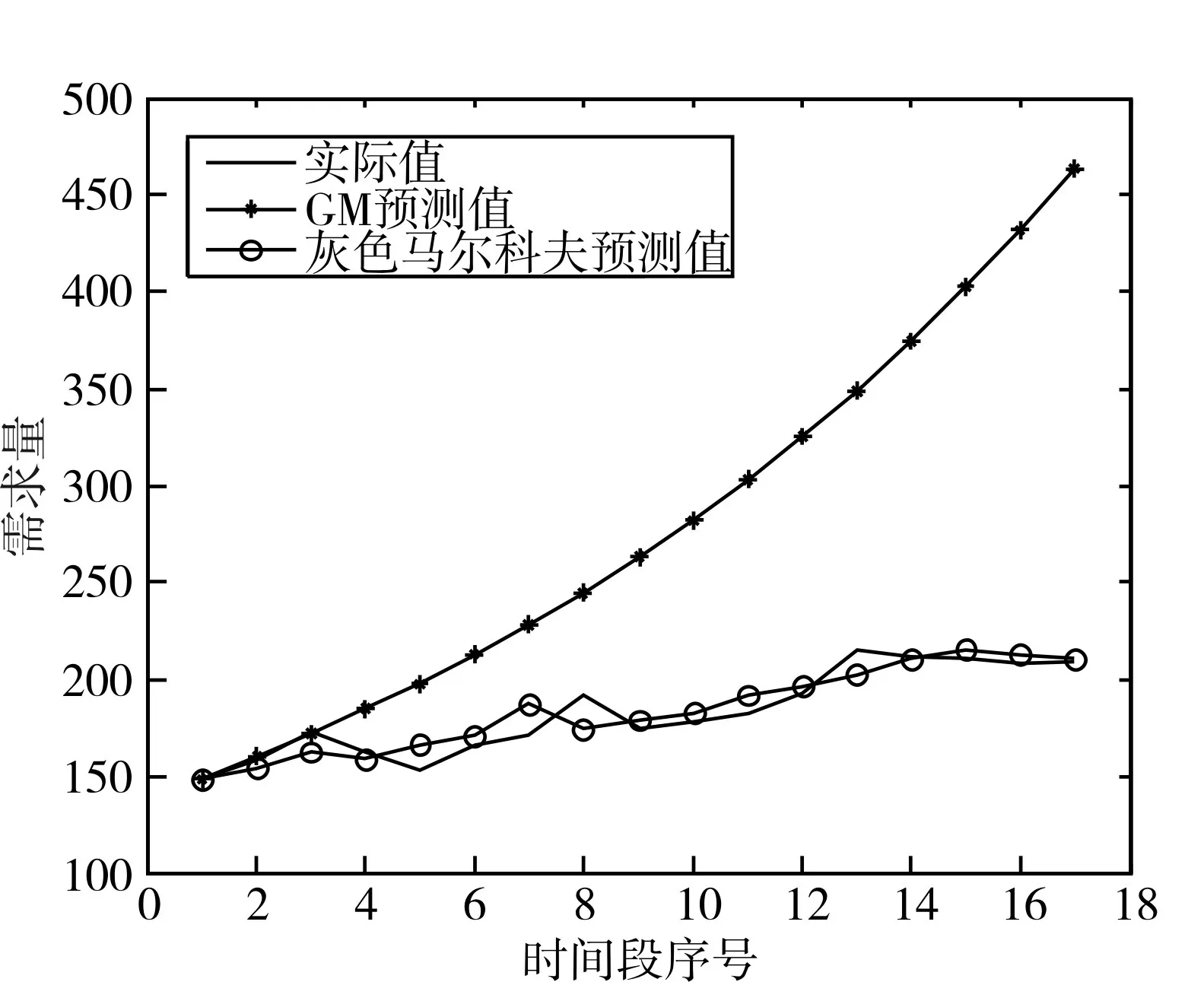
圖2 ofo需求量實際值及2種預測值

參照灰色預測模型的精度檢驗等級表（表3）可知:灰色馬爾科夫模型的平均相對誤差均小于0.05，預測精度為二級（良），即模型精度為二級，可見模型精度較高。GM（1，1）模型適用于具有較強指數規律的序列，只能描述單調的變化過程，而馬爾科夫模型則適用于非常單調的擺動發展序列或具有飽和狀態的S 形序列。而本文所建立的灰色馬爾科夫組合預測模型在一定預測時段內具有良好的預測精度和實用性，即該模型的預測性能更優、更實用。故該模型應用合理，比較適合用于某一時段內ofo需求量的短時預測。

表3 灰色模型精度檢驗等級

6 結語

針對交通系統這種復雜系統，相比于傳統的灰色模型來說，本文采用的灰色馬爾科夫組合預測模型能夠達到在短時間內完成實時預測的要求，預測精度也令人滿意，在一定程度上彌補了GM（1，l）的缺陷，當車流量的變化較大時，采用本方法可較好地改善十字路口的交通狀況。通過理論研究和仿真實驗可知，該灰色馬爾科夫模型預測車流量結果符合要求，其預測有效，可用于需求量波動或飽和階段的預測。