多步強化學習算法的收斂性分析?

楊 瑞

（天津大學數學學院 天津 300072）

1 引言

強化學習（Reinforcement Learning）［1］是解決這樣一個問題的機器學習分支:智能體（Agent）與環境交互，如何自動地學習到最佳策略以使自身獲得最大回報（Rewards）。最近 AlphaGo［2］擊敗了人類頂尖圍棋職業選手，其核心技術之一就是強化學習。強化學習在現代人工智能學中有著舉足輕重的地位，有著廣泛的應用前景［3～4］。

強化學習是一種不告訴Agent如何去正確地決策，而是讓Agent自己去探索環境，在與環境交互的過程獲得知識，不斷優化策略。Agent 與環境交互的過程如下:

1）Agent感知當前環境狀態s；

2）針對當前環境狀態s，Agent根據當前行為策

馬爾科夫決策過程（MDPs）是強化學習的基本框架［5］，可以由四元組＜ S ，A ，P，R＞來表達。 S 是系統的有限狀態集，A 是Agent 的有限動作空間，動作用來控制系統的狀態轉移，:S×A×S'→[0,1]為Agent執行動作a 之后，系統由狀態s轉向s'的概率。:S'×A×S'→1R 表示當 Agent 執行動作a，系統由狀態s 轉到狀態 s'后，系統反饋給略選擇一個動作a；

3）當Agent選擇a，環境由狀態s 轉移到當前狀態 s'，并給出獎賞值（Rewards）R；

4）環境把R反饋給Agent。

如此循環此過程，直至終止狀態，在這個過程中，并沒有告訴Agent 如何采取動作，而是Agent 根據環境的反饋自己發現的。

1.1 馬爾科夫決策過程（MDPs）

Agent的rewards。

策略（policy）定義了Agent 在給定狀態下的行為方式，策略決定了 Agent 的動作。 π:S×A →[0,1]，π（s,a）表示在狀態s 下，執行動作 a 的概率。

在MDP 中，還定義了兩種值函數（Value Function）:狀態值函數Vπ(s)（State Value Function）和狀態-動作值函數 Qπ(s,a)（State-act Value Function）。

Vπ(s)表示 Agent 從狀態 s 開始，根據策略 π 所獲得的期望總回報（Rewards）:

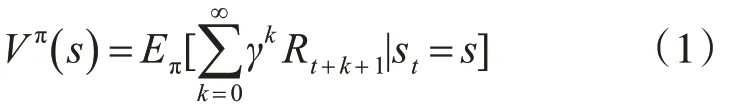
類似地:

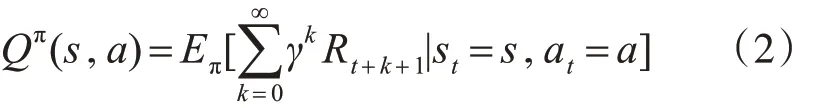
值函數的確定了從一個狀態出發，按照π 所能獲得的期望總回報。

1.2 Bellman 方程

由于MDP 中，狀態轉移滿足Markov 性，1957年，Bellman證明了他的著名方程［6］:

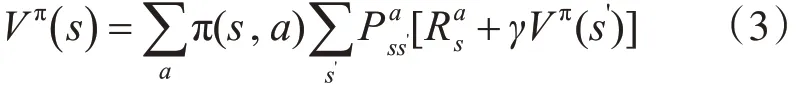
類似地:

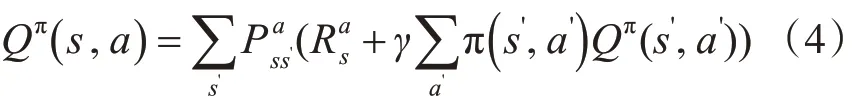
由此可知:系統的狀態轉移矩陣和回報均已知，則易求出Vπ(s)和 Qπ( )s,a強化學習的目標是導出最優策略π*:

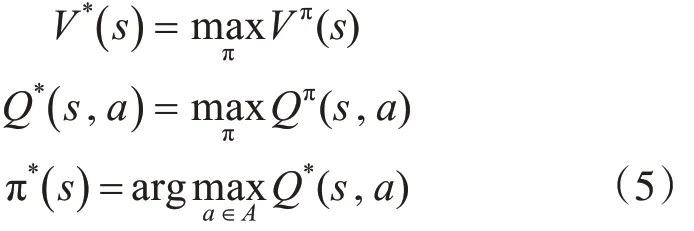
1.3 模型未知的強化學習

MDPs 為強化學習提供了統一的框架，但實際問題中有如下幾個問題:

1）“維數災難”:狀態空間超級巨大，要學習的參數隨著狀態空間的維數指數級爆炸。

2）收斂速度慢:很多強化學習算法的收斂性分析都要依賴“任意狀態都要被無數次訪問到”這樣的前提條件。

3）很多實際問題，我們是無法獲得系統的狀態轉移概率和回報函數的，對這種情況建立模型的算法稱為模型未知的強化學習算法。

最近，有研究人員提出 Q(σ) 算法來估計Qπ(s,a)，并且原文作者通過實驗發現收斂效果很好。本文將對Q(σ)的收斂性給予一個證明。

2 時間差分學習算法框架

時間差分算法（Temporal Difference）是強化學習最核心的一類算法，這項工作首次是在Suton 1988［7］年提出的。這類算法不需要知道系統的狀態轉移矩陣，能夠直接學習。假設Agent 在與環境交互中產生的一個軌道為

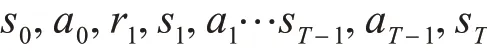
其中sT是終止狀態。

2.1 Sarsa算法

Sarsa［8］算法是根據上述軌跡來迭代 Bellman 方法的解，其名稱是由Agent學習的數據結構而來的，數據是由一個(st,at)轉移到下一個(st+1,at+1)的五元組(st,at,rt+1,st+1,at+1)

Sarsa估值計算公式為

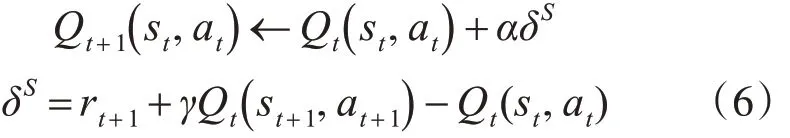
α 為學習率，δ 稱為Sarsa算法的時間差分。

2.2 Expected Sarsa算法

Expected Sarsa［9］:

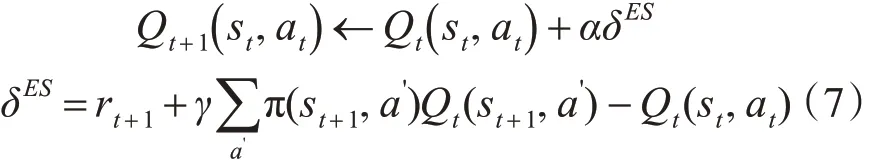
由Sarsa 和Expected Sarsa 的迭代形式可知，Sarsa 是一個全采樣的算法，即在t 時刻，只用rt+1+γQt(st+1,at+1) 來作為目標（target）進行估值。而Expected sarsa 是采用下一狀態st+1的Q 值的期望 :來估值。根據Bellman 等式（4），從直覺上講，Expected Sarsa 的估值要穩定一些［10］。首次證明了 Expected Sarsa 和Sarsa 有相同的 bias，但是 Expected Sarsa 的方差更小一些。

2.3 Q(σ) 算法

Q(σ)［11］算法的設計思想是:引入了參數 σ ，σ是采樣的程度，如果σ=0，表示no-sampling，σ=1表示full-sampling。

單步Q(σ)算法的迭代形式:

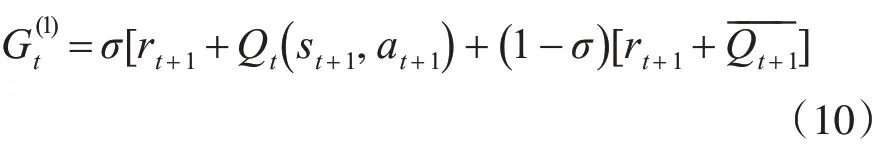
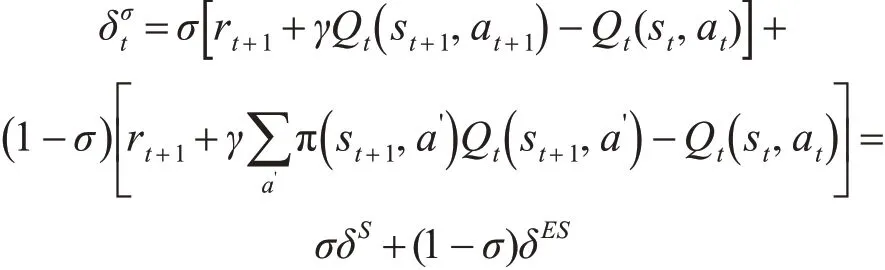
2.4 多步時間差分算法

Sarsa，Expected Sarsa，Q(σ)［12～14］均可以推廣至多步的情況。

2.4.1 多步Sarsa

多步Sarsa值函數的估計公式:

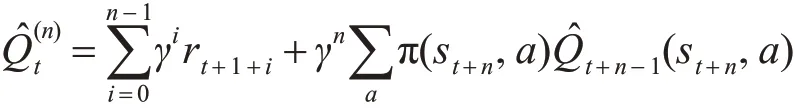
多步Sarsa值函數的更新公式:

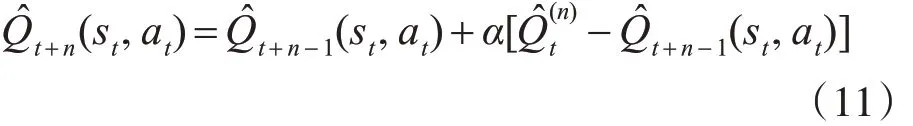
2.4.2 多步Expected Sarsa 算法，也稱多步Tree Backup算法

多步Expected Sarsa也是類似的，但有一些差別。

多步 Expected Sarsa［11］值函數的估計公式:

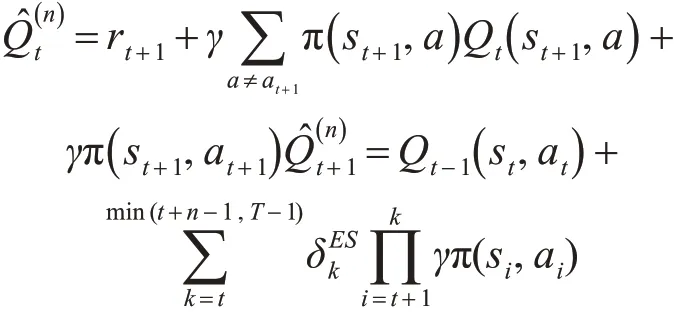
多步Expected Sarsa值函數的更新公式:

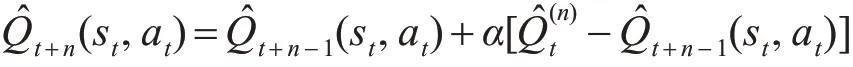
2.4.3 多步 Q(σ)

多步Q(σ)值函數的估計公式:

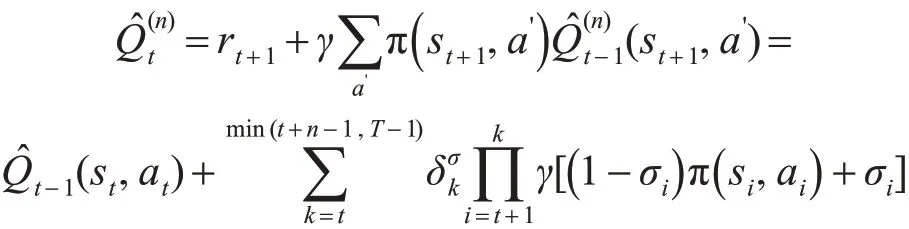
多步Q(σ)值函數的更新公式:

3 Q(σ)算法的收斂性分析

引理 1［15～16］:假設一個隨機過程 (ζt,Δt,Ft) ，ζt,Δt,Ft:X → R 滿足方程:

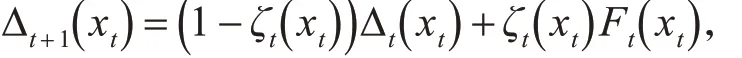
這里 xt?X,t=0,1,2,… 假設 Pt是 σ -fields 的遞增序列，ζ0，Δ0是 P0-measurable，ζt，Δt以及Ft-1是 Pt-measurable，t ≥1。假定以下條件成立:

1）X是有限集；

2）ζt( xt)?[0 ,1],∑tζt( xt)=∞,∑t(ζt( xt))2＜ ∞

w.p.1且?x ≠ xt:ζt( x )=0；

3）∥E{Ft|Pt} ∥≤ κ ∥ Δt∥ +ct，κ ?[ 0,1),ct依概率收斂于0；

4）Var{Ft( xt)|Pt} ≤K(1 +κ ∥ Δt∥ )2,K 是常數。

其中∥?∥表示最大模；則Δt依概率收斂到0。

定理1:在MDP 框架下，對于任意的初始化Q( s,a), ? γ ? ( 0,1) 。

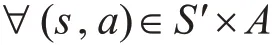
Q的更新按以下方式:

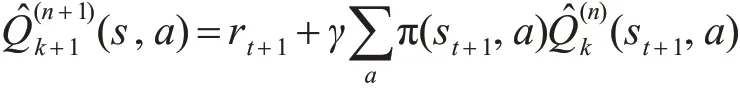
令 Δn=-Qπ(s,a) ，則 有 ||Δn+1||≤γ||Δn||，Δn按最大值范數是壓縮序列，即 Δn依概率收斂于0。

證明:由數學歸納法證明之。

For n=1:

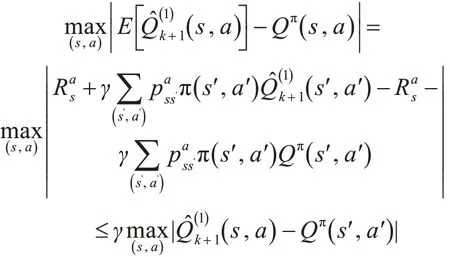
假設對n也成立:

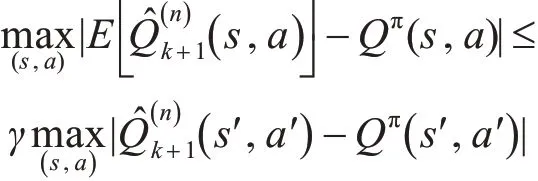
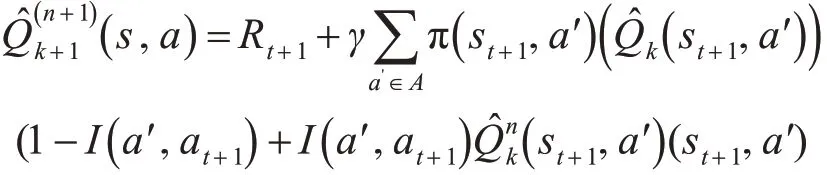
這里I( )a?,at+1是一個指示函數:

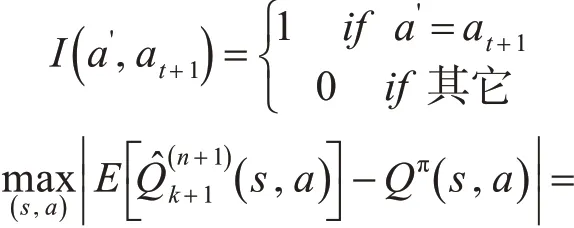
定理2:在MDP 框架下，對于任意的初始Q( s,a),? γ ?( 0,1) 。

事實上，如果定理1中的 π(st+1,a?)滿足:

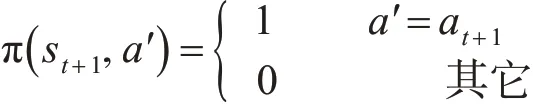
則這就是式（11）所表示的算法，也即是定理1中算法的特殊情況，由定理1 的收斂性可以得到該算法也是收斂的。

定理3:如果Q(σ)算法滿足條件:

1）狀態空間是有限集；

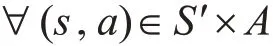
則Q(σ) 迭代產生的Qt(s,a) 依概率收斂于Qπ(s,a)。

定理3的證明:

Q(σ)是定理1 和定理2 所述算法的凸組合，易知 Q(σ) 迭代產生的 Qt(s,a) 依概率收斂于Qπ(s,a)。

4 結語

本文以時間差分學習算法為主線，系統簡要地介紹了強化學習中的幾個重要估值算法，并對最近提出的一個新的時間差分學習算法Q(σ)算法作了理論分析，同時給出了Q(σ)算法的收斂性證明，這在強化學習理論研究中具有重要意義。