一種基于相對信息粒度的屬性約簡算法?

孫 敬

（1.湖北工業大學理學院 武漢 430068）（2.鄭州工業應用技術學院信息工程學院 鄭州 451100）

1 引言

屬性約簡是粗糙集理論的主要研究內容之一，尋找高效屬性約簡算法一直是學者關注的焦點［1～2］。目前，許多學者先后從強化正域［3］、條件熵［4～5］、互信息［6］、區分矩陣［7～8］、粒計算［9～12］、知識粒度［13］、決策重要度［14］、遺傳粒子群［15］、加權濃縮樹［16］等方面提出了自己的方法。但是，這些算法雖然比較了不同屬性集的各方面能力，卻容易忽略知識本身之間的關系。本文將利用粒計算理論，從信息粒庫出發，運用粒之間的運算計算對應的相對信息粒度，據此提出一種基于相對信息粒度的屬性約簡改進算法。

2 相對信息粒度與屬性約簡

2.1 信息粒庫

定義 1［1］設四元組 S=（U，C∪D，V，f）為決策信息系統，其中U 為非空有限的對象集合；C 為條件屬性集，D 為決策屬性集，且C∩D=?，D≠?；V=∪a∈AVa，其中 Va為某屬性 a 的值域；f 為 U×C∪D→V 的信息函數，即對任意的a∈C∪D，x∈U，均有 f（x，a）∈Va。

定義2 設S=（U，C∪D，V，f）為一個決策信息系統，令 a∈C∪D，v∈Va，則稱（a，v）或av為 S 上原子公式。令 m 為 S 上的粒函數，其中 m（av）=｛x | f（x，a）=v，a∈C∪D，x∈U｝，則稱 Gr（a）=（av，m（av））為S上關于屬性a的一個原子粒。

定義3 設S=（U，C∪D，V，f）為一個決策信息系統，設φ、ψ為S 上有限個原子公式利用聯結詞（∧）構成的兩個復合公式，令m（φ）、m（ψ）為滿足公式φ、ψ的對象集合，則稱 Gr（φ）=（φ，m（φ））、Gr（ψ）=（ψ，m（ψ））分別為S 上關于φ、ψ的復合粒，且Gr（φ）∧Gr（ψ）=（φ，m（φ））∧（ψ，m（ψ））=（φ∧ψ，m（φ）∩m（ψ））。

為了更好地從語法和語義方面刻畫屬性與對象之間的關系，借助粒計算理論，下面給出由復合公式和粒函數所確定的信息粒庫的定義。

定義4 設S=（U，C∪D，V，f）為一個決策信息系統，P?C 且 P=｛p1，p2，…，pn｝（n 為 P 的屬性個數），vi∈Vp1×Vp2×…×Vpn，令公式集φp=｛Pvi|Pvi=（p1，v1i）∧（p2，v2i）∧…∧（pn，vni），vi1∈Vp1，vi2∈Vp2，…，vin∈Vpn，i=1，2，3，…｝，令

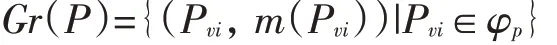
則稱 Gr（P）為 P 對應的 n 階信息粒庫，（Pvi，m（Pvi））為Gr（P）一個n階信息粒。

由定義 4 可知，Gr（P）用公式 Pvi從語法角度闡述了粒的產生規則，m（Pvi）從語義角度闡述了粒的構成對象。

定義5 設S=（U，C∪D，V，f）為一個決策信息系統，P、Q?C，Gr（P）、Gr（Q）為P、Q的信息粒庫，若對 ?（Pvi，m（Pvi））∈Gr（P），均存在一個（Qvi，m（Qvi））∈Gr（Q），使得m（Qvi）?m（Pvi），則稱Gr（Q）比Gr（P）粒化更細，記為Gr（Q）?Gr（P）。

定理1 設S=（U，C∪D，V，f）為一個決策信息系統，若P?Q?C，相應的信息粒庫為Gr（P）、Gr（Q），則有Gr（Q）?Gr（P）。

證明:令 P=｛p1，p2，…，pn｝（n 為 P 的屬性個數），由于 P?Q，則知 Q 比 P 的屬性個數多，令 Q=｛p1，p2，…，pn，pn+1，pn+2，…，pn+m｝（假設pn+1，pn+2，…，pn+m為Q比 P 多的 m 個屬性），對于任意的 m（Qvi）=m（（p1，v1i）∧（p2，v2i）∧…∧（pn，vni）∧（pn+1，vn+1i）∧（pn+1，vn+1i）∧…∧（pn+m，vn+mi））=m（p1，v1i）∩m（p2，v2i）∩…∩m（pn，vni）∩m（pn+1，vn+1i）∩m（pn+1，vn+1i）∩…∩m（pn+m，vn+mi）?m（p1，v1i）∩m（p2，v2i）∩…∩m（pn，vni）=m（（p1，v1i）∧（p2，v2i）∧…∧（pn，vni））=m（Pvi），又知m（Qvi）是任選的，由定義5知Gr（Q）?Gr（P）。

特別地，若 P=Q，則由定理 1 可知 Gr（Q）=Gr（P），此時稱Gr（P）、Gr（Q）粒化相同。

2.2 相對信息粒度

定義6 設S=（U，C∪D，V，f）為一個決策信息系統，P?C，對任意的（Pvi，m（Pvi））∈Gr（P）、（Dvj，m（Dvj））∈Gr（D）（i=1，2，3，…，m，j=1，2，3，…，n，m、n分別為Gr（P）、Gr（D）的公式個數），令

則稱λ（P，D）為 P 關于D 的相對信息粒度，|·|是某個集合的元素個數。

由相對信息粒度定義可知，λ（P，D）反映的是屬性集P 關于D 的粒化論域能力，顯然0 ≤λ（P，D）≤1。λ（P）值越大，說明該屬性集的粒化能力越強，否則，粒化能力就越弱。

定理2 設S=（U，C∪D，V，f）為一個決策信息系統，P?Q?C，則有λ（P，D）≤ λ（Q，D）。

證明:由于P?Q，由定理1 知Gr（Q）?Gr（P），則存在一個（Qvi，m（Qvi））∈Gr（Q），使得m（Qvi）?m（Pvi）（i=1，2，3，…），可知m（Qvi）∩m（Dvj））?m（Pvi）∩m（Dvj））（j=1，2，3，…，n，n為Gr（D）的公式個數），由定義6可知，λ（P，D）≤ λ（Q，D）。

由定理2 可知，屬性集屬性個數越多，其對應的信息粒庫粒化能力越強，屬性集關于D的相對信息粒度值就越大，特別地，若P=Q，由定理2 可知，λ（P，D）= λ（Q，D），顯然，這兩個屬性集的粒化能力相同。

2.3 屬性重要度與屬性約簡

定義7 設S=（U，C∪D，V，f）為一個決策信息系統，對任意屬性a∈C，令

則稱 SIG（｛a｝，C，D）為屬性a 關于D 相對于C的屬性重要度。其中，λ（C，D）、λ（C-｛a｝，D）分別代表C、C-｛a｝關于D的相對信息粒度。

由定義7可知，SIG（｛a｝，C，D）衡量的是刪除屬性a 后引起的C 關于D 的相對信息粒度變化情況，顯然0 ≤ SIG（｛a｝，C，D）≤ 1。當SIG（｛a｝，C，D）=0時，則知λ（C，D）-λ（C-｛a｝，D）=0，即λ（C，D）=λ（C-｛a｝，D），說明刪除屬性a 后C 關于D 的相對信息粒度并未發生變化，屬性a 在C 中是不重要的，或稱冗余的。

性質1 對任意屬性a∈C，它是C 中必要屬性當且僅當SIG（｛a｝，C，D）＞0。

性質 2 核集 COREC（D）=｛a∈C| SIG（｛a｝，C，D）＞0｝。

定義8 設S=（U，C∪D，V，f）為一個決策信息系統，P?C，對任意屬性a∈P，若SIG（｛a｝，C，D）＞0，則稱P是獨立的。

由于以核為起點的啟發式屬性約簡中，需要不斷地往核集中添加屬性，所以下面給出另外一種屬性重要度的定義。

定義9 設S=（U，C∪D，V，f）為一個決策信息系統，P?C，對任意屬性a∈C-P，令

SIG（｛a｝，P∪｛a｝，D）=λ（P∪｛a｝，D）-λ（P，D）

則稱SIG（｛a｝，P∪｛a｝，D）為非P 屬性a 關于D相對于P的屬性重要度。其中，λ（P∪｛a｝，D）、λ（P，D）分別代表P∪｛a｝、P關于D的相對信息粒度。

由定義9可知，SIG（｛a｝，P∪｛a｝，D）衡量的是添加非P屬性a后引起的P關于D的相對信息粒度變化情況，顯然0 ≤ SIG（｛a｝，P∪｛a｝，D）≤ 1，SIG（｛a｝，P∪｛a｝，D）值越大，說明非P屬性a對P越重要。

定理3 設S=（U，C∪D，V，f）為一個決策信息系統，P?C。若P 是獨立的且λ（P，D）=λ（C，D），則稱P為C相對于D的一個約簡。

2.4 基于相對信息粒度的屬性約簡算法

該算法需要先從條件屬性集中選出必要屬性組成核集作為初始約簡集，然后在該集合中不斷添加屬性重要度最大的屬性，循環判斷當前約簡集是否滿足定理3 中約簡的要求，直至算法結束。下面給出本文基于相對信息粒度的屬性約簡算法。

輸入:一個決策信息系統S=（U，C∪D，V，f）。

輸出:決策信息系統的約簡Red（S）。

步驟1:計算λ（C，D），令Red（S）=COREC（D）；

步驟2:判斷λ（Red（S），D）=λ（C，D）是否成立，若成立，則跳轉到步驟4，否則跳轉到步驟3；

步驟3:對于任意a∈C-Red（S），計算其屬性重要度 SIG（｛a｝，Red（S）∪｛a｝，D），令 Red（S）=Red（S）∪｛a｝，其中屬性a為所有C-Red（S）中屬性重要度最大的屬性（若多個屬性值最大，任選一個加入Red（S）），執行步驟2；

步驟4:算法結束，輸出約簡Red（S）。

3 實例分析

利用文獻［1］中的一個決策信息系統（表1），下面將驗證本文算法的有效性。其中，U=｛x1，x2，x3，x4，x5，x6｝，C=｛a，b，c｝，D=｛d｝，利用文獻［1］得到的約簡為｛ab｝或｛ac｝。

結合上述決策信息系統，下面給出本文屬性約簡算法的具體執行過程，以此來驗證本算法的有效性。

首 先 ，計 算 λ（C，D）。 Gr（C）∩Gr（D）=｛（（a2b2c0d1），｛x1｝），（a1b2c0d0），｛x2｝），（a1b2c0d1），｛x3｝），（（a0b0c0d0），｛x4｝），（（a1b0c1d0），｛x5｝），（a2b0c1d1），｛x6｝）｝，所以 m（C）∩m（D））=｛｛x1｝，｛x2｝，｛x3｝，｛x4｝，｛x5｝，｛x6｝｝，λ（C，D）=1-1/6=5/6。對任意的 a∈C，逐一計算 SIG（｛a｝，C，D），可得 SIG（｛a｝，C，D）=5/6-7/9=1/15，SIG（｛b｝，C，D）=SIG（｛c｝，C，D）=5/6-5/6=0，COREC（D）=｛a｝，令Red（S）=COREC（D）=｛a｝。

表1 決策信息系統S

判斷當前約簡集是否滿足條件λ（Red（S），D）=λ（C，D）。由于λ（Red（S），D）= λ（｛a｝，D）=13/18≠5/6=λ（C，D），所以對任意的b∈C-Red（S），計算SIG（｛a｝，Red（S）∪｛a｝，D），可得 SIG（｛b｝，｛a｝∪｛b｝，D）=SIG（｛c｝，｛a｝∪｛c｝，D）=5/6-13/18=1/9＞0，按步驟3任選屬性b加入約簡集中，即Red（S）=｛ac｝。

對于Red（S）=｛ac｝，判斷λ（Red（S），D）=λ（C，D）是否成立。由于λ（｛ac｝，D）=λ（C，D）=5/6，條件成立，轉向步驟4，算法結束，輸出約簡集Red（S）=｛ac｝。

同樣，可驗證｛ab｝也是該決策信息系統的約簡，這與文獻得到的約簡集是一致的，說明該算法是有效的。

4 結語

本文依托粒計算理論，從原子粒和復合粒出發，介紹了信息粒庫的概念，據此給出了相對信息粒度來度量某屬性集關于決策屬性集的相對粒化能力，并提出了一種基于相對信息粒度的屬性約簡算法，結合實例分析為決策信息系統屬性約簡提供了一種新的研究方法。