橋梁健康監測中車輛荷載應變的實時分離

曹少杰

（山西交通控股集團有限公司 運城南高速公路分公司，山西 運城 044000）

0 引言

在橋梁健康監測中，應變反映結構的局部受力。應變監測在結構健康監測中具有十分重要的地位，幾乎國內外的所有橋梁健康監測系統中，都布設了大量的應變傳感器。

大量的運營期監測數據表明，監測應變數據一般具有由長期趨勢變化、周期性變化及隨機變化等部分效應疊加的。長期趨勢變化主要是由混凝土收縮徐變引起，周期性變化主要是由溫度變化引起，而隨機變化則是由車輛荷載及其他偶然荷載引起。長期趨勢及周期性變化是緩慢連續的，而隨機荷載變化則是突變和離散的。隨機荷載中風荷載及偶然荷載產生的應變較少可以忽略，因此假定隨機荷載主要是由車輛荷載引起的。

在橋梁健康監測中，如何實時并準確獲得車輛荷載產生的應變效應，并以此進行安全預警，對于掌握結構受力及保障大橋安全具有非常重要的意義。文獻[1]采用二次滑動平均法進行應變趨勢項解耦，從而獲得車輛荷載產生應變，但未明確該方法是實時在線處理還是定期進行離線處理[1]。文獻[2]采用改進的移動平均法進行應變測試數據處理，將實測數據分為趨勢項和離散項兩部分，從而提取出車輛荷載產生應變[2]。但該方法適用于離線分析，不適合在線分析。文獻[3]采用小波分析的方法將車輛荷載分離[3]，主要研究應變監測中的溫度效應，對車輛荷載效應較少涉及。

本文通過對多種數據處理方法的對比，系統總結各種方法的優缺點，從而尋找出一種適合于在線分析的數據處理方法，提高了數據的實時性和準確性。

1 改進的移動平均法

移動平均法是用一組最近的實際數據值來預測未來一期或幾期數據的一種常用方法。其計算方法是：

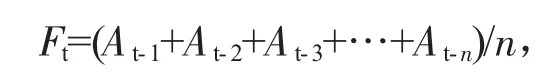
式中：Ft為對下一期的預測值；n 為移動平均的時期個數；At-1、At-2、At-n為前期實際值。

移動平均方法能夠用于狀態預測。當數據不會迅速或快速增長，移動平均法可以有效地消除數據的隨機誤差。平滑處理方法將車輛荷載產生的應變看做噪聲，是隨機出現的（圍繞著總體趨勢上下擺動），均值為0（表明噪聲可能有正有負）。而實際采集的數據卻明顯與此不同，車輛荷載產生的應變基本上只出現在一個方向。因此，采用傳統的平滑處理方法會帶來較大的誤差，必須對此進行改進。圖1 為某橋健康監測中應變實測曲線圖，從圖中明顯看出車輛荷載產生應變大多數為正應變。

文獻[2]便是在上述移動平均的基礎上進行了改進。根據相對變化量分辨當前數值是否包含車輛荷載影響，選擇沒有車輛荷載影響的數據采用移動平均法進行平滑分析，從而得出測試數據的總體趨勢線。具體方法是：首先確定分離汽車荷載應變的閾值。其次確定初始值，選擇數據前端n 個實測值tn，將其平均值作為數據起算的初始值F0。然后以該初始值作為第n+1 階段的預測值，若｜tn+1-F0｜設定閾值，則將F0與tn+1的平均值作為n+2 階段的預測值，否則仍以上階段的預測值作為n+2 的預測值，將tn+1- F0作為車輛荷載的影響值。如此反復循環，當循環次數達到移動平均所需的周期k 時，則以k個數據的平均值即Fn+k=(Fn+k-1+Fn+k-2…+Fn+k)/n 作為下一狀態（n+k+1）的預測值，并按照前述方法與實測值進行比較，分離出汽車荷載影響，如此反復循環直至數據結束。采用上述分析方法對能夠有效地分離出車輛荷載產生的應變[2]，如圖2、圖3 所示。

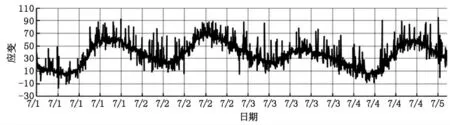
圖1 應變實測曲線圖

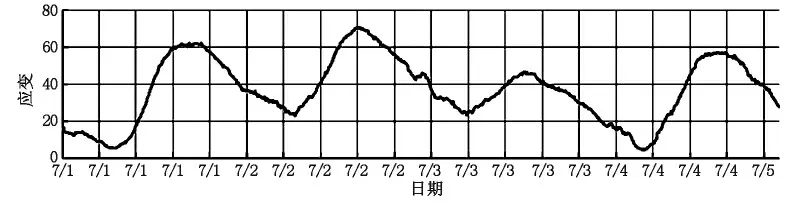
圖2 平滑處理后的應變趨勢線曲線圖

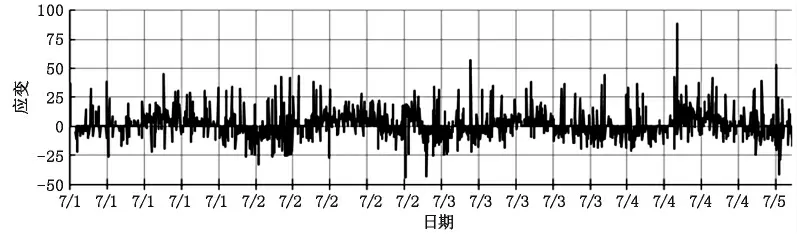
圖3 平滑處理后的應變離散線曲線圖

然而，在實際應用過程中，發現移動平均法具有如下缺點，無法滿足橋梁健康監測的需要：

a）該方法是在收集一個月實測數據基礎上進行，具有一定的滯后性，不能及時地識別出車輛荷載，因此也無法進行結構狀態實時判斷和預警。也就是說采用移動平均法進行車輛荷載識別需要一定長度的數據進行識別，當為實時在線數據時，由于移動平均法的滯后特性，將會造成最新識別的車輛荷載誤差較大，因此無法適應在線監測。

b）移動平均法是將所有數據進行平均得到的，實際上由于車輛荷載的隨機性，需要對移動平均法進行相應的改進，而改進后的算法由于需要進行反復搜索平滑區段，造成計算速度慢、效率低、且計算機資源占用較大。

2 卡爾曼濾波法

卡爾曼濾波器是線性系統狀態方程，是用于通過系統輸入和輸出觀測數據系統狀態的最優估計算法。由于觀測數據包括系統中的噪聲和干擾的影響，最佳估計也可以被認為是上述的濾波處理。

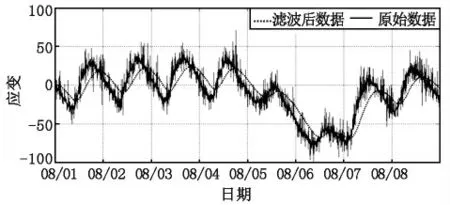
圖4 采用卡爾曼濾波法進行數據處理

同樣采用卡爾曼濾波法對監測數據進行處理，將車輛荷載產生的應變也視同噪聲，從而獲得實測數據的總體趨勢，將實測原始數據減去總體趨勢項，在考慮到應變測試誤差的基礎上，從而獲得車輛荷載產生應變。如圖4 所示。

從圖4 可以看出，采用卡爾曼濾波法進行數據分析，存在滯后性，得出的應變趨勢線與實測應變存在一定的相位差，無法滿足項目的實際應用。

3 小波分析

小波變換是采用一個函數的平移伸縮作為基底進行頻譜研究。將測試信號的每一個瞬間分量映射到時頻平面上的相應位置，該位置正好對應于分量的頻率和發生時間，從而將測試信號分解為不同頻率及不同時刻的相應測試結果。其中的高頻信息能夠反映信號的突變，而低頻信息則反映著信號的近似形狀[4]。

對測試數據進行多層小波分解，根據數據測試結果選擇合適的小波基及相應的分解尺度，經多次試算進行4～6 層分解是較為合理的。結果如圖5。

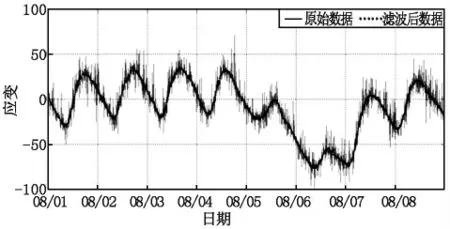
圖5 采用小波分析法進行數據處理

圖5 中的實線為實測數據，虛線為小波分析后得出的實測曲線中的低頻信號也就是近似值，通過選取合理小波基函數及相應的分析尺度，便可將實測曲線中的趨勢線與離散線區分出來，從圖中可以看出，采用小波分析后的數據與原始數據具有較好的吻合度。

4 健康監測中車輛荷載應變的實時分離

通過上述各種數據處理方法的對比，小波分析在數據處理方面具有一定的優點，但由于需要對一段連續數據進行分析處理，實際監測數據是不斷更新的，因此需要分段進行小波分析。

采用上述數據，分段進行小波分析，并與未分段的小波分析結果進行對比，二者在分段的前端與末端均存在一定的截斷誤差。針對這種情況，采取分段小波分析結合多次修正進行數據處理，每次分段長度取較大值，而時間間隔取較小值，通過多次修正，最終消除截斷誤差。

根據上述研究成果，在監測系統軟件編寫過程中，將小波分析編寫入采集軟件中，實現分段和定時的小波分析，從而確定出應變趨勢曲線。基本反映了應變的總體變化規律，得出的車輛荷載應變也反映了大橋實際的受力狀況。

5 結語

通過對不同的數據處理方法進行研究，采用分段小波分析進行車輛荷載應變的實時分離是能夠滿足工程應用的，基本反映了大橋的實際受力狀況，通過對車輛荷載產生應變進行統計分析，確定相應的預警閾值，從而可實時判斷結構的受力狀況，保障大橋的受力安全。