基于無積分節點間斷有限元的二維水沙模型:(2)泥沙運動與地形演變
韓 露,張慶河,李龍翔,冉國全,李文俊
(天津大學 水利工程仿真與國家重點實驗室,天津 300072)
泥沙運動對于河口海岸演變、航道淤積以及河口治理等問題有著重要的影響,一直是河口海岸地形演變過程的研究重點。近年來,隨著計算機技術的發展,數值模型越來越成為研究泥沙運動的重要手段。目前,二維水沙模型在解決工程泥沙問題中的應用已十分普及。過去幾十年來,有限差分法、有限元法和有限體積法等經典數值方法均在二維水沙模型中得到大量應用。有限差分法建立在經典數學逼近理論的基礎上,簡潔直觀,但差分法一般不易保證計算的守恒性[1-2];有限單元法計算精度相對較高,但不適于計算間斷問題[3-4];有限體積法在實際應用中,可以保證不同網格下的積分守恒,能夠計算間斷問題,但很難在一般非規則網格上取得高精度[5-6]。與上述三種經典方法相比,間斷有限元法(Discontinuous Galerkin Method)因在數值精度、間斷捕捉能力、網格自適應特性、緊致性、高度可并行性以及適用于非結構化網格等方面的優勢,近年來逐漸開始在二維水沙模型的研究中得到應用[7]。
Gourgue[8]較早采用間斷有限元方法建立了二維水沙數值模型,并應用于Scheldt河口泥沙運動研究。石寶海和陳煥貞[9]基于迎風間斷有限元方法建立了平面二維水沙輸運模型,泥沙運動采用挾沙力模型描述,并給出了一個理想算例結果。趙張益和張慶河[10](2014)采用間斷有限元法建立了具有二階精度的非結構化網格二維懸沙數值模型,模型能夠有效限制間斷處的數值振蕩,保證穩定性,但是該模型未考慮推移質輸沙和地形演變的影響。
上述研究表明,間斷有限元可以用于二維水沙運動的模擬,然而,這些模型中包含的正交項是基于全階積分的,這需要大量的計算資源[11]。為了減少這種計算量,Atkins和Shu[12]提出了無積分節點間斷有限元格式,該格式避免了離散方程時的積分過程,能夠有效減少計算時間以及存儲空間,并可以保持間斷有限元固有的緊致性和穩健性,具有良好的應用前景,但是該方法要求單元的雅克比系數為常數,不能適用于任意四邊形網格。李龍翔和張慶河[13]在此基礎上建立了適用于任意四邊形網格的無積分節點間斷有限元模型,用矩陣運算進行數值積分,有效地減小了四邊形網格上模型計算所需的存儲空間與計算量。李文俊等[14]在二維淺水方程中加入了科氏力、風應力、底摩阻項,基于無積分節點間斷有限元建立了充分反映各種實際條件影響的二維水動力模型。
本文將在李文俊等[14]二維水動力模型基礎上,進一步基于無積分節點間斷有限元建立二維泥沙運動與地形演變模型,同時,本模型采用了李龍翔和張慶河[15]提出的采用權重重構方法的節點型斜率限制器來消除間斷處產生的振蕩,為二維高效高精度無積分節點間斷有限元二維水沙模型的建立奠定基礎。
1 二維泥沙運動及地形演變數學模型
1.1 水動力方程
模型的水動力計算采用二維淺水方程作為控制方程,該方程是由三維N-S方程在采用靜壓假定,忽略粘性以及垂向加速度的情況下,沿水深積分得到的
(1)
式中:U= [h,hu,hv]T,F(U)=[E(U),G(U)]T,S(U)分別代表守恒變量、通量項以及源項,表達式寫為
(2)
(3)
式中:h為總水深;g為重力加速度;u和v分別為x方向和y方向的垂線平均流速;z為底部高程;η=h+z為水位;Sfx和Sfy分別為x方向和y方向底摩阻項,可表示為
Sfx=n2u(u2+v2)1/2h-4/3,Sfy=n2v(u2+v2)1/2h-4/3
(4)
式中:n為曼寧系數。
1.2 泥沙運動控制方程
泥沙運動暫時只考慮非粘性泥沙,按照其運動型式可分為推移質和懸移質,下面分別給出描述泥沙運動的推移質運動公式和懸移質運動控制方程。
1.2.1 推移質運動控制方程
推移質運動控制方程一般用經驗公式表示,本文采用van Rijn[16](2007)公式
qbx=0.015uh(d50/h)1.2Me1.5qby=0.015vh(d50/h)1.2Me1.5
(5)
式中:qbx和qby分別為x和y方向的推移質泥沙濃度;d50為泥沙中值粒徑;Me表達式為
Me=max(0,|uc|-ucr,c)/[(s-1)gd50]0.5
(6)
式中:uc為水平方向的合速度;s為泥沙密度與液體密度的比值;ucr,c為泥沙運動的臨界流速,表達式為
(7)
式中:d90表示一個樣品的累計粒度分布數達到90%時所對應的粒徑。
1.2.2 懸移質運動控制方程
懸移質泥沙運動控制方程采用沿水深平均的二維對流擴散方程
(8)
式中:c為沿垂向平均后的泥沙濃度;εx和εy為泥沙的水平擴散系數;Fs為源項。
源項可以采用挾沙力公式或參考濃度法描述,本文采用參考濃度法[17]進行計算
Fs=P-D=(ca-c0)wf
(9)
式中:P為泥沙起懸通量;D為泥沙沉積通量;wf為泥沙沉速。ca和c0是定義在參考高度處a的濃度,ca與底床切應力有關,表示懸沙平衡時參考高度處的泥沙濃度,c0與對流擴散方程的垂向平均濃度有關,表示在水深平均濃度對應于參考高速度處的濃度。當ca>c0時,泥沙起懸,當ca (10) 式中:τs,max為最大底部應力;τcr為泥沙顆粒臨界啟動切應力;βd為垂向濃度分布轉換系數,由下式計算 (11) (12) 式中:κ為馮卡門系數,一般取0.4;u*c為底摩阻流速。 推移質和懸移質的泥沙濃度會引起底床的沖刷和淤積變形,底床的地形演變可通過以下方程描述 (13) 式中:p為泥沙的孔隙率。 水動力模型中淺水方程的數值離散過程已在文獻[14]中給出,下面重點給出懸沙輸移對流擴散方程與地形演變方程的離散過程。 式(8)中含有2階偏導項,為將方程改為一階偏導方程,引入輔助變量[19] Q=εhc (14) 此時二維對流擴散方程可改寫為 (15) 為方便離散,將(13)、(15)式寫為 (16) 式中:W為守恒通量,W=[hc,z]T,P(W)=[K(W),L(W)]和R(W)分別代表守恒變量通量項以及源項,表達式寫為 (17) (18) 與水動力模型的離散過程類似[14],將求解域劃分為Ne個非重疊單元Ωe[6],定義Ωe上至多為p階的多項式空間Vp(Ωe),取Lagrange插值函數作為試驗函數φVP(Ωe),將試驗函數乘以式 (14)和(16),并在單元Ωe上積分,可得 (19) (20) 對式(18)進行分部積分,得到離散方程 (21) 式中:n為本單元邊界處的外法向向量,由于相鄰單元在交界面兩側的值不同,為保證兩側單元流入與流出的通量守恒,引入數值通量(hc)*,采用中心通量計算[20] (hc)*=0.5(hc-+hc+) (22) (23) 對控制方程離散后的強形式進行進一步離散,得到如下的半離散格式 (24) 式中:uh為未知變量的矢量。 式(28)的時間遞進可以采取歐拉法、龍格庫塔法等求解。為了盡可能減小時間離散誤差,本文采用顯式四階龍格庫塔方法[22]用于半離散方程的時間遞進。 (25) 式中:系數ai,bi,ci的取值參照文獻[22]。 下面分別利用前人進行的泥沙懸揚、沙波演變和潰壩波沖淤水槽試驗對建立的泥沙運動與地形演變模型進行驗證。最后,還將模型應用于海南省紅塘灣附近海域的模擬,與現場實測懸沙資料進行比較。 該算例為van Rijn[23]在圖1所示的水槽中所做的泥沙懸揚實驗。水槽中分為定床段和鋪沙段,鋪沙段長30 m、寬0.5 m、高0.7 m。水深為0.25 m,平均流速0.67 m/s,底床泥沙中值粒徑為0.23 mm。Lin 和 Falconer[24]曾用數學模型對此實驗進行了模擬,本文模擬時的相關系數均參考文獻[24]進行取值。懸沙沉降速度取為0.022 m/s,水平擴散系數取為0.002 m2/s。 圖2為模型模擬結果與實測垂向平均含沙量結果的對比,結果表明,本文模型的數值解與實測值基本接近,泥沙輸移趨勢相同,模型可以有效地模擬泥沙懸揚以及輸移過程。 圖1 實驗布置圖Fig.1 Layout of experiment圖2 垂向平均含沙量模擬值與實測值對比Fig.2 Comparison of simulated and measured vertical average sediment concentration 該算例在不考慮懸移質泥沙條件下模擬沙波地形演變過程[25],用以檢驗模型模擬地形演變數值模型的合理性。初始沙波為正弦形,源項取為0,推移質表達式取為 (26) 式中:a和b為常數;u=(ux,0)為沿水深平均的流速;D=(Dx,0)為流量;Δy=1.2 m為寬度;a=0.001 s2·m-1;b=3;Dx=1 m3·s-1,初始地形的函數可參考一維算例[26]。 圖3為y=0.75 m處剖面在t=500 s時模型模擬結果與文獻[25]給出的解析解的對比,結果表明,本文模型的模擬值與解析解吻合較好,模型可以精確地模擬地形演變過程。圖4為本文模型計算結果與文獻[25]基于有限體積方法給出考慮人工擴散項的計算結果與解析解誤差的對比圖,可以看到,本文的模擬值誤差更小,精度更高。 圖3 沙波演變模型模擬值與解析解的對比Fig.3 Comparisons of simulated values and analytical solutions圖4 間斷有限元與文獻[25]考慮擴散項有限體積法誤差對比Fig.4 Error comparisons of discontinuous Galerkin method and finite volume method with additional diffusion in reference[25] 圖5 潰壩算例的實驗布置圖 (m)Fig.5 Layout of dam break experiment 該算例出自Leal的潰壩實驗[27],實驗在一個長19.2 m、寬0.5 m、高0.7 m的水槽中進行,圖5為初始時實驗布置的示意圖,水槽分為左右兩端,左段在固定床面之上鋪沙高度為0.19 m,水深0.4 m,右側鋪沙高度為0.071 m,水深0.075 m。泥沙中值粒徑為1.22 mm,泥沙沉速為9.92 cm/s。 圖6和圖7分別顯示了t=1 s和t=4 s時模型模擬與實驗測量水位值和地形值的比較情況。雖然水位、地形模擬值與實測值在局部有一定差異,二者變化趨勢總體上吻合較好,可以認為模型能夠合理模擬復雜水流及其引起的泥沙沖淤導致的快速地形演變問題。 圖6 t=1 s時模擬值與實測值的對比Fig.6 Comparisons of simulated and measured values at t=1 s圖7 t=4 s時模擬值與實測值的對比Fig.7 Comparisons of simulated and measured values at t=4 s 圖8 三亞紅塘灣泥沙測站布置圖Fig.8 Layout of sediment station in Hongtang Bay of Sanya 為了進一步考察二維水沙模型模擬實際海域水沙運動的合理性,本節選取三亞市紅塘灣附近海域,模擬了2016年4月26日~27日一個完整大潮期間的泥沙運動。本算例計算域與文獻[9]相同,潮流模擬結果與實測資料的比較見文獻[14],這里主要給出懸沙運動模擬結果。根據現場實測資料分析,懸沙中值粒徑取為0.3 mm,懸沙沉降速度取為0.035 m/s。 現場全潮水文觀測包含潮流與懸沙測量,這里選取S1~S6共六個測站的懸浮泥沙資料與模擬結果進行比較。泥沙測站位置如圖8所示。模擬結果與實測結果比較見圖9。由圖可知,模型模擬的泥沙運動與實際觀測情況吻合良好。可以認為,本文建立的水沙模型能夠合理模擬比較復雜的現場實際情況。 圖9 2016年4月26日~27日大潮期懸沙濃度模擬值與實測值對比Fig.9 Comparison of simulated and measured suspended sediment concentration during high tide period (2016-04-26~27) 基于無積分節點間斷有限元方法建立了泥沙輸移二維數學模型,懸沙運動通過對流擴散方程進行離散求解,方程的源項采用參考濃度法,推移質輸沙采用經驗公式進行計算,地形演變過程則通過推移質和懸移質輸沙控制的床面變形方程進行求解。建立的泥沙輸移與地形演變數值模型獲得了已有水槽沖刷試驗、沙波演變解析解和潰壩動床實驗的驗證。模型還應用于三亞紅塘灣大潮過程懸沙運動的模擬,模擬結果與全潮水文觀測多點含沙量過程吻合較好。模型驗證和應用結果表明,基于無積分節點間斷有限元建立的水沙模型可以合理模擬泥沙運動及其導致的地形演變問題。 為了更全面描述河口海岸泥沙二維運動問題,模型將進一步考慮波流共同作用下二維水動力及泥沙運動。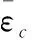
1.3 地形演變方程
2 控制方程數值離散
2.1 對流擴散方程與地形演變方程的離散
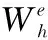
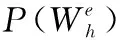
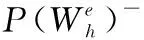
2.2 時間遞進
3 模型驗證與應用
3.1 泥沙懸揚算例
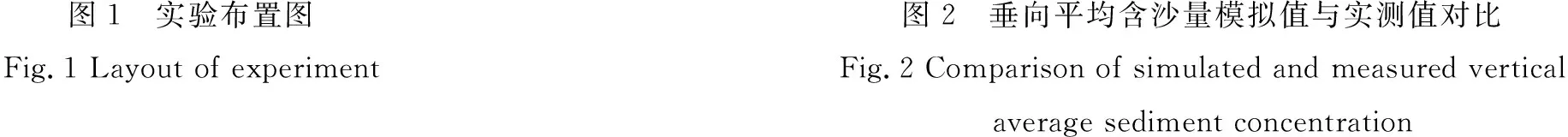
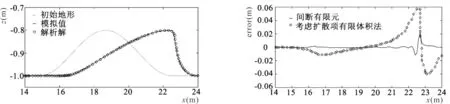
3.2 沙波演變算例

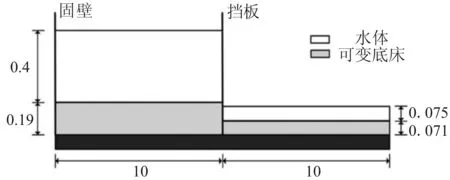
3.3 潰壩動床算例


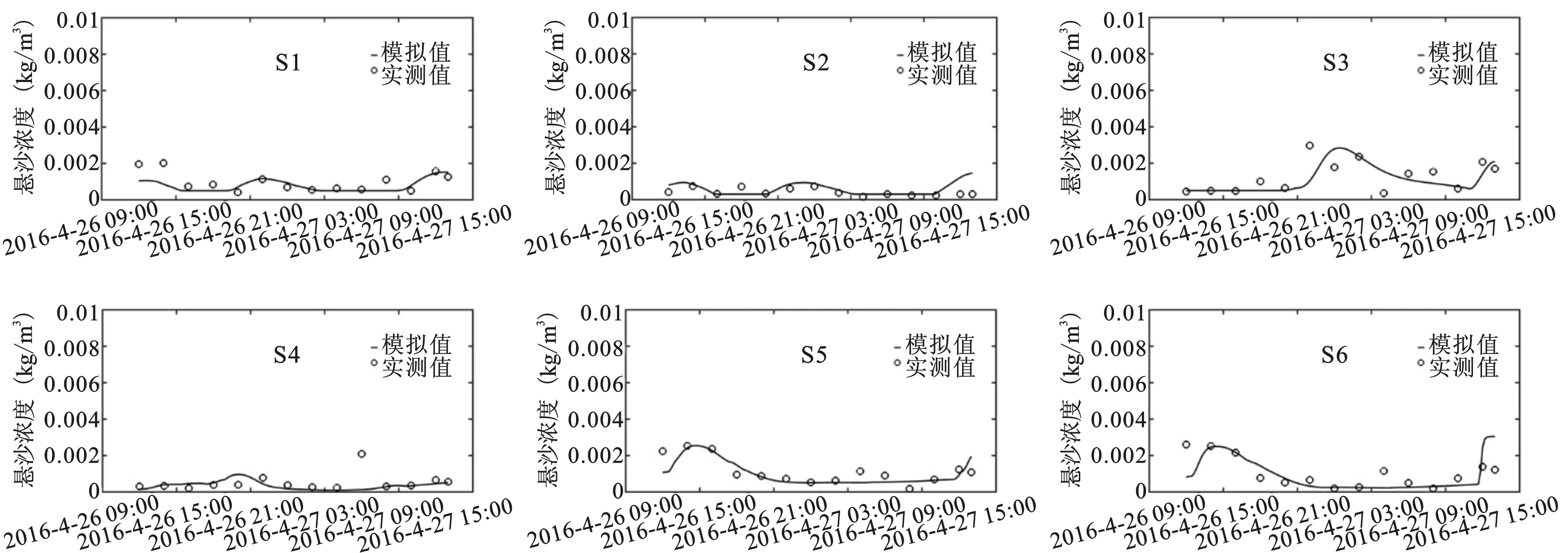
3.4 模型在三亞紅塘灣泥沙運動模擬中的應用
4 結論

