勢函數特征參數調節隨機共振及動車軸承故障檢測研究

劉進軍, 冷永剛, 張雨陽, 譚 丹, 范勝波

(1.天津大學 機械工程學院，天津 300350;2.天津城建大學 控制與機械工程學院，天津 300384)

近年來我國高速列車發展迅速，根據2016年新修訂的《中長期鐵路網規劃》，到2025年全國高速鐵路通車里程將達到3萬公里。在高速鐵路對促進社會經濟發展、保障和改善民生等發揮重要作用的同時，高速列車運行的安全問題也越來越受到高度的關注。高速列車轉向架的軸承是車組的關鍵部件之一，其運行工況較為惡劣，因此需要對其進行實時監測與故障檢測診斷，以保障列車安全可靠的運行。目前針對列車滾動軸承故障的檢測主要有軸溫監測、油液分析、聲學及振動信號檢測分析等方法。隨著信號采集設備以及信號處理方法的發展，振動信號采集分析法逐步成為故障檢測與診斷的主要方法。

為了能有效提取與識別軸承等機械故障的特征信號，一些方法如小波變換[1-2]、經驗模式分解EMD(Empirical Mode Decomposition)[3]、數學形態學[4]和非線性系統理論[5]等得到了廣泛深入的研究與應用。其中非線性系統(如雙穩系統、Duffing 振子系統等)中存在著非同尋常的隨機共振現象而頗受關注。該現象因具有利用噪聲增強微弱信號的新穎特點，而逐步成為機械故障診斷中的研究熱點。為了能夠將隨機共振方法應用于諸如早期微弱故障信號的檢測，人們克服了隨機共振理論小參數條件以及低采樣頻比的限制，研究發展出了變尺度[6]、調制解調[7]、參數歸一化[8-9]、多尺度噪聲[10-11]、頻域信息交換[12]等多種隨機共振方法，這些方法在已工程應用中得到了一定的驗證應用。

上述研究方法都涉及到非線性系統參數的調節，而系統參數的調節都會引起勢函數特征——勢壘高度和勢阱間距的同時變化，這無疑給清晰觀察勢函數某一特征如何影響隨機共振帶來了困難。如果有一種方法能夠單獨反映勢函數的勢壘高度或勢阱間距的變化，那么將有助于直觀理解勢函數特征對隨機共振的影響，并可進一步將隨機共振有效應用于實際中。文獻[13]提出利用正弦函數構造勢阱，通過調整波形的幅值和周期，實現勢阱勢壘高度和勢阱間距單獨調節。但是正弦勢阱兩側的側壁高度與勢壘高度相同，從物理意義上理解，粒子可能會越出構造的勢阱，落入兩側其他勢阱中。因此該方法雖然能夠將勢壘高度和勢阱間距分離，但非線性系統勢函數類型被徹底改變，相應的系統隨機共振特性也被改變，這并不利于實際應用。

為了能夠單獨觀察理解系統勢函數的勢壘高度或勢阱間距與系統隨機共振的關系，在保證勢函數類型不變的前提下，本文以非線性雙穩系統為研究對象，提出基于勢函數特征參數調節的隨機共振方法。通過變量代換對勢函數特征參數(Potential Function Characteristic Parameters,PFCPs)——勢壘高度參數和勢阱間距參數進行解耦，來掌握勢壘高度和勢阱間距的調節對勢函數的影響。此外，為了解決低采樣頻率比隨機共振難以實現問題，本文將勢函數特征參數調節方法與頻域信息交換方法(Frequency Information Exchange Method,FIE)相結合，給出頻域信息交換和勢函數特征參數調節的隨機共振方法，并應用于高速列車滾動軸承故障的信號檢測，以驗證所提方法的可行性和有效性。

1 基于勢函數特征參數調節的隨機共振

1.1 勢函數特征參數引入

經典隨機共振理論中，隨機共振現象的產生主要包括三大要素：非線性系統、滿足小參數條件的信號及噪聲。在三者的協同作用下，系統輸出信噪比會在合適噪聲強度下達到最大值，此類現象被稱為隨機共振現象。隨機共振模型可由郎之萬方程表示為

(1)

式中:A0和f0分別為周期驅動信號的幅值和頻率；n(t)為噪聲強度D的高斯白噪聲，其均值和自相關函數滿足：〈n(t)〉=0，〈n(t)n(t-τ)〉=2Dδ(τ)。U(x)為雙穩勢函數，通常表示為

式中:a和b為系統參數。勢函數的勢壘高度ΔU和勢阱間距ΔL分別為

ΔU=a2/4b

(3)

(4)

由式(3)和式(4)可知，當調節系統參數a或b時，都會導致勢函數U(x)的勢壘高度和勢阱間距同時發生變化，對勢函數的變化規律不易掌握。為了能將勢壘高度或勢阱間距分離，引入勢函數特征參數，即引入勢壘高度參數h和勢阱間距參數w來重新描述勢函數的特征。由參數h和w構建的雙穩勢函數變為

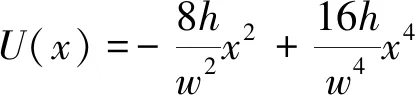
(5)

式中:h0，w0;系統參數與勢函數特征參數對應關系為a=16h/w2及b=64h/w4。根據式(3)和式(4)可得由參數h和w描述的勢壘高度ΔU和勢阱間距ΔL為

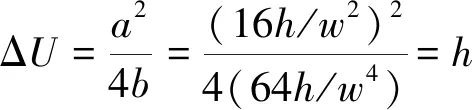
(6)

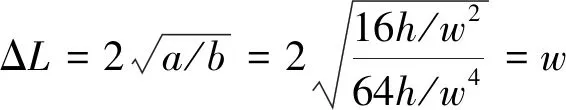
(7)

根據式(6)和式(7)可知，通過變量代換后，勢函數特征參數h和w為相互獨立互不耦合的，因此實現了勢壘高度和勢阱間距的解耦，可以分別獨立考察勢壘高度或勢阱間距對系統勢函數的影響。而現有的系統參數調節法則無法直接得到勢函數的變化規律，它屬于一種非解耦的系統參數調節方式。為了更好地說明這一點，圖1是不同參數h和w下的勢函數曲線。假設參數h=0.3和w=2得到勢函數曲線(實線)是基準曲線，那么當w=3增大勢阱間距時，將得到比基準曲線勢阱間距大而勢壘高度保持不變的勢函數曲線(短劃線)；當h=0.6增大勢壘高度時，將得到比基準曲線勢壘高而勢阱間距保持不變的勢函數曲線(圓點線)。因此，通過調節勢函數特征參數h或w可方便實現勢壘高度或勢阱間距的單獨調節。

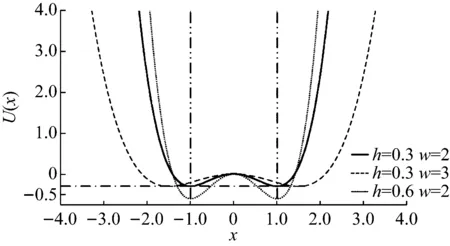
圖1 不同勢函數特征參數的勢函數曲線

1.2 勢函數特征參數對隨機共振的影響分析

根據郎之萬方程所描述的單個布朗粒子的運動行為可知，式(1)可認為是描述布朗粒子B在雙阱勢場U(x)中的運動模型，如圖2所示。圖2中的布朗粒子B，在給定的周期力和隨機力聯合驅動下，能否越過勢壘“P”點，取決勢壘高度h的大小。如果h過大，布朗粒子不會越過“P”點落入另一勢阱中，即出現“欠共振”狀態。減小勢壘高度h，布朗粒子則可能在兩勢阱間往復躍遷，即出現“雙穩隨機共振”狀態。但如果h持續減小并趨于零，勢函數也就趨于零，則式(1)會趨于一階積分系統，系統不再屬于雙穩隨機共振系統。為了能夠保證系統達到平穩規律的雙穩躍遷狀態，需要選擇合適的勢壘高度h。

而勢阱間距w則對應于布朗粒子運動的行程，關系到雙穩系統的輸出值。在其躍遷狀態下，w越大，系統輸出值也就越大。但如果持續增大w，可能會破壞粒子的雙穩躍遷狀態，因為運動行程越大，粒子運動出某個勢阱所需的時間越長，其單勢阱駐留時間也就越長。根據經典隨機共振理論[14]，系統產生雙穩隨機共振時的時間尺度匹配條件為：布朗粒子在單勢阱中的平均駐留時間要和周期驅動力的半周期時間相當。所以當過長的勢阱駐留時間與周期力的半周期時間不相當時，已有的雙穩躍遷狀態也就會被破壞。

根據勢壘高度h和勢阱間距w與雙穩隨機共振的關聯特點，下節將討論以勢壘高度為主要調節和以勢阱間距為輔助調節的最優勢壘尋優方法，以方便控制雙穩隨機共振的實現。

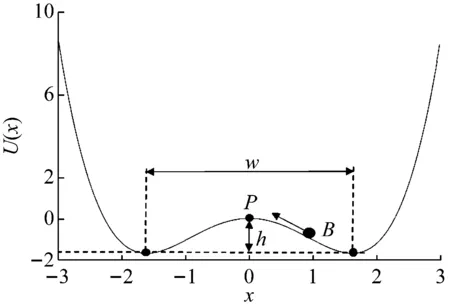
圖2 雙穩勢阱中的布朗粒子運動

1.3 基于勢函數特征參數調節的隨機共振及其信號檢測機制

根據上節勢函數特征參數的引入，隨機共振模型式(1)可改寫為

(8)

根據隨機共振理論，在噪聲、周期驅動信號和系統三者協同作用下，布朗粒子越過勢壘在雙勢阱間往復躍遷的現象被稱為隨機共振現象。其發生的條件：① 在得到部分噪聲能量的補給后，周期驅動信號的幅值要大于系統躍遷臨界值；② 布朗粒子往復躍遷時，其在某勢阱中的平均駐留時間TK(TK=1/rK，rK為Kramers逃逸速率)要與周期驅動信號周期的一半T0/2相等，即二者達到統計同步匹配的狀態。依照此條件，下面給出勢函數特征參數調節的隨機共振信號檢測方法。

首先，噪聲驅動的布朗粒子在勢阱間的躍遷速率(Kramers逃逸速率)與勢函數參數的關系可表示為

(9)

假設某待檢測信號的特征頻率為ft，則根據時間尺度同步匹配條件有

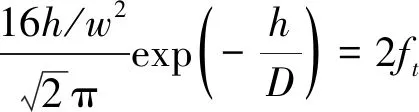
(10)

因頻率ft已知，噪聲強度D可通過對輸入信號進行估計得到，則勢壘高度h與勢阱間距w之間的關系可由式(10)確定，當h給定時w也就可以相應得到，反之亦然。二者可構成勢函數參數對(h,w)。將每組參數對代入隨機共振模型式(8)中，以四階Runge-Kutta法數值求解可得到系統輸出結果。因此，該方法可通過勢壘高度h一個參數的調節，實現對信號的檢測。而傳統的參數調節法則需要同時對系統參數a和b進行非解耦的調節，其計算相對復雜。

其次，以系統輸出信噪比作為系統是否進入雙穩隨機共振狀態的判定指標。系統輸出信噪比定義為

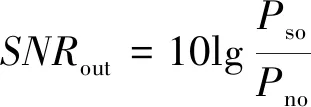
(11)

式中:Pso為輸出信號的功率;Pno為輸出噪聲的功率。根據每組勢函數參數對(h,w)由式(11)可求得相應的系統輸出信噪比，選取最大輸出信噪比對應的參數對作為系統的勢函數特征參數，代入式(8)中并進行數值求解得到系統的隨機共振輸出。

需要說明的是，勢壘高度調節的搜索步長Δh以及搜索范圍設置要考慮采樣頻率的大小。因為數值計算的步長通常取為1/fs，在數值計算過程中，原始信號的幅值會按照1/fs削弱。而合適的勢壘高度的數量級與削弱后的信號幅值相當，才可能保證系統、信號及噪聲協調匹配的隨機共振輸出。因此采樣頻率越大時最優的勢壘高度也越小。因本文研究的目標信號為微弱信號(幅值小于1)，故勢壘高度h的搜索范圍可設定為(0,1/fs)，而勢壘高度的搜索步長Δh越小，則可以得到最優勢壘高度值越精確。

下面以含噪信號檢測為例給出說明。令輸入信號中的高斯白噪聲強度為0.2，周期信號的幅值為0.05，信號頻率為0.05 Hz。采樣頻率為5 Hz，數據點數為1 000。原始信號的時域和頻域波形,如圖3所示。由于背景噪聲的存在，輸入信號的信噪比(-25.26 dB)較低，因此從頻域圖中無法清晰識別出該周期信號。

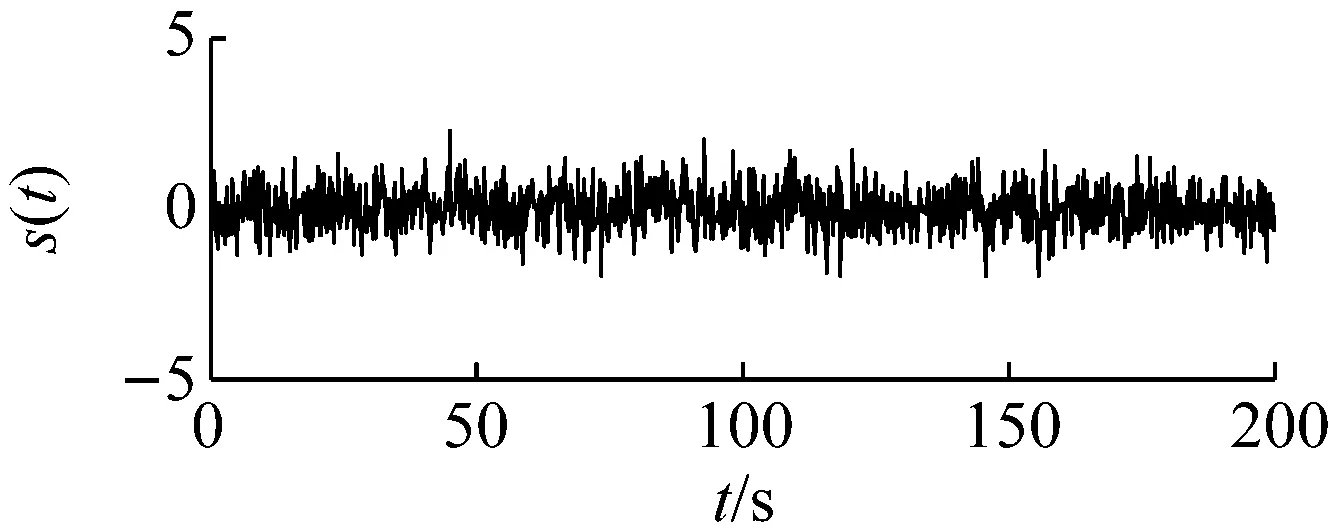
(a)

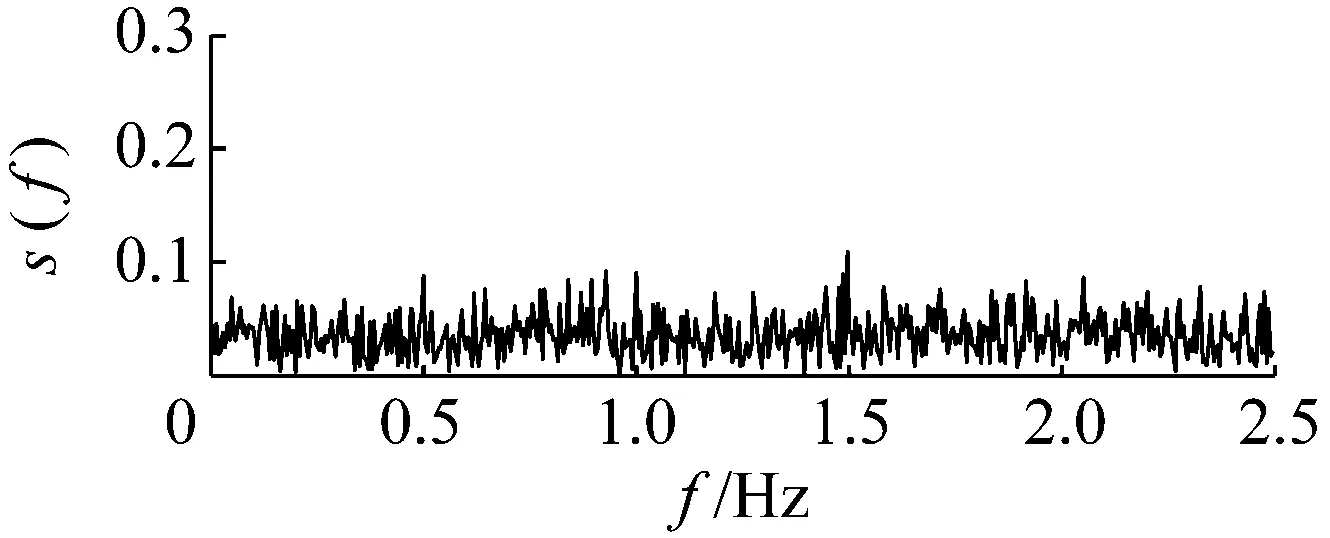
(b)

設定勢壘高度h的搜索范圍在(0,0.2)區間，搜索步長Δh=0.001，于是得到最大輸出信噪比(-9.87 dB)對應的最優勢函數特征參數為h=0.015和w=0.708。將此參數對(0.015, 0.708)代入式(8)計算得到系統輸出響應的時頻圖,如圖4所示。從圖4可知,0.05 Hz周期信號的特征譜線。

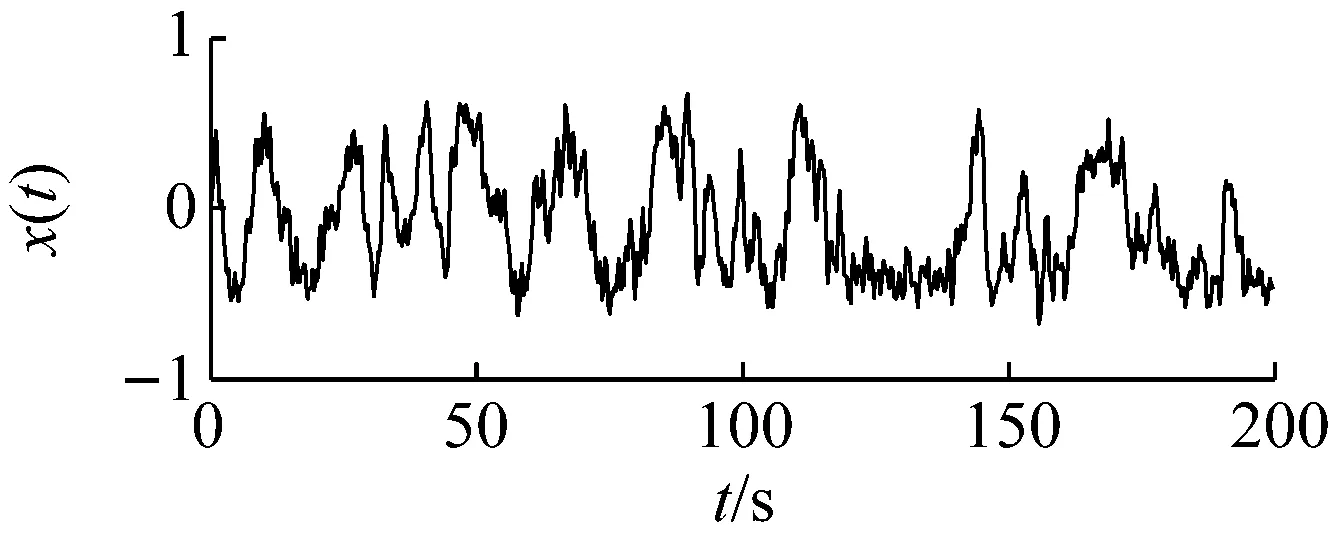
(a)

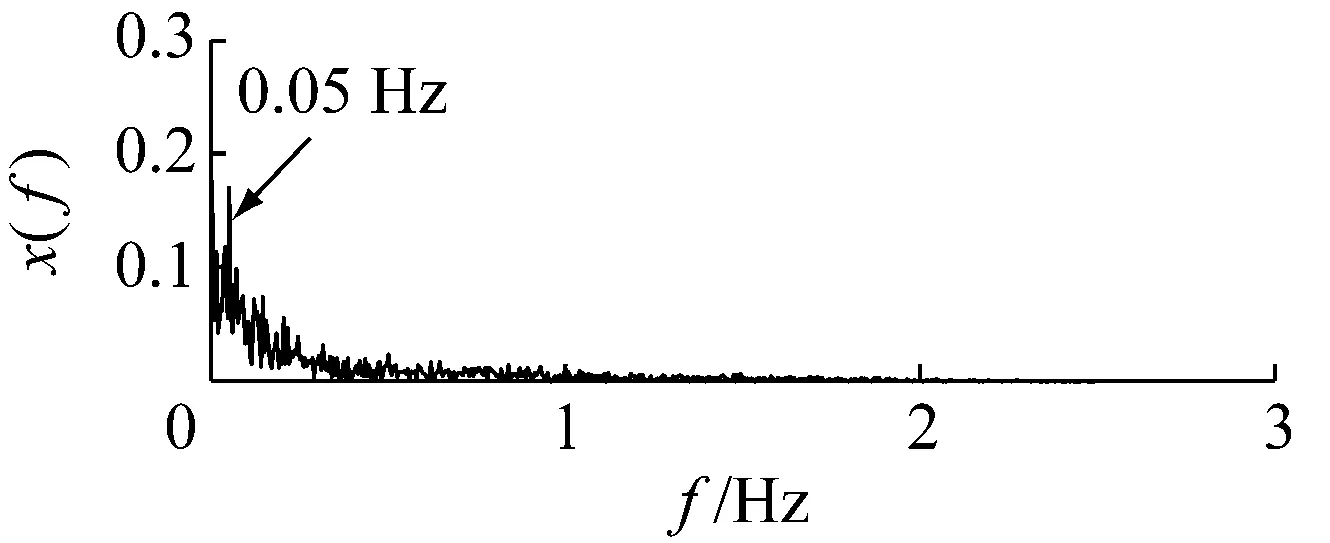
(b)

2 低采樣頻比的頻域信息交換技術

對于采樣頻率與特征信號頻率之比小于50的低采樣頻比信號，其雙穩響應通常很難達到隨機共振狀態。為解決此問題，本文引入FIE來實現低采樣頻比的隨機共振。所謂頻域信息交換，實際上就是將處在高頻段的特征信號通過單邊帶調制方法與低頻段信息交換，以滿足隨機共振對采樣頻比的要求。由于文獻[12]在頻域信息交換時首先采用快速傅里葉變換得到頻域信息，因此不可避免地會存在頻譜泄露的問題。為了克服這一問題，本文探討了基于濾波器技術的時域換頻方法，其原理流程如圖5所示。由圖5可知,基準低頻信息sl(t)是指采樣頻率fs與信號頻率之比大于50的頻段處信息。令基準低頻為fl，且令基準低頻信息sl(t)的頻域范圍為(0,B)，則fl∈(0,B)且fs/B50。相應的目標信號st(t)的頻帶為(ft-fl,ft-fl+B)，ft為目標信號的特征頻率，則單邊調制時的載波頻率為ft-fl。為避免信號處理過程出現頻帶重疊，文中所采用低通濾波器的通帶必須和高通濾波器的阻帶相同，取為(0,B)；帶通濾波器的通帶也要和帶阻濾波器的阻帶相同，取為(ft-fl,ft-fl+B)。因此，低通、帶通濾波器的通帶帶寬與高通、帶阻濾波器的阻帶帶寬相同，均為B。

需要說明的是，之所以采用高通、帶阻濾波器濾除基準低頻和目標信號頻率處的信息來獲取剩余信號信息，是因為在用低通、帶通濾波器提取基準低頻和目標信號的信息時，信號的相位會發生變化，因此不能將原信號直接減去提取的基準低頻和目標信號信息來獲取剩余信號信息。此外，為了能夠有效提取特征頻率處的信息，本文采用橢圓濾波器對目標信號進行濾波，因為橢圓濾波器比巴特沃斯、切比雪夫等濾波器具有更窄的過渡帶。

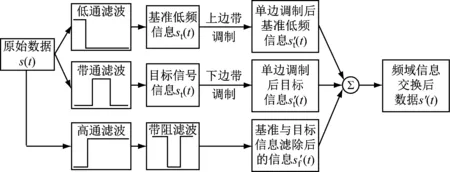
圖5 頻域信息交換流程圖

假設低通、高通、帶通和帶阻濾波器分別用LPF、HPF、BPF和BSF表示。通過用LPF、BPF可以分別提取出基準低頻信息sl(t)以及目標信號信息st(t)，通過HPF和BSF濾波器得到基準信息和目標信息濾除后的信息sf(t)，即有

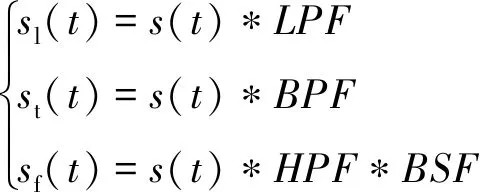
(12)

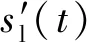
(13)

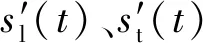
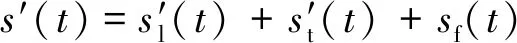
(14)

由式(14)可知，因頻域信息交換處理數據s′(t)中的特征信號頻率與采樣頻率之間的頻率間距增大，其采樣頻比超過了50，因此為實現雙穩隨機共振達到檢測特征信號的目的而創造了條件。

3 基于勢函數特征參數調節和頻域信息交換的隨機共振信號檢測

將勢函數參數調節方法與頻域信息交換技術相結合，既可以直觀理解勢壘或勢阱變化對隨機共振的影響，又能夠克服采樣頻比對隨機共振的限制，因此頻域信息交換與勢函數參數調節的結合將有助于信號隨機共振的檢測實現。這一信號檢測方式的流程圖，如圖6所示。其執行過程是：首先將原始數據進行頻域交換，將高頻段的目標特征信號交換到基準低頻處，得到換頻后的數據s′(t);然后將數據s′(t)輸入到勢函數特征參數調節的隨機共振系統中進行處理，其相應的隨機共振模型由式(8)變為

(15)

圖6 基于勢函數特征參數調節SR和頻域信息 交換的信號檢測流程圖

按照“1.2”節勢函數特征參數的調節方法，找出最大輸出信噪比對應的特征參數對，并代入式(15)中，數值得到系統的隨機共振響應，檢測出基準低頻處的目標信號。最后將檢測出的信號進行頻域信息恢復，得到實際目標信號的檢測結果。

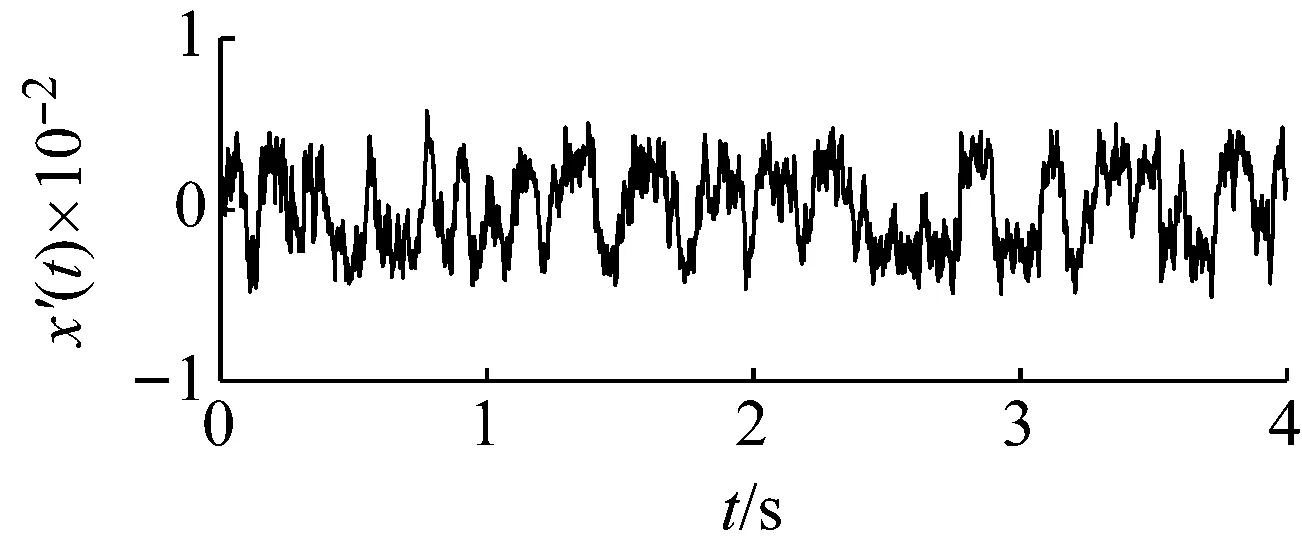
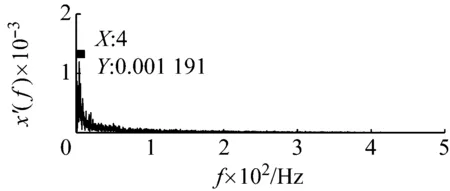
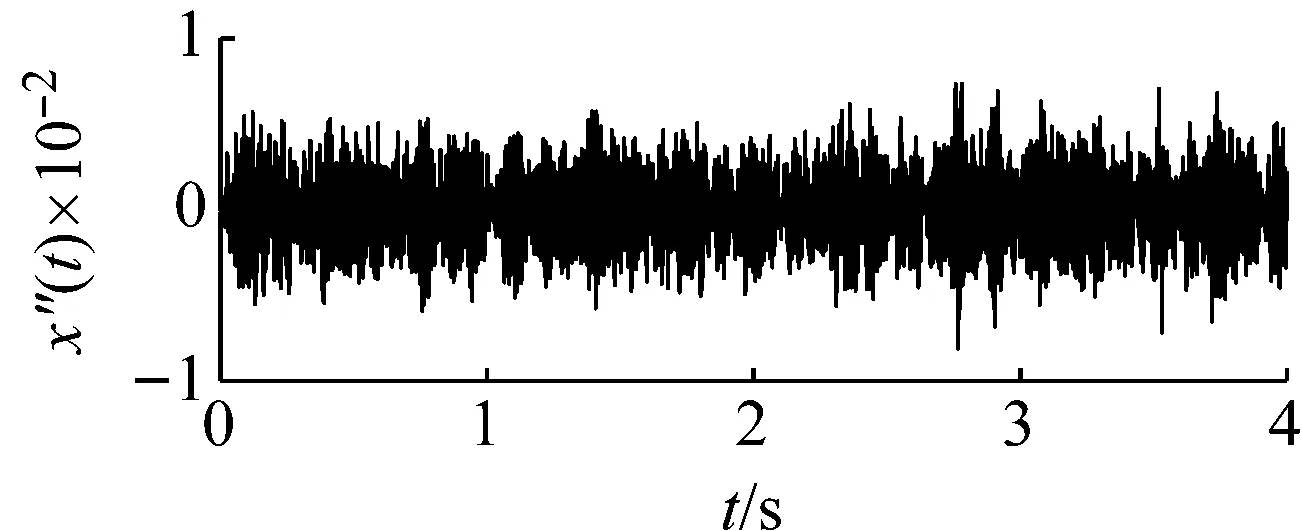
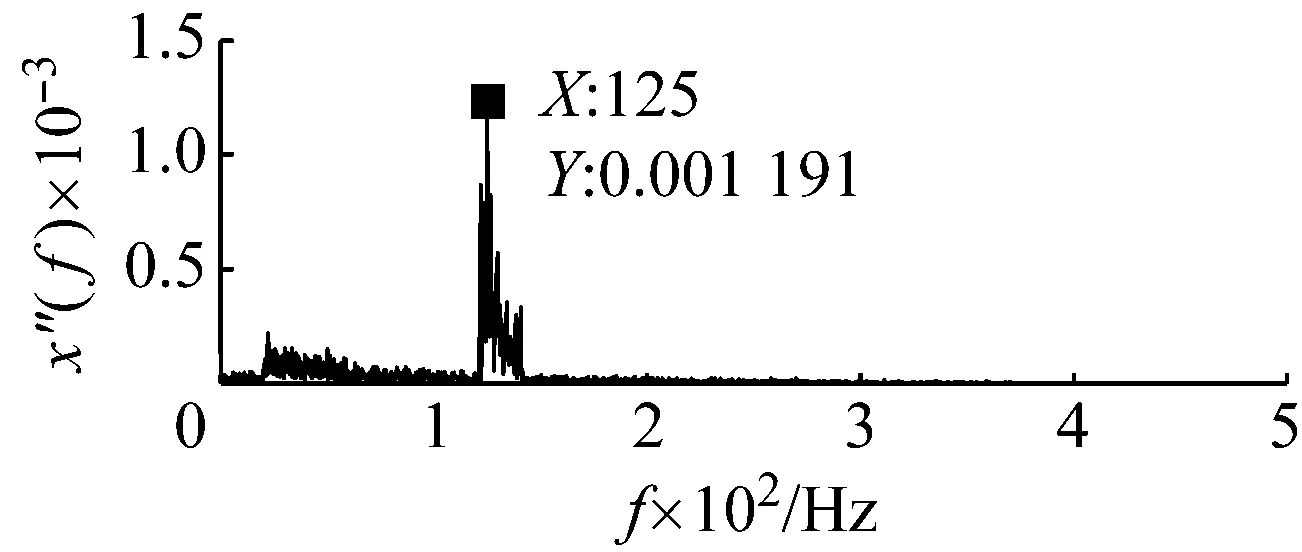
以含噪信號檢測為例進行說明。令周期信號的幅值和頻率分別為0.05和125 Hz，噪聲強度為0.2。數據采集長度為4 000，采樣頻率為1 000 Hz。原始輸入信號如圖7所示。顯然背景噪聲中的原始輸入信號不可識別。如果直接采用勢函數特征參數調節的隨機共振方法對輸入信號進行處理，得到最優勢函數參數的系統響應如圖8所示。從圖8的頻譜中無法確認125 Hz特征信號的存在，這是由于信號的采樣頻比1 000/125=8小于50造成的。下面采用頻域信息交換(換頻)和勢函數特征參數調節的隨機共振方法處理。

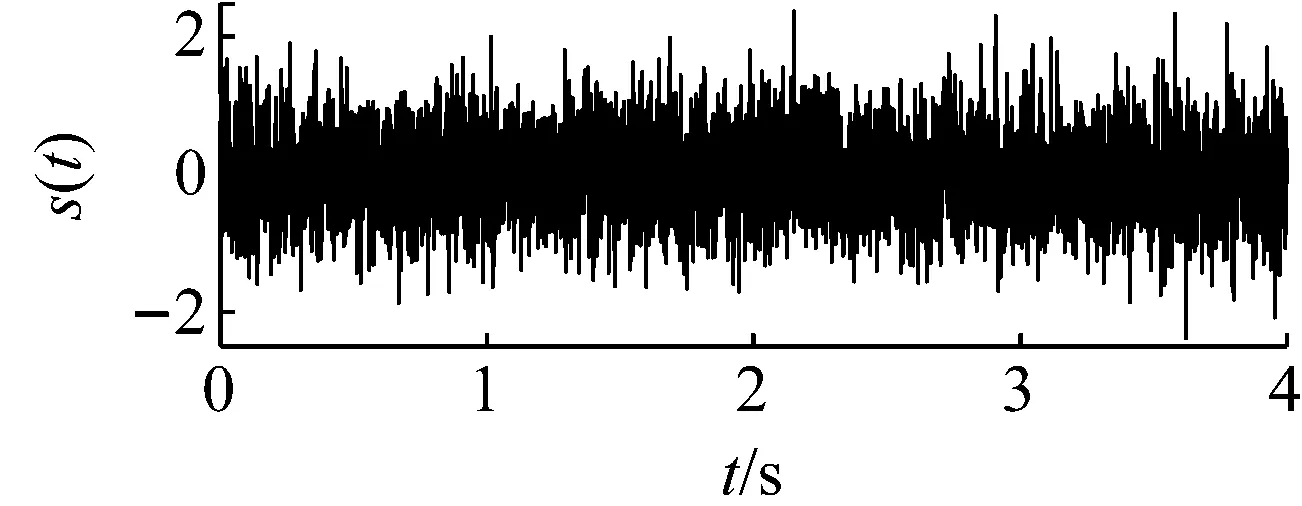
(a)

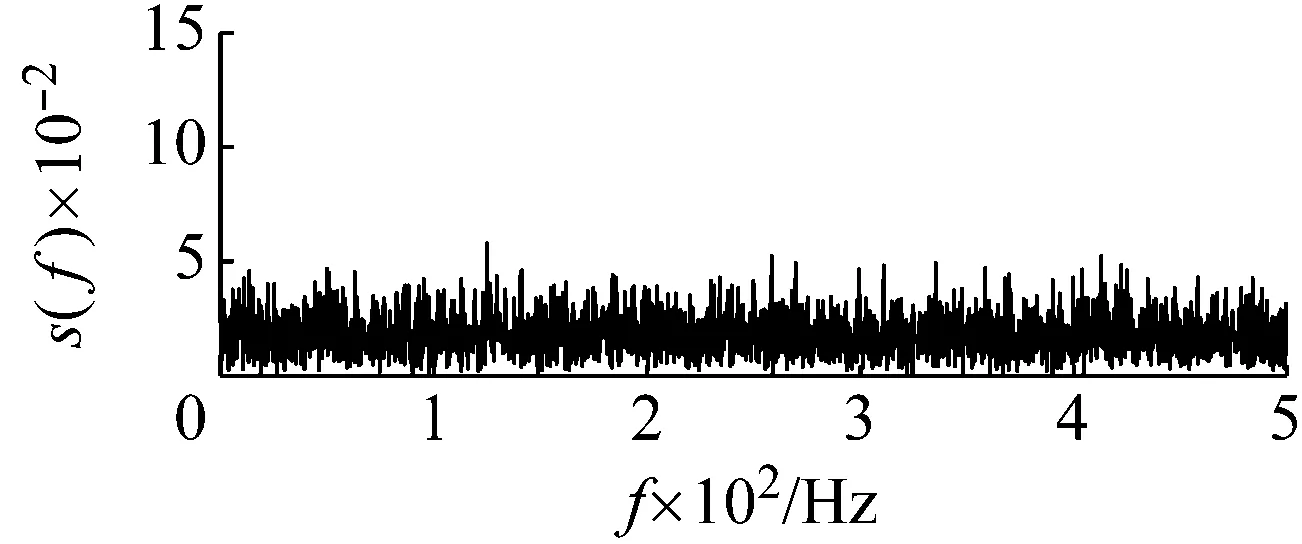
(b)

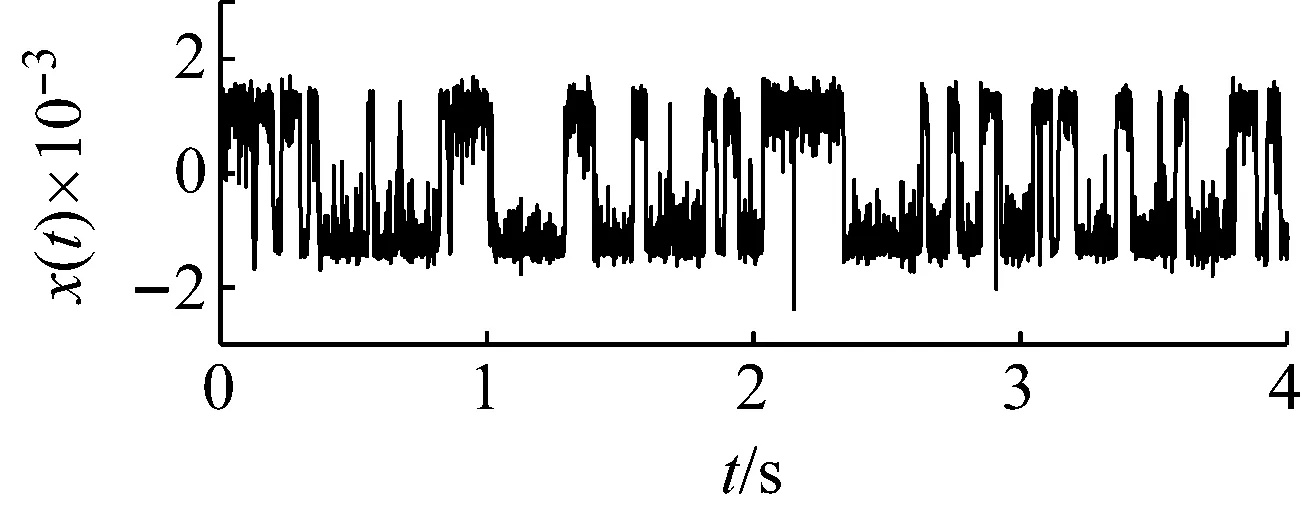
(a)

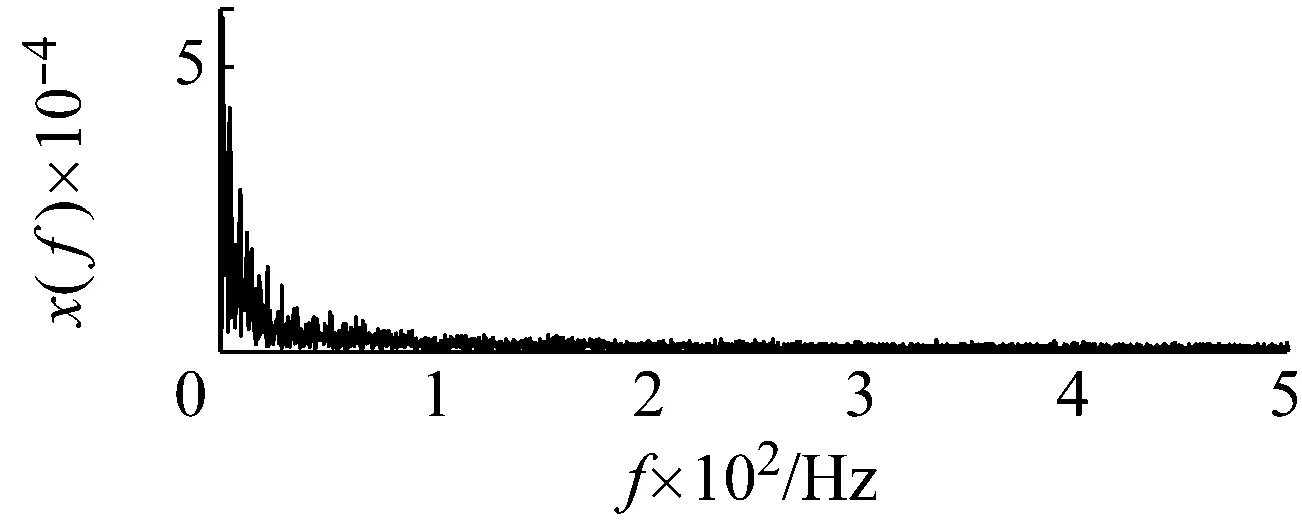
(b)

首先令基準低頻為4 Hz，基準低頻信息的頻帶為(0,20 Hz)，則目標信號所在的頻帶應為(121 Hz,141 Hz)，調制載頻為121 Hz。頻域信息交換后，對數據進行隨機共振處理得到最優勢函數特征參數(h=0.000 06,w=0.005 3)的系統輸出如圖9所示。從圖9(b)可知，在基準低頻4 Hz處有明顯的譜線。通過頻域信息逆交換恢復后，可確認125 Hz目標信號的存在，如圖10所示。

4 動車轉向架軸承故障診斷

4.1 轉向架軸承模擬實驗臺

由于材料缺陷，加工或者裝配不當，潤滑不良，水分或者異物侵入等原因都可能導致轉向架軸承的損壞。即使在裝配和使用維護都正常的情況下，經過長時間、高速、負載運行后，軸承也會出現疲勞剝落和磨損等現象，影響列車的正常工作。本文以CRH380BL動車組所采用的轉向架軸箱軸承的內、外圈及滾動體點蝕剝落故障為研究對象進行分析。該轉向架軸箱軸承由舍弗勒公司提供，圖11是軸承故障測試實驗臺。為了模擬滿載(17 t)工況下軸承的運行狀態，本實驗臺利用螺栓框架結構壓縮三根彈簧，彈簧的彈力再通過半圓端蓋與軸承外圈的接觸，對軸承施加載荷，如圖11負載部分所示。CRH380BL動車組設計最高時速可達380 km，試驗中測試時速為260 km，對應的轉子轉速為1 590 r/min，即轉頻 等于26.5 Hz。將加速度傳感器布置在半圓端蓋上測試軸承的振動信號，使用NI PXI-1033信號采集儀對軸承振動信號進行采集，采樣頻率設為5 000 Hz，采樣時間為2 s。表1給出了軸承的主要參數。

(a)

(b)

(a)

(b)

表1 滾動軸承主要參數

圖11 轉向架軸承測試實驗平臺

4.2 軸承故障分析

4.2.1 外圈故障分析

以軸承外圈輕度點蝕剝落故障為例，對外圈內表面加工故障。輕度故障對應的平均加工深度為：0.18～0.27 mm。

軸承外圈的故障特征頻率可由下式給出

(16)

式中,fi為轉子轉頻26.5 Hz，其他參數可參考表1，經計算可得到外圈對應故障頻率理論值為193.8 Hz。

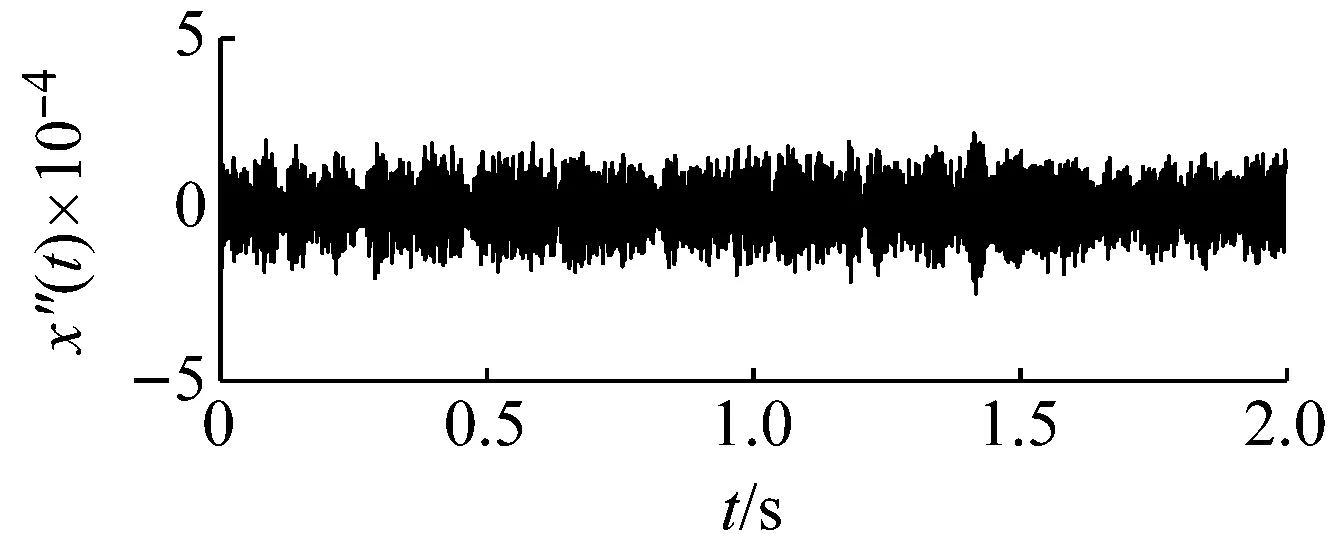
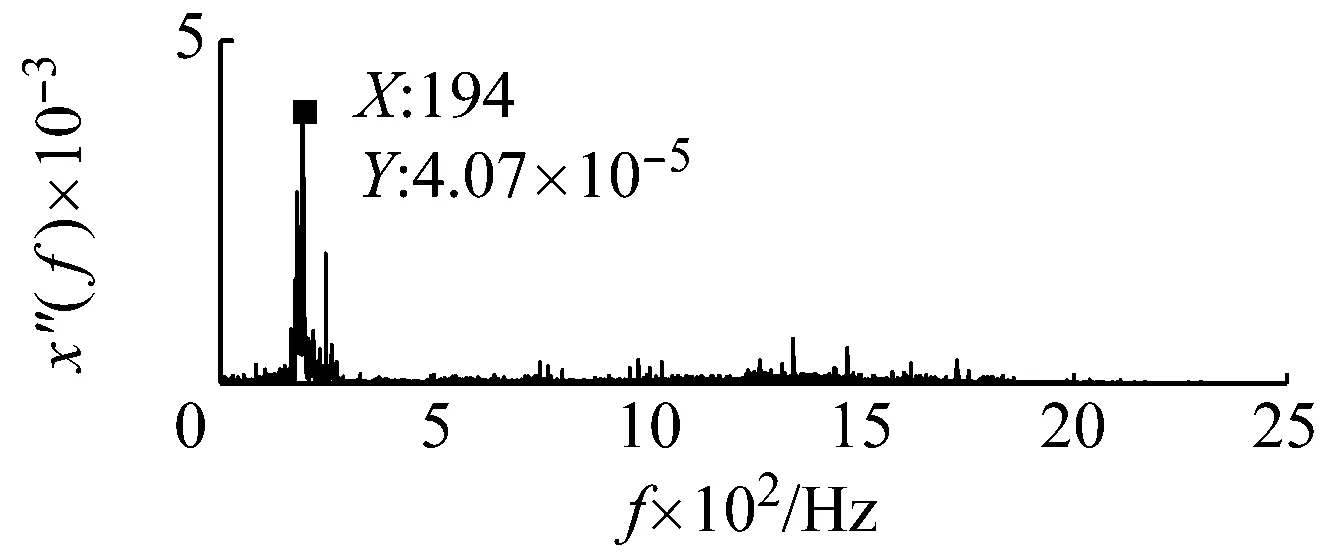
圖12為外圈故障的原始采集信號，由于較強的高頻成份及背景噪聲的存在，故障信號比較微弱，而無法判定故障的存在。采用本文提出的基于頻域信息交換和勢函數特征參數調節的隨機共振信號檢測方法對其進行處理。首先根據頻域信息交換思想，基準低頻頻率選為10 Hz，低頻頻帶為(0,100 Hz)，則目標信號的所在頻帶為(183.8 Hz,283.8 Hz)，相應的載頻為183.8 Hz。然后噪聲強度值估算約為0.07。由于采樣頻率和信號頻率較大，勢壘調節步長相應設置為1×10-7，得到最優勢壘高度和勢阱間距參數對為(4×10-7，1.9×10-4)。將勢函數特征參數對代入隨機共振模型式(15)，得到系統響應如圖13所示。在基準低頻10 Hz處可以看出明顯的譜峰。將頻域信息恢復，譜峰相應出現在194 Hz處，如圖14所示。即可判定外圈故障的存在。

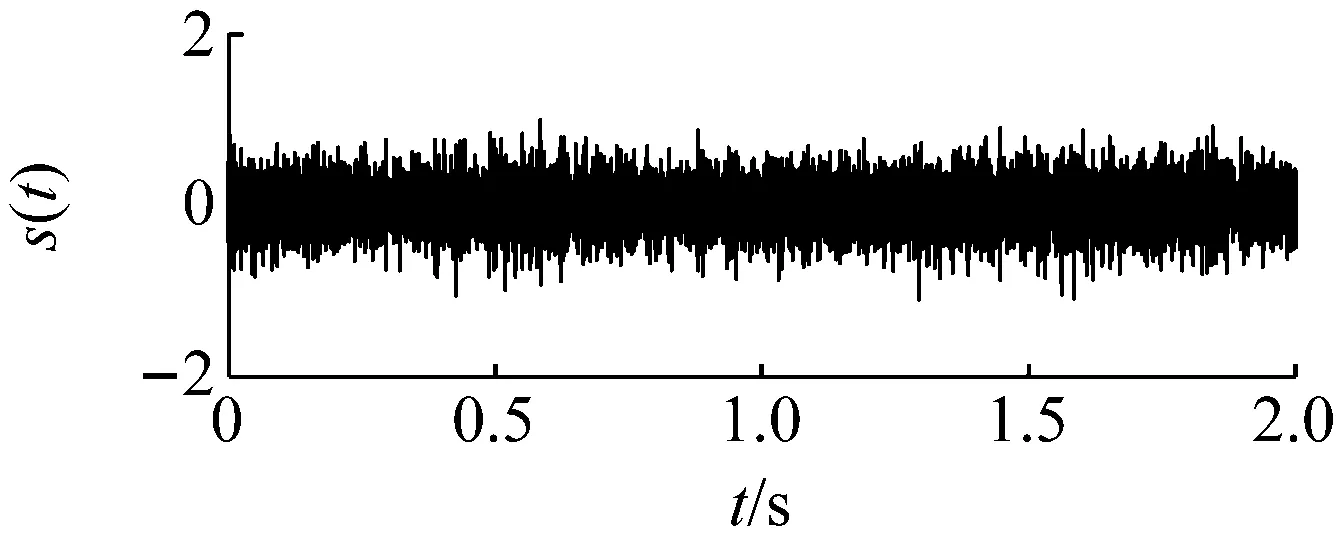
(a)

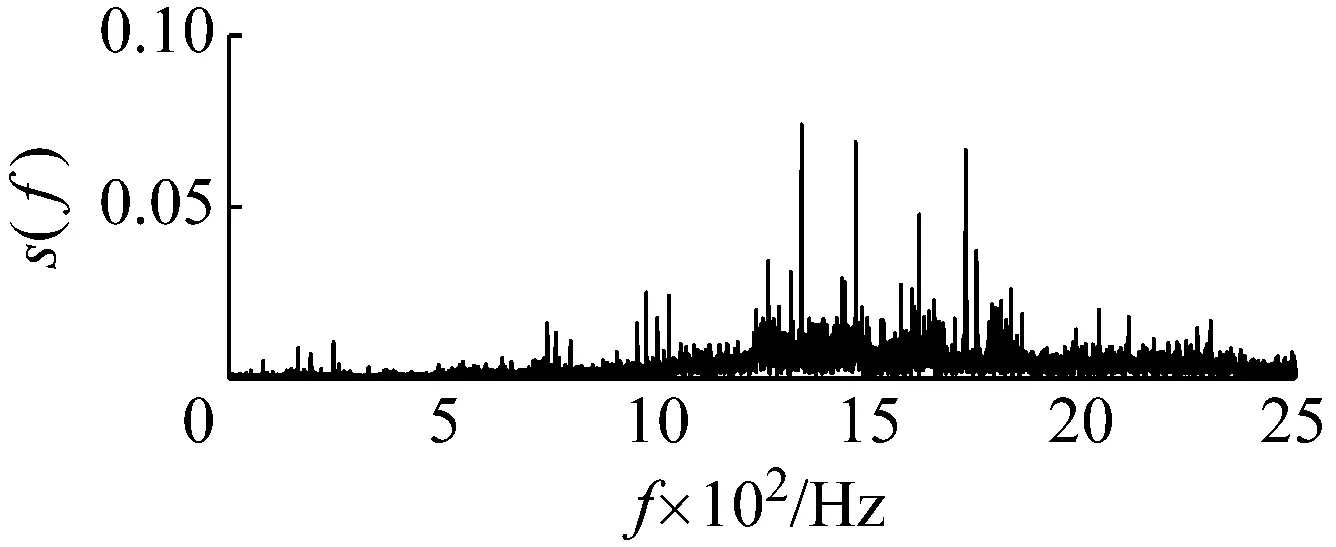
(b)

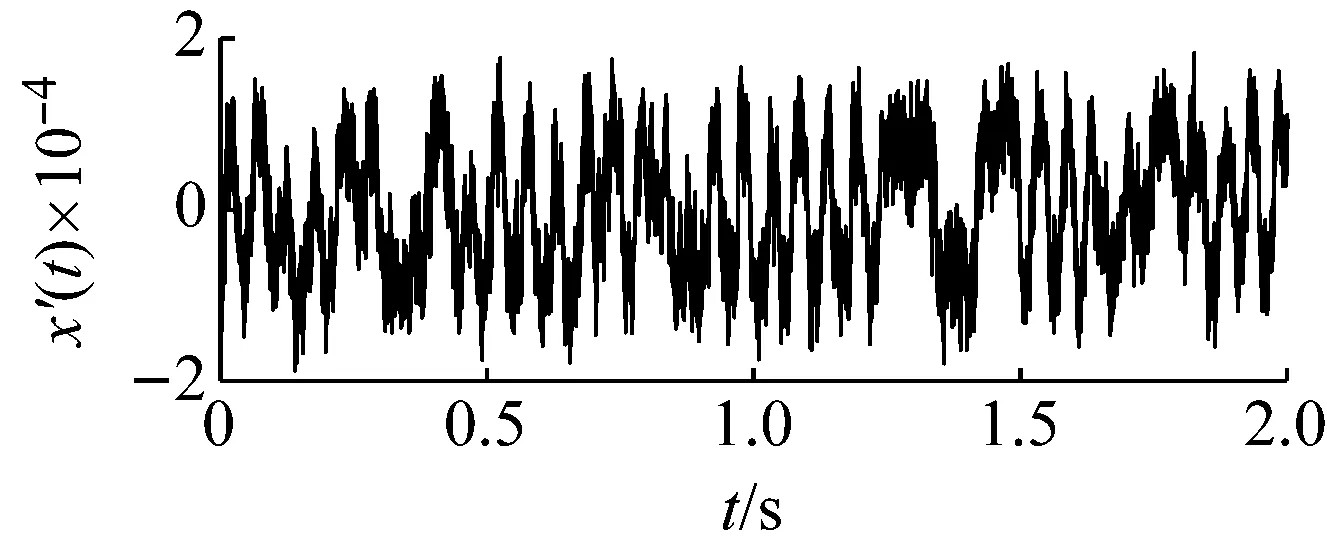
(a)

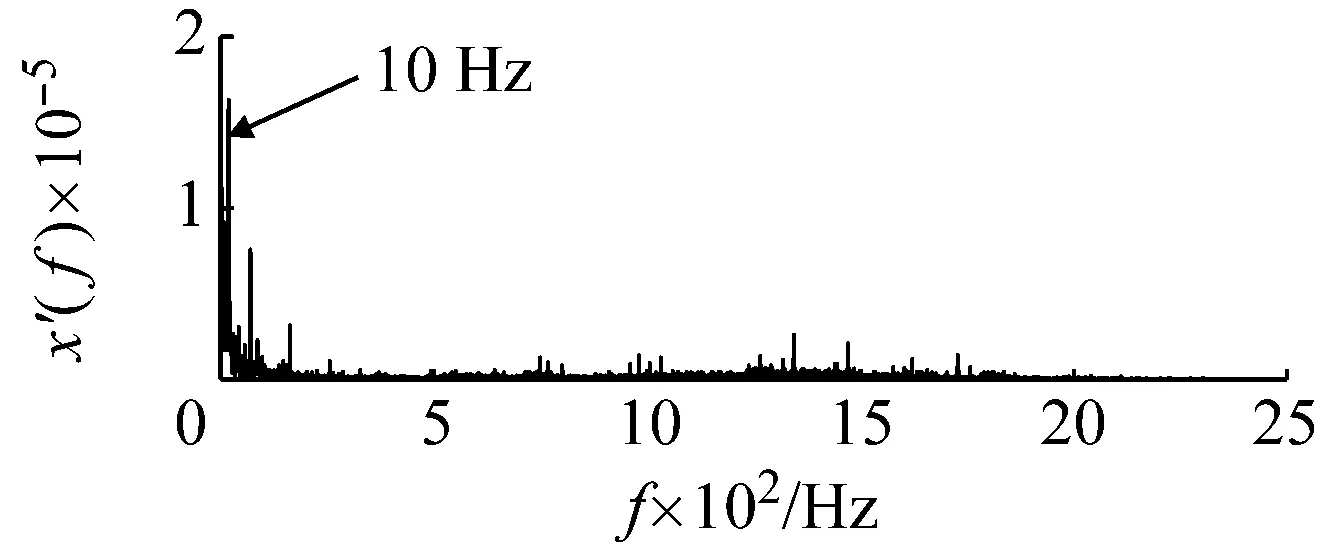
(b)

(a)

(b)

4.2.2 內圈故障分析

以內圈表面中度剝落故障為例進行分析。中度剝落故障的平均剝落深度為0.6 mm，剝落沿內圈軸線方向。同樣軸承內圈的故障特征頻率可由下式給出

(17)

式(17)的參數與式(16)參數相同，可算出內圈對應故障頻率的理論值為256.7 Hz。

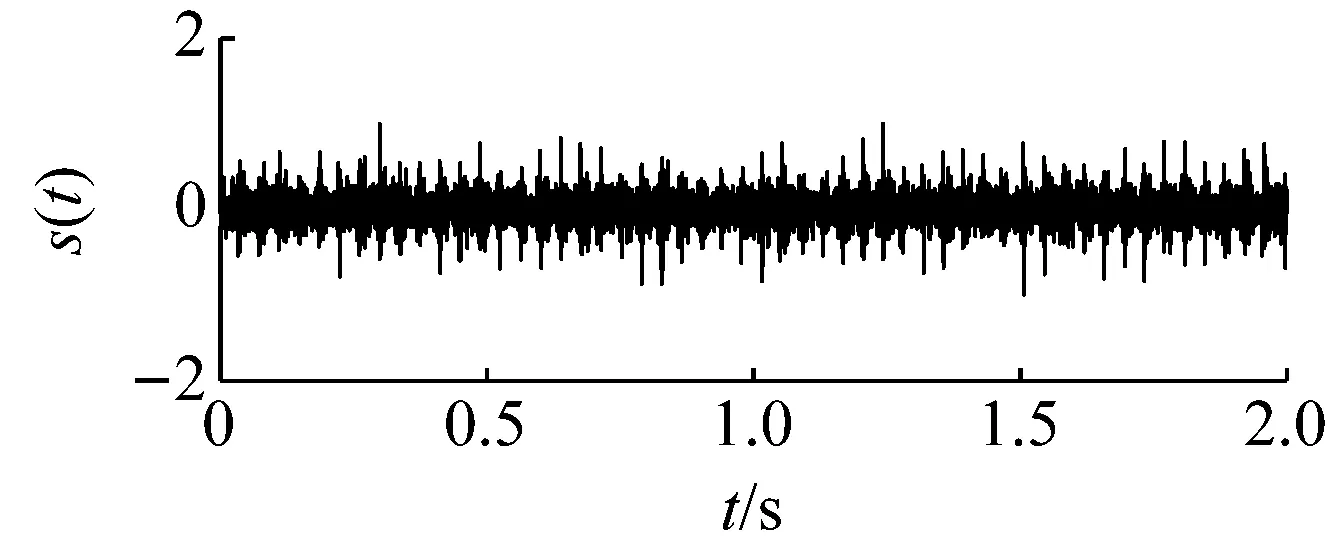
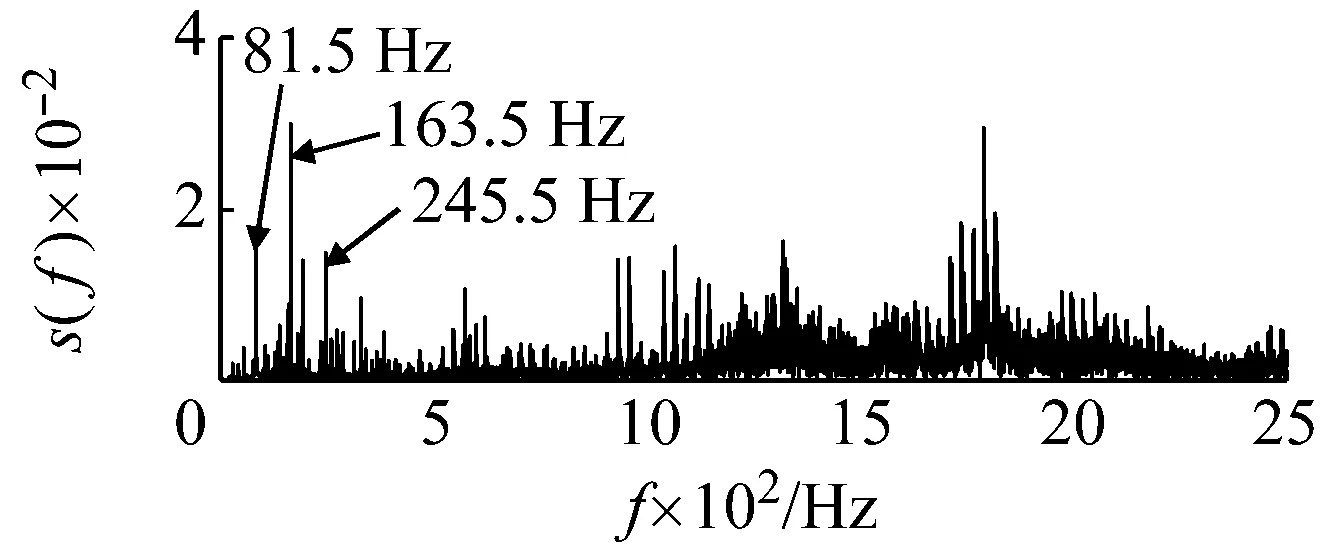
當軸承存在內圈故障時，內圈周期性回轉運動會激起支撐軸承系統的振動，如81.5 Hz、163.5 Hz以及245.5 Hz處存在明顯的譜線，此外還會激起軸承系統的高頻固有振動。因此，內圈故障特征頻率會受到復雜的調制而不能從頻譜中識別出來，如圖15所示。

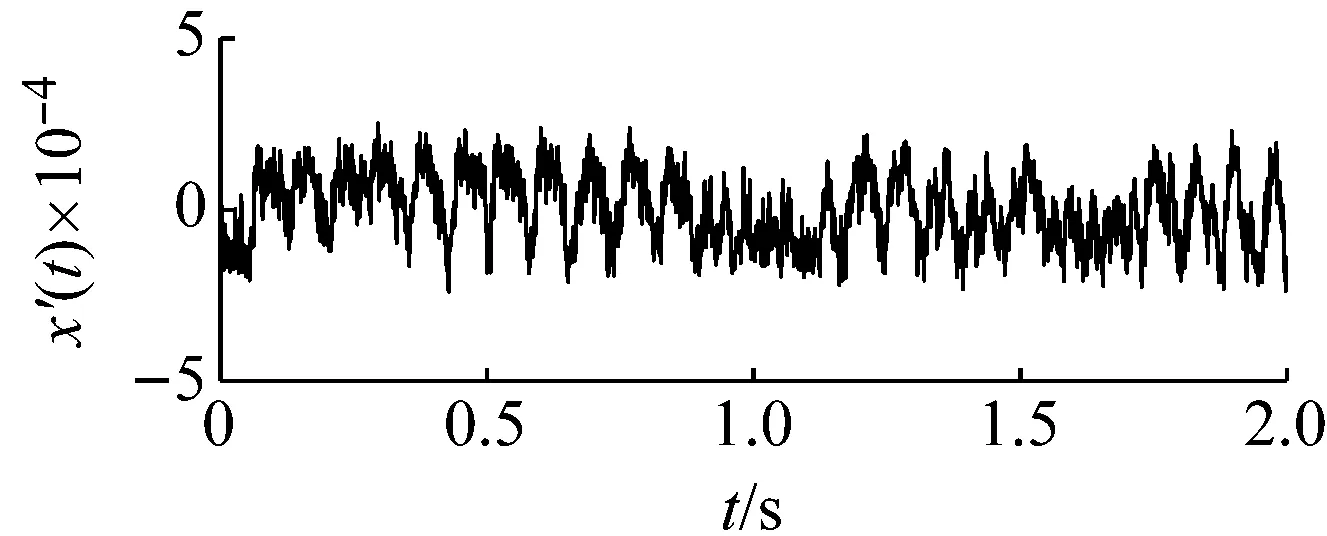
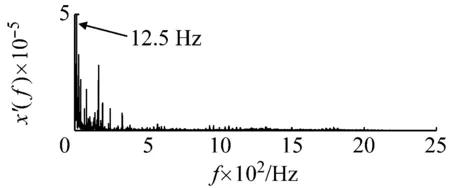
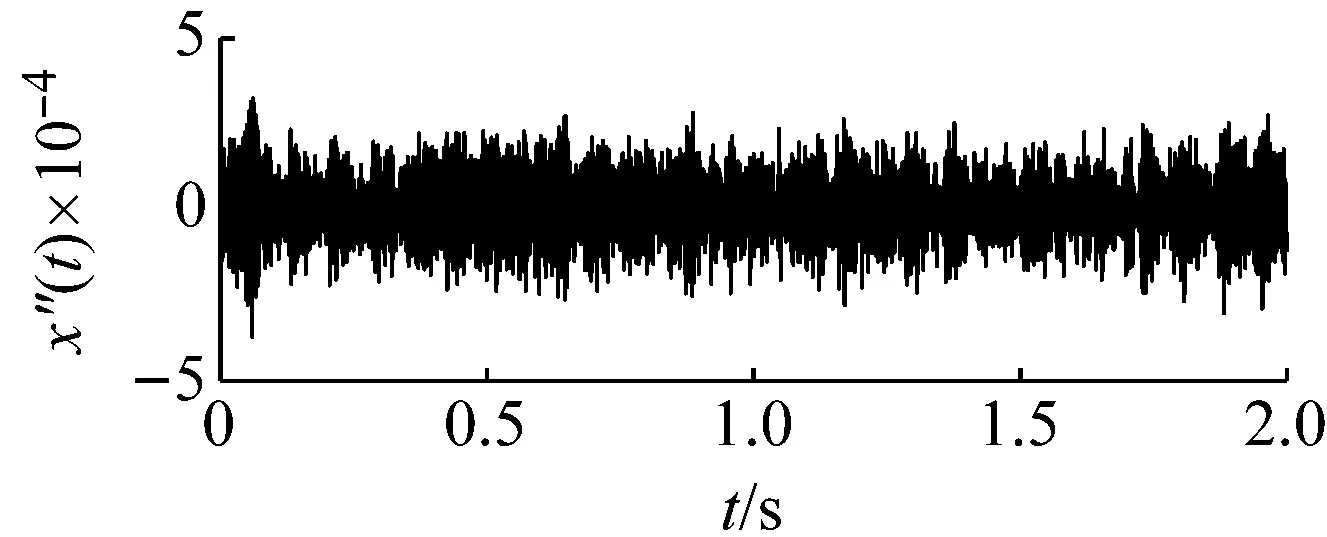
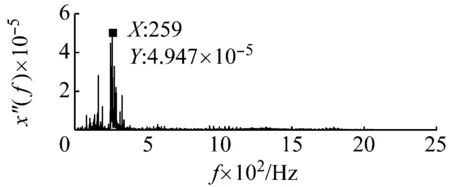
采用本文提出的方法對其進行處理。基準低頻頻率以及低頻頻帶選擇與外圈故障采用的頻率和頻帶相同。因此內圈故障特征信號所在頻帶為(246.7 Hz,346.7 Hz)，相應的載頻為246.7 Hz。原始采集信號噪聲強度估算約為0.012 7。同樣由于采樣頻率和信號頻率較大，勢壘調節步長相應設置為1×10-7，得到最優勢壘高度和勢阱間距參數對為(3×10-7，2.4×10-4)。將PFCPs對代入SR模型式(15)，系統響應如圖16所示。在頻率12.5 Hz處可以看出明顯的譜峰。根據頻域信息恢復后的頻譜圖17，可發現在259 Hz處出現了明顯的譜峰，與理論計算值256.7 Hz非常接近，因此可判定內圈故障的存在。

(a)

(b)

(a)

(b)

(a)

(b)

4.2.3 滾動體故障分析

以滾動體表面中度剝落故障為例進行分析。滾動體中度平均剝落深度為0.4 mm。軸承滾動體的故障特征頻率可由下式給出

(18)

式(18)的參數與前兩節采用的參數相同，可算出滾動體對應故障頻率的理論值為92.6 Hz。

圖18為采集的滾動體原始信號，可以看出由于系統存在豐富較強的高頻成份，包含滾動體故障特征頻率的低頻成份受到了較大壓制而無法識別。同時在滾動軸承運行時，除了滾動體自身的旋轉外還伴隨有保持架的轉動。因此當滾動體存在故障時，其故障頻率會受到保持架旋轉頻率的調制。根據保持架旋轉頻率公式fc=1/2(1-d/Dcosβ)fi和前文給定參數，可以計算出保持架的旋轉頻率約為11 Hz。因此調制后的滾動體故障頻率可能為103.6 Hz，其二倍頻成份可能調制到196 Hz附近。以103.6 Hz為目標信號進行檢測，基準低頻頻率同樣設定為10 Hz，低頻頻帶為(0，100 Hz)。則目標信號的頻帶為(93.6 Hz,193.6 Hz)，相應的載頻為93.6 Hz。噪聲強度估算約為0.000 23。勢壘調節步長相應設置為1×10-8，得到最優勢壘高度和勢阱間距參數對為(0.8×10-7，1.13×10-4)。將PFCPs對代入SR模型式(15)，得到圖19的系統響應時域、頻域圖，在頻率10 Hz處具有明顯的譜峰。圖20為頻域信息恢復后的時域、頻譜圖，可發現在103.5 Hz和195 Hz處都出現了明顯的譜峰，可認為是被保持架頻率調制后的滾動體故障信號，即可判定滾動體故障的存在。

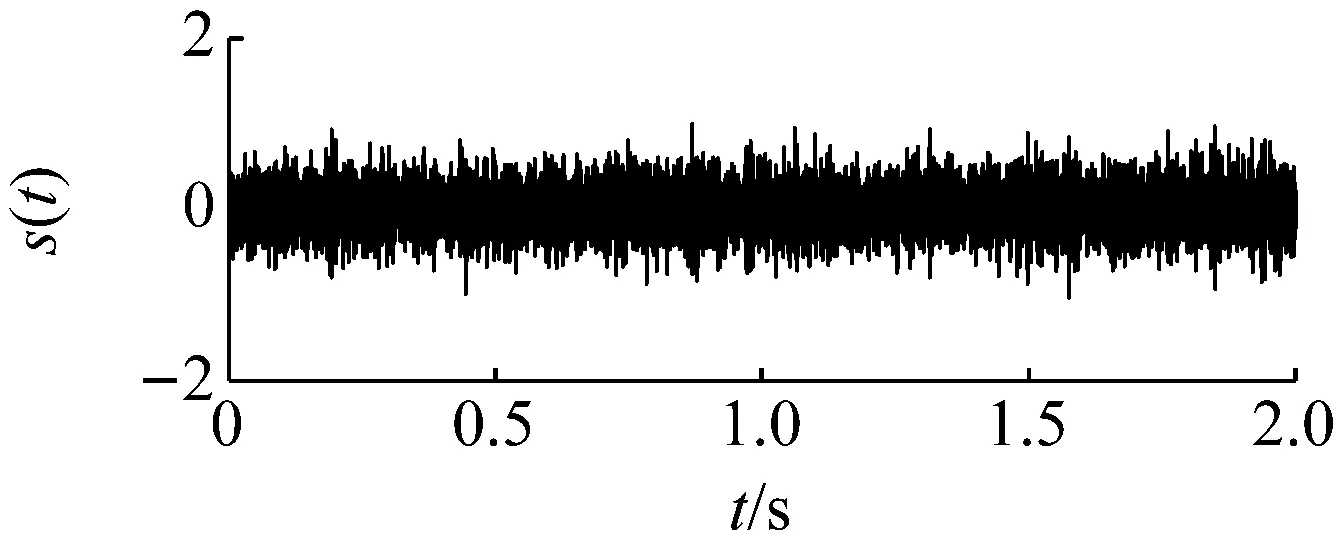
(a)

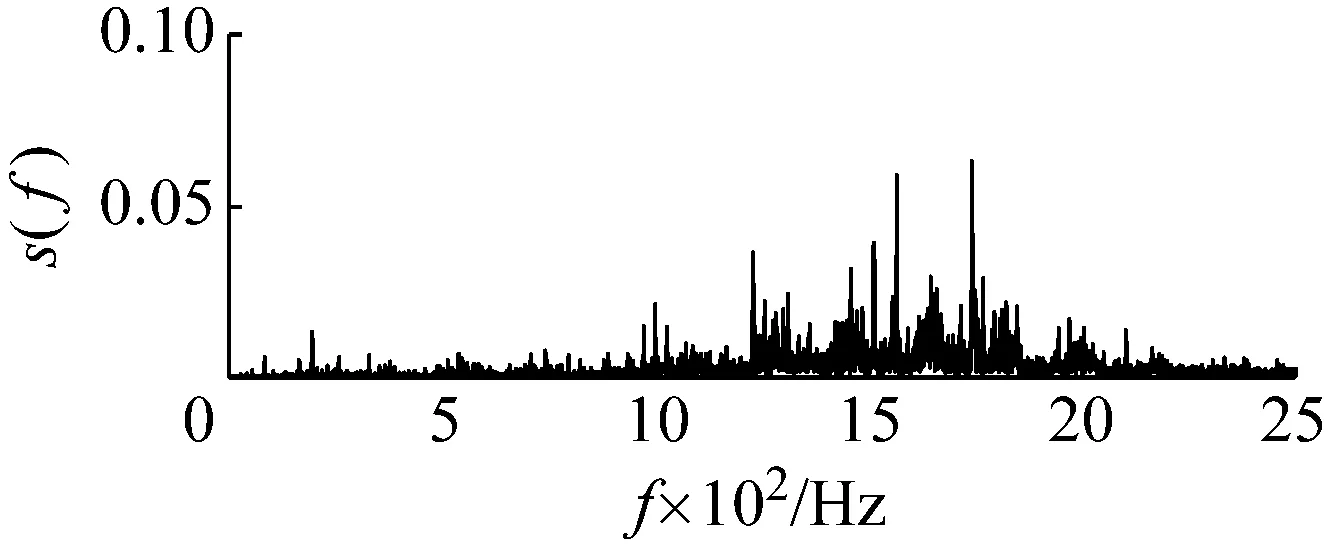
(b)

5 結 論

利用SR理論檢測微弱信號時，為使系統達到SR而產生最佳的輸出，不可避免地涉及到系統參數調節。

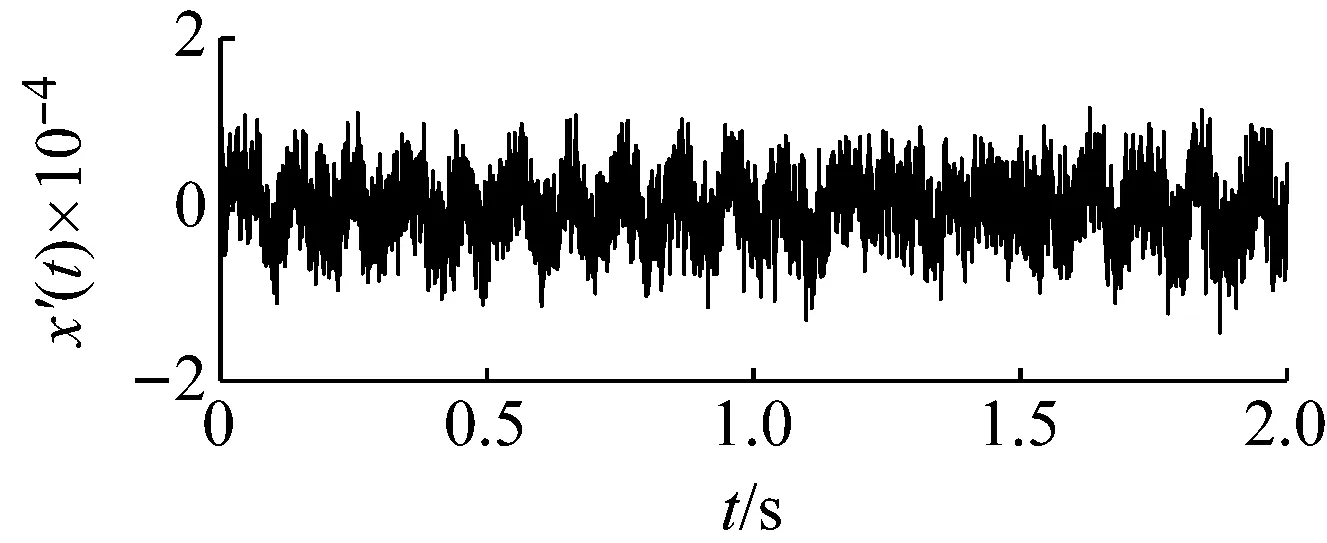
(a)

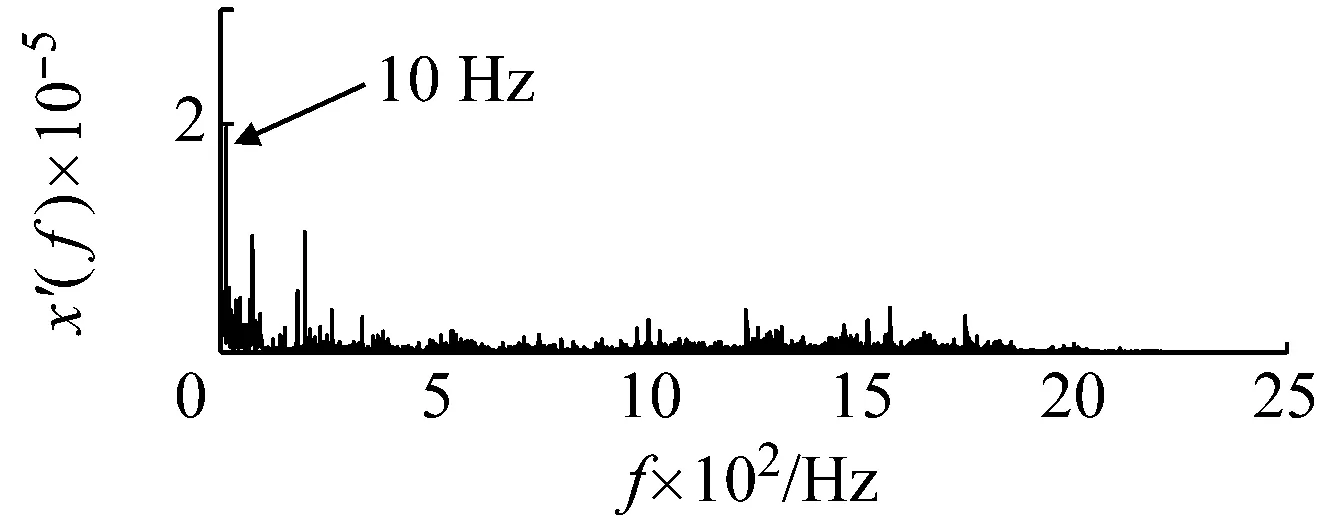
(b)

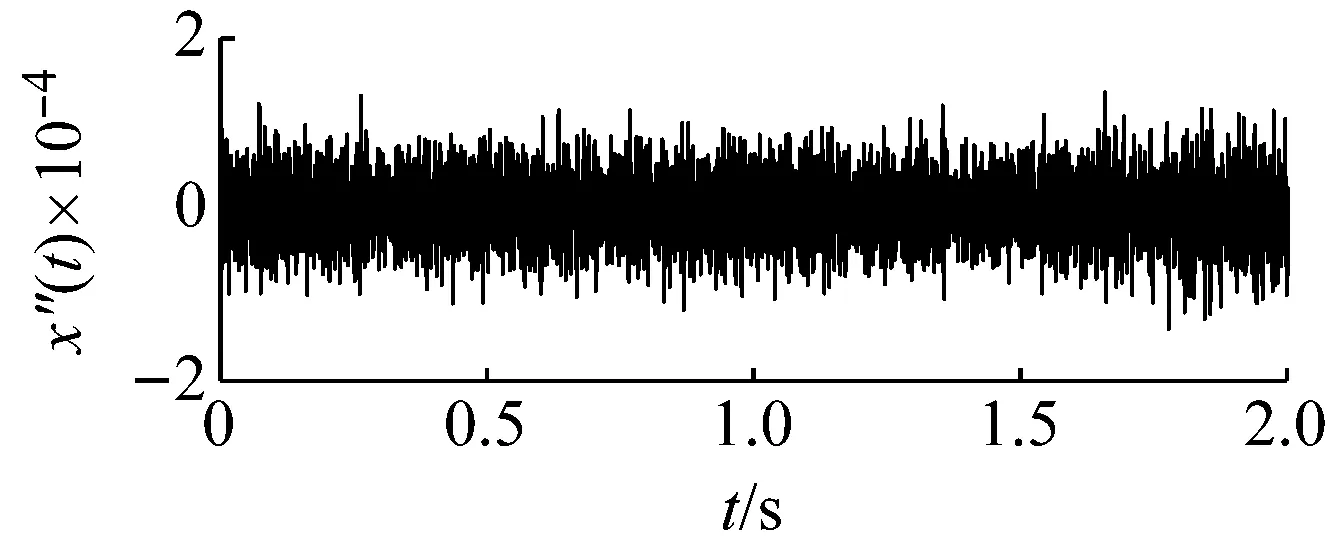
(a)

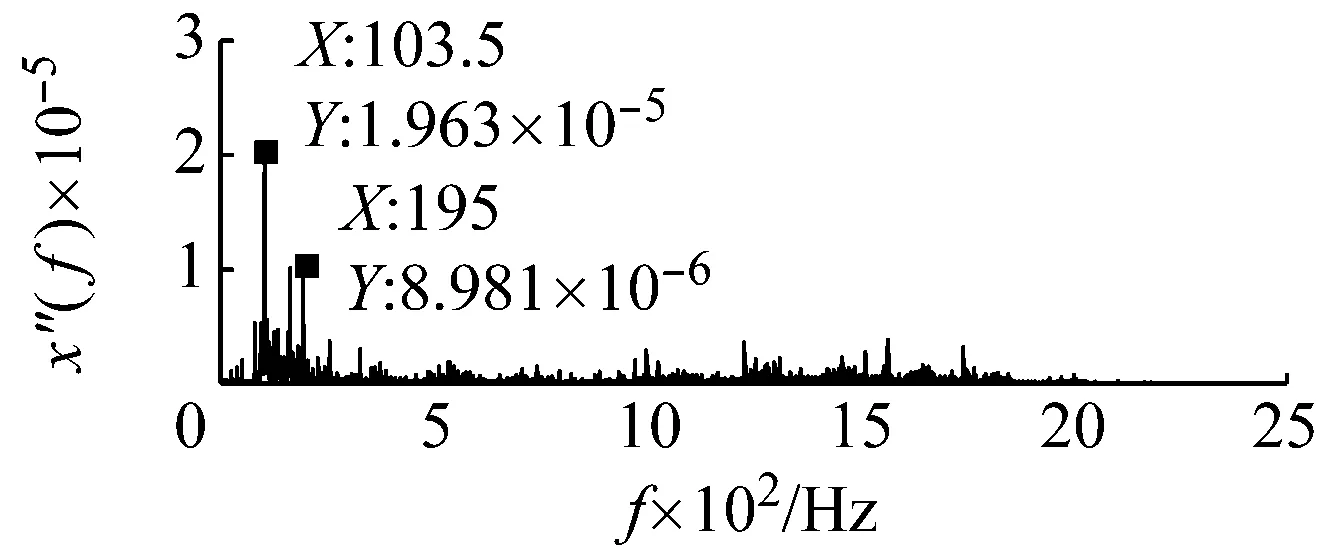
(b)

而系統參數a或b的調節都會引起勢函數特征(勢壘高度和勢阱間距)的變化，因此不便于直觀地了解PFCPs的變化對SR的影響。

(1) 通過PFCPs的引入，提出了基于勢壘高度h和勢阱間距w調節的SR方法。依照Kramers逃逸速率與目標信號頻率的匹配關系，以系統輸出信噪比為評價指標，通過調節勢壘高度參數h，得到最優的參數對(h，w)，使系統輸出響應達到最佳值。

(2) 為了克服采樣頻比對傳統SR的限制，本文給出了基于濾波器技術的時域換頻方法，實現了低采樣頻比的信號檢測。動車轉向架軸承內圈、外圈以及滾動體故障實驗檢測研究表明，采用換頻技術和PFCPs調節的SR信號檢測方法，可以對噪聲干擾中的故障信號進行有效檢測，驗證了本文所提出方法的可行性與有效性。