關節軸承錐曲面模具冷擠壓裝配時外圈的成形仿真與分析

孫屹博，于波，吳國雄

(1.大連交通大學 機車車輛工程學院，遼寧 大連 116028；2.蘇州東菱振動試驗儀器有限公司，江蘇 蘇州 215011)

關節軸承具有結構簡單緊湊,體積小,耐沖擊,可靠性高等特點，可承受徑向載荷、軸向載荷或徑向、軸向同時作用的聯合載荷，在外載荷作用下可實現擺動和一定角度范圍的傾斜運動，廣泛應用在礦山機械、重載運輸、水利航海和軍工機械等領域[1-4]。目前關節軸承擠壓成形裝配工藝中主要存在外圈受壓過度，導致其內表面出現褶皺即壓潰現象，或由于收口能力不足導致的內外圈間隙不均，其中，擠壓模具結構是影響關節軸承成形質量的主要因素。

針對關節軸承冷擠壓成形裝配，國內外學者從軸承擠壓方式、工藝參數和外圈形狀等方面進行了廣泛的研究。文獻[5]采用雙模具成形工藝避免單向成形造成的缺陷，通過優化軸承外圈的形狀大大降低擠壓成形過程中的擠壓力；文獻[6]基于球坐標下和金屬塑性變形公式分析棒體擠壓，得出最佳模角與擠壓變形程度之間的關系；文獻[7]提出了一種關節軸承外圈的軋制工藝以及加工流程，并對模具進行了優化；文獻[8]通過優化模具結構及軸承外圈形狀，改善內外圈間隙分布不均及內外圈金屬流動速度分布不均的問題；文獻[9]通過虛擬正交試驗的方法對關節軸承的工藝參數進行優化設計，使關節軸承擠壓成形達到預期值。

為解決關節軸承在成形裝配過程中外圈壓潰和收口能力不足的問題，提出了一種具有錐曲面模腔的擠壓模具，并利用錐曲面模具開展了關節軸承擠壓成形過程的有限元分析，對外圈在不同模具結構作用下的包角、內球面半徑和擠壓力與進給位移之間的關系進行了研究。

1 關節軸承擠壓成形裝配原理

內圈無作用力模壓成形工藝是關節軸承成形裝配中較常見的工藝方法，具有高效率，高精度，便于控制等特點，該工藝成形原理如圖1所示。

1—擠壓上模；2—軸承外圈；3—軸承內圈；4—擠壓下模

擠壓成形裝配過程中,外圈毛坯的內表面直徑大于內圈球面直徑，即內外圈之間留有一定間隙。內外圈相互裝配，且放置于上下模具之間，上下模具的腔體部分與外圈外表面相接觸，如圖1a所示。上下模具在擠壓力的作用下開始做相向運動，外圈受到擠壓模具的擠壓作用發生塑性變形，內外圈的間隙逐漸減小，外圈內表面也逐漸變為球面，如圖1b所示。內外圈呈球面配合，模具停止進給，最后撤走擠壓模具，關節軸承擠壓成形裝配完成，如圖1c所示[10]。擠壓成形裝配過程中，外圈僅在擠壓模具的作用下發生變形，外圈與內圈間無抱死和擠壓作用，有效保護了內外圈接觸面的表面質量。

擠壓成形裝配過程中，外圈始終貼合模具腔體表面而逐漸變形。曲面模具(圖2a)的內部腔體為曲面結構，其半徑為r1[11]；錐面模具(圖2b)的腔體為錐面，其錐角為θ[12]；錐曲面模具(圖2c)是在前2種模具結構的基礎上研究出的一種新型模具，模具腔體呈錐面和曲面組合結構，為使外圈在擠壓過程平滑進入模腔深處，模具的錐面和曲面相切配合。為方便研究，后文稱曲面模具為模具a，錐面模具為模具b，錐曲面模具為模具c。

圖2 關節軸承的3種擠壓模具

2 關節軸承擠壓成形裝配建模

AS14104-D系列關節軸承的結構尺寸近似呈倍率分布，為研究方便,選取AS14104-D系列中尺寸最小的MS14104-3型軸承,建立關節軸承擠壓成形裝配的有限元模型，對軸承擠壓成形過程進行有限元仿真分析[13]。AS14104-D系列關節軸承的結構如圖3所示，r為外圈內球面半徑；α為外圈包角，通過計算得該系列關節軸承成形后的包角α約為60°。

圖3 AS14104-D系列關節軸承結構示意圖

基于軸承內圈無作用力模壓成形原理，對關節軸承擠壓成形裝配過程進行仿真分析，擠壓成形裝配過程中內圈對外圈變形無壓力作用，因此，在仿真過程中只對外圈進行仿真分析。

關節軸承結構和擠壓成形裝配裝置結構均為回轉體，在擠壓成形裝配過程中軸承的幾何變化和受力情況均是對稱分布，所以，利用二維軸對稱有限元模型進行仿真分析。考慮到擠壓模具受力變形影響外圈成形結果，將擠壓模具設為解析剛體單元。外圈在擠壓過程中塑性變形較大，在計算中需考慮結構的幾何非線性問題，采用CAX4R四結點雙線性軸對稱四邊形單元，為提高計算精度和滿足對外圈成形表征分析的要求，只對關節軸承外圈的1/4進行擠壓仿真分析。關節軸承擠壓成形裝配仿真分析的有限元模型如圖4所示[7]。根據關節軸承實際擠壓條件設定套圈材料仿真參數，具體參數值見表1。

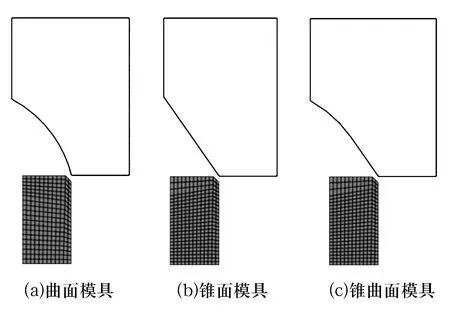
圖4 關節軸承擠壓成形裝配的有限元模型

表1 關節軸承有限元仿真分析套圈材料參數

關節軸承擠壓成形裝配的有限元模型為二維軸對稱模型，對模型的邊界條件設定時僅對R(水平)方向和Z(豎直)方向進行約束，其他方向不必考慮。軸承擠壓成形裝配過程中，外圈的外表面與擠壓模具模腔的內表面接觸，外圈中部主要的變形沿著R方向平移，因此對外圈Z方向進行約束，擠壓模具對R方向約束，其邊界條件如圖5所示[14]。由于模具的剛度大于外圈，設定模具為主接觸面，外圈外表面為副接觸面，接觸面摩擦理論采用庫侖摩擦定律，摩擦因數為0.05。仿真過程中通過幅值控制模具各時刻的進給位移量，實現對外圈回彈前后變形特性的采集。

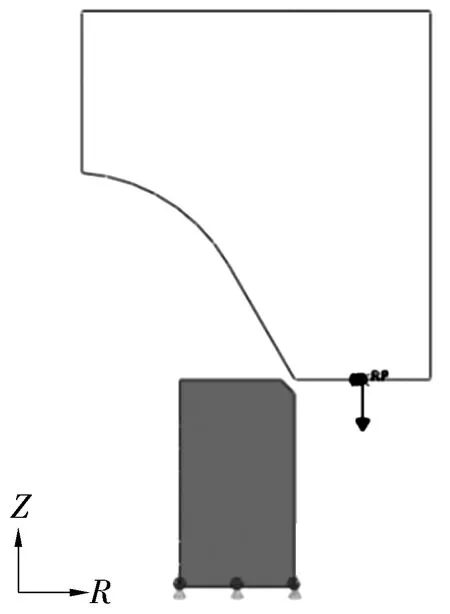
圖5 關節軸承擠壓成形裝配的有限元模型邊界條件

3 仿真結果分析

因錐面模具對軸承外圈壓潰作用最明顯，以錐面模具擠壓過程為例，外圈的Von Mises等效應力分布如圖6所示。外圈與模具接觸處的應力較大，隨模具的下壓，接觸處的應力逐漸增大。擠壓過程中關節軸承外圈的內表面呈受壓狀態，外表面呈拉伸狀態，隨著模具的不斷下壓外圈由平面變為弧面，內圈弧面的成形半徑rf逐漸減小，成形包角αf逐漸增大，即rf1>rf2，αf1<αf2，如圖6a和圖6b所示。當外圈的變形達到軸承的標準要求，撤走擠壓模具，外圈開始自由回彈，回彈后的內球面半徑為re,回彈后包角為αe,回彈后軸承外圈的應力主要集中于外圈外表面邊緣的兩頂角處，如圖6c所示。若模具的進給位移大于軸承變形所需要的極限位移量，外圈內表面會在中部出現褶皺，如圖6d所示。

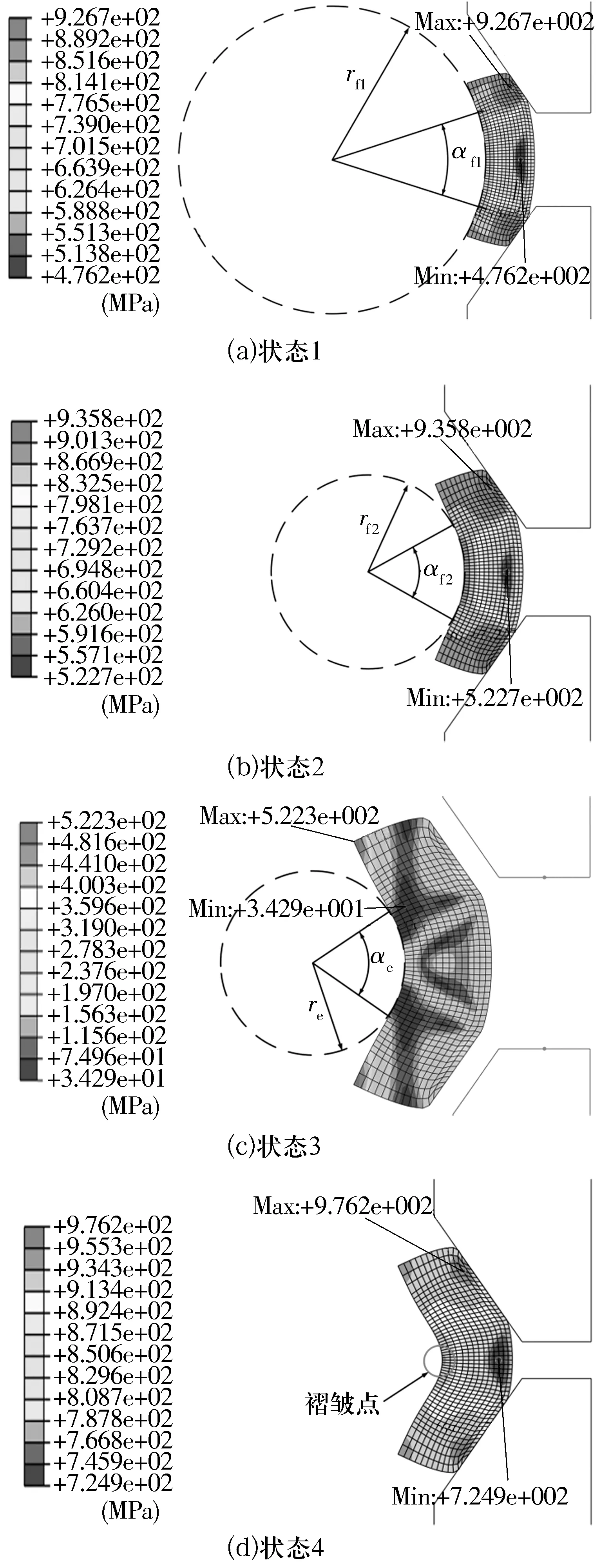
圖6 擠壓過程關節軸承外圈形變狀態云圖

擠壓成形裝配過程中,外圈的成形包角變化曲線如圖7所示,從圖中可以看出，軸承外圈包角在卸載前后的變化趨勢相同，但經過回彈后的外圈包角有所減小。模具a作用下，外圈包角在擠壓前期速率增長較慢，隨模具進給位移的增大，擠壓后期包角成形速率逐步增大；模具b作用下,外圈包角先以較大速率增大，到達b1點后逐漸減小，此時外圈開始出現壓潰；模具c作用下,外圈包角在擠壓前期與模具b作用下的變化相似，前期成形速率增長較快，到達一定值后以較平緩的變化趨勢繼續增大，整個過程模具c對應的包角值大于模具a，b，且無減小趨勢，即擠壓過程無壓潰。

圖7 關節軸承擠壓成形過程模具位移-外圈包角變化曲線

標準要求軸承成形后外圈包角約為60°，因此，加工成形過程中αe必須大于60°才可滿足軸承工況要求。由圖7b可知，模具c作用下的αe最先超過60°，此時模具進給位移為2.90 mm，模具b作用下的αe達到60°對應的進給位移為3.15 mm，模具a作用下的αe未能達到60°要求。同等模具位移(4 mm)情況下，模具c對軸承外圈的作用效率及對外圈的收口能力優于其他2種模具，而且外圈未出現壓潰現象，可有效保證軸承的裝配質量。

隨著擠壓模具進給量的不斷增加，α時刻發生變化，r也發生變化，如圖8所示。從圖中可以看出，r隨擠壓模具進給位移的增大而逐漸減小，模具a作用下r始終大于模具b，c作用下，在相同模具進給區間，模具a作用下r的前后波動最大，即前期以較大的速率減小，后期減小速率逐漸平緩，模具b，c作用下r均呈平緩分布。根據MS14104-3型關節軸承標準尺寸要求，成形后內球面半徑為5.17 mm，因此軸承在加工過程中re要小于5.17 mm才可達到軸承的裝配要求。由圖8b可知,模具c作用下re最先達到5.17 mm，對應的模具進給位移為2.8 mm，模具a,b滿足re為5.17 mm的位移分別為3.6和3.2 mm。

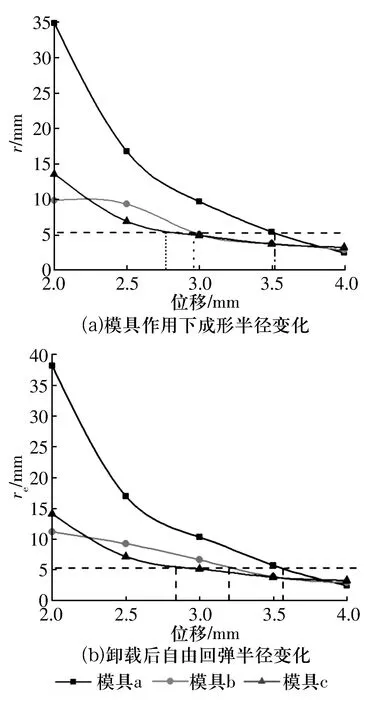
圖8 關節軸承擠壓成形過程模具位移-外圈內球面半徑變化曲線

上述滿足關節軸承外圈形變標準要求的模具位移區間統計結果見表2。表中模具a因在同等位移作用下的αe未達到標準要求，因此不作為統計范圍;模具b的有效作用區間遠小于模具c，說明模具b的有效作用時間較短，實際生產中對模具進給位移的控制精度要求較高;模具c的有效作用區間大于其他模具，即在生產過程中便于控制模具c的進給位移，同時,模具c有效區間的初始值最小，說明模具c作用下的外圈形變效率高于其他2種模具。

表2 外圈形變標準所需的模具位移區間

擠壓成形裝配過程中，壓力機為外圈成形提供擠壓力，軸承變形所需擠壓力的大小受擠壓模具的結構影響。軸承擠壓成形過程中壓力機的擠壓力曲線如圖9所示，c，b1，b2對應表2中模具c有效擠壓區間的起始值和模具b的有效區間的始末值。從圖中可以看出，隨模具進給位移的逐漸增大，外圈變形所需的擠壓力也逐漸增大，模具c在同等位移下的擠壓力始終大于模具a，b對應的擠壓力，其中模具a的擠壓力小于模具b的擠壓力。

圖9 關節軸承擠壓成形過程模具位移-擠壓力曲線

4 結束語

針對關節軸承冷擠壓成形裝配過程中外圈受模具作用下出現的壓潰和收口不足等問題,提出了一種具有錐曲面模腔的擠壓模具，并對外圈成形過程進行有限元分析。計算得到外圈在錐曲面模具、曲面模具、錐面模具3種模具作用下的包角、內球面半徑和擠壓力的變化特征，對比分析同等模具位移區間下外圈形變特點以及形變所需擠壓力的大小，同等外圈形變程度下各模具所需的進給位移量。結果表明：同等模具進給位移區間，錐曲面作用下的外圈變形未出現壓潰現象，可有效提高外圈的成形質量，運用錐曲面模具的成形效率以及對外圈的收口能力高于其他2種模具；同等形變要求下錐曲面模具所需要的擠壓力小于其他2種模具。