履帶式全方位移動平臺的運動學分析與仿真*

張豫南，房 遠，楊懷彬，崔 智，史浩楠

（陸軍裝甲兵學院，北京 100072）

0 引言

全方位移動平臺能夠實現前后平移、左右平移和繞自身旋轉3個自由度的運動，這種運動學上的優勢使其在狹窄空間作業的機器人運動系統得到廣泛應用，并成為機器人移動機構的一個主要發展趨勢［1］。全方位移動平臺種類多樣，其中以Mecanum輪式移動平臺的研究和應用最為成熟［2］。Mecanum輪式移動平臺采用與普通轎車相似的布局形式，可擴展性強，與其他全方位移動平臺相比具有較強的承載能力，而且平臺的相關控制技術成熟，故得到了較為廣泛的應用，例如物流倉儲中使用的Mecanum輪式叉車。由于Mecanum輪自身的結構特點，使得輥子軸向受力大、易磨損，且在輪子正常運動時輥子一般伴隨有滑動［3］，無法準確完成直線運動。Mecanum輪式移動平臺在運動過程中振動大，越野、越障能力差，在地面濕滑的情況下，運動能力差。

為了改善Mecanum輪式移動平臺的運動能力，一種思路是直接對Mecanum輪進行改進，包括設計橢圓形的 Mecanum 輪［4］，增加輥子鎖緊機構［5］，對輥子厚度補償［6］等，增加了輪的復雜程度，其加工成本和難度也較高，實際效果不好。另一種思路是受Mecanum輪式移動平臺的啟發，設計出履帶式全方位移動平臺，矩形布局的履帶式全方位移動平臺如圖1所示，其行走機構的細節部分如圖2所示。履帶式全方位移動平臺的實用性強，應用領域廣泛，既能實現全方位運動，又具有傳統履帶式移動平臺的優點，如：運動平穩；接地面加大，載重能力強；越野能力強；具有一定的柔性，對不平路面具有一定的“濾波”作用等［7］。

圖1 矩形布局的履帶式全方位移動平臺

圖2 履帶式全方位移動平臺行走機構

目前針對履帶式全方位移動平臺的研究很少，現有文獻中的運動學方程和動力學方程的推導過程復雜，推導結果的通用性不強，并且只對矩形布局的履帶式全方位移動平臺進行了驗證，限制了對履帶式移動平臺運動特性的進一步研究。本文針對履帶式移動平臺的運動學方程，提出一種較為簡便的推導方法，并以三角形布局的履帶式移動平臺為例，對運動學方程進行仿真驗證。

1 運動學方程

本文在運動學方程推導的過程中進行了簡化，并不直接針對履帶式全方位移動平臺進行推導，而是針對在運動學方程上等效的圓柱輥子Mecanum輪全方位移動平臺（以下簡稱“圓柱輥子全方位移動平臺”）進行推導，圓柱輥子全方位輪和圓柱輥子全方位移動平臺如圖3、圖4和圖6所示。對比可知，履帶式全方位移動平臺和圓柱輥子全方位移動平臺的區別在于是否有履帶和圓柱輥子（履帶上是圓柱小輪）數量的多少，如果假設履帶式全方位移動平臺的履帶接地段的滑轉、滑移為零，圓柱輥子全方位移動平臺的輥子不發生滑移，那么二者的運動學方程將是完全相同的。

1.1 圓柱輥子全方位移動平臺運動學建模

在本文中對全方位移動平臺的運動過程作出如下假設：

1）平臺車體、全方位輪和地面均為剛體，平臺在理想的平面上運動；

2）輥子與地面之間具有足夠大的摩擦力，輥子不發生滑移；

3）平臺的重心在其平面幾何中心上；

4）假定輥子與地面的接觸點在全方位輪正下方，忽略圓柱輥子全方位輪轉動過程中輥子與地面接觸點的變化。

采用矢量分析法，圓柱輥子全方位移動平臺的運動學方程推導過程如圖3所示：

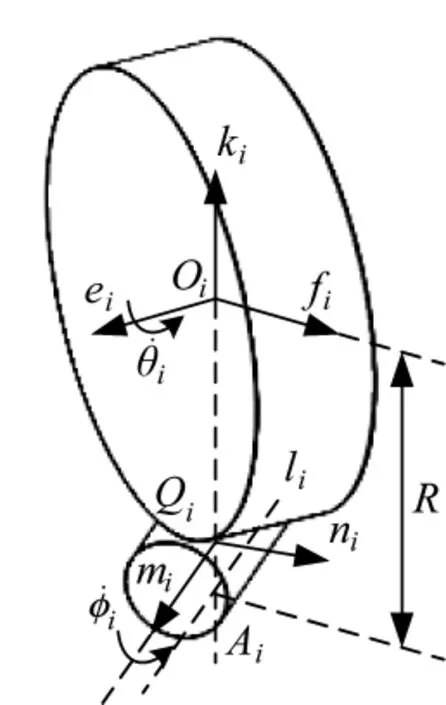
圖3 觸地圓柱輥子示意圖

圖4 輪相對平臺質心示意圖

對于由n個圓柱輥子全方位輪構成的移動平臺，首先討論第i個圓柱輥子全方位輪的速度表達式，圖3所示為基于圓柱輥子全方位輪坐標系內各量的定義，圖4所示為基于圓柱輥子全方位移動平臺坐標系內各量的定義。定義輪轂轉過的角度為θi，輪轂轉速為θ觶i，圓柱輥子轉過的角度為，圓柱輥子的轉速為，點Qi為圓柱輥子的中心點，點Oi為輪轂的中心點，點Oi的速度向量為o觶i，全方位輪和地面的接觸線為圓柱輥子上的線li，過點Oi和Qi的直線和 li相交于點 Ai，點 Ai的速度向量為a觶i。定義 ω 為平臺車體轉動角速度，定義點B為平臺幾何中心，b觶為平臺的速度向量，定義di為從B點指向Oi點的向量，ei為沿輪轂軸線方向的單位向量，ki為沿OiQi方向的單位向量，fi為過點Oi且垂直于ei和ki的單位向量，mi為沿圓柱輥子軸線方向的單位向量，ni為過點Oi且垂直于mi和ki的單位向量，R為全方位輪半徑，r為圓柱棍子半徑。

將Oi點的速度與Ai點的速度聯系起來，有

其中，vi為Oi相對于Qi的速度。

記ωR為輪轂角速度，ωr為輥子角速度，則有

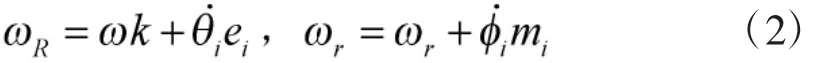
從線速度的角度有

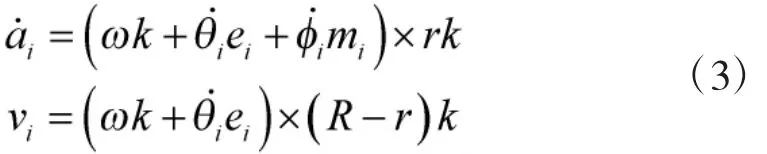
也即有

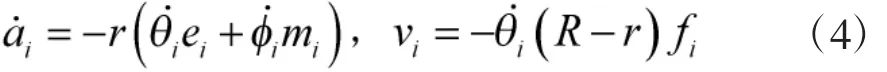
將式（4）代入式（1）得

下面討論Oi相對于B點的速度表達式，如圖4所示，有

據圖4中矢量之間的關系有

將式（5）兩邊同時點乘 mi，并將式（7）代入可得，

將式（6）兩邊同時點乘 gi，可得

聯立式（8）和式（9），可得θ觶i和 ω 與b觶的關系為

考慮n個圓柱輥子全方位輪的運動方程，則平臺的逆運動學方程為

相應的，平臺的正向運動學方程為

平臺能實現全方位運動的必要條件是系統的速度逆雅可比矩陣滿秩，即rank（K）=3，此時系統不存在奇異位形。

1.2 矩形布局的履帶式全方位移動平臺運動學方程

應用式（11）和式（12），對如下頁圖 5所示的矩形布局的履帶式全方位移動平臺進行運動學分析，圖中履帶上的小輥子用直線段代替。根據1.1的內容，首先將矩形布局的履帶式全方位移動平臺等效成矩形布局的圓柱輥子全方位移動平臺，對其進行運動學分析，如圖6所示。圖5和圖6均為俯視圖。圖6中表示平臺的廣義速度，表示4個輪子的轉速，方向符合右手定則，L和l分別表示前后輪之間距離的一半和左右輪之間距離的一半，圓柱輥子與輪軸的夾角分別取45°和-45°。根據式（11）和式（12）可以得到圓柱輥子全方位移動平臺的正向運動學方程為

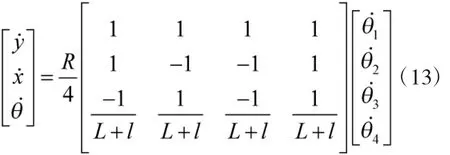
圖5 矩形布局的履帶式全方位移動平臺結構圖

圖6 矩形布局的圓柱輥子全方位移動平臺

逆向運動學方程為

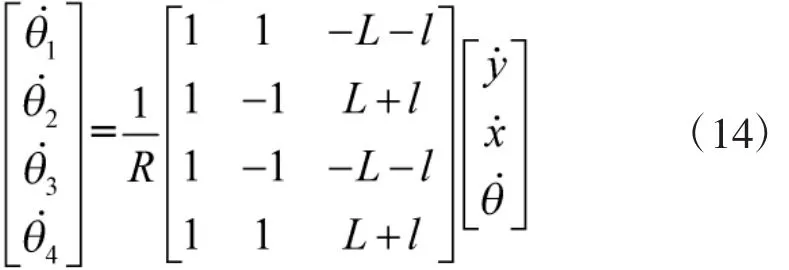
由前文1.1的分析可知，經過等效分析得到的式（13）即為履帶式全方位移動平臺的正向運動學方程，式（14）即為履帶式全方位移動平臺的逆向運動學方程。此結論與文獻［7-8］的分析結果一致，并且已經過圖1和圖5所示的履帶式全方位移動平臺進行過實車驗證，故可知本文運動學分析方法的正確性。

2 分析與仿真

在1.1節運動學方程的推導過程中，將全方位履帶等效成圓柱輥子全方位輪處理，本質上是作出假設，認為履帶式全方位移動平臺的運動學特性和履帶長度無關。為了證明該等效處理的正確性，同時驗證本文公式結論的正確性，在Adams中建立車體相同，履帶長度不同的履帶式三角形全方位移動平臺模型，進行中心轉向仿真驗證。三角形車體為等邊三角形，三條履帶呈中心對稱分布。

2.1 履帶式三角形車體全方位移動平臺運動學建模

對履帶式三角形車體全方位移動平臺進行運動學分析，如圖7所示。

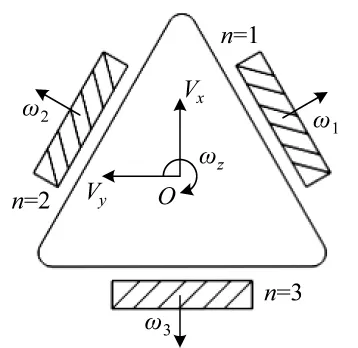
圖7 履帶式三角形車體全方位移動平臺結構示意圖

圖7 為俯視圖，圖中按逆時針方向對3條履帶進行了從 1到 3的編號，ω1，ω2，ω3分別表示 3條履帶的轉動角速度，方向符合右手定則，VyOVx為車體坐標系，ωz為車體中心轉向角速度，圓柱輥子與輪軸的夾角均為45°。設三角形車體中心點O到履帶對稱中心線的垂直距離為l，履帶的主動輪半徑為R，那么根據1.1的分析過程和式（11）可以得到履帶式三角形全方位移動平臺的逆運動學方程為

由式（15）可知，雅可比矩陣的秩有 rank（K）=3，滿足全方位運動的條件，故履帶式三角形全方位移動平臺能夠進行全方位運動。

根據式（12）和式（15）可知平臺的中心轉向角速度表達式為

2.2 履帶式三角形車體全方位移動平臺仿真與分析

3種平臺的Adams模型如下頁圖8所示，測量可得l=0.685 m，R=0.112 m。為了方便將仿真結果進行對比，設定ωz=1 rad/s，假設每個平臺3條履帶的角速度都相等，則根據式（16）有 ω1=ω2=ω3=6.116 1 rad/s。

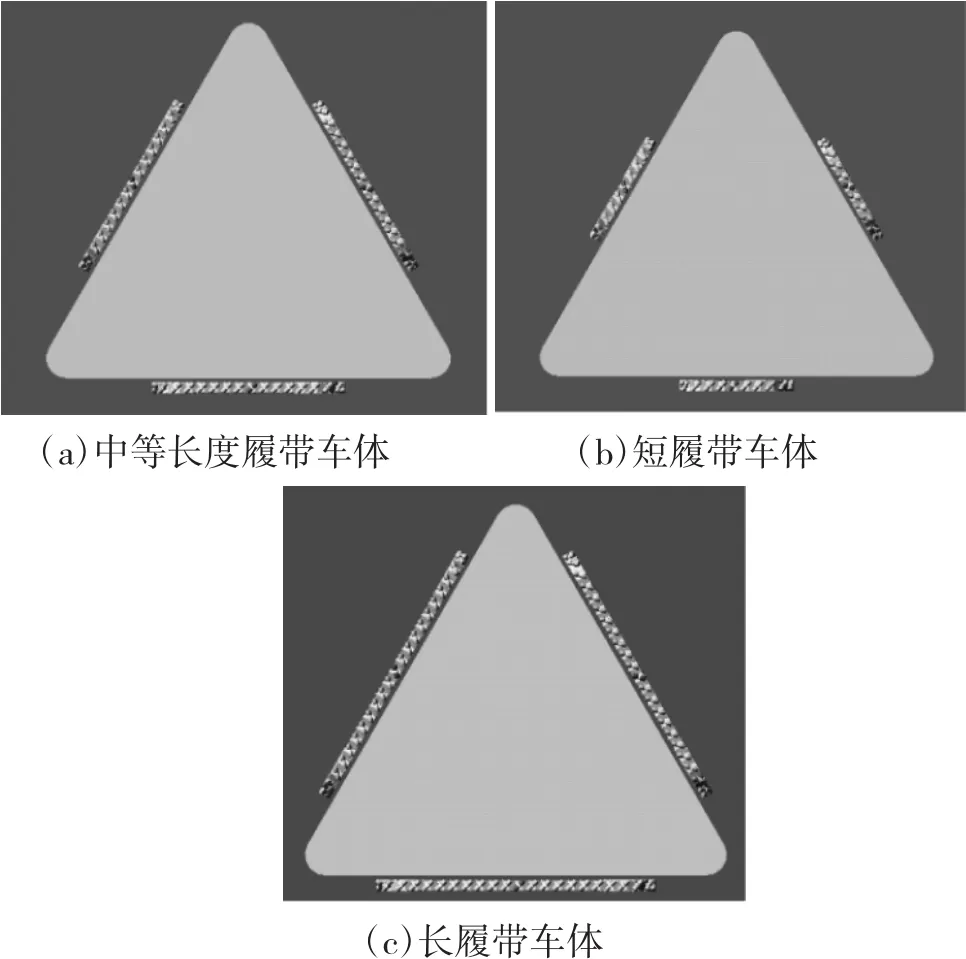
圖8 3種平臺的Adams模型

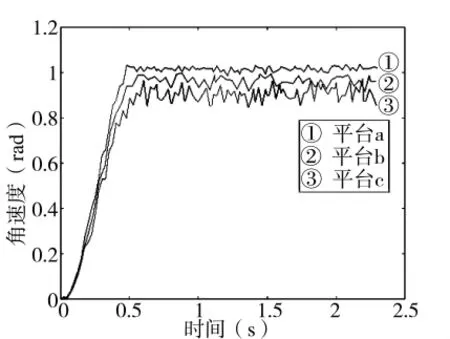
圖9 3種平臺的中心轉向角速度值平均值

3種平臺經仿真驗證均能實現平面上的全方位運動，主動輪的速度輸入均為 STEP（TIME，0，0，0.5，6.116 1），參數和仿真結果對比見表 1，其中的中心轉向角速度平均值是取0.5 s之后的中心轉向角速度值求均值得出，仿真結果如圖9所示。由表1和圖9可知，3種平臺的中心轉向角速度誤差都在10%以內，證明了相關公式結論和運動學方程的正確性。

表1 3種平臺的參數和仿真結果

由表1和圖9還可以看出，履帶式三角形全方位移動平臺的中心轉向角速度平均絕對誤差，隨著履帶接地長度的增加而增加，這是因為履帶接地長度越長，與地面接觸的小輥子的打滑積累越嚴重的緣故［9］。

3 結論

本文提出一種簡便的履帶式全方位移動平臺的運動學推導方法，在滿足1.1中4條假設的前提下，推導過程中將履帶式全方位移動平臺用圓柱輥子全方位移動平臺代替。將此方法應用于矩形布局的履帶式全方位移動平臺，得出的運動學方程與現有文獻的結論完全一致，并且已經過實車驗證。將此方法應用于履帶式三角形車體全方位移動平臺的運動學分析，在Adams中建立3種履帶長度不同的履帶式三角形車體全方位移動平臺，進行中心轉向角速度對比仿真，得到3種平臺的中心轉向角速度平均絕對誤差均在10%以內，證明該方法的正確性。