未知量測噪聲分布下的CBMeMBer算法

胡建旺 ，董 青 ，張 鐵 ，吉 兵

（1.陸軍工程大學(xué)石家莊校區(qū)，石家莊 050003；2.北方聯(lián)創(chuàng)通信有限公司，南昌 330000）

0 引言

近年來，基于隨機(jī)有限集（Random Finite Set，RFS）［1］的目標(biāo)跟蹤技術(shù)發(fā)展迅速［2-4］。2008 年 Mahler提出了基于多伯努利隨機(jī)集的多目標(biāo)多伯努利（Multi-Target Multi-Bernoulli，MeMBer）跟蹤算法［5］。針對MeMBer會高估目標(biāo)數(shù)目的問題，Vo提出了勢均衡多目標(biāo)多伯努利（Cardinality Balanced MeMBer，CBMeMBer）濾波算法［6］。在目標(biāo)跟蹤過程中，由于電磁環(huán)境、溫度和其他因素影響，量測噪聲概率分布難以準(zhǔn)確獲取。針對此問題，部分學(xué)者基于隨機(jī)集理論，對該問題進(jìn)行了一定的研究［7-10］。

本文針對未知量測噪聲分布下的目標(biāo)跟蹤問題，引入代價參考粒子濾波（Cast Reference Particle Filter，CRPF）［11-13］思想，提出一種基于風(fēng)險評估的CBMeMBer 算 法 （Risk Evaluation CBMeMBer，RE-CBMeMBer）。算法引入風(fēng)險函數(shù)計(jì)算CBMeMBer粒子風(fēng)險值，之后對粒子風(fēng)險值進(jìn)行評估，用評估結(jié)果替代似然函數(shù)，以此實(shí)現(xiàn)粒子的權(quán)值更新。仿真結(jié)果表明，本文所提算法在運(yùn)行速率，穩(wěn)定性上都優(yōu)于SMC-CBMeMBer算法。

1 SMC-CBMeMBer濾波器

根據(jù)k時刻的后驗(yàn)多目標(biāo)密度表達(dá)式可知，CBMeMBer算法的核心思想是遞推包含存在概率和后驗(yàn)概率密度的多個集合。采用粒子實(shí)現(xiàn)形式時，SMCCBMeMBer算法傳遞包含權(quán)重和粒子的集合，每個集合表示1條假設(shè)軌跡。假設(shè)k-1時刻的CBMeMBer近似為一族帶權(quán)粒子

1.1 預(yù)測

則預(yù)測項(xiàng)分別為：

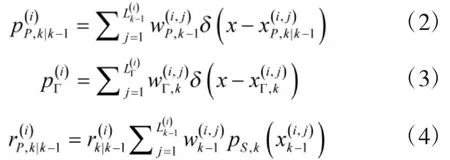
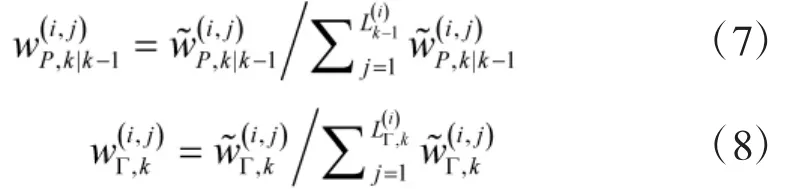
1.2 更新

假定k時刻預(yù)測的多目標(biāo)密度為：

則更新項(xiàng)分別為：

其中

2 未知量測噪聲分布下的粒子CBMeMBer算法

根據(jù)式（21）可知，標(biāo)準(zhǔn) SMC-CBMeMBer算法必須在多維量測空間中計(jì)算似然函數(shù)。然而該操作存在兩點(diǎn)不足：一是針對未知復(fù)雜的量測噪聲，其概率分布通常難以獲取，而概率分布不準(zhǔn)確將嚴(yán)重影響算法性能；二是多維量測空間中進(jìn)行似然函數(shù)計(jì)算需要消耗較多的計(jì)算時間。而解決這些問題的途徑之一是避開似然函數(shù)計(jì)算。

2.1 風(fēng)險函數(shù)與評估函數(shù)

首先經(jīng)風(fēng)險函數(shù)表達(dá)式（22）計(jì)算，當(dāng)粒子與量測值距離較近時，賦予該粒子較小的風(fēng)險值，反之，則賦予較大風(fēng)險值。

為驗(yàn)證指數(shù)函數(shù)作為粒子質(zhì)量評估函數(shù)的有效性，采用式（24）對似然函數(shù)和評估函數(shù)對粒子分辨能力進(jìn)行對比。式中，σ（0，ε）表示以 0為中心，半徑為 ε 的鄰域，ε表示評估函數(shù)與似然函數(shù)對粒子分辨能力的接近程度。實(shí)驗(yàn)得出，在量測噪聲分布為N（0，1），=1時，風(fēng)險評估函數(shù)與似然函數(shù)對粒子的分辨能力差別為ε=0.002 5，分辨能力相當(dāng)。

此外，由于真實(shí)場景下，噪聲環(huán)境并非固定不變，因此，評估函數(shù)參數(shù)的取值也應(yīng)不同。目前理論推導(dǎo)參數(shù)的取值比較困難，只能根據(jù)經(jīng)驗(yàn)確定的取值區(qū)間。實(shí)驗(yàn)結(jié)果表明，在不同的量測噪聲環(huán)境中，參數(shù)的取值與噪聲大小成反比。參數(shù)的經(jīng)驗(yàn)取值區(qū)間為：噪聲較小時，∈［1.2，1.4］；噪聲適中時∈［0.9，1.1］；噪聲較大時，∈［0.6，0.8］。

從原理上看，風(fēng)險評估函數(shù)的作用等同于似然函數(shù)，即都是用來評估粒子質(zhì)量，但風(fēng)險評估函數(shù)不需要知道量測噪聲分布情況，只需在一維量測空間中計(jì)算新息范數(shù)和指數(shù)函數(shù)，一定程度上克服了狀態(tài)估計(jì)對粒子的依賴。

2.2 RE-CBMeMBer濾波算法

1）預(yù)測

根據(jù)重要性采樣函數(shù)抽取粒子并進(jìn)行粒子預(yù)測，并通過式（5）~式（8）計(jì)算粒子權(quán)值得到

2）風(fēng)險計(jì)算和評估

利用式（22）計(jì)算粒子風(fēng)險值，并將粒子風(fēng)險值代入式（23）對粒子風(fēng)險進(jìn)行評估。

3）粒子更新

利用式（17）、式（18）分別計(jì)算漏檢和量測更新的目標(biāo)的粒子權(quán)值，并進(jìn)行歸一化處理；利用式（11）、式（13）計(jì)算假設(shè)軌跡的存在概率，得到更新的多伯努利隨機(jī)集為

4）軌跡修剪、重采樣和狀態(tài)提取。

3 仿真實(shí)驗(yàn)

3.1 仿真參數(shù)設(shè)置

本文仿真場景設(shè)置為：仿真時間為80 s；仿真步長為 1 s；觀測區(qū)域?yàn)?x-y二維平面區(qū)域［-2π，2π］*［0，2 000 m］。先后出現(xiàn)6個做轉(zhuǎn)彎運(yùn)動（CT）的目標(biāo)。狀態(tài)方程和量測方程分別為：

3.2 算法性能分析

本仿真中目標(biāo)的真實(shí)軌跡如圖1所示，其中圓圈○表示目標(biāo)軌跡起點(diǎn)，三角形△表示目標(biāo)軌跡終結(jié)。

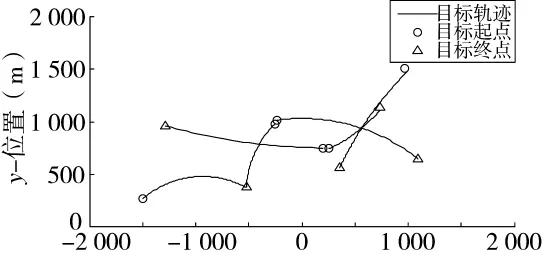
圖1 目標(biāo)實(shí)際軌跡圖

1）仿真實(shí)驗(yàn)1：量測噪聲先驗(yàn)已知，且為高斯分布

當(dāng)量測噪聲為高斯分布且分布已知。假設(shè)量測噪聲實(shí)際概率分布為 wk~N（0，R0），其中

仿真實(shí)驗(yàn)1中，假設(shè)SMC-CBMeMBer算法掌握的量測噪聲概率分布為N（0，R），其中R=R0。圖2給出了SMC-CBMeMBer算法和改進(jìn)算法的跟蹤軌跡圖。從圖2可以看出，在量測噪聲先驗(yàn)已知的情況下，SMC-CBMeMBer和RE-CBMeMBer算法都能較為精確地跟蹤到所有目標(biāo)，且跟蹤精度相差不大。

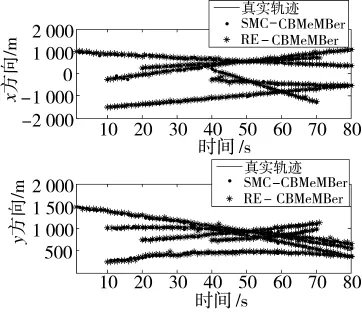
圖2 仿真實(shí)驗(yàn)1的多目標(biāo)跟蹤軌跡圖

圖3 仿真實(shí)驗(yàn)1的目標(biāo)數(shù)目估計(jì)

圖3 表示真實(shí)目標(biāo)數(shù)目和兩種跟蹤算法對目標(biāo)數(shù)目估計(jì)結(jié)果。可知當(dāng)量測噪聲先驗(yàn)分布與真實(shí)分布匹配時，兩種算法對目標(biāo)數(shù)目的估計(jì)能力相當(dāng)。

為充分比較兩種算法的跟蹤性能，本仿真實(shí)驗(yàn)采用OSPA距離來評定兩種算法的跟蹤誤差。由圖4可知，兩種算法誤差距離相當(dāng)。由于算法具有隨機(jī)性，單次濾波結(jié)果具有差異性，因此，通過100次蒙特卡洛仿真，從統(tǒng)計(jì)意義上比較算法平均運(yùn)行時間t和平均OSPA距離d。

圖4 OSPA距離

表1 兩種算法平均運(yùn)行時間和OSPA距離比較

由表1可知，兩種算法跟蹤精度相當(dāng)，但由于RE-CBMeMBer算法在粒子更新時，避開多維空間中似然函數(shù)的求解，RE-CBMeMBer的運(yùn)行時間近似為SMC-CBMeMBer運(yùn)行時間的。

2）仿真實(shí)驗(yàn)2：量測噪聲先驗(yàn)未知，且為伽馬分布

由于真實(shí)環(huán)境下噪聲分布常為非高斯形式，因此，仿真實(shí)驗(yàn)2在非高斯量測噪聲環(huán)境下對SMC-CBMeMBer和RE-CBMeMBer算法性能進(jìn)行比較。假設(shè)實(shí)際量測噪聲分布為伽馬分布：。假設(shè)SMC-CBMeMBer算法獲得的量測噪聲的先驗(yàn)分布為N（0，R1），其中，R1=diag（0.1，0.5）。

下頁圖5為多目標(biāo)跟蹤軌跡圖，可知SMC-CBMeMBer算法僅在前幾個時刻跟蹤到目標(biāo)，這是由于量測噪聲的先驗(yàn)分布與實(shí)際分布不匹配，誤差迅速累積，導(dǎo)致目標(biāo)丟失。相比而言，RE-CBMeMBer算法能較好地跟蹤目標(biāo)，具有較好的穩(wěn)定性和魯棒性。

圖5 仿真實(shí)驗(yàn)2的多目標(biāo)跟蹤軌跡圖

從圖6可知，SMC-CBMeMBer濾波算法僅在前6個時刻準(zhǔn)確估計(jì)到目標(biāo)數(shù)目，其余時刻均產(chǎn)生錯誤估計(jì)，而RE-CBMeMBer濾波算法除個別時刻估計(jì)錯誤之外，大部分時刻均做到準(zhǔn)確估計(jì)目標(biāo)數(shù)目。經(jīng)過50次蒙特卡洛仿真，采用多次仿真中算法的發(fā)散次數(shù)來衡量算法穩(wěn)定性，結(jié)果顯示，SMC-CBMeMBer濾波算法總共發(fā)散 36次，而RE-CBMeMBer濾波算法未發(fā)散。

圖6 仿真實(shí)驗(yàn)2的目標(biāo)數(shù)目估計(jì)

實(shí)驗(yàn)結(jié)果表明：當(dāng)量測噪聲先驗(yàn)分布與真實(shí)分布不匹配時，SMC-CBMeMBer濾波算法穩(wěn)定性難以保證，由于RE-CBMeMBer濾波算法不依賴于量測噪聲的先驗(yàn)分布，因此，具有更高的穩(wěn)定性。

4 結(jié)論

本文提出了一種能在量測噪聲分布未知的情況下進(jìn)行多目標(biāo)跟蹤算法，與傳統(tǒng)的SMC-CBMeMBer濾波算法相比，該算法不依賴于量測噪聲先驗(yàn)分布，能在未知且復(fù)雜的量測噪聲分布環(huán)境下進(jìn)行多目標(biāo)跟蹤，此外該算法避免了在多維量測空間計(jì)算似然函數(shù)，與SMC-CBMeMBer算法相比，節(jié)省了近40%的時間，算法實(shí)時性得到提高。