基于非線性Wiener過(guò)程的步進(jìn)加速退化建模方法*

解 江，蔡忠義，項(xiàng)華春

（1.西京學(xué)院，西安 710123；2.空軍工程大學(xué)裝備管理與無(wú)人機(jī)工程學(xué)院，西安 710051）

0 引言

隨著科學(xué)技術(shù)的發(fā)展，高可靠長(zhǎng)壽命產(chǎn)品不斷涌現(xiàn)，使得傳統(tǒng)基于額定應(yīng)力的試驗(yàn)方式難以適用，促進(jìn)了加速退化試驗(yàn)技術(shù)的快速發(fā)展。通過(guò)獲取加速應(yīng)力下產(chǎn)品性能退化數(shù)據(jù)，外推產(chǎn)品的壽命分布函數(shù)以及相關(guān)壽命信息已經(jīng)成為當(dāng)前可靠性領(lǐng)域研究的熱點(diǎn)。

Wiener過(guò)程是一種具有平穩(wěn)、便于計(jì)算與分析特性的隨機(jī)過(guò)程模型，廣泛應(yīng)用于退化建模。當(dāng)產(chǎn)品的性能退化過(guò)程呈現(xiàn)出總體均勻變化，而個(gè)體之間的退化差異會(huì)隨時(shí)間增加而逐步增大時(shí)，都可用Wiener過(guò)程進(jìn)行退化過(guò)程建模。目前利用Wiener過(guò)程來(lái)建模加速退化數(shù)據(jù)需關(guān)注兩個(gè)方面的問(wèn)題。

1）非線性特征。由于受到噪聲、擾動(dòng)等不確定性因素的影響，產(chǎn)品在退化過(guò)程中常常呈現(xiàn)出非線性特征，一般可采用兩種方法進(jìn)行處理：一是非線性數(shù)據(jù)的線性化處理。Whitmore首先提出時(shí)間尺度模型的概念，將非線性數(shù)據(jù)轉(zhuǎn)化為線性數(shù)據(jù)［1］。王浩偉等［2］、蔡忠義等［3］采用時(shí)間尺度模型，將非線性步進(jìn)加速退化數(shù)據(jù)轉(zhuǎn)化線性退化數(shù)據(jù)。由于該方法計(jì)算過(guò)程簡(jiǎn)單，應(yīng)用也較為廣泛［4］。二是直接建立非線性Wiener退化建模，推導(dǎo)出產(chǎn)品失效的概率密度函數(shù)［5］。通過(guò)模型誤設(shè)研究［6］，表明后者的評(píng)估精度要高于前者。

2）隨機(jī)效應(yīng)。隨機(jī)效應(yīng)是指不同產(chǎn)品在退化過(guò)程中的個(gè)體差異。對(duì)于Wiener退化模型而言，一般將Wiener過(guò)程的參數(shù)看作為隨機(jī)系數(shù)，以體現(xiàn)退化過(guò)程中的隨機(jī)效應(yīng)。蔡忠義等［7］、Wang等［8］將 Wiener過(guò)程的漂移系數(shù)和擴(kuò)散系數(shù)都看作是隨機(jī)變量并假定其先驗(yàn)分布類型為正態(tài)-逆伽瑪分布，由于建模過(guò)程較為復(fù)雜，難以直接給出含有雙隨機(jī)系數(shù)的概率密度函數(shù)表達(dá)式，可能會(huì)影響預(yù)測(cè)精度。Peng等［9］、唐圣金等［10］認(rèn)為個(gè)體之間的隨機(jī)效應(yīng)主要受漂移系數(shù)的影響，僅將漂移系數(shù)看作正態(tài)型隨機(jī)變量，進(jìn)而推導(dǎo)出了產(chǎn)品失效的概率密度函數(shù)的近似表達(dá)式。

因此，本文針對(duì)非線性步進(jìn)加速退化數(shù)據(jù)，推導(dǎo)出考慮非線性和隨機(jī)效應(yīng)的產(chǎn)品失效概率密度函數(shù)，建立與產(chǎn)品退化數(shù)據(jù)特征相匹配的步進(jìn)加速退化模型，采用兩步極大似然估計(jì)法來(lái)求解模型中未知參數(shù)。

1 非線性Wiener過(guò)程

假設(shè)產(chǎn)品的關(guān)鍵性能退化參數(shù)僅有一個(gè)且退化過(guò)程X（t）可用一元非線性Wiener過(guò)程描述如下：

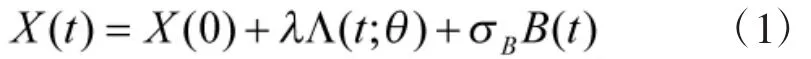
假設(shè)產(chǎn)品的失效閾值為w，則X（t）的首達(dá)時(shí)（即退化量X（t）首次達(dá)到失效閾值w的時(shí)間T）服從逆高斯分布，由此可推導(dǎo)出產(chǎn)品失效的概率密度函數(shù)表達(dá)式。

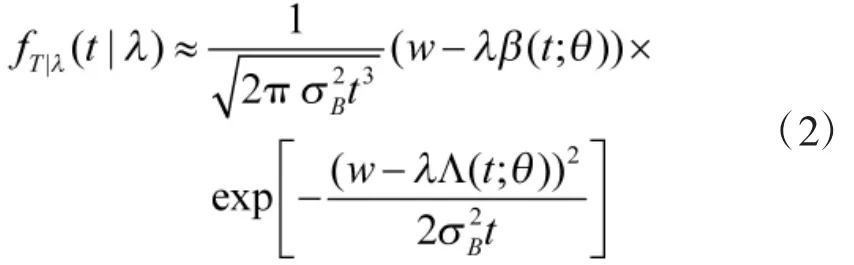
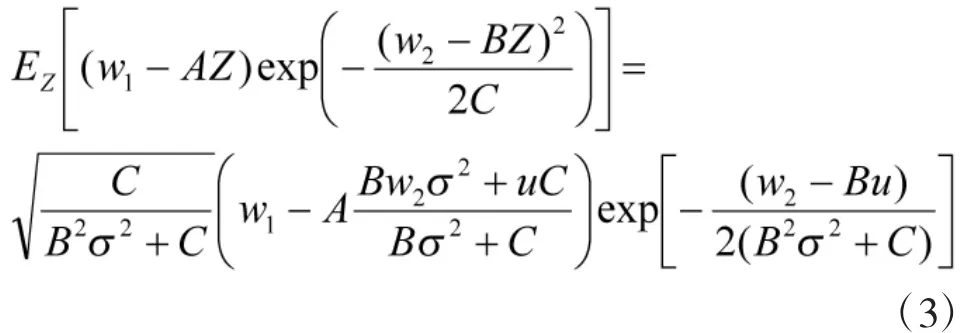
其中：

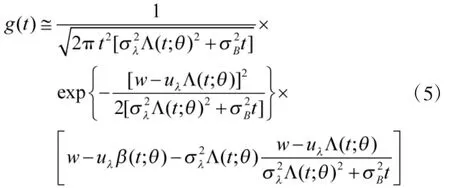
2 步進(jìn)加速退化建模

2.1 模型假設(shè)

1）選擇溫度為加速應(yīng)力、Arrhenius模型為加速模型；

2）產(chǎn)品在加速應(yīng)力下發(fā)生的退化不可逆且退化機(jī)理不變；

3）產(chǎn)品性能退化量在實(shí)際測(cè)量過(guò)程中的測(cè)量誤差暫不考慮。

2.2 步進(jìn)加速退化模型

現(xiàn)有m個(gè)產(chǎn)品在n個(gè)加速應(yīng)力下進(jìn)行步進(jìn)加速退化試驗(yàn)。試驗(yàn)應(yīng)力記為S1，S2，…，Sn。已知每個(gè)加速應(yīng)力下各測(cè)量K次產(chǎn)品的性能退化參數(shù)，得到的試驗(yàn)數(shù)據(jù)具有平衡試驗(yàn)數(shù)據(jù)結(jié)構(gòu)。將應(yīng)力Si下產(chǎn)品j第k個(gè)測(cè)量時(shí)刻記為，此時(shí)對(duì)應(yīng)的性能退化數(shù)據(jù)記為，i=1，2，…，n；j=1，2，…，m；k=1，2，…，K。步進(jìn)應(yīng)力加速退化試驗(yàn)過(guò)程見(jiàn)圖1所示。

圖1 步進(jìn)應(yīng)力加速退化過(guò)程

由圖1可知，當(dāng)前加速應(yīng)力下產(chǎn)品退化量初值是前一應(yīng)力下退化量末值，即，從而建立各加速應(yīng)力下性能退化量X（t）的關(guān)系模型如下：

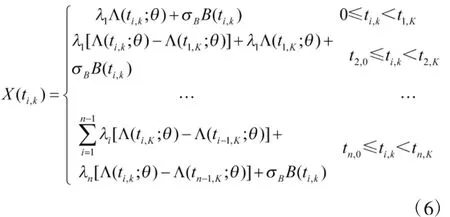
式中，X（ti，k）為應(yīng)力 Si下第 k 個(gè)次測(cè)量到的性能退化量；ti，k為對(duì)應(yīng)的測(cè)量時(shí)刻；i為應(yīng)力Si下漂移系數(shù)，為描述受試產(chǎn)品之間的隨機(jī)效應(yīng)，用正態(tài)型隨機(jī)變量表示為。

2.3 加速模型

Wiener過(guò)程中漂移系數(shù)常常被認(rèn)為是與加速應(yīng)力有關(guān)的參數(shù)，因此，可采用Arrhenius模型來(lái)描述漂移系數(shù)與溫度之間的關(guān)系模型，具體為：

3 參數(shù)估計(jì)

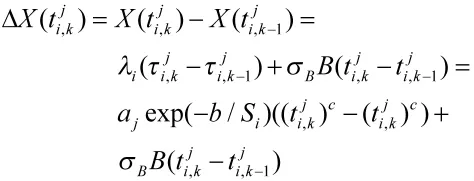
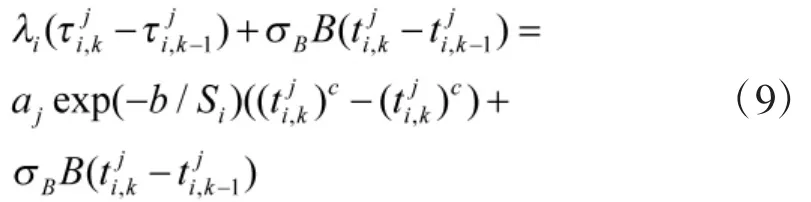
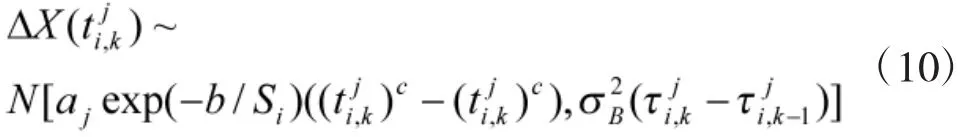
根據(jù)式（10），建立未知參數(shù)集Θ的對(duì)數(shù)似然函數(shù)為：

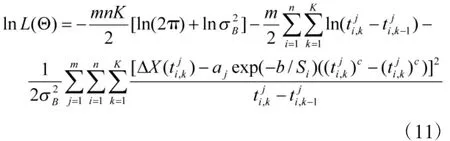
由于上式中aj相對(duì)于是隱含變量，難以直接通過(guò)傳統(tǒng)極大似然估計(jì)法求解出，但可采用兩步極大似然估計(jì)法進(jìn)行求解，即第1步，針對(duì)參數(shù)b，c的輪廓對(duì)數(shù)似然函數(shù)，求解出 b，c的估計(jì)值，進(jìn)而求解出隱含變量aj和的估計(jì)值；第2步，利用，求解出的估計(jì)值。具體求解過(guò)程如下：

首先，求解出式（11）關(guān)于 aj和的一階偏導(dǎo)數(shù)為：

然后，進(jìn)一步可求解出aj和受限于b，c的估計(jì)值為：

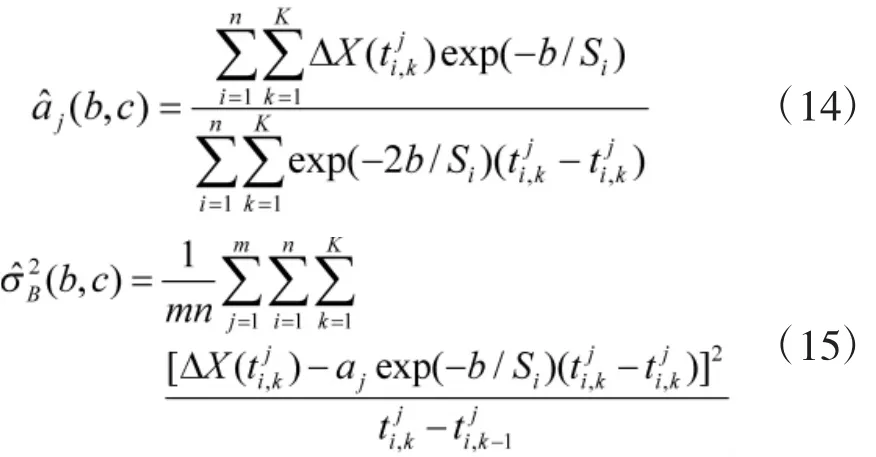
將式（14）、式（15）代入式（11），化簡(jiǎn)后即可得到參數(shù)b，c的輪廓對(duì)數(shù)似然函數(shù)為：

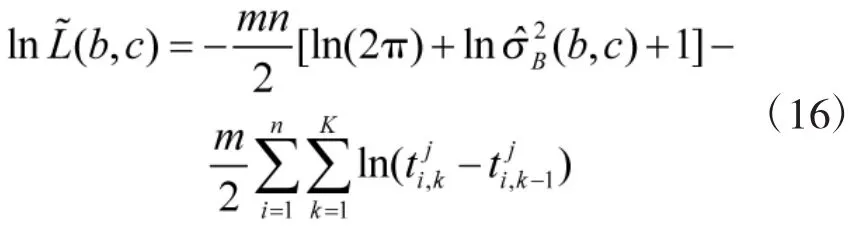
采用基于單純形法的fminsearch函數(shù)，進(jìn)行二維遍歷搜索，直到取最大值時(shí)，即可求解出b，c的估計(jì)值。將代入式（14）、式（15）即可求解出隱含變量aj和的估計(jì)值。

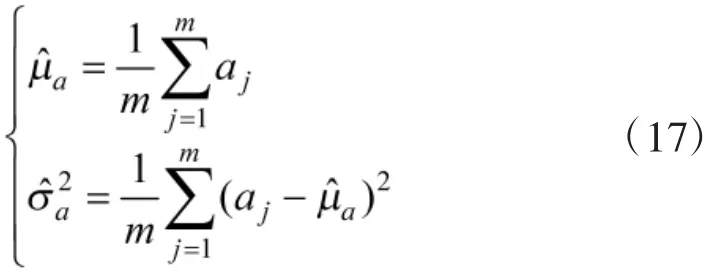
4 實(shí)例分析

已知某型激光器的關(guān)鍵性能參數(shù)是工作電流，其正常工作溫度為25℃，現(xiàn)有8個(gè)產(chǎn)品進(jìn)行步進(jìn)應(yīng)力加速退化試驗(yàn)，步進(jìn)溫度分別為35℃、55℃、75℃。每個(gè)應(yīng)力下測(cè)量5次，測(cè)量間隔為150 h。當(dāng)激光器工作電流增加量達(dá)到10 mA時(shí)，則認(rèn)定其失效。設(shè)定該激光器SSADT仿真參數(shù)的真值如表1所示，采用Monte Carlo仿真方法，得到8個(gè)樣本在SSADT中工作電流的退化數(shù)據(jù)見(jiàn)圖2。

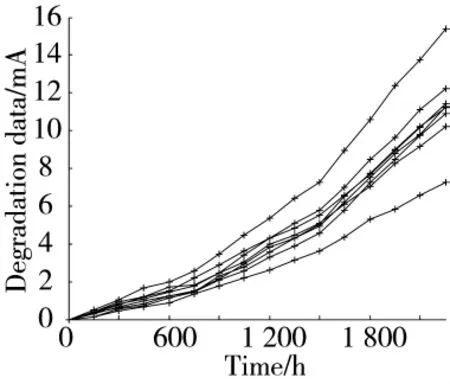
圖2 8個(gè)步進(jìn)加速退化數(shù)據(jù)樣本

為便于比較本文所提出的方法與現(xiàn)有方法之間的擬合精度和評(píng)估優(yōu)勢(shì)，將本文提出的基于非線性Wiener過(guò)程的加速退化建模方法記為M1，將文獻(xiàn)［10］提出的基于線性Wiener過(guò)程的加速退化建模方法記為M2。采用赤池信息準(zhǔn)則（AIC）和均方誤差（MSE）來(lái)判斷兩種方法模型之間的優(yōu)劣［3］。

4.1 參數(shù)估計(jì)結(jié)果

設(shè)定參數(shù)b，c的初值分別為2 600、1，采用基于單純形法的fminsearch函數(shù)進(jìn)行遍歷搜索，再將所返回的 b，c值代入式（14）、式（15）、式（17），從而求出求得。具體參數(shù)估計(jì)結(jié)果見(jiàn)表1。

4.2 方法優(yōu)劣判斷

根據(jù)AIC和MSE計(jì)算公式，計(jì)算出兩種方法之間的AIC值和MSE值見(jiàn)表2。可知，M1的AIC值和MSE值均較小，說(shuō)明M1的模型擬合精度更好。

表1 參數(shù)估計(jì)結(jié)果結(jié)果

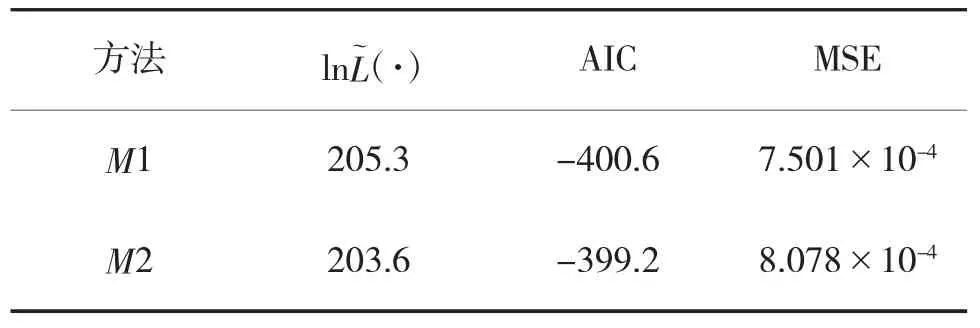
表2 兩種方法的優(yōu)劣對(duì)比

4.3 概率密度函數(shù)

將上述參數(shù)估計(jì)結(jié)果代入式（4）、式（5），可求解出激光器的概率密度函數(shù)，進(jìn)而繪制出其概率密度函數(shù)曲線見(jiàn)圖3。從概率密度曲線看，M1概率密度曲線較M2概率密度曲線更接近于真實(shí)值曲線，說(shuō)明M1的模型擬合性較好。

圖3 兩種方法的概率密度曲線

5 結(jié)論

1）本文在步進(jìn)加速退化試驗(yàn)場(chǎng)合下，提出了一種基于非線性Wiener過(guò)程的步進(jìn)加速退化建模方法，可處理非線性、隨機(jī)效應(yīng)等退化特征數(shù)據(jù)。

2）針對(duì)退化模型中多個(gè)未知參數(shù)的估計(jì)問(wèn)題，采用兩步極大似然估計(jì)法，可較好地處理參數(shù)個(gè)數(shù)多于似然方程數(shù)的場(chǎng)合，參數(shù)估計(jì)精度較高。

3）通過(guò)仿真實(shí)例分析，進(jìn)一步驗(yàn)證了本文所提出的方法比現(xiàn)有方法的擬合精度更好，從兩者的AIC值、TMSE值以及概率密度曲線也可以證實(shí)。