溫州深厚軟黏土流變模型識別及工程應用分析

劉 勇

（中鐵第四勘察設計院集團有限公司 湖北武漢 430063）

1 引言

溫州市域鐵路S1線總體為東西走向，西起沿海鐵路溫州南站南端潘橋鎮，東至靈昆半島，遠期至洞頭縣洞頭島。是構建未來溫州大都市核心區兩大中心——中心城和甌江口新城的快速聯系通道。擬建工程經過區域多屬于沖海積平原區。沖海積平原區土體厚度大，普遍發育淤泥、淤泥質黏土等特殊性軟土。這些軟黏土呈厚層狀大面積分布，層厚一般為20～60 m，具有天然含水量高、滲透系數低、排水緩慢、固結時間長、易觸變性、高壓縮性、強度低等特點，工程性質差，運營隧道會產生長期沉降和不均勻沉降問題，甚至引發安全事故。因此，溫州深厚軟土流變問題成為溫州市域鐵路運營中的關鍵問題之一［1-2］。

對于軟黏土流變特性本構模型的研究，早期主要是將固結模型與流變模型并聯或串聯后建立的組合模型為主［3-9］。后來各類新的模型不斷出現，如根據黏性土的試驗成果提出基于等效時間線的彈黏塑固結模型［10-11］及考慮排水條件的蠕變模型［12］、通過擾動狀態面模型（DSC）的多功能特征和三軸試驗成果建立的固結狀態下的土體蠕變模型［13］等等。本文對深厚軟黏土流變特性引起運營隧道長期變形規律進行分析研究，在溫州軟黏土室內流變特性試驗的基礎上，建立了軟黏土彈粘塑性本構模型研究。并將彈粘塑性本構模型應用到鐵路隧道中，重點分析了隧道運營期的流變效應。

2 考慮初始各向異性的非結構性軟黏土彈粘塑性模型

2.1 模型的建立

根據Perzyna過應力理論，將土體總的應變率分為彈性應變率和粘塑性應變率：

其中彈性應變率與時間無關，并認為是各向同性的，可以采用修正劍橋模型的方法來描述：

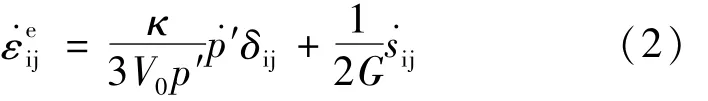
式中，κ為回彈指數；V0＝（1＋e0），為特征體積；G為剪切模量，與回彈指數κ和泊松比ν有關，G＝為平均有效應力；s˙為偏應力張ij量；δij為克羅內克符號。

根據Perzyna的過應力理論并結合流動法則粘塑性應變率可以表示為：

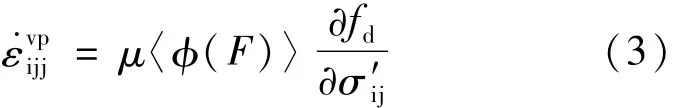
上式中μ是黏性參數；動態加載面fd被認為粘塑性勢函數（相關聯法則）；當F＞0時，［φ（F）］＝φ（F），當F≤0時，〈φ（F）〉＝0；在 Perzyna的過應力理論中φ（F）表示動態加載面與靜態屈服面之間相對距離函數，即過應力函數，反映粘塑性應變率的大小，只有當應力狀態位于靜態屈服面以外時，才會發生粘塑性流動。

當處于超固結狀態時，土體仍然會產生蠕變，說明當應力狀態位于靜態屈服面內部時依然會有粘塑性應變的產生。有必要對Perzyna的過應力理論中φ（F）進行修正。粘塑性應變率由動態加載面和參考面的相對距離函數（過應力函數φ（F））來反映，此處過應力函數φ（F）是動態加載面和參考面的相對距離的函數。不管動態加載面位于參考面的內部還是外部（對應于F≤0和F＞0），均會發生粘塑性流動，所以式（3）改寫成：

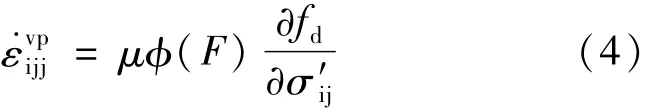
國內外對于K0固結狀態的天然軟黏土的屈服面的研究發現，由于初始各向異性導致軟黏土屈服面是一個傾斜的橢圓，但是臨界狀態線在應力空間內的斜率仍為M。本文采用Wheeler的方法對動態加載面進行研究，用如下傾斜的橢圓來反映各向異性對動態加載面和參考面的影響：

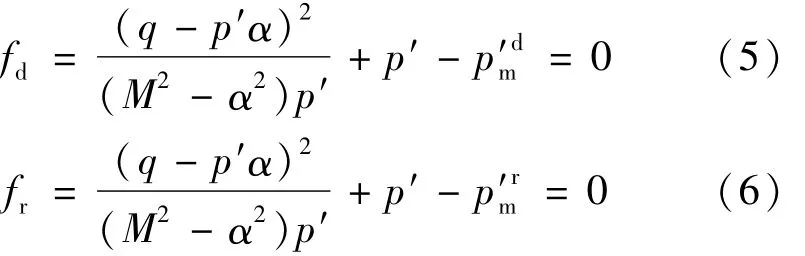
上式中α表示動態加載面和參考面的傾斜程度，是各向異性變量，表征各向異性的強弱。α0是各向異性變量的初始值，反映初始各向異性的影響。當α0＝0時，上述屈服面退化為MCC模型的屈服面。當考慮各向異性隨粘塑性應變發生演化時，α也隨之發生變化。

上式中q表示偏應力大小；p′為平均有效應力；M為臨界狀態線的斜率為動態加載面與α軸交點在p′軸上的投影，表示動態加載面的大小為參考面與α軸交點在p′軸上的投影，表示參考面的大小；與修正劍橋模型類似，參考屈服面采用體積硬化準則：

動態加載面上任意一點的法向量在p′軸和q軸的投影分別為：

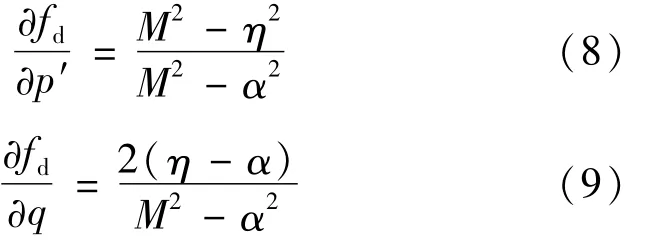
式中，η為有效應力比，η＝q／p′

根據式（4）并結合式（8）、（9）得到三軸應力條件下的粘塑性體積應變率和粘塑性偏應變率的表達式：

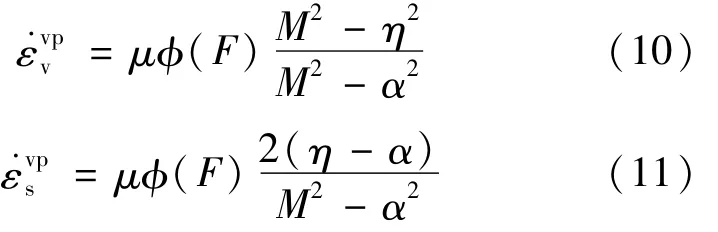
對于一維加載情況，η＝ηK0，α＝α0，則一維加載情況下的粘塑性體積應變率由式（10）得到：

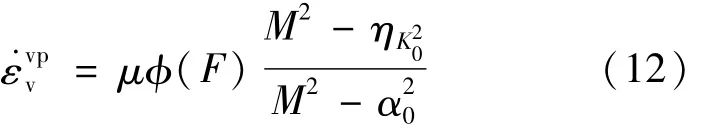
將p′換成σ′v便可得到一維情況的體積粘塑性應變率：

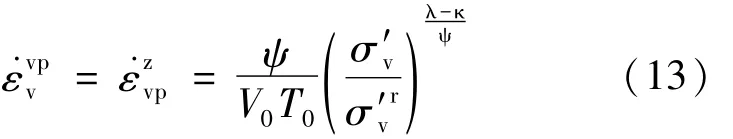
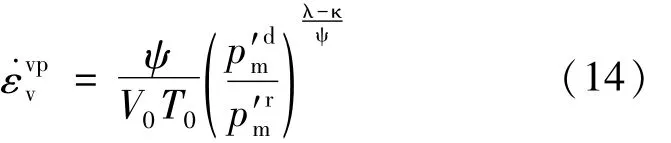
對比式（12）和式（14）可得到過應力函數的一種表達式：

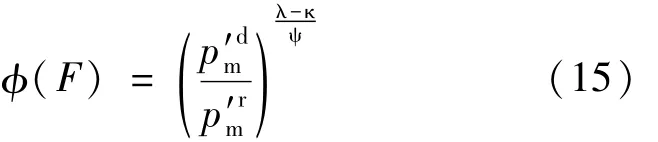
從過應力函數的表達式可以看出，任意動態加載面上過應力函數相等，與前文假設條件相符。聯立式（1）、（2）、（4）、（5）、（7）、（15）只考慮初始各向異性軟黏土三維彈粘塑性本構模型。

2.2 參數確定

從建立的理論模型可以看出，模型參數包括修正劍橋模型參數、初始各向異性參數、黏性參數。

（1）修正劍橋模型參數

修正劍橋模型參數包括回彈指數κ、壓縮指數λ、泊松比ν、初始孔隙比e0、臨界狀態應力比M、初始參考面的大小κ、λ、e0可以通過一維壓縮試驗獲得；M、ν可由三軸試驗獲得：M＝6sinφ′／（3-sinφ′）可以由一維參考前期固結應力確定如式（16）所示：

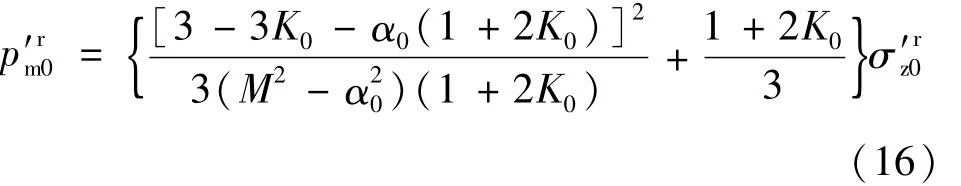
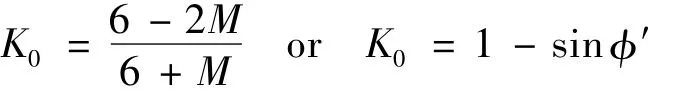
（2）初始各向異性參數

天然軟黏土K0固結引起的初始各向異性可由以下方法定量確定。在三軸應力條件下，很容易求得：

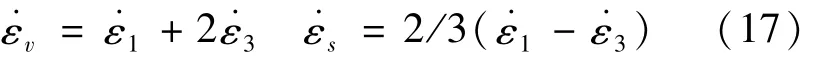
忽略彈性偏應變得到：

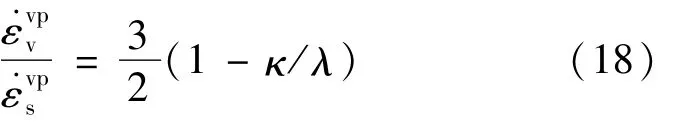
由式（10）、（11）得到：

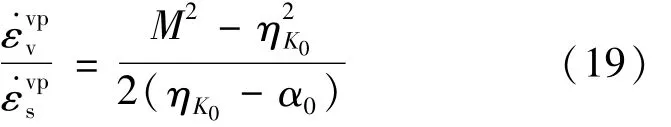
上式中 ηK0＝3（1-K0）／（1＋2K0）。聯立式（18）、（19）得到：

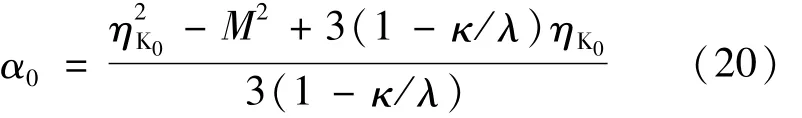
（3）黏性參數

聯立式（12）、（14）、（15）可以得到黏性參數 μ的表達式：

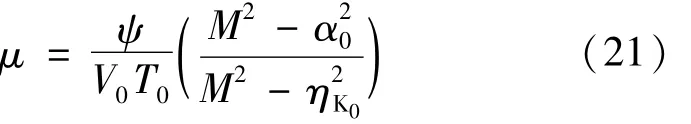
3 溫州深厚軟黏土流變試驗及模型驗證

為了驗證模型的正確性，本文通過加拿大Sackville地區黏土、溫州、日本大阪三種軟黏土進行K0固結三軸不排水剪切蠕變試驗，通過得到的試驗數據與模型進行對比對模型的適用性進行驗證。

3.1 加拿大Sackville地區黏土蠕變試驗與模型對比

選用加拿大Sackville地區黏土的K0固結三軸不排水蠕變試驗來驗證所建模型。試樣首先在圍壓為56 kPa，K0＝0.76的條件下進行偏壓固結，固結完成后進行如下試驗：

試驗1：在偏應力水平q＝35 kPa下不排水蠕變時間為8 000 min。

試驗2：q＝44.5 kPa條件下不排水蠕變時間12 000 min后，當軸向應變和超孔隙水壓基本穩定以后施加下一級荷載至q＝50 kPa，再繼續不排水蠕變12 000 min。

圖1為加拿大Sackville地區黏土在q＝35 kPa、q＝44.5 kPa、q＝50 kPa下軸向應變和超孔隙水壓隨時間發展的試驗曲線和模擬曲線的對比圖。從圖可以看出隨著偏應力水平的增大，剪應變的增長速度明顯加快。除了q＝50 kPa，模型基本上能很好地描述軸向應變和超孔壓隨時間的發展規律。當q＝50 kPa時，計算得到的軸向蠕變由初始蠕變階段進入穩定蠕變階段的時間要比試驗值小；計算軸向蠕變在試驗后期已經進入加速蠕變階段，而試驗軸向應變并未進入蠕變破壞階段，這也導致計算孔壓和試驗孔壓逐漸出現偏差，即當計算的軸向蠕變開始進入加速蠕變階段，孔壓開始下降引起的。但是總體而言，本文模型能夠很好地反映加拿大Sackville地區軟黏土的蠕變特性。

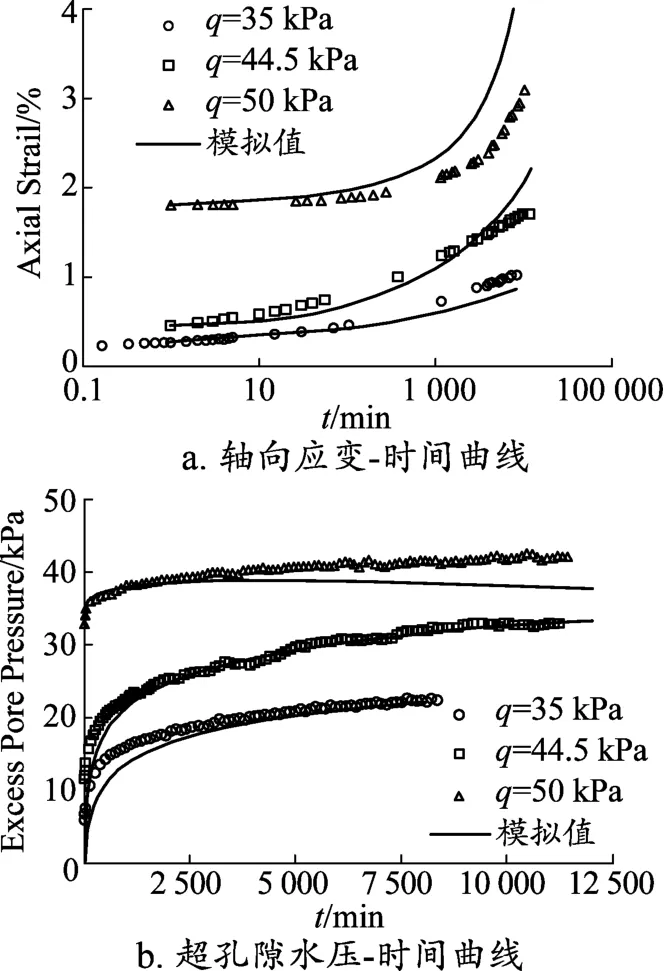
圖1 加拿大Sackville地區黏土三軸不排水蠕變的試驗曲線和模擬曲線

3.2 溫州黏土蠕變試驗與模型對比

本文對溫州10 m深的軟黏土進行了不同圍壓下的等向固結三軸不排水蠕變試驗。三軸不排水蠕變試驗采用分級加載的方式，蠕變穩定標準規定為連續1 d內軸向變形量小于0.01 mm，則進入下一級偏應力水平下的三軸蠕變試驗。現以圍壓為150 kPa的三軸不排水蠕變試驗來驗證本文模型的有效性，試驗的偏應力級別分別為q＝37.27 kPa，q＝74.54 kPa，q＝111.8 kPa，q＝149.08 kPa，q＝194.94 kPa。

圖2是計算得到的軸向應變隨時間的變化曲線和試驗曲線的對比。由圖可以看出，在所選參數條件下模型能很好地反映溫州10 m深軟黏土等向固結三軸不排水蠕變試驗不同偏應力下的軸向應變隨時間的發展規律。模型不僅能有效地預測偏應力水平較低時的初始蠕變和穩定蠕變，而且還能準確地預測偏應力水平較高時出現的加速蠕變性狀。

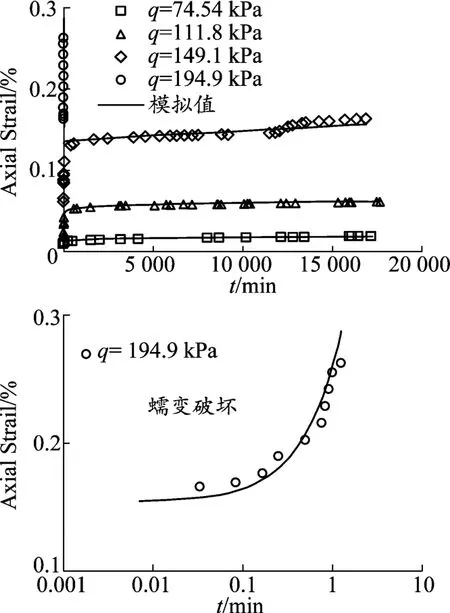
圖2 溫州10 m深軟黏土等向固結三軸不排水蠕變試驗曲線和計算曲線

3.3 日本大阪軟黏土蠕變試驗與模型對比

不排水剪切蠕變時，土體的應變和孔壓的發展與土體偏應力水平密切相關，當偏應力過大時，土體在蠕變后期的應變率不僅不減小反而會持續增大，應變加速發展，出現剪切蠕變破壞，正如溫州10 m深軟黏土在q＝194.94 kPa時出現的蠕變性狀。為了進一步驗證模型能否成功模擬軟黏土的蠕變破壞現象，針對日本大阪灣軟黏土進行三軸不排水剪切蠕變破壞試驗。圖3分別為日本大阪灣軟黏土在各種偏應力水平下不排水剪切蠕變過程中軸向應變和平均有效應力隨時間變化的試驗點與計算值比較。從圖3a可以看出，當q／p′i≥0.663后，土樣開始出現剪切蠕變破壞，軸向應變持續加速增長，而p′迅速減小至q／p′＝M為止。模型基本上能很好地描述蠕變破壞過程中的軸向蠕變應變隨時間的發展規律。從圖3b可以看出，模型對孔壓的模擬效果不如對軸向應變的模擬，這主要與模型采用的彈性應變計算式及κ取值相關。但總體而言，本文模型較好地模擬發生蠕變破壞的破壞時間及軸向應變的加速發展，說明本文考慮土體黏性的思路是正確的。

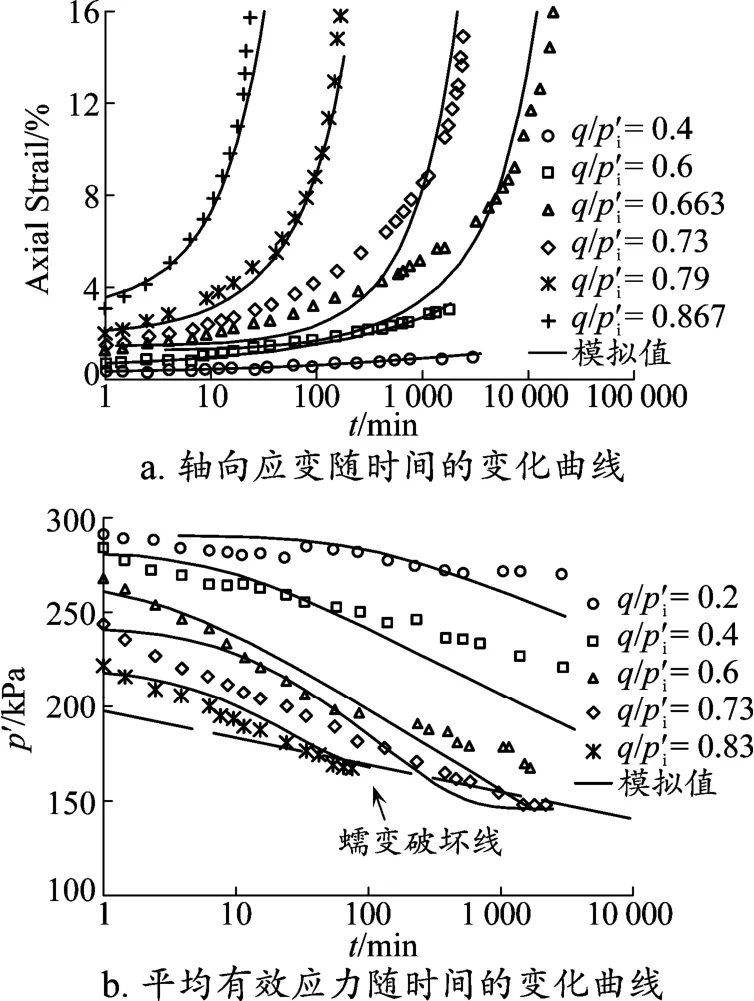
圖3 日本大阪軟黏土不排水蠕變破壞試驗曲線及模擬曲線

4 工程應用

4.1 模型參數的選用

通過試驗驗證可以發現，該模型能夠很好地模擬軟黏土的蠕變規律。本文運用本模型對溫州某區段的軟黏土隧道的蠕變規律進行數值模擬。所采用的參數如表1所示。

表1 計算參數匯總

4.2 數值模擬

ABAQUS有限元分析軟件在巖土工程計算中得到了廣泛的應用。雖然ABAQUS自帶豐富的土體本構模型，如劍橋模型、D-P模型等，但由于這些模型存在局限性，不能較全面準確地反映土體的特殊性質，如時效性、結構性、各向異性等。本文通過ABAQUS相應的用戶材料子程序，通過UMAT子程序接口引入ABAQUS軟件中，再利用ABAQUS強大的前、后處理和先進的數值模擬技術，對軟土工程的長期變形和長期穩定性進行預測和模擬研究。

對軟黏土盾構隧道長期變形的數值模擬采用二維平面應變計算模式，計算過程中采用不同的時間步和與其相應的工況來模擬隧道施工期、隧道運營期的變形發展規律。以溫州城域鐵路某盾構區間隧道為工程背景，模型的水平和豎直方向的長度均為60 m，隧道中心埋深20 m。數值計算中以隧道軸線為對稱軸，其數值模型及單元劃分如圖4所示。土體單元類型為CPE4單元，其本構模型為采用本文建立的彈粘塑性模型。隧道襯砌采用三角形單元，其本構模型為彈性模型。在計算時假設管片拼裝完成后，襯砌與土體始終保持接觸狀態且不會發生滑移，所以襯砌與土體之間的接觸面采用綁定約束。

圖4 數值模型及單元劃分

本文主要考慮地鐵運營期軟黏土流變特性對隧道長期變形的影響，因此，對隧道復雜的施工過程進行簡化處理。設置如下計算分析步：（1）設置初始地應力平衡；（2）對開挖區土體模量折減以達到應力釋放的效果；（3）將開挖區的土體單元 “移除”并同時“添加”襯砌單元；（4）設置長期流變計算，根據地鐵隧道的設計使用年限，流變計算時間為100年。由于隧道埋深較大，隧道施工引起的隧道周邊的超孔隙水壓難以消散，所以將地表作為不排水邊界近似處理。位移邊界條件為：地表不受約束、模型底面約束豎向位移、模型側邊豎向位移自由、約束橫向位移。

4.3 結果分析

圖5是地表沉降的分布規律，由圖可以看出，由于軟黏土存在很顯著的流變特性，因此隧道施工引起的沉降槽會隨時間逐漸發展，沉降槽隨時間有整體下降的趨勢，地表沉降也隨時間逐漸增大。施工完成后100 d的隧道正上方地表沉降為42.48 mm，和施工完成時相比幾乎沒有變化。施工完成后1 000 d時隧道正上方地表沉降為44.56 mm，相對于施工期沉降增加了5.5%。施工完成10 000 d后的地表沉降最大值為54.93 mm，比施工期沉降增加了30%。隧道建成100年時隧道正上方地表沉降為74.67 mm，比施工期沉降增加了32.4 mm，增加了近76.7%。通過以上分析可知，軟黏土流變特性引起的地鐵隧道的長期沉降是很顯著的。這對地鐵的長期運營安全是一個極大的挑戰，因此對隧道長期變形機理和控制措施的研究具有重要的工程意義。

圖5 地表沉降時空分布規律

圖6是距隧道軸線10 m處豎直測線L的水平位移隨時間的變化規律。隧道盾構施工引起的豎直測線L頂點處的水平位移為26.1 mm，隨著深度的增加，測線L上的水平位移逐漸減小，并在隧道起拱線處達到最小值；起拱線以下的水平位移隨深度先增大后逐漸不變，測線L的水平位移分布規律與襯砌橢圓化變形有一定的關系，襯砌拱頂向隧道中心移動，襯砌起拱線處同時遠離隧道中心擠壓土體，導致了測線L起拱線處的水平位移最小。另外由圖可以看出，相對于地表沉降，軟黏土流變對地層水平位移的影響較小，隧道建成100年后隧道起拱線處的水平位移只增加了1.6 mm。

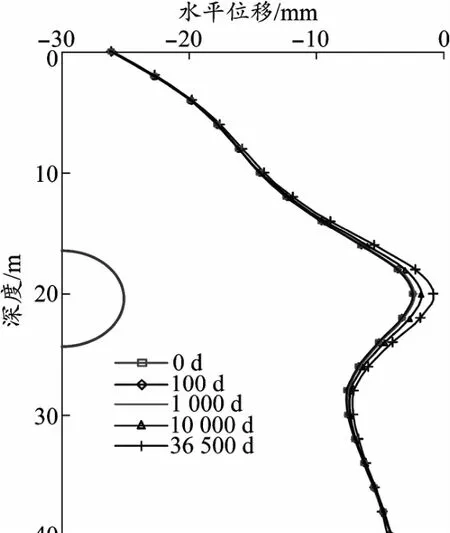
圖6 測線L的水平位移隨時間的變化規律

5 結論

（1）本文在理論推導的基礎上建立了溫州深厚軟黏土彈粘塑性本構模型，并通過加拿大Sackville地區軟黏土，溫州軟黏土和大阪軟黏土的流變試驗，驗證了模型的可靠性。結論表明，該模型可以較好地模擬隧道運營期的流變效應。

（2）以ABAQUS為平臺，建立深厚軟黏土盾構隧道的有限元計算模型，對深厚軟黏土盾構隧道的長期變形進行數值模擬研究，探討了軟黏土流變性對深厚軟黏土盾構隧道長期變形的影響規律。本研究可以為深厚軟黏土盾構隧道的設計、施工、監測、運營提供一定的理論依據。