面向時間協同的多無人機隊形變換最優效率模型

顧偉，湯俊，白亮，老松楊

國防科技大學 系統工程學院，長沙 410073

在戰場使用中，無人機通常需要根據任務要求集結成具有一定形狀的編隊；在執行任務期間則要保持一定的編隊形狀，從而提高任務完成能力；而當戰場環境發生變化時，無人機編隊則必須進行編隊重構，才能保證編隊的生存能力。無人機編隊是由具有自主控制能力的多架無人機按照指定的隊形位置排列形成的一個較大規模的無人機集群。在一定的控制器作用下，不僅能使編隊中所有的無人機在飛行過程中保持隊形的穩定，協同完成各項任務，而且可以進行隊形的實時調整［1－2］。

相對于單無人機，多無人機構成的編隊具有更大的優勢［3］。在目標偵查時，由多架無人機同時從多個角度進行探測可以獲取目標的多維立體信息［4］；在戰場打擊中，多架無人機協同配合進行飽和式的全方位打擊，可以有效增強殺傷能力，進一步提高目標毀傷概率［5］；另外，通過合理的隊形編排，可以使編隊中的無人機更好利用其他成員產生的上升氣流，提高氣動效率、減小能源消耗，進而增強無人機編隊的續航能力［6］。

對于無人機編隊隊形變換的航跡規劃，許多研究人員把無人機的隊形變換過程抽象成一個最優化問題，優化目標是整個過程的持續時間和能源消耗函數，需要考慮的約束條件包括無人機自身的性能約束以及無人機與其他成員之間的碰撞約束［7］。華思亮等［8］通過分析無人機編隊隊形變換任務的耦合特性、碰撞避免以及編隊拓撲動態變化等問題，提出了編隊隊形變換問題的數學模型，并利用模型預測控制算法進行求解。熊偉等［9］利用控制作用參數化以及時間離散化，將無人機編隊隊形變換的時間最優問題轉化為一種帶自由末端狀態約束的離散型優化問題，并采用改進的遺傳算法進行解算，取得了較好性能。王祝等［10］利用離散化和凸近似方法將無人機航跡規劃問題轉化為凸優化問題，并基于罰函數序列凸規劃進行求解。Ajorlou等［11－12］建立了基于人工勢場的編隊控制系統。

另外還有概率法、圖論法、各類智能優化法等等，但是以上這些航跡規劃方法大部分都是給定隊形變換的起點和終點，通過賦予一定的任務要求或者在起點和終點間設置障礙，然后求解一條從起點到終點的最優路徑。但是實際中有些情況僅需要多架無人機集合成某一隊形待命，這時候隊形變換的終點位置是未知的。顯然，選擇不同的終點位置，其隊形變換的效率是不同的。另外，多無人機路徑規劃效率的評價標準比較復雜，單無人機路徑規劃可以將路徑最短、安全無碰撞作為最優標準，但是對于多無人機而言，縮小某一單架無人機的路徑長度必然會增加剩余無人機的飛行路徑，在增加時間協同要求后，即要求同時到達后，其情況更為復雜。總體而言，在無人機編隊的研究中，尋找連接確定起點和終點的最佳路線的方法很多，通過效率衡量方式，求解隊形變換空間最優位置的方法相對較少。

本文將隊形變換能源消耗與隊形變換完成時間確定為效率衡量指標，提出無人機隊形變換的最優效率模型。根據無人機編隊在實際情況中可能遇到的幾種具體的隊形變換問題，基于編隊集結、編隊保持和編隊重構等不同特點，給出了這些具體隊形變換下的最優效率計算公式，從而獲得隊形變換的最優空間位置，最后進行了仿真實驗驗證。

1 隊形變換問題描述

無人機的隊形變換問題［13］主要是指一定數量的無人機根據變換要求移動位置，形成新的隊形形狀。如圖1所示，無人機由矩形編隊A1～A6變換到目標三角編隊B1～B6。影響隊形變換效率的因素包括兩個：一個是隊形變換的最終目標位置，另一個是變換時選擇的路線。在目標位置確定時，選擇不同的路線，其消耗是不同的。同樣，當固定飛行方式時，如都為勻速直線運動，選擇不同的目標終點，隊形變換的效率也是不同的。因此選擇合適的目標位置和變換路徑對于快速、高效完成整個隊形變換有著重要意義。本文主要是固定飛行方式，利用效率衡量指標，求取隊形變換的最佳目標位置。隊形變換中的最優效率包括能源消耗最小以及完成時間最短。

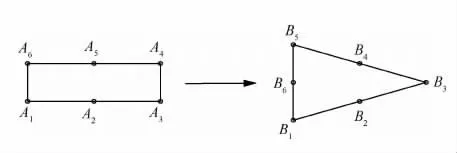
圖1 隊形變換Fig.1 Formation transformation

記編隊中的各無人機為 UAVi（i＝1，2，…，n），n為編隊中無人機的數量，UAVi在隊形變換前的位置為Ai，變換后的位置為Bi（Ai，Bi∈R3）。無人機UAVi從Ai移動到Bi走過的路程為si，所產生的能源消耗為wi，花費的時間為ti。則無人機編隊在隊形變換中的總能耗為

1.1 最小能耗變換

為了簡化研究問題，假設所有無人機均進行勻速運動，不考慮轉彎能耗以及外界環境的影響。顯然，在無障礙環境中，只要目標隊形的位置確定，無人機采取勻速直線運動，在無碰撞的情況下，一定是能耗最小、時間最短。如果是帶始末狀態約束的固定翼無人機，也存在唯一的Dubins最短航跡。當給定起點和目標點間的航跡能唯一確定時，最優效率模型的關鍵就是要在目標集結區域中尋找相應的能耗最小和時間最短的目標編隊位置。

對于UAVi，由于存在時間協同約束，各無人機必須以相同的時間t到達指定位置，所以速度與路程呈正比，即

忽略空氣密度、迎風面積等不同造成的影響，UAVi所受阻力fi與速度的平方呈正比：

式中：k為常系數。

忽略熱效應等其他影響，為了克服空氣阻力所產生的能耗為

由式（1）、式（3）～式（5），最小能耗模型可描述為

式中：c＝k／t2，當t一定時，c為常數。

1.2 最短時間變換

最優效率的另一種評價標準是完成變換所需的時間最短。首先假設各無人機以相同的最大飛行速度vmax勻速運動，則時間ti與路程si呈正比：

再以T＝maxi∈｛1，2，…，n｝ti作為總的協同時間，令無人機UAVi以vi＝si／T的實際速度勻速運動。

由式（2）和式（7），最短時間模型可描述為

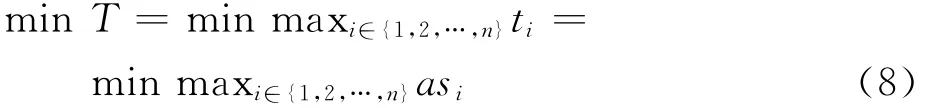
式中：a＝1／vmax為常數。

1.3 能耗-時間綜合變換

由式（6）和式（8）可以知道最小能耗與最短時間并不是一個正相關的關系，在追求最小能耗時得付出時間代價，同樣在追求最短時間時也要付出更多的能耗代價。在實際情況中往往都是要求在規定時間內完成固定形狀的編隊集結。這就是一種典型的能耗-時間綜合變換。

2 實際變換問題求解

2.1 隊形描述

在實際中，無人機編隊以平面隊形居多，因此在這里主要求解無人機的平面隊形變換問題。另外化為平面隊形后，在以后出現可能的碰撞情況時，可以實行變高避撞。在平面隊形研究中，三維空間位置變量Ai和Bi可簡化為二維平面坐標，記 Ai＝ （xi，yi），Bi＝ （xi′，yi′）。對 平 面 隊 形｛Bi，i＝1，2，…，n｝進行如下變換描述：

1）尋找隊形虛擬編隊中心

2）計算Bi和Bmiddle之間的距離

經過變換后，無人機UAVi的位置可由Bmiddle、di和θi唯一確定：

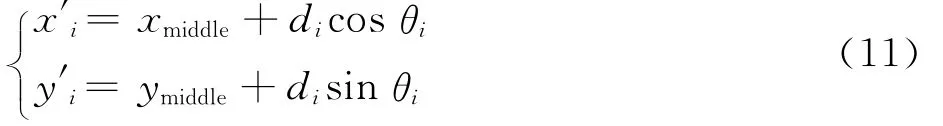
利用虛擬編隊中心法對隊形進行變換描述，可以有效減小問題規模，而且隨著無人機數量的增加，其效果越明顯。

2.2 編隊集結

編隊集結中的隊形變換主要是指一定數量的無人機按照要求形成固定隊形。在固定隊形中，di為已知量。根據不同的要求，θi可能為已知量，也可能是未知變量。例如：如果要求無人機按方向正北的三角攻擊隊形集結，θi就是已知量；如果只要求呈三角隊形，那么θi就是變量。

假設各無人機均沿直線進行勻速運動，即

2.2.1 θi已知

為了便于求解，進行一些等價變換，最小能耗模型為

模型中只有xmiddle和ymiddle兩個未知變量，利用最小二乘法求偏微分即可求解此類min問題。最短時間模型的具體計算模型為

對于這類min-max問題不能直接求解，利用文獻［14］的方法將問題轉化為帶權值的min問題，即引入權值ωi，式（14）可轉化為

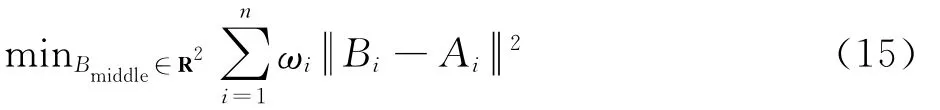
利用Lawson算法［15］進行權值迭代計算：

2）迭代ωi，ωm＋1i＝ωmiBi－Aipm，其中

3）判斷ωi值，迭代終止條件為ωm＋1i＜ε，ε為既定的極小常數，其取值視對算法的精度及對實時性能要求而定。

計算出最小能耗變換位置和最短時間變換位置后，通過加權就可以進行能耗-時間綜合變換。記最小能耗和最短時間目標隊形的虛擬編隊中心分別為

記最小能耗變換所用總時間為t1，最短時間變換所用時間為t2，t為實際的變換時間（t≥t2），則能耗-時間綜合變換目標編隊中心位置為

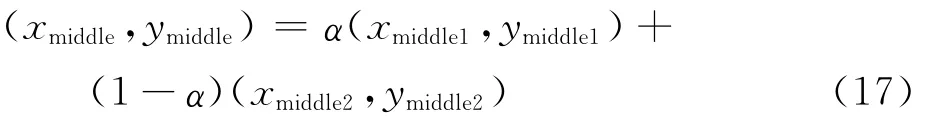
式中：t＝f（α），α∈［0，1］，且f（0）＝t2，f（1）＝t1。

2.2.2 θi未知

引入變量θ，令θi＝θ＋Δθi。其中Δθi為基準坐標下無人機UAVi與隊形中心Bmiddle的夾角，只要隊形形狀固定，Δθi為定值。θ為隊形繞中心點的旋轉角度，是一個變量。將θi＝θ＋Δθi代入式（13）得θi未知時的最小能耗模型為

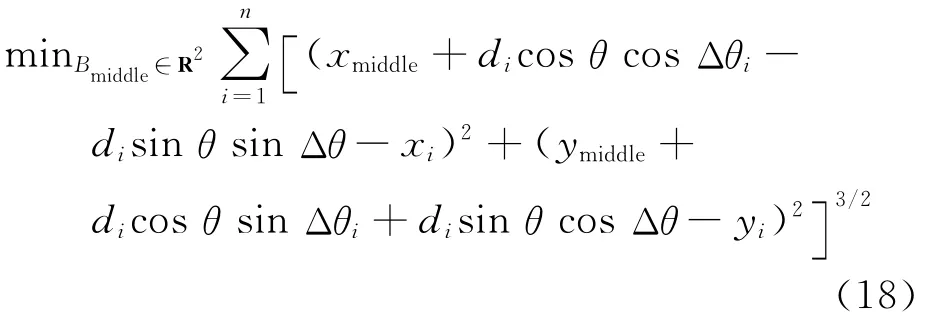
利用最小二乘法求偏微分可對式（18）進行求解。將θi＝θ＋Δθi代入式（14）得θi未知時的最短時間模型為

式（19）求解過程同2.2.1節，轉化為 min問題后利用Lawson算法進行權值迭代計算。

當θi未知時，最小能耗目標編隊位置可表示為 （xmiddle1，ymiddle1，θ1），最短時間目標編隊位置可表示為 （xmiddle2，ymiddle2，θ2），則能耗－時間綜合變換的目標編隊位置為

2.3 編隊保持

無人機編隊在飛行過程中和執行任務期間通常需要維持一定的隊形，通過平移和旋轉可以使隊形保持剛性。平移時，每架無人機的移動速度和移動距離均相等，即能耗和時間均相等；旋轉時，選擇不同的繞轉點，每架無人機的移動速度和移動距離都是不同的，選擇不同的繞轉點，能耗和時間也會有所差別。因此選擇合適的繞轉點對于快速、高效地實現隊形剛性旋轉有著重要意義。

設Bq＝（xq，yq）為繞轉點，θ為旋轉角度，則無人機UAVi移動的路程為

當指定旋轉角度θ時，最小能耗模型為

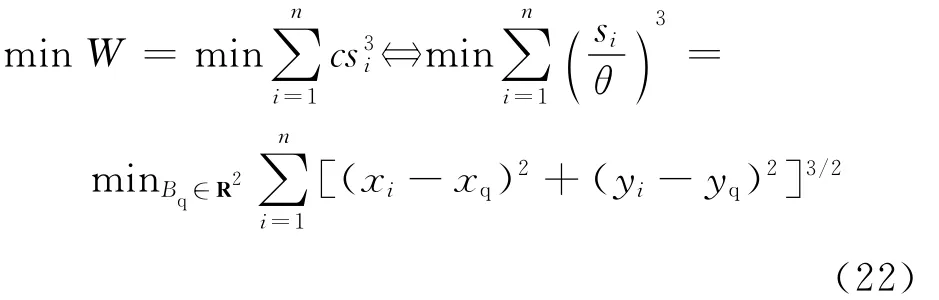
指定旋轉角度θ時，最短時間模型為

求解方法同2.2.1節。能耗-時間綜合旋轉的目標繞轉點可表示為

式中：（x1q，y1q）為最小能耗繞轉點；（x2q，y2q）為最短時間繞轉點。

2.4 編隊重構

無人機編隊在一些未知環境中飛行，威脅和障礙的出現在時間上和空間上都是隨機的；無人機編隊在執行任務時可能經受意外事故或者人為攻擊而受損。當發生這類情況時就需要進行編隊重構，進而保證無人機編隊的生存能力和任務完成能力。編隊重構［16－20］是指無人機編隊在行進過程中遇到突發情況，需要重新組織隊形。相對于編隊集結，編隊重構有更多的約束條件。例如當出現成員退出時，就要重新設計合理隊形；當遇到障礙物時，不僅需要設計合理隊形，而且還要合理設置隊形所處位置，從而使每一架無人機都能安全通過障礙物。隊形中的變量包括Bmiddle＝（xmiddle，ymiddle）、di以及夾角θi，具體增加的約束方程需要根據實際情況而定。

以6架無人機變換隊形從兩障礙物之間通過為例，如圖2所示。

利用運動分解可以將無人機的重構問題分解為集結和通過兩個部分。首先根據障礙物情況為無人機設計合適的通過形狀 （di，θi）（i＝1，2，…，6）。然后基于2.2節中的最小能耗和最短時間模型進行集結。編隊重構問題中，無人機集結之后還有后續行為，因此對于無人機的方向協同有著更高的要求，所以這里采用Dubins航跡。

已知無人機i的初始位置為Ai＝ （xi，yi），初始航向為βi，集結目標位置為Bi＝ （xmiddle＋dicosθi，ymiddle＋disinθi），航向為β′i，其中只有（xmiddle，ymiddle）是未知量。對于確定的帶航向的兩點 （Ai，βi）和（Bi，β′i），如果無人機的最小轉彎半徑固定，則存在唯一的Dubins曲線，記其長度為Di。最小能耗和最短時間模型分別為

圖2 編隊重構Fig.2 Formation reconfiguration

由于Dubins曲線沒有顯性表達式，無法利用最小二乘進行求解，因此采用遍歷搜索。遍歷全局空間的計算量較大，但是通過設置合理的限制條件可以縮小解的搜索空間，從而減小計算量。如為了保證最大安全性，可以限制無人機編隊從障礙物正中間通過，從而（xmiddle，ymiddle）的搜索空間為兩障礙物連線的中垂線。最后再加上向障礙物移動的運動分量，就可以實現安全通過障礙物。

3 實驗驗證

3.1 編隊集結

本模型是在已知所有無人機位置以及周圍環境條件下的規劃方法。首先初始化6架無人機為隨機形狀，然后根據指令要求形成邊長為200的正六邊形編隊。圖3描述了目標正六邊形上下邊平行于x軸時的最小能耗與最短時間變換時目標隊形的位置情況，即θi為常數時的隊形變換目標位置。圖4描述了目標隊形為平面任意正六邊形時的最小能耗與最短時間變換時目標隊形的位置情況，即θi為變量時的隊形變換目標位置。在利用模型計算出各無人機的目標位置后，無人機以勻速直線運動前往目標點。

表1列出了圖3中6架無人機實行θi為常數時的隊形變換前各無人機的位置以及最小能耗變換和最短時間變換后的坐標位置。

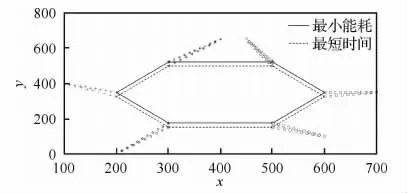
圖3 θi為常數時的變換Fig.3 Transformation with constantθi

圖4 θi為變量時的變換Fig.4 Transformation with variableθi

表2列出了圖4中6架無人機實行θi為變量時的隊形變換前各無人機的位置以及最小能耗變換和最短時間變換后的坐標位置。

表3的最優效率結果符合最優化目標，且θi為變量時，由于少了θi的約束，其最優效率（包括能耗以及時間）結果要優于θi為常數時。

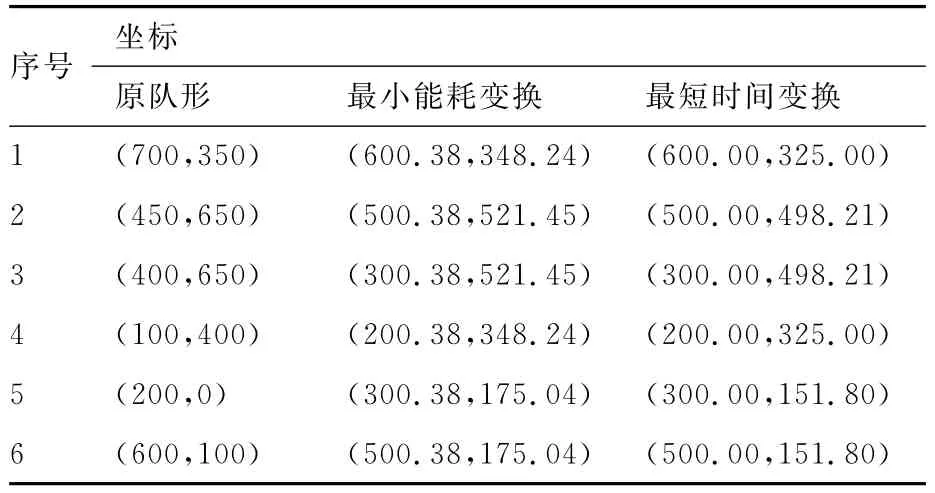
表1 固定θi變換時各無人機的坐標Table 1 Coordinates of each Unmanned Aerial Vehicle（UAV）when transforming with fixedθi

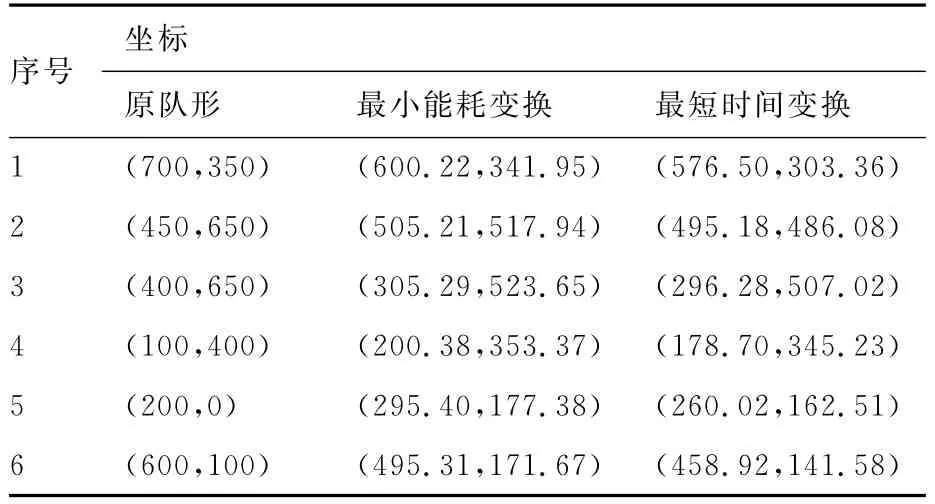
表2 不定θi變換時各無人機的坐標Table 2 Coordinates of each UAV when transforming with variableθi

表3 編隊集結各無人機移動的距離Table 3 Distance passed in UAV’s aggregation

3.2 編隊保持

為了便于觀察，首先設計一個具有明確隊形方向的編隊隊形，然后進行順時針旋轉θi＝π／2。變換結果如圖5所示。

圖5 固定隊形旋轉Fig.5 Rotation with fixed formation

從表4可以得到無人機編隊剛性順時針旋轉90°的最小能耗為19 362 456θ3c，最短時間為180.28θa。

表4 剛性旋轉各無人機的繞轉點和移動距離（θi＝π／2）Table 4 Rotation center and distance passed in UAV’s rotation（θi＝π／2）

3.3 編隊重構

隨機隊形的無人機編隊在行進過程中突遇兩個障礙物，需要縮小隊形從兩個障礙物之間通過。首先需要設計一個較窄隊形，以便于所有無人機均能順利通過障礙物，其次為了保證最大安全性，需要將無人機編隊的中心設置在兩個障礙物的中垂線上，最后讓無人機編隊沿著中垂線通過障礙物。已知障礙物1設置于（800，500），障礙物2設置于（700，673.2）。

首先計算障礙物的中垂線以及障礙物之間的距離以便于設計合理目標隊形。表5給出了一種可行的隊形設計。

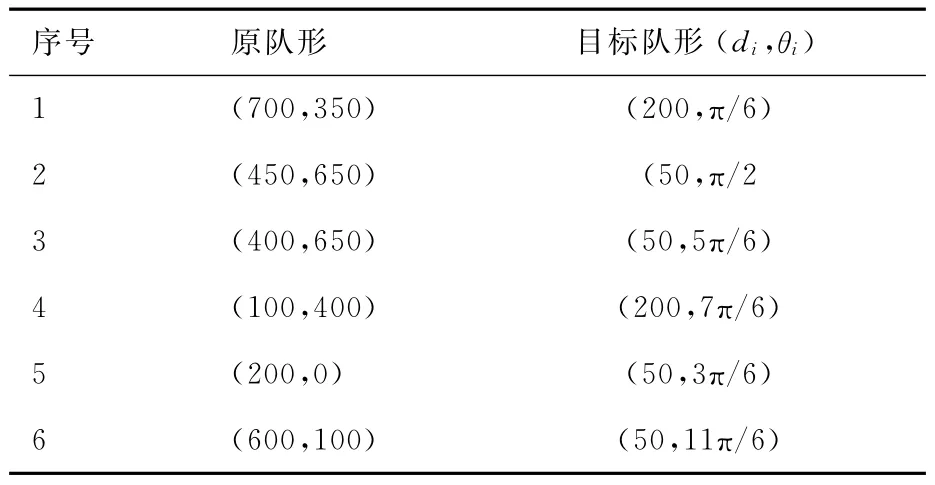
表5 無人機偏隊的目標隊形Table 5 UAV formation’s target formation

圖6為無人機編隊重構隊形從障礙物中間通過示意圖。將無人機UAVi的速度分解為vi＝，其中為原隊形向目標隊形進行集結的速度，為無人機編隊向目標方向前進的速度。合理設置速度分量的大小可以實現安全高效通過障礙物。當無人機編隊距離障礙物過近時，可以增大，減小，甚至可以將置為0以先實現原地隊形變換；當無人機編隊距離障礙物較遠時，只要滿足在到達障礙物前形成目標隊形，可以適當減小以節約能源，增大以減小編隊到達目標點的時間。

圖6 無人機編隊重構隊形從障礙物中間通過Fig.6 Going through obstacles by formation reconfiguration

3.4 避撞策略

無人機均進行勻速直線運動可能會發生碰撞情況。如圖7所示，6架不同起點的無人機對一靜止目標進行快速包圍，是一種典型的θi未知時的最短時間集結問題。

圖7 靜止目標包圍Fig.7 Surrounding stationary target

為了防止編隊成員之間發生碰撞，實行變高避撞。雖然不一定是最優，但是改變飛行高度可以有效解決碰撞沖突，另外無人機執行任務時一般飛行距離較遠，在遠距離情況下，實行變高飛行的路程代價相對較小。具體流程如下：

1）在軌跡圖上尋找距離較近的點組。

2）計算各無人機到達該點組時的時間，如果時間差小于安全時間，則標記為沖突點。其中，安全時間等于無人機間的最小安全距離除以經過該沖突點組所有無人機的最小速度。

3）計算發生沖突時，各無人機離各自終點的距離，距離越大的優先級越高。

4）優先級低的無人機將會發生沖突的軌跡點上移。

4 結 論

1）本模型的最優效率指標是利用路程推導的，具有一般性，可適用于多類無人機。

2）將編隊保持視為編隊整體的平移和旋轉，因此僅適用于松散的無人機編隊，緊密無人機編隊和有轉彎半徑的固定翼無人機無法繞內點進行旋轉。

3）無人機編隊要保持一定隊形，各無人機的速度和航向都必須要保持一致，本文沒有考慮各無人機時間協同到達目標點后的速度協同問題，將在下一步研究中進行考慮。

由于無人機防撞是一個非常復雜的問題，本文只簡單考慮了軌跡規劃時的編隊成員之間的避撞。