基于改進多目標布谷鳥搜索算法的翼型氣動優化設計

張鑫帥，劉俊＊，羅世彬

中南大學 航空航天學院，長沙 410083

在飛行器設計領域中，增升減阻是大型飛機氣動設計的核心問題［1］，以前氣動外形的選型是依據設計者憑經驗進行試湊，然后在風洞中進行試驗，看是否滿足氣動要求。這樣設計很難使性能達到整體最優，不僅設計周期很長，而且耗費了大量的人力和物力。隨著計算機技術的發展，應用CFD技術和優化算法相結合來進行氣動外形優化設計成為飛行器設計的主要手段之一［2］。氣動函數一般表現為多峰值函數，基于梯度的優化方法容易陷入到局部最優，而無梯度的元啟發式智能優化算法強大的全局尋優能力對于解決氣動優化問題非常有利。現代大型民用飛機設計中，人們對飛機的性能提出了更苛刻的要求，精細化和多目標綜合設計成了大型民用飛機設計的最明顯特征［3］，在飛機的優化設計中有了更復雜的目標函數和約束條件。這時，需要發展高效的元啟發式智能優化算法來解決這種復雜的優化問題。目前較為流行的元啟發式智能優化算法有模擬退火算法［4］、粒子群優化（PSO）算法［5］、蟻群算 法［6］以及遺傳算法（GA）［7］等，其中一些算法已經在氣動優化設計中被廣泛使用。

布谷鳥搜索（CS）算法是一種新型的受自然現象啟發的元啟發式優化算法。它是由Yang和Deb于2010年提出［8］，基于布谷鳥繁殖行為啟發而來。該算法引入Levy飛行機制而不是使用簡單的隨機游走策略來使得其具有更有效的全局搜索能力，它相較于遺傳算法擁有更少的代碼和更簡單的參數設置，相較于粒子群優化算法具有更好的全局收斂能力［8］。目前，CS算法在很多領域中都有廣泛的應用［9］，文獻［10］使用CS算法在神經網絡中尋找最優參數，得到了更加精準的預測模型。文獻［11］將CS算法應用于人臉識別中，相較于蟻群算法和粒子群優化算法具有更好的效果，文獻［12］應用CS算法求解整數規劃問題，結果顯示其相較于粒子群優化算法擁有更好的性能。

鑒于單目標CS算法的優秀性能，Yang和Deb［13］發展了一種直接求解Pareto最優解集的多目標智能優化算法——多目標布谷鳥搜索（MOCS）算法。目前，該算法仍處于驗證階段，較少用于工程優化設計特別是氣動優化設計中。

本文針對原始MOCS算法的不足，分別從收斂速度、收斂精度、解的均勻性3個方面對MOCS算法進行改進。通過引入非支配排序和擁擠距離來改進解的適應度評估；通過改進隨機游走策略來提高算法的局部搜索能力；通過引入改進的自適應丟棄頻率策略來提高算法的收斂速度；通過引入檔案管理機制，來提高Pareto解集分布的均勻性。隨后，將改進的多目標布谷鳥搜索（IMOCS）算法應用于翼型的Pareto多目標氣動優化設計中，得到了一系列Pareto最優解集，其中幾個解的氣動性能比基準翼型性能大幅提升。

1 多目標布谷鳥搜索算法

布谷鳥搜索算法是通過對自然界中布谷鳥繁殖行為的仿真模擬發展而來的一種新的元啟發式智能優化算法。文獻［8］中利用標準測試函數算例將CS與PSO和GA算法進行比較，CS算法相較于其他兩種算法大幅度降低了迭代次數，并提高了找到全局最優解的成功率，尤其是對于不確定性的隨機測試函數，CS算法的表現更好。自從CS算法提出之后，它憑借其優秀的搜索能力解決了很多工程優化問題從而吸引了許多研究人員的注意。Yang和Deb提出的多目標布谷鳥搜索算法［13］驗證了布谷鳥搜索算法解決多目標優化問題的可行性，從而，布谷鳥搜索算法開始應用于多目標優化領域。

為了更加簡單地實現MOCS算法，對于有k個不同目標的優化問題，引入3條理想化的規則［14］。

1）每一只布谷鳥同時產k枚鳥蛋，并將這k枚鳥蛋隨機地放置在一個鳥巢中。第k枚鳥蛋就表示著一組解的第k個目標。

2）每一代中高質量的鳥蛋所在的鳥巢是最好的鳥巢，它將在下一代中繼續繁殖。

3）每個鳥巢以Pa的概率被丟棄，這時會根據與宿主鳥蛋的相似性和相異性而搭建一個有k個鳥蛋的新鳥巢。

對3個規則進行數學分析，第1條規則其實是一個隨機選取的過程，新解通過Levy飛行進行隨機生成。同時，在這組解中進行隨機排列是交叉的過程。算法運行過程中，每一個鳥巢都以這種方式生成。第2條規則是精英保留策略，將適應度高的解一直保留到下一次迭代，這樣可以使得算法收斂到想要的結果。第3條規則認為是變異的過程，使得較差的解根據跟其他解的相似度按一定概率丟棄生成新解，這表明變異過程是一個矢量運算，它通過Levy飛行和兩組解之間的差得到。根據上面3條理想化的規則，可得到MOCS算法的實現流程，如圖1所示，其偽代碼見 Algorithm 1［13］。

通過Levy飛行生成t＋1代新解：

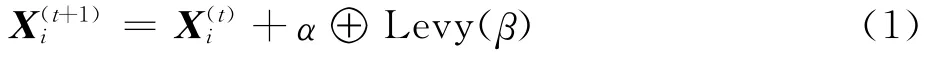
式中：符號表示矩陣的每個元素對應相乘；α的大小和問題的搜索域相關，當α較大時，算法的游走步長相對來說會變大，這樣可以更有效地去探索大尺度搜索域。通常α取為α＝o（1）。為了使算法有更快的收斂能力，可以引入不同解之間的差來使算法具有一定的變步長能力，這時α可表示為

式中：α0為一個常數。這樣可以使得相似的鳥蛋具有較低被發現的可能性。

Levy飛行機制提供了一個步長服從Levy分布的隨機游走：

Yang和Deb提出了一個簡單的模型用來實現Levy飛行［13］，這個模型可以描述為

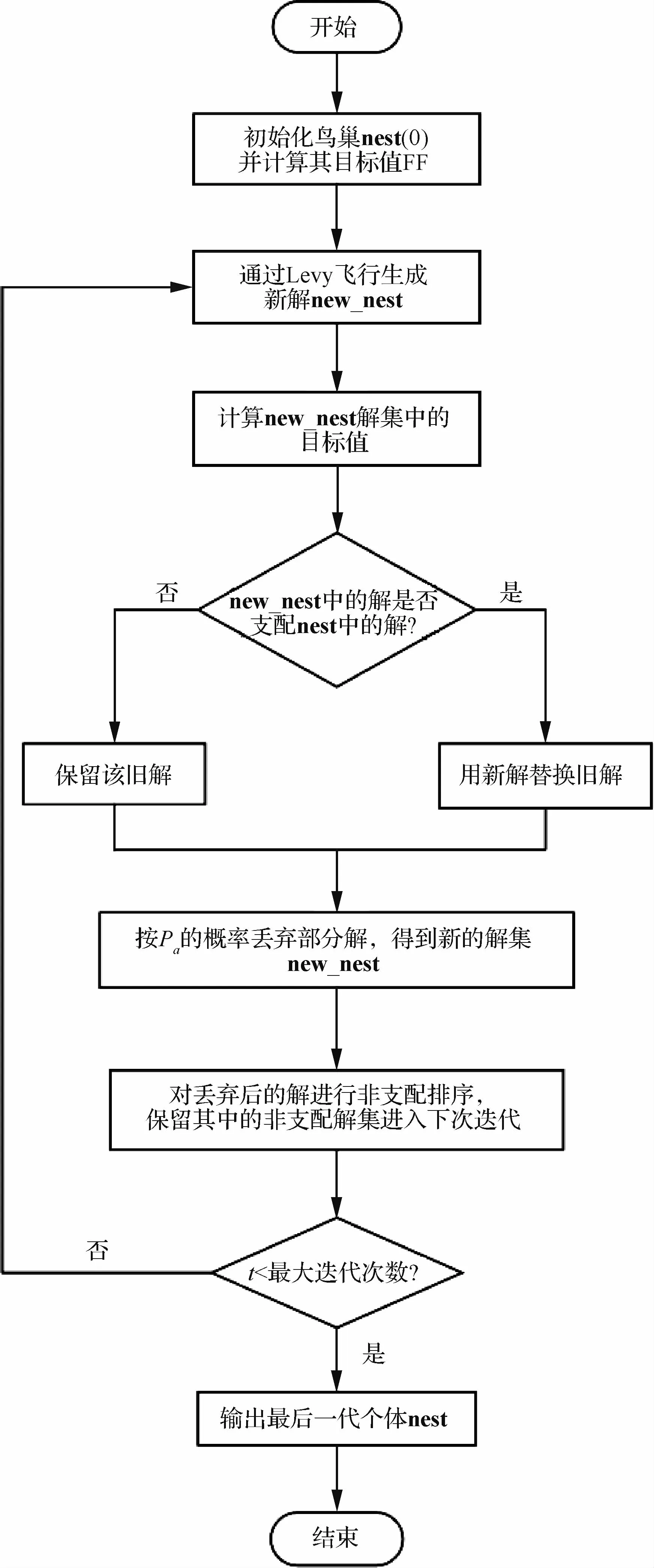
圖1 MOCS算法流程圖Fig.1 Flow diagram of MOCS algorithm

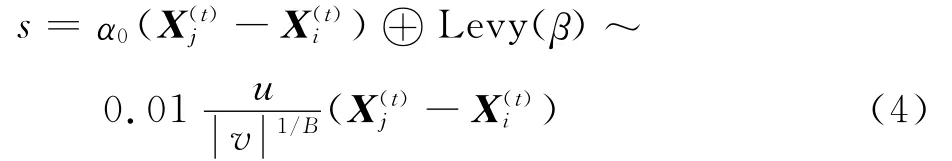
式中：u和v都服從正態分布：

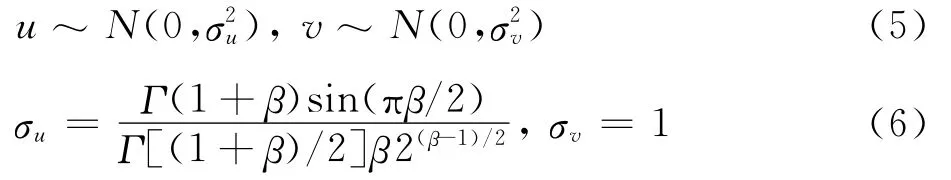
Algorithm 1：MOCS algorithm［13］1Initialize objective functions f1（x），f2（x），…，fK（x），x ＝［x1，x2，…，xd］T 2Generate an initial population of n host nest xiand each 3with keggs 4while（t＜MaxGeneration）5 Get a cuckoo（say i）randomly by levy flights 6 Evaluate and check if it is Pareto optimal 7 Choose a nest among n （say j）randomly 8 Evaluate ksolutions for nest j 9 if new solutions of nest j dominate those of nest i 10 Replace nest i by the new solution set of nest j 11 end 12 Abandon a fraction（Pa）of worse nests 13 Keep the best solutions 14 Sort and find the current pareto optimal solutions 15 end 16 Post process results and visualization

對比求解單目標的CS算法［8］和求解多目標的MOCS算法［13］，可以看出MOCS算法是直接從CS算法推廣而來的，其主要區別在于單目標優化算法中一次產一個鳥蛋（對應一個目標）更改為一次產多個鳥蛋（對應多個目標），單目標優化算法中以較小的目標值作為較好的解，多目標優化算法中將可以完全支配其他解的解作為較好的解。這一簡單的更改雖然實現了求解多目標優化問題的功能，但存在以下不足：① 單目標優化最終結果只有一個最優解，在迭代過程中，若新解比舊解適應度高則替代舊解，這將驅動算法始終朝向更優的解收斂。因此，對比新解與舊解的優劣性時只有兩種情況：新解優于舊解或劣于舊解。而多目標優化問題最終求解的是一個Pareto解集，也就是存在多個互相妥協的解。因此，新解與舊解對比優劣性時應該有3種情況：新解支配舊解、舊解支配新解、兩兩互不支配。MOCS算法直接來源于單目標算法，并未考慮到第3種情況。② 單目標優化問題求解的是一個最優解，故CS算法在迭代過程中僅考慮新解與舊解之間的優劣性，而不需考慮不同個體之間的優劣性，而多目標優化問題求解的是一個應該盡量分布均勻的解集，因此，對于多目標優化，群體之間的優劣性與均勻性應當統一考慮，也就是除了應該考慮新解與舊解的支配關系，還應該考慮個體之間的相互支配關系。MOCS算法直接來源于單目標CS算法，并未考慮到這點。③ 在單目標CS算法中，一個解在隨機丟棄之前，已經保存了當前個體中目標值最小的個體，這保證了最優解不會被丟棄，而推廣得到的MOCS算法并沒有對適應度高的個體進行保存，這樣在隨機丟棄中，無論解的適應度有多高，都會以Pa的概率被丟棄，導致把較好的解丟棄掉，影響到最終的優化結果。對于以上不足，為了使其更好地應用于氣動優化問題中，需要對原始的MOCS算法進行改進。

2 改進的多目標布谷鳥搜索算法

鑒于布谷鳥搜索算法在單目標優化問題中的優秀表現（算法中采用的Levy飛行機制提高了全局搜索效率［15］），但在直接推廣到多目標算法中存在的一些不足，本文提出一系列改進措施，以期充分發揮布谷鳥搜索算法在多目標氣動優化設計中的性能。

本文從增強解的適應度、改進布谷鳥局部隨機游走策略、改進自適應丟棄頻率、增加檔案的管理來獲得更多Pareto最優解這幾個方面對MOCS算法進行改進，進而提出了改進的多目標布谷鳥搜索（IMOCS）算法。

2.1 算法改進措施

MOCS算法以支配關系來提高解的適應度，當新解支配舊解時，認為新解的適應度高于舊解，從而用新解替換掉舊解。這樣會存在一個問題，就是存在支配關系的解占少數，所以替換的發生次數很少，導致算法的收斂速度過慢。

借鑒NSGA-Ⅱ算法的優勢，本文在 MOCS算法中引入快速非支配排序［16］的方法，使得解的更新加快，算法更容易收斂。

多目標優化算法理想的優化結果是：① 所有的解均在優化問題的全局Pareto最優解集中；② 所有的解均勻分布在整個Pareto前沿上，即解的收斂性和均勻性是評價優化結果的兩個主要指標。然而使用非支配排序對解進行適應度評估，可提高解的收斂性卻無法保證解的分布均勻性，因此，為提高解的均勻性，本文引入擁擠距離［16］方法。對于兩個目標的優化問題，一個解的擁擠距離的大小由與這個解相鄰的兩個解構成的長方形的長和寬之和來度量，如圖2所示，圖中f1表示個體第1個目標值，f2表示個體第2個目標值。

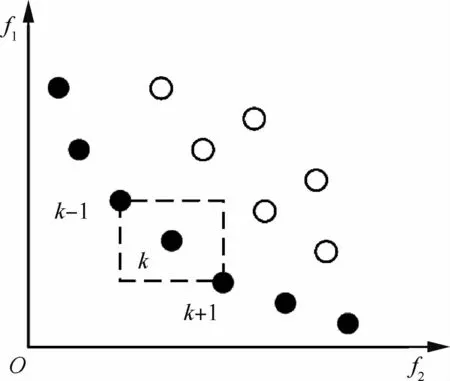
圖2 擁擠距離Fig.2 Crowding distance

在MOCS算法中，隨機游走策略是根據解的相似性來決定搜索步長的［17］，其表達式為

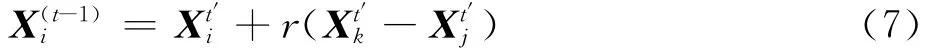
式中：Xt′k和Xt′j為從種群中隨機選取的兩個解；r為在［0，1］區間上均勻分布的隨機數。

這里存在一個丟棄概率，首先產生一個0-1分布的隨機數，當產生的這個隨機數小于丟棄概率，則該解會被丟棄，新的解由式（7）來生成。解的移動步長由兩部分組成，一個是生成的隨機數r，一個是向量差分運算Xt′k－Xt′j。但這樣進行解的更新存在一個問題，新解的生成是隨機的，解的更新沒有方向性。

文獻［17］在MOCS算法的局部搜索中引入了隨機數r和1－r，它使得解的更新方向更加隨機，從而增強了子代個體的多樣性。故本文在MOCS算法局部搜索的差分因子中加入隨機數r和1－r，于是式（7）修改為

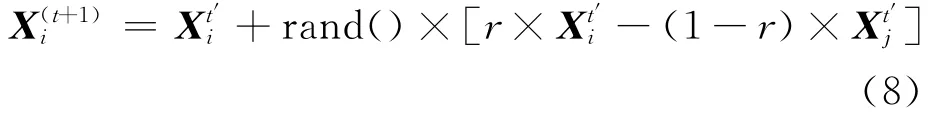
式中：rand為在［0，1］區間上均勻分布的隨機數。

MOCS算法在局部搜索步驟中，無論一個解的適應度有多高，它都有可能被丟掉，并且丟棄頻率的高低也會影響到解更新的步長，當找到一個適應度很高的解時，更傾向于在它周圍很小的范圍內進行尋找。所以本文對丟棄概率進行改進如下：

1）將產生的新解和舊解合并進行適應度從大到小的排序。

2）將丟棄概率Pa設定為動態可調節：Pa∈［Pa，min，Pa，max］。

3）生成從Pa，min～Pa，max等間距并且長度與解的個數相同的數組，適應度最高的解采用最低的丟棄概率，適應度最低的解采用最高的丟棄概率。

當算法一步步進行迭代之后，迭代次數越高，則個體中Pareto最優解的個數越多，根據上述思想，需要將丟棄概率Pa整體減小，來對最優解的附近進行搜索（局部搜索）。

4）將丟棄概率的最大值和最小值隨著迭代次數的增加進行線性變化，可以由式（9）和式（10）來實現。

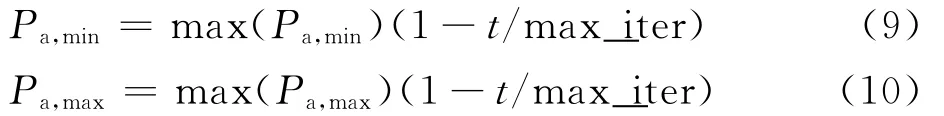
式中：t為當前迭代的次數；max＿iter為最大迭代次數。

當使用優化算法進行多目標優化時，希望優化算法得到的個體可以等間距地分布在整個Pareto前沿上。前面分析到MOCS算法需要有一個解的存檔過程，將生成的解歸入檔案中，以供挑選。因此，這個存檔也需要一個合理的檔案刪除與保留機制。本文參考基于共享半徑的小生境技術［18］，共享半徑的值由圖3設定，圖中σshare表示共享半徑大小。將落在共享半徑內的個體進行剔除，如果兩個解之間的間距小于共享半徑，則舍棄；兩個解之間的間距大于共享半徑則保留。這樣檔案管理機制有以下3種功能：① 刪除掉檔案中的重復個體；② 刪掉檔案中相距較近的個體；③ 保留非支配解。IMOCS算法的偽代碼見Algorithm 2。

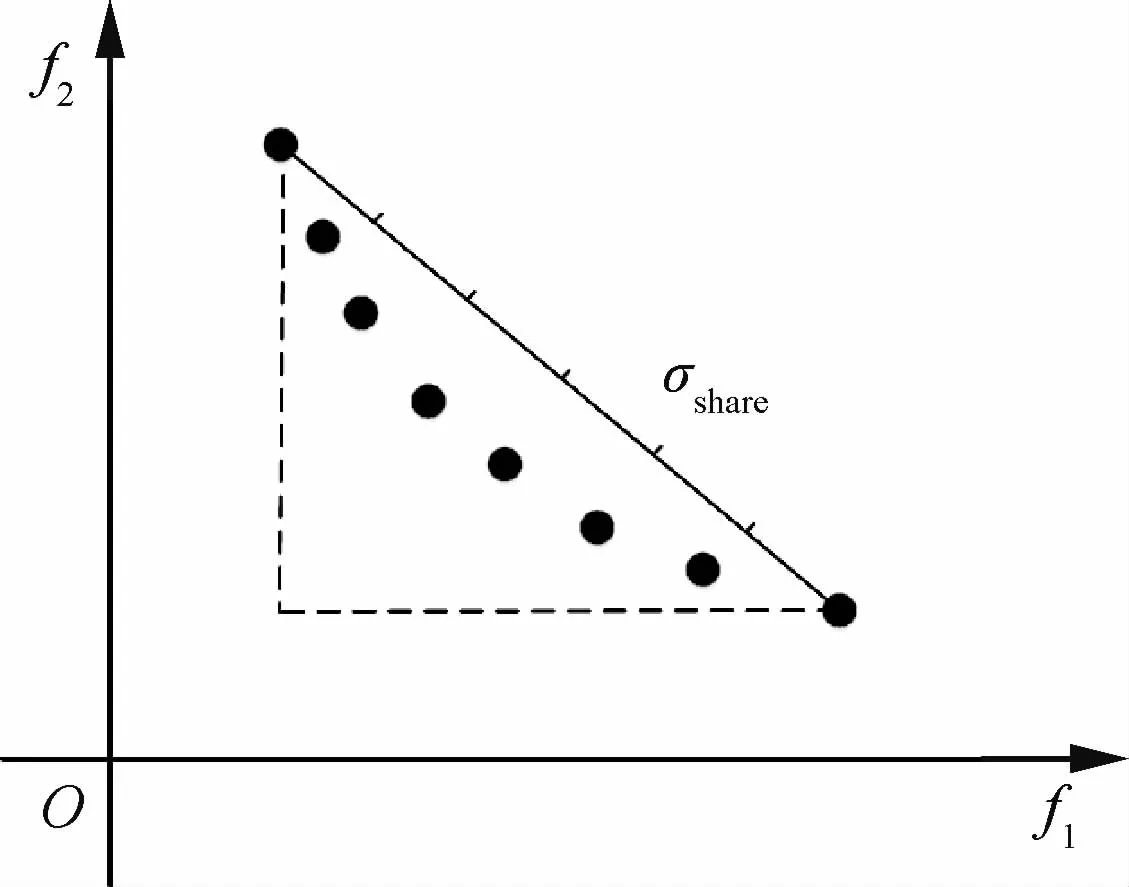
圖3 自適應共享半徑Fig.3 Adaptive sharing radius

orithm 1Initialize objective functions f1（x），f2（x），…，fk（x），x ＝［x1，x2，…，xd］Algorithm 2：IMOCS alg T 2Generate an initial nest of nindividuals xiand each with 3 keggs 4 while t＜MaxGeneration 5 Get new nest of nindividuals randomly by Levy flights 6 Evaluate fitness of all individuals of new nest 7 Combine nest and new nest then conduct non-dominated

8 sorting to all 2nindividuals.9 Evaluate crowding distance and rank from height to low 10 Replace nest by first nindividuals 11 Abandon a fraction（Pa）of worse nest and obtain new 12 nest by formula 8 13 Combine nest and new nest then conduct non-dominated 14 sorting to all 2nindividuals 15 Evaluate crowding distance and rank from height to low 16 Replace nest by first nindividuals and keep nest into 17 next iteration 18 Deposit all nindividuals of nest in archive 19 if size of archive＞max＿archive 20 Delete duplicate individuals in the archive 21 Delete individuals in the archive that are closer 22 end 23 end 24Output all individuals of archive as optimization result and 25visualization

2.2 算法步驟

根據以上改進措施，給出改進的多目標布谷鳥搜素算法的實現步驟。

步驟1 設定算法相關參數。

步驟2 初始化鳥巢群nest，計算其目標值。

步驟3 通過改進的Levy飛行生成新的鳥巢群new＿nest。

步驟4 計算new＿nest中個體的目標值。

步驟5 將新解和舊解進行非支配分層排序；然后按分層的結果，分層計算擁擠距離；最后按層數和擁擠距離兩個指標進行排序，層數為一級指標，擁擠距離為二級指標。

步驟6 取前n個排序結果，替換掉nest中的個體。

步驟7 將這n個個體存入檔案archive中。

步驟8 按丟棄頻率Pa丟棄部分解，并利用改進的局部游走生成新的鳥巢new＿nest。

步驟9 重復運行步驟4～步驟8。

步驟10 將排序之后的前n個個體存檔案。

步驟11 檢查檔案中個體是否超過限定的最大容量A＿max，若超過了A＿max，則進行檔案的管理；否則進行下一步。

步驟12 判斷當前迭代次數是否大于最大迭代次數max＿iter，若小于最大迭代次數max＿iter，程序則轉向步驟3；若大于最大迭代次數max＿iter，則停止迭代，輸出結果。

步驟13 對計算結果進行分析處理。

2.3 仿真測試

為了驗證本文提出的IMOCS算法的有效性，采用4個典型的測試函數對IMOCS算法進行仿真測試，并與改進前的MOCS算法和NSGA-Ⅱ算法進行比較分析。對于IMOCS算法和MOCS算法，仿真測試均取鳥巢數為50，迭代次數為100（由于每次迭代需計算2次群體的目標值，故總的目標函數計算次數為10000）。對于NSGA-Ⅱ算法，群體個數取100，迭代次數100，以保證3種算法總的目標計算次數相同。

1）ZDT1測試函數

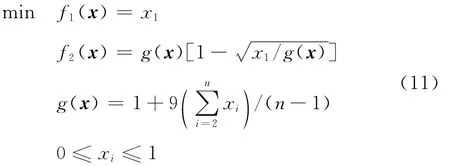
變量個數n取30，ZDT1測試函數擁有連續的凹狀Pareto前沿。

2）ZDT2測試函數

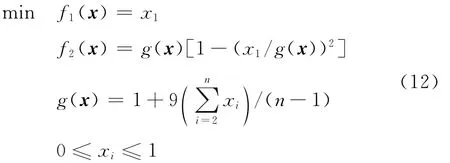
變量個數n為30，ZDT2測試函數擁有連續的凸狀Pareto前沿。

3）ZDT3測試函數

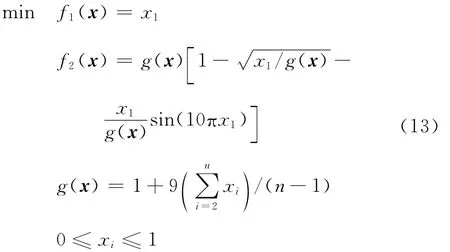
變量個數n取30，ZDT3測試函數Pareto前沿是間斷的。

4）ZDT6測試函數

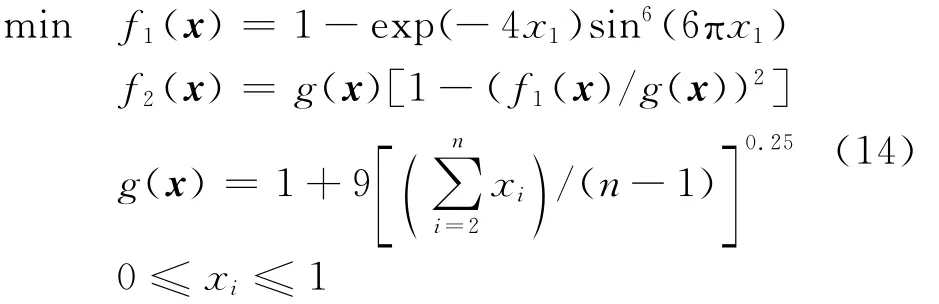
對于ZDT6測試函數，它搜索空間的非均勻性會帶來兩種優化困難：①Pareto最優解在全局Pareto前沿上是非均勻分布的（前沿集中于f1（x）＝1的解）；② 接近于Pareto全局最優解的多樣性最低，遠離前沿解的多樣性又很高［19］。

使用 MOCS算法和 NSGA-Ⅱ算法與IMOCS算法對測試函數算例進行仿真，算法參數設置如表1所示，優化結果對比如圖4所示。NSGA-Ⅱ算法需要設置交叉概率Pc、變異概率Pm、交叉分布指數eta＿c、變異分布指數eta＿m。

表1 算法參數設置Table 1 Parameter settings of algorithms

從4個函數算例優化結果對比可以得到，IMOCS得到的Pareto解集與函數算例真實的Pareto前沿更加接近，對于4個函數算例，IMOCS算法優化結果均好于NSGA-Ⅱ和MOCS算法。注意，圖中MOCS算法表現欠佳的原因是受限于迭代次數，增加迭代次數后表現會更好。

優化過程中誤差隨迭代次數的變化如圖5所示。可以看出，對于所有測試函數算例，IMOCS算法的收斂速度相較于NSGA-Ⅱ和MOCS算法均更快，尤其是對于具有非均勻分布且多樣性較低的全局最優解的ZDT6函數，相較于NSGA-Ⅱ和MOCS算法優勢更為明顯。

評價多目標優化算法的性能指標主要有解的收斂性和多樣性［17］。

1）收斂性指標 用來評價算法的收斂性，它是采用每個個體距離真實Pareto前沿的平均距離（GD）作為算法收斂性的指標，其定義為

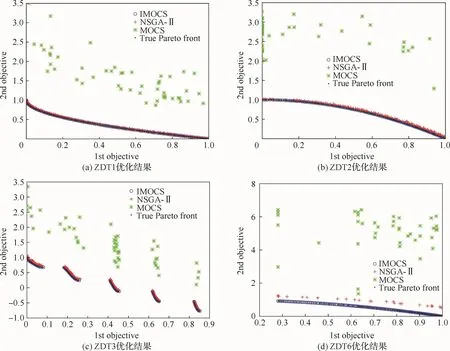
圖4 測試函數優化結果對比Fig.4 Comparison of test function optimization results

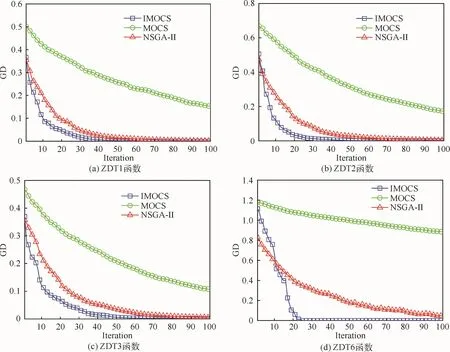
圖5 收斂速度比較Fig.5 Comparison of convergence speeds

2）多樣性指標 用來評價算法的解的分布多樣性。個體間距（SP）的定義為

為了降低算法的隨機性對結果的影響，分別采用IMOCS算法、NSGA-Ⅱ和MOCS算法對上述數值算例重復優化30次，計算所得的Pareto最優解的收斂性指標和多樣性指標的平均值與標準差如表2所示。從表中可以看出，對于4種測試函數，IMOCS算法的平均GD值比NSGA-Ⅱ和MOCS算法小，且大幅度優于MOCS算法，表明IMOCS算法的收斂精度比NSGA-Ⅱ和MOCS算法收斂精度更高，IMOCS算法的平均SP值比NSGA-Ⅱ和MOCS算法小，說明IMOCS算法得到的Pareto解分布更均勻。IMOCS算法的GD和SP值的方差更小，說明IMOCS相較于其他兩種算法更加穩定。仿真結果表明改進后的算法性能提升很大，并優于目前主流的NSGA-Ⅱ算法。

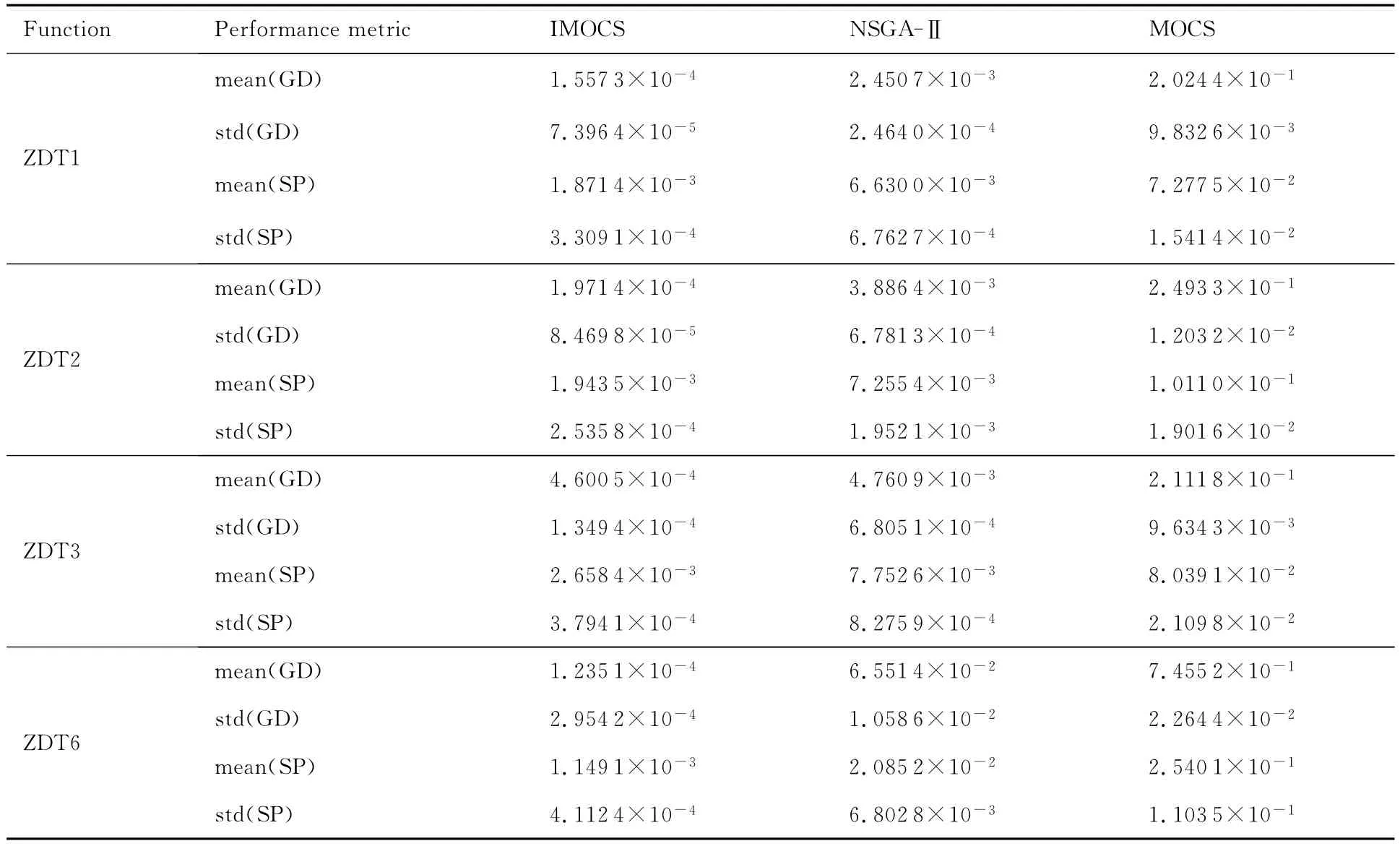
表2 不同算法性能比較Table 2 Comparison of performance of different algorithms

3 翼型Pareto多目標優化設計

在飛行器設計中，翼型設計是很關鍵的一步。在測試函數的優化中，IMOCS算法表現出了很好的收斂性和解的分布性。本節將IMOCS算法引入到實際的翼型多目標優化設計中，測試IMOCS算法在氣動優化設計中的表現。

3.1 翼型幾何外形參數化

翼型參數化是氣動優化中非常重要的一步，翼型的參數化擬合精度決定了設計出的翼型的可靠性，國內外研究了很多翼型參數方法，例如：形狀類別函數變換（CST）方法［20］、Hicks-Henne型函數法［21］、Parsec 方法［22］、NURBS（Non-Uniform Rational B-Splines）方法［23］、Bezier 方法［24］、FFD 變形技術［25］等。其中在翼型上使用比較廣泛的為CST方法和Hicks-Henne型函數法。本文采用CST參數化方法，使用10個設計變量來描述翼型的幾何外形。關于CST方法的具體描述可參考文獻［26］。

3.2 網格自動生成技術

本節所采用的翼型網格自動生成程序可以通過求解橢圓型方程的方法和無限插值的方法生成“C”型和“O”型結構網格，網格第1層高度為1×10－5m，遠場取20倍弦長。網格單元數為320×64，使用“C”型網格對求解翼型繞流，圖6給出了所使用的“C”型計算網格的全貌和網格局部放大圖。

圖6 計算網格Fig.6 Mesh for computation

3.3 流場數值計算

本文采用求解雷諾平均Navier-Stokes方程來進行翼型的氣動性能計算。流場計算采用隱式求解、加入預處理、多重網格等數值模擬技術。空間離散格式為Jameson中心離散格式，湍流模型采用Spalart-Allmaras湍流模型。

為了驗證對RAE2822翼型流場數值求解方法的有效性，將數值求解的壓力系數Cp結果與其試驗值［27］對比，如圖7所示，圖中Ma為馬赫數，α為迎角，Re為雷諾數。

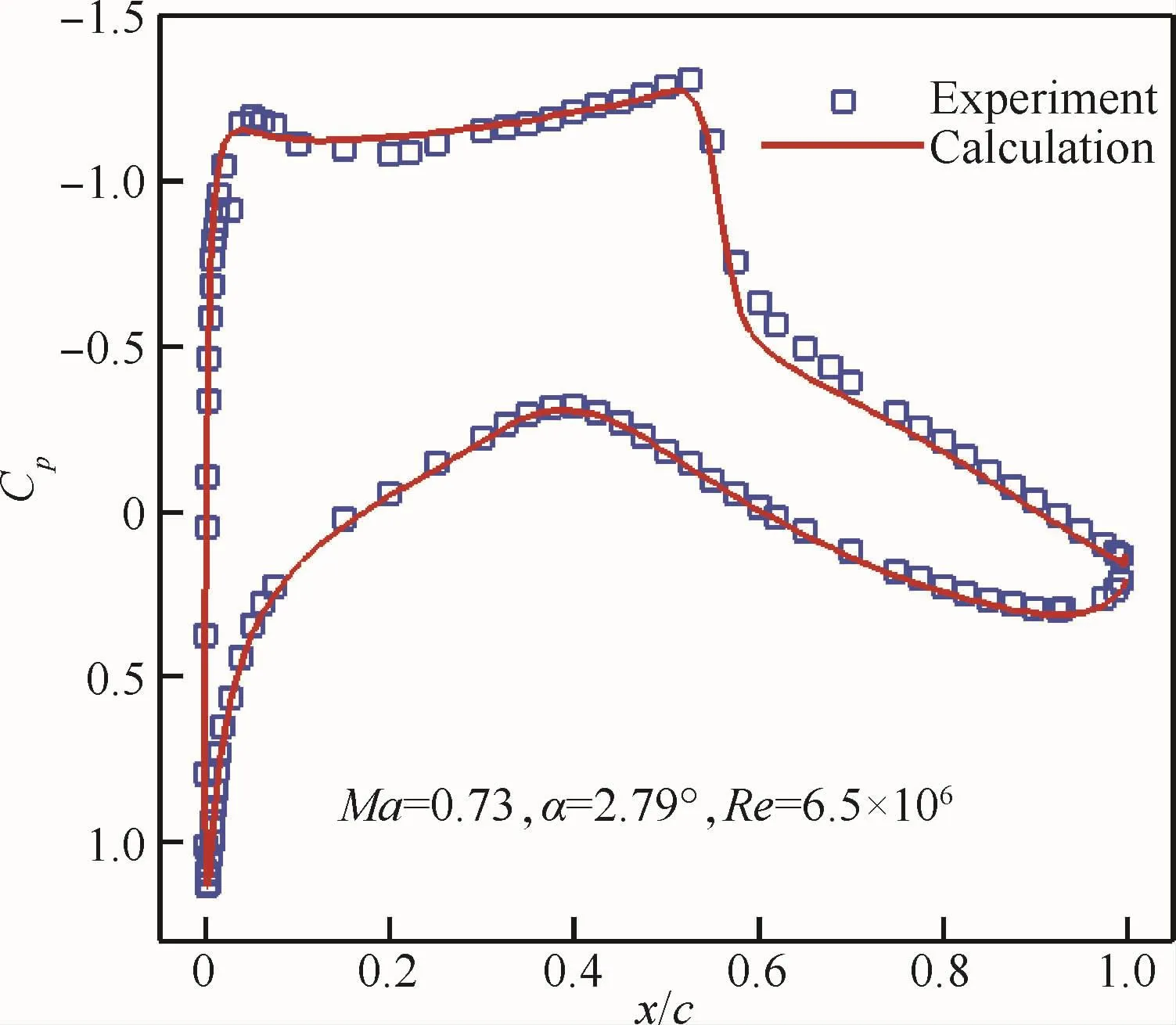
圖7 計算與試驗的壓力系數分布對比Fig.7 Comparison of pressure coefficient distribution between calculation and experiment

3.4 翼型Pareto多目標優化設計

本文選取兩種狀態的升阻比作為優化目標。第1個設計狀態為：Ma＝0.75，Re＝6×106，α＝2.31°；第2個設計狀態為：Ma＝0.6，Re＝6.5×106，α＝2.31°。優化目標為：在這兩種工作狀態下翼型的升阻比最大。該多目標優化問題可描述為

式中：CL為升力系數；CD為阻力系數。

采用IMOCS算法進行優化，設置鳥巢數為50，迭代次數為100。IMOCS算法共得到了64個Pareto最優解，如圖8所示，圖中五角星代表基準翼型的氣動性能。本文從中選取3個Pareto解進行翼型氣動分析。

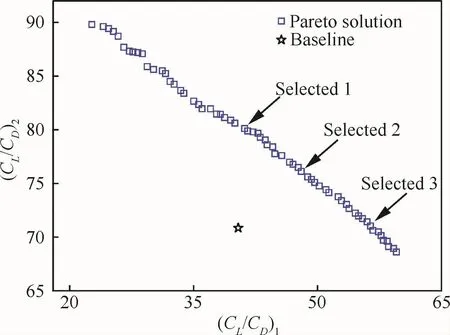
圖8 IMOCS算法的優化結果Fig.8 Optimization results of IMOCS algorithm

表3給出了翼型優化前后兩種狀態下的氣動特性對比。優化翼型1在狀態1中，相較于基準翼型升阻比基本不變，而在狀態2中，升阻比從70.86提升到80.106 8，提升了13.05%，該翼型在保證其狀態1中升阻比不損失的情況下大幅提高了狀態2下的升阻比。優化翼型2在狀態1中，相較于基準翼型升阻比從40.39提升到48.023 5，提升了18.90%，而在狀態2中，升阻比從70.86提升到了76.123 5，提升了7.43%，該翼型折中考慮了狀態1和狀態2中升阻比的提升。優化翼型3在狀態1中相較于基準翼型升阻比從40.39提升到56.413 9，提升了39.67%，而在狀態2中，升阻比基本不變。

優化前后翼型幾何外形對比如圖9所示，圖10給出了優化前后翼型在兩種狀態下的壓力系數Cp分布，優化翼型1相較于基準翼型激波強度基本不變，優化翼型2激波強度稍有減弱，優化翼型3激波已基本消除；對于狀態2，優化翼型1的升力系數比基準翼型有較大提升。這與表3中的結果相符，即對于優化翼型2和3，狀態1的升阻比提升主要是由于激波減弱、阻力降低；而對于狀態2，優化翼型1的升阻比提升主要是升力提升帶來的。

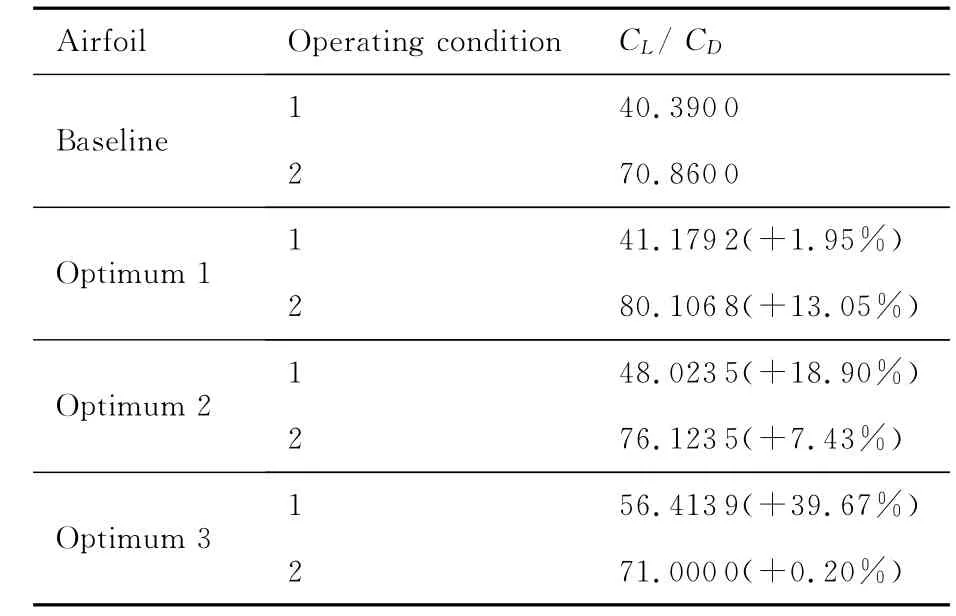
表3 優化前后氣動性能對比Table 3 Comparison of aerodynamic performance between baseline and optimized airfoils

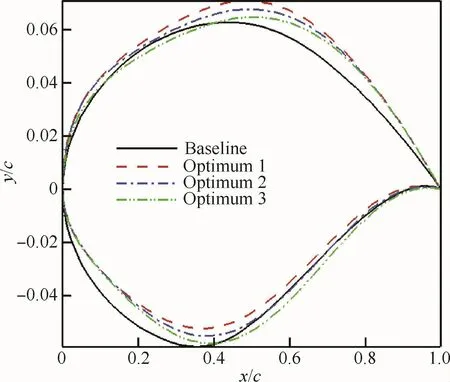
圖9 優化前后翼型幾何形狀對比Fig.9 Comparison of shape between baseline and optimized airfoils

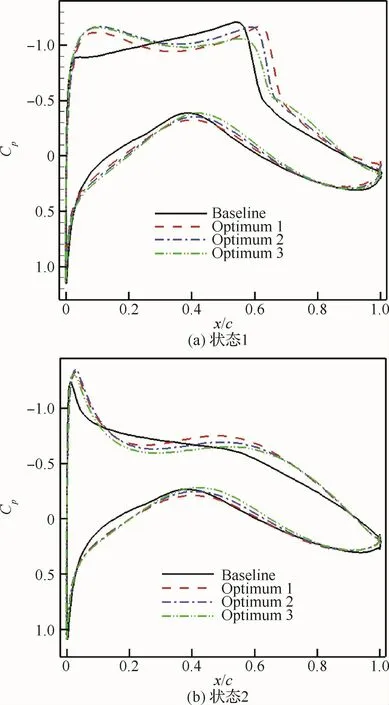
圖10 兩個狀態下優化前后翼型壓力系數分布對比Fig.10 Pressure coefficient distribution comparison of baseline and optimized airfoils under Conditions 1and 2

選取的Pareto解不同，所得到的優化翼型在狀態1和狀態2中氣動特性提升的幅度不同，設計者可以針對具體問題來選取合適的Pareto解。

3.5 3種算法優化結果比較

3種算法的參數設置與測試函數仿真算例參數設置相同，優化結果比較如圖11所示。

從圖11可知，流場計算次數相同的時候，IMCOS算法與NSGA-II均有比較好的收斂效果，而MOCS算法還未收斂，說明MOCS算法不適合直接用于工程優化問題，為了進一步比較IMOCS算法和NSGA-Ⅱ用于解決氣動優化問題的性能，在迭代過程中選取第20代、第40代、第60代、第80代計算結果進行比較，如圖12所示。

根據不同迭代次數IMOCS算法和NSGA-Ⅱ算法的優化結果對比，可以得出，對于氣動優化問題，IMOCS算法收斂速度明顯快于NSGA-Ⅱ算法，這也說明對于復雜的工程優化問題，IMOCS算法可以使用更少的迭代次數來獲得優化問題的Pareto最優解集。

4 結 論

1）本文針對原始的多目標布谷鳥搜索算法的不足，分別從增強解的適應度，改進布谷鳥局部隨機游走策略，改進自適應丟棄頻率，增加檔案的管理機制4個方面對MOCS算法進行改進，得到了性能更優秀的IMOCS算法。使用測試函數對IMOCS、MOCS和NSGA-Ⅱ算法的仿真測試結果表明，改進后的IMOCS算法大幅度提升了算法的收斂速度和收斂精度。并且，IMOCS算法相較于發展成熟的NSGA-Ⅱ算法擁有更強的全局搜索能力、更快的收斂速度和更高的收斂精度，同時，所得到的Pareto解分布更加均勻。

2）將IMOCS算法應用于翼型的Pareto多目標氣動優化設計中，將兩個不同狀態下的升阻比作為優化目標，IMOCS算法經過10 000次的流場計算，共獲得了64個不同的翼型，設計者可以根據自己的偏好來選取合適的優化翼型。算法在進行相同次數的流場計算后，IMOCS算法相較于原始的MOCS算法具有更高的收斂精度。通過不同迭代次數下IMOCS算法和NSGA-Ⅱ算法優化結果的對比，得到IMOCS算法收斂速度明顯快于NSGA-Ⅱ算法，說明IMOCS算法相較于目前主流的NSGA-Ⅱ算法可以更快地解決復雜的氣動優化問題。

3）在測試函數的仿真中，IMOCS算法的收斂速度和收斂精度優于NSGA-II算法，相信它在工程優化領域中是一種極具潛力的優化算法。在氣動優化中，可以考慮將其與其他算法相結合，進而將其應用于解決更復雜的實際問題。

當前IMOCS算法僅應用于兩個目標的多目標優化問題，下一步將研究其對3個及以上目標問題的適用性。