三次均勻B樣條在求解軌道曲率中的應用

蔡文豪 黃 玲 高 聰

（廣東省建筑科學研究院集團股份有限公司，廣東 廣州 510500）

隨著大型城市的經濟穩步增長和科技高速發展，越來越多的人口流向了這些大型城市，擁擠的人口給城市交通帶了巨大的壓力和挑戰。城市軌道交通成為應對這一挑戰的首選。城市軌道交通是特大型隱蔽性的系統工程，一項工程投資將達上百億，涉及十幾個專業，地鐵施工具有難度大、復雜程度高、項目周期長，周邊環境影響大、風險等級高的特點。為了充分保障城市軌道交通完成每天安全運送數百萬人次的任務，其質量控制也是尤為嚴苛，這其中之一就是對地鐵隧道的各項參數進行檢測。

運營期間的地鐵隧道關注重點之一在于其軌道的位移監測。地鐵隧道的沉降控制值、沉降速率控制值均已在相關規范中作出規定。為了保障列車行駛安全，《上海市地鐵沿線建筑施工保護地鐵技術管理暫行規定》規定了地鐵軌道的最小曲率半徑不得小于15 000 m，這一限值在工程界被廣泛采用[1-3]。對于具體的隧道區間，通常只按照指定的間隔監測其沉降值，如何根據這一系列離散的沉降監測值求整個隧道的曲率值是一個重要的問題。文章將采用三次均勻B樣條曲線擬合的方法進行求解。

1 三次均勻B樣條

在數值分析領域中，B樣條或基本樣條是這樣的樣條函數——其對給定的自由度、平滑度和域區劃分具有最小的支集（support）。給定自由度的任何樣條函數都可以表示為該自由度的B樣條的線性組合[4]。基本B樣條具有彼此等距的結點，可很好地應用于曲線擬合和數值差分中。

本質上，n階樣條是一個變量為x的n-1階分段多項式函數。各分段多項式“接頭”處的變量值稱之為節點，用…,t0, t1, t2, …表示，并且將這些節點在數值上按照非遞減順序排列。若上述節點各異時，多項式部分的前n-1個導數在每個節點連續；若上述節點中有個節點重合，則只有樣條的前n-r個導數在該節點連續。此外，若上述節點各異并且等間距，稱之為均勻樣條，否則稱之為非均勻樣條。本研究是基于均勻樣條展開的。

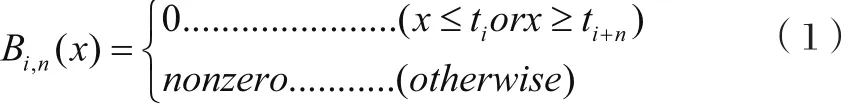
或者，可以通過Cox-de Boor遞歸公式[5]來構造B樣條。對于給定的結點序列…, t0, t1, t2, …，一階B樣條可以如此定義：

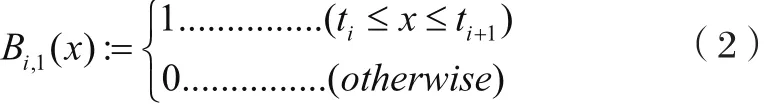
而更高階的B樣條通過如下遞歸公式定義：

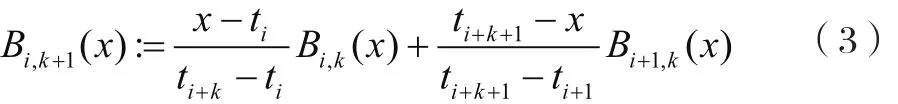
2 曲率的求解

按照上述方式可根據原始監測數據進行三次均勻B樣條擬合，從而求出整個隧道區間的沉降曲線，理論上，該曲線是一條二階連續可導的平滑曲線。由于計算過程均采用計算機編程的方式完成，實際上最終的曲線由一系列間距很小的離散點表示。沉降后的軌道曲率正是基于這一系列離散的光滑散點，并采用數值計算的方式完成。筆者將介紹在曲率求解中遇到的問題，以啟發讀者。

曲線的曲率（curvature）就是針對曲線上某個點的切線方向角對弧長的轉動率，通過微分來定義，表明曲線偏離直線的程度（如圖1所示），數學上表明曲線在某一點的彎曲程度的數值[6]。曲率的另一個定義是，在曲線任一點作一個與該曲線相切的圓（密切圓），該圓半徑的倒數即為該曲線在該點的曲率，而該圓的半徑則稱之為該點處的曲率半徑，如圖2所示。

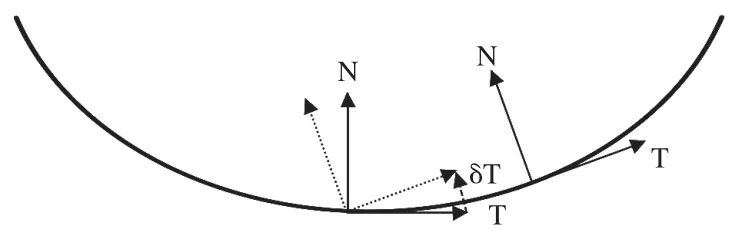
圖1 曲率的數學定義

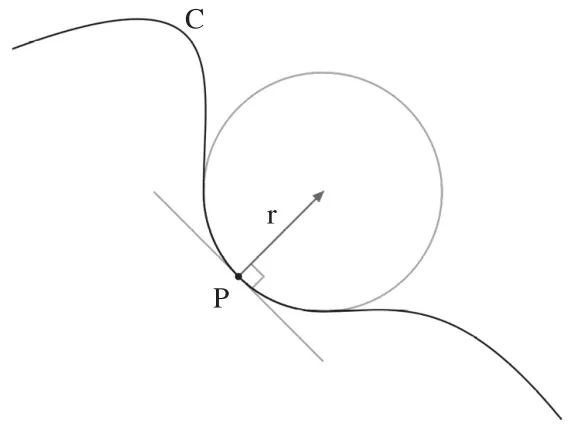
圖2 曲率與密切圓的關系

對于曲率的求解，最先想到的就是定義法。即對于任何一個光滑曲線 y=f(x)，其曲率可根據定義推導出如下公式：

上式中關于一階導數和二階導數的求解，可以對曲線橫坐標做盡可能小的細分，并采用差分近似微分的方法（即在圖像上表現出割線近似代替切線的方法）來進行數值計算。即第j點的一階導數可由如下差分格式求得：

課堂1：老師聲音清晰，但是緊張，后稍好。準備教學材料充分，講故事學習單詞，較好，但是節奏緩慢。問題太難，提示較少，沒有介紹強調具體的事例或語言點，給學生做筆記。(2006年10月9日)

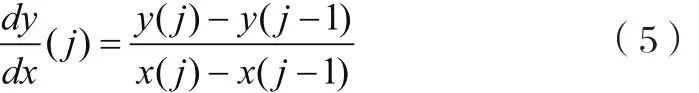
通常，在計算過程中取均勻步長，即h=x( j)-x( j-1)為一定值，則上式為：

同理，即第j點的二階導數可由如下差分格式求得：

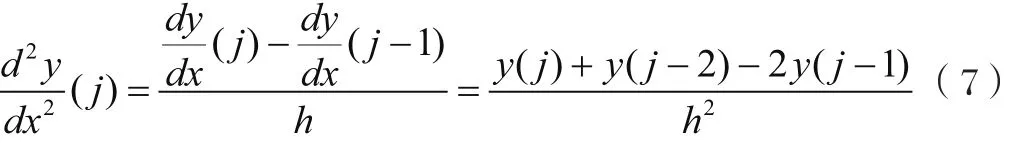
需要注意的是，對于討論的軌道曲率半徑的求解問題，由于所討論區間隧道的長度方向量級通常都在數十米至數百米之間，而隧道的沉降都是毫米量級，因此上述差分數值都非常小，再加之差分格式穩定性問題[7]，導致用曲率公式方法求解軌道曲率的結果很不理想，極易出現數值震蕩、發散、無法計算結果等問題。因此，對于軌道曲率的求解需要另辟蹊徑。

根據隧道沉降量相對于長度方向極小的特點以及數值計算過程對里程區間縱向充分劃分的前提條件，可采用三點定圓法近似求解軌道曲率[8]。其求解過程如下。

對于軌道曲線上的任意三點A，B，C，總能確定一個外接圓（若這三點在一條直線上，則可認為該外接圓半徑無窮大），若這三點無限接近，則該外接圓與軌道曲線相切，此時外接圓的半徑的倒數即為曲線在該點的曲率，如圖3所示。正如前文所述，軌道沉降量相對于軌道縱向方向極小，且里程區間縱向充分劃分，即A，B，C三點充分接近彼此。這時可由A，B，C三點確定的外接圓來近似替代曲線的密切圓，換言之，該圓的半徑倒數即為要求的曲率。

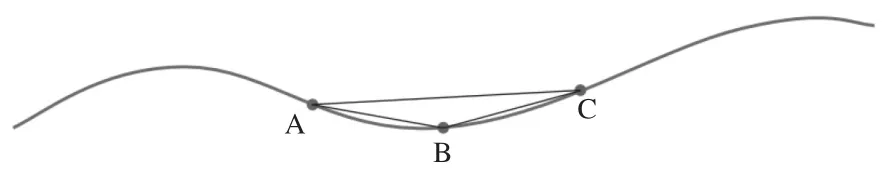
圖3 三點定圓法求取率示意圖

上述三角形ABC的三邊長度分別為BC=a，CA=b，AB=c則根據正弦公式很容易推出三角形外接圓半徑的表達式，其倒數即為曲率：

注意到在求解軌道曲率過程中，上述三角形ABC實際上是一個“極狹長”的鈍角三角形，換言之，a+c-b≈0，甚至對于平直的軌道段有a+c-b=0。因此，曲率的求解變成了一個如何求“極狹長”的鈍角三角形面積的問題。

思路一：海倫公式法。記三角形的半周長為p=(a+b+c)/2，則三角形面積公式為：

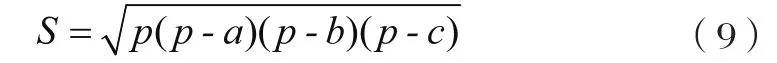
思路二：行列式法。設A，B，C三點的坐標分別為(x1,y1)，(x2, y2)，(x3, y3)，則三角形面積可由頂點坐標表示的行列式求得（式中雙豎線表示行列式求絕對值）：

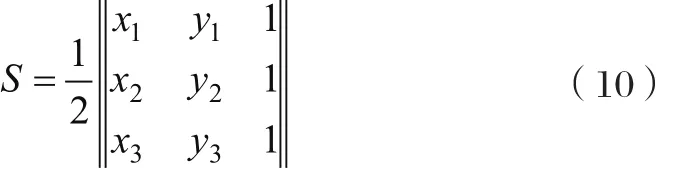
由于海倫公式中p-b≈0，為了避免計算中出現“大數吃小數”的數值現象，因此用三頂點的坐標建立行列式的方法求“極狹長”的鈍角三角形的面積。

綜上所述，一共提出了三種求解曲率的方法。由于軌道沉降值相對于其縱向里程量級特別小這一特殊原因，為了避免數值計算過程中的“大數吃小數”和其他數值發散現象，采用了三點定圓法結合坐標頂點行列式求三角形面積方法求解軌道曲率。這種做法的最主要優點是在數值計算過程中避免開根號的計算，從而有效避免數值發散。

3 應用

案例一：某地鐵線路的某一區間為明挖段，隧道主要位于強風化泥質粉砂巖、中風化泥質粉砂巖、微風化泥質粉砂巖中。該區間位于珠江三角洲中西部，地形平坦，勘察期間測得鉆孔地下水位埋深一般0.7～2.9 m，地下水受季節暴雨和河水水位的影響。該區間左線約3.26 km，監測點間距約40 m；右線約2.34 km，監測點間距約60 m。其最后一次沉降監測值如圖4中散點所示，根據散點進行三次均勻B樣條擬合得到整個區間的沉降曲線，如圖4中實線所示。

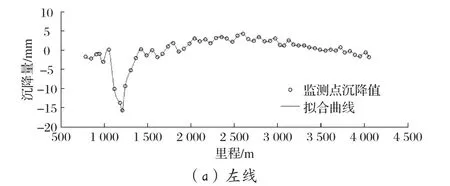
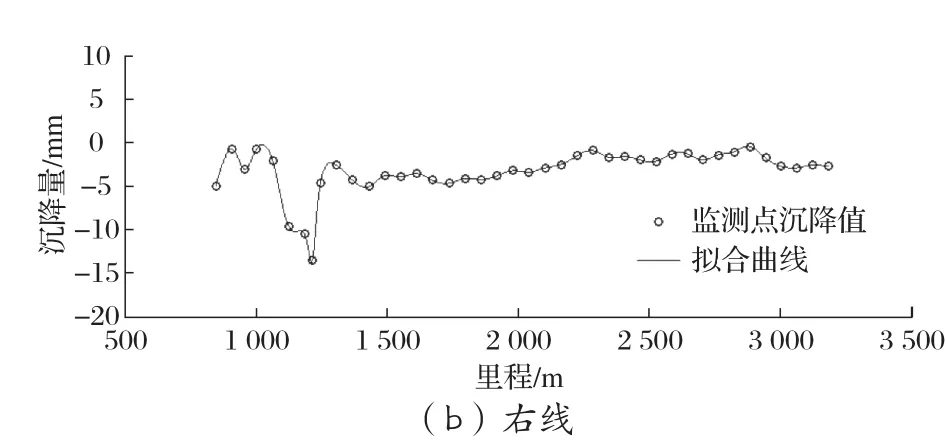
圖4 案例一的監測點沉降值和擬合曲線

采用前文所述的三點定圓法結合坐標頂點行列式求三角形面積方法求解軌道曲率，如圖5所示。注意，為了清晰反映軌道沉降變形后的性質，應用實例中求解“極狹長”的鈍角三角形面積時并未取絕對值，導致曲率值有正有負。其中正值表示曲線是凹函數，即軌道在該微段下凹；負值則表示曲線是凸函數，即軌道在該微段上凸。下同。由圖可見，軌道的曲率均不超過6.67×10-5m-1，即軌道半徑均不小于15 000 m。由此表明該隧道的曲率滿足安全要求。

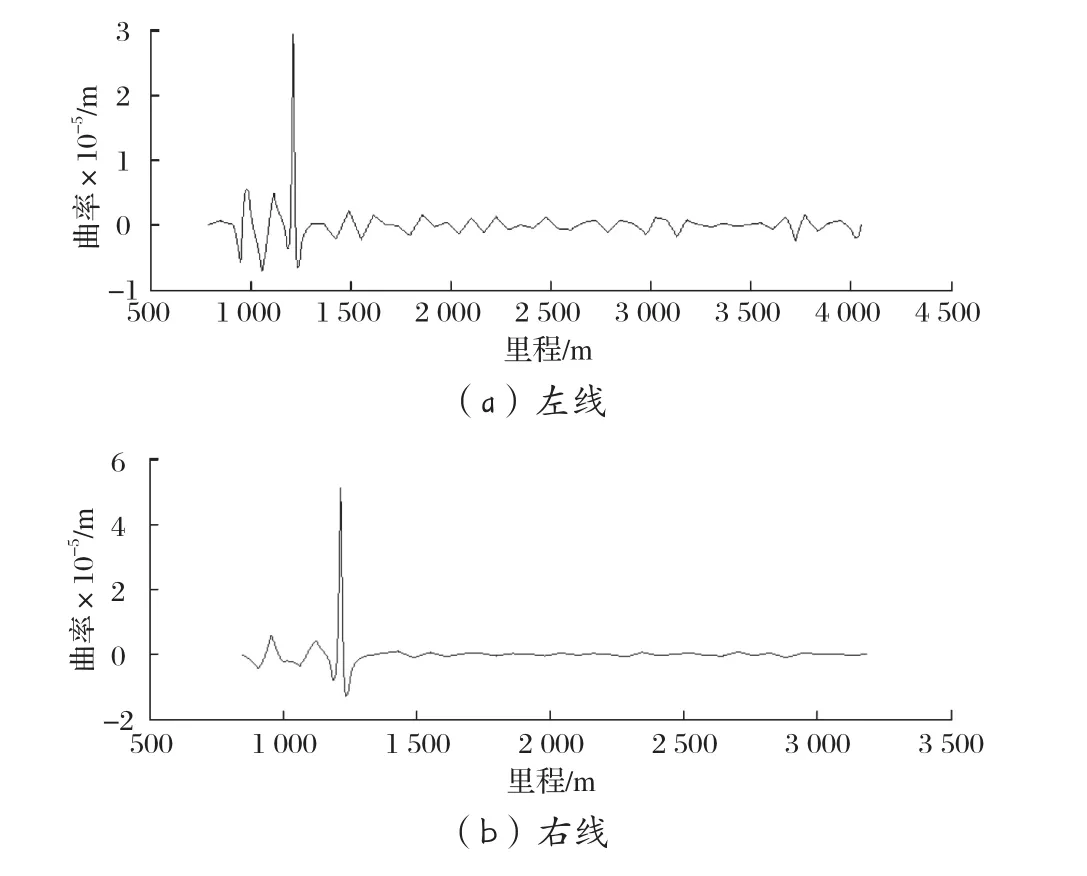
圖5 案例一的軌道曲率

案例二：某地鐵線路的某一區間為盾構段，地勢平坦，地面建筑物眾多，洞身通過段巖性主要為全、強風化花崗巖和硬塑狀花崗巖殘積土，洞頂主要為全風化花崗巖和硬塑狀花崗巖殘積土，未見斷裂，巖土富水性弱。該區間左、右線均約3.6 km，監測點間距均約30 m。其最后一次沉降監測值如圖6中散點所示，根據散點進行三次均勻B樣條擬合得到整個區間的沉降曲線如圖6中實線所示。

采用前文所述的三點定圓法結合坐標頂點行列式求三角形面積方法求解軌道曲率，如圖7所示。同理，軌道的曲率均不超過6.67×10-5m-1，表明該隧道的曲率滿足安全要求。

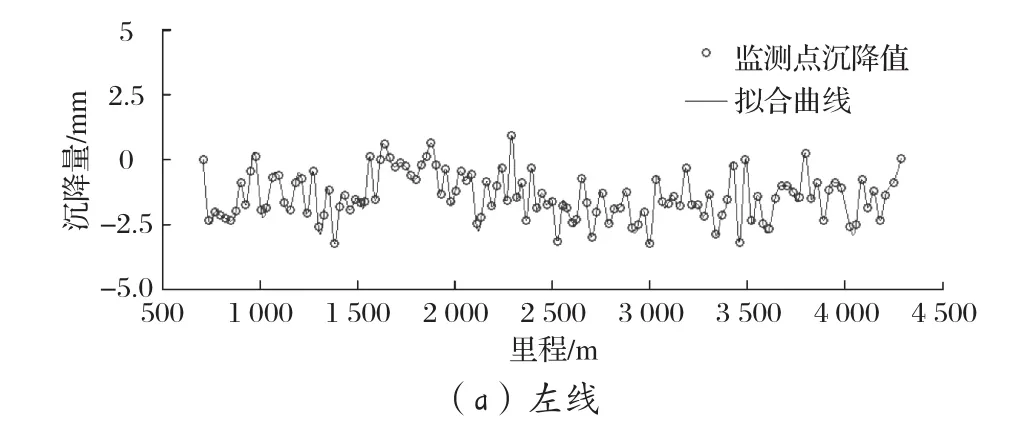
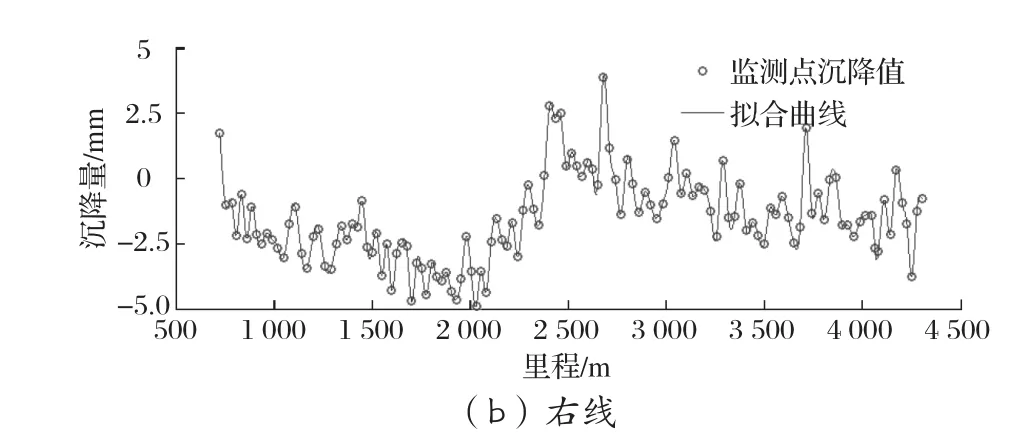
圖6 案例二的監測點沉降值和擬合曲線

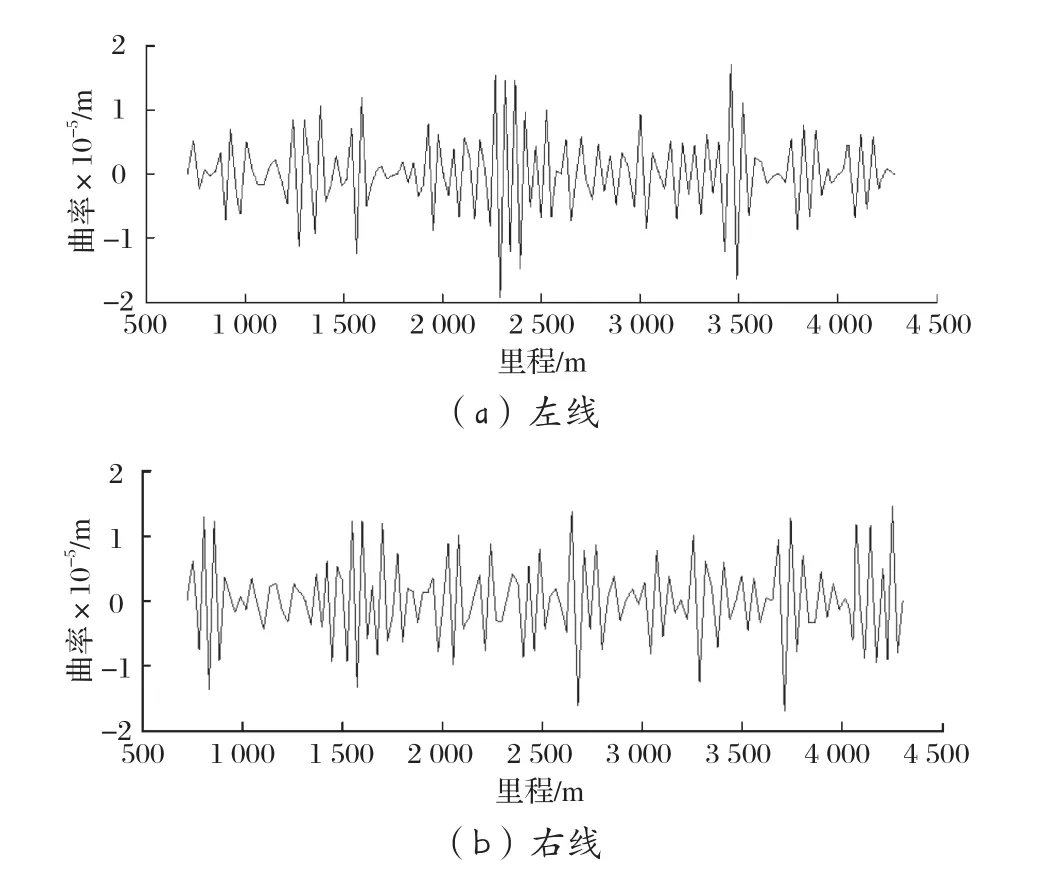
圖7 案例二的軌道曲率

4 結語

文章采用的三次均勻B樣條曲線擬合的方法求得的軌道曲線光滑逼真，能夠真實反映發生沉降后的軌道特點。所述方法在求解軌道曲率方面具有很好的應用空間。