基于偏差映射聚類的目標關聯方法*

劉甲磊，石志廣，張焱

(國防科技大學 ATR重點實驗室，湖南 長沙 410073)

0 引言

近年來，隨著信息技術的發展，適用于復雜場景的多傳感器目標跟蹤方法得到了廣泛的研究和應用[1-3]。它的優勢在于系統通過融合多個傳感器的單獨觀測，可以實現比單傳感器系統更好的跟蹤效果[4-5]。而在多傳感器融合系統中的一個基本問題是目標對象圖(target object mapping，TOM)的匹配，它指多個傳感器同時觀測多個目標時，將屬于同一目標的不同傳感器間的觀測相關聯的過程。簡而言之，就是確定哪些傳感器觀測值來自于同一目標。

一般而言，可以通過傳感器間的空間位置關系，將不同傳感器觀測平面內的觀測值轉換至公共觀測平面內進行處理。理想情況下，這些轉換后的觀測值應該與觀測真值相吻合。但是，在實際跟蹤過程中受應用環境影響，傳感器自身往往存在著系統偏差。不同于傳感器觀測的隨機誤差，系統偏差是一種固定性的偏差，不能通過多次測量消除，計算時它會隨著傳感器間的坐標轉換發生變化。由于偏差和虛假目標的存在，會給關聯問題帶來很多困難，消除這些影響對目標關聯問題具有重要的意義。

在多傳感器數據關聯問題中，一般是對來自不同傳感器系統的觀測集合進行關聯。傳統解決方法的主要步驟是：首先對傳感器系統之間的偏差進行估計；然后，利用估計偏差的統計結果計算形成不同目標分配的代價矩陣；最后將目標間的關聯問題轉化為整體分配代價最小的優化問題進行求解。解決這個問題通常的方法是使用全局最近鄰(global nearest neighbor，GNN)[6]原則，在公共觀測平面內選取最接近的2個觀測值作為同一目標關聯的結果。另外，一些其他的數學方法，如拍賣算法[7-8]和JVC算法[9]等，也成功用于解決這一優化問題。

Blackman[10]提供了許多能有效解決傳感器數據關聯很有意義的方法，但是這些方法通常對傳感器偏差、隨機誤差、虛警和誤檢等十分敏感。Katherine[11]提出拍賣算法解決目標關聯問題，文獻[12]則利用匈牙利算法解決這一優化問題，雖然都能實現比較好的關聯結果，但由于這些優化算法的本質都是選取全局最優解，因此當局部某一目標附近的觀測值關聯代價很接近時，可能會產生錯誤關聯的現象。文獻[13]提出基于目標相對位置的數據關聯方法，但是需已知目標分布隨機誤差來確定分類閾值，并不適用于未知觀測的關聯問題。Roecker[14]提出了一種通過對目標關聯代價矩陣進行合成聚類(agglomerative clustering of biases，ACB)，避開了繁雜的目標關聯代價矩陣的計算及優化求解，從而實現了傳感器目標的快速關聯。但是該方法只利用了目標關聯偏差的距離特性，未考慮多目標空間分布的散布特性，所以對某一目標真值周圍分布了相近目標觀測的復雜情況，依舊不能很好解決。

在本文中，受到文獻[14]對目標偏差距離矩陣進行合成聚類和文獻[15]搜索密度峰值快速聚類方法的啟發，提出了一種基于目標關聯偏差對二維映射聚類來實現目標關聯的方法。該方法將每一種可能的目標關聯偏差對映射為二維平面的一個點，通過搜索點聚類的局部峰值，確定最佳的目標關聯模式。相較傳統方法及文獻[14]中所提方法，它們均局限于對目標關聯代價矩陣的處理，而代價矩陣中只包含目標關聯的距離信息(實質為一維特性)，對于觀測目標的空間散布不具有分辨能力。本文方法可以提取關聯偏差對的方向偏移信息，充分利用了空間中多目標對應到成像平面時分布的拓撲特征，能有效處理較多目標分布接近時的復雜情形，較傳統代價矩陣的方法對目標失配等情形具有更好適應性。

1 問題描述

在本節中給出了一般的傳感器(同一類屬但存在系統型號差異)觀測模型以及不同傳感器間公共像平面的轉換關系。

1.1 傳感器觀測模型

為了方便推導又不失一般性的，有區別地假設2個互相獨立的傳感器系統A和B，其中A為中心傳感器，B為子傳感器。它們同時觀察空間中的N個物體，A檢測到m個目標，B檢測到n目標。每個傳感器系統也可以檢測到實際上不存在于觀測場的虛警引起的一些噪聲雜波，這些雜波會影響關聯結果。傳感器數據關聯的目的是識別共屬于同一原點目標的觀測對，但由于傳感器視場差異、隨機噪聲、誤檢或誤報的影響，會產生目標觀測數目不一致的情形，這會對目標關聯產生很大干擾的，消除這些干擾對目標關聯結果有重要影響。

在這種框架下，傳感器系統可以建模為

(1)

式中：Ai,Bj分別為傳感器A和B的第i和第j個觀測值；Xi,Yj分別為的目標在傳感器A和B成像平面真實位置值；G(P),G(Q)高斯噪聲隨機誤差，均值為0并且對應于傳感器A,B時，其協方差陣分別為P和Q；bA,bB分別為傳感器A和B的偏差矢量。

目標狀態通過狀態向量A和B來描述，并且獨立的傳感器系統中的測量噪聲被描述為具有協方差矩陣P和Q的零均值高斯向量。由于實際上每個傳感器的傳感器偏差變化緩慢，所以在有限的關聯時間內可以被認為是一個常量向量。關聯問題是確定傳感器A和B中匹配的目標觀察對，要求是所有關聯匹配對都是唯一的。換句話說，由A觀察到的每個目標在B中映射0或1個目標。

1.2 公共像平面轉換

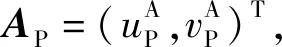
由像平面轉換原理，可知像平面坐標：

(2)

(3)

2 算法描述

(4)

考慮到文獻[15]點聚類算法的優越性，將m×n組可能匹配對的二維偏差映射到偏差平面內，將關聯問題轉化為平面內的點聚類問題。通過合適的搜索原則，找出平面內密度最大的聚類中心，并在一定中心閾值范圍內選取與實際關聯對(可根據實際存在目標數選取，一般為M=min(i,j))數目一致的匹配點，并記錄這些匹配點對應的標簽ID，即可獲得目標圖的匹配信息。

每一個匹配點的局部密度可以寫為

(5)

(6)

選取具有最大局部密度的匹配點為聚類中心，在其四周搜索共M個匹配點。考慮到同一子平臺目標點Xi(xi,yi)與中心平臺目標點Yj(uj,vj)的單一對應關系，建立如下的搜索原則：

(1) 選取具有最大局部點密度max{ρi,i=1,2,…,p×q}的聚類中心點Pcenter，并提取其配對ID{i，j}；

(2) 以該點為中心，依次選取最接近Pcenter的點Pi，檢驗其配對ID，如果不與前面的配對沖突，則將其融合到配對集合A(A={(i→j)|?i∈S1,?j∈S2})中；如果配對ID沖突，即存在i→j1,i→j2或i1→j,i2→j，則選擇更靠近聚類中心Pcenter的組合融合至配對集合中，并跳過該映射點。

(3) 重復(2)，直至選出M組不沖突的最近匹配對為止。

3 BMC算法分析

本節對BMC算法的原理進行實驗分析，實驗場景設置均在三維空間展開，空間內分布傳感器系統A，B以及10個散布目標。設置中心傳感器和子傳感器視場角(FOVA=3°,FOVB=2°)及焦平面參數(FPA：640×640，FPB：512×512)。以中心傳感器A為坐標原點，其位置為[0,0,0],子傳感器B位置為距A水平1 km處[1,0,0]，距A正前方100 km處[0,0,100]，半徑為2 km的球形目標團內隨機分布10個觀測目標。仿真時取傳感器A和B的觀測各為10，分別取傳感器系統偏差(bA=0.5 km，bB=1 km)和隨機誤差(δP=0.1 km，δQ=0.2 km)，并在后續始終保持子傳感器B偏差及誤差特性為中心傳感器A的2倍，以模擬傳感器間各異的系統特性。仿真目標觀測3D分布如圖1a)所示(粗線型標志代表傳感器A觀測位置，細線型標志代表傳感器B觀測位置，同一目標的不同傳感器觀測點共享同一類型標志)，圖1b)為傳感器A和B對目標觀測結果在公共像平面的投影。

觀察來自于同一目標的不同傳感器的觀測值，受傳感器間偏差特性和隨機誤差的影響，其三維空間分布較為散亂(圖1a)示)，不具備直接關聯條件。但將它們投影到公共成像平面時，它們在空間的拓撲特征分布上具有近似的一致性(圖1b)示)。在公共成像平面上，觀察不同傳感器觀測多個對應目標的分布軌跡，可以看出傳感器A的觀測(粗線性標志)在與其標志相同的傳感器B的觀測(細線型標志)對應時，基本都位于其右側，并且從偏差的距離和偏移的方向上，都具有近似一致的特點，很好地反映了目標群觀測之間的相似的拓撲特征。雖然傳感器間空間坐標轉換為非線性關系，但目標間的映射關系不變，由傳感器偏差所產生的確定性特征被很好地保存下來，而相對較小的隨機誤差產生的不確定性特征被掩蓋。這就造成了多目標在不同傳感器成像平面下所成像具有相似的觀測拓撲特征。

利用這一拓撲特征，將每一組關聯匹配對的偏差映射為偏差平面上一點，其分布如圖2所示(紅色星型為坐標原點，圓形散點代表目標關聯偏差對的映射位置，綠色框內為點密度分布最大的區域)，其中具有相似偏差特性的匹配對映射點的位置也幾乎相同，那么局部點密度峰值最大的地方就可以認為是正確的目標關聯匹配模式。圖2可以看到映射點在二維平面內呈現無序的散亂分布，但在綠色框內區域存在點密度分布的極大值，表明這些映射點所對應的目標關聯偏差較其他映射點具有更大的一致性，并且該點集內包含的散點數目基本與目標關聯對數目相同，它們實際上所對應的即是目標關聯對正確匹配的結果。

再分析一種目標失配的情形(圖3a)示)，在公共觀測平面內，此時傳感器A(圓圈表示)有7個觀測值，傳感器B(星型表示)有5個觀測值，并且對于紅色框內的部分，每個傳感器B的觀測附近對應了2個A的觀測值。分別采用本文提出的偏差聚類BMC方法和匈牙利分配法(Hungarian)對其進行仿真，可以看出BMC法對同一目標附近存在多個可能匹配觀測時具有較強的分辨力，它能利用目標的分布偏移信息進行有效的匹配；但通過計算偏差距離矩陣，再進行優化求解的Hungarian法容易受到位置更接近的其他觀測的干擾，產生誤關聯的現象，并且只要干擾觀測的分布在空間上是更近的，那么這種誤關聯現象就不能避免。同理分析可得，以偏差距離為基礎的全局最近鄰匹配(GNN)法和文獻[10]的(ACB)法均不能避免誤關聯情況。

4 仿真結果

在本節中，使用蒙特卡羅方法對算法進行仿真統計分析，并與其他方法性能進行比較。這里比較的方法為：本文提出的基于偏差映射聚類(BMC)的目標關聯匹配法、匈牙利(Hungarian)匹配法、偏差矩陣合成聚類(ACB)法以及隨機選取目標起始的最近鄰法(NN)。每次實驗都將進行1 000次蒙特卡羅仿真。

4.1 仿真場景設置

考慮到實際應用背景，受傳感器系統差異和觀測時的漏檢虛警等影響，極易產生目標失配的情形。假設中心傳感器A可以完全觀察到10個目標，而子傳感器B只能觀測到其中的部分目標，這是更符合實際關聯情況的場景，其他設置不做說明時與3.1節保持不變。

4.2 目標關聯結果分析

首先，考慮一種理想情況。傳感器A和B的視野中都可以完全觀測到這10個目標，此時不存在目標失配的情況，系統偏差沿用3.1節中設定不變，考察這幾種方法隨噪聲誤差變化的匹配性能(圖4)。結果表明，隨目標觀測噪聲增大，其在空間分布趨于散亂，相互之間干擾加劇，給關聯匹配帶來困難，幾種方法關聯正確率均有所下降。并且當δP=1/2δQ≥0.1時，就很難保證有效關聯。但在比較的有效范圍內，本文BMC方法在關聯正確率上略高于Hungarian法，整體性能最優。

圖5為保持目標觀測隨機誤差不變，不同傳感器系統偏差下的算法性能。幾種方法在傳感器偏差變化時關聯正確率比較穩定，表明其對傳感器偏差變化不敏感，其中BMC和Hungarian法較其他2種方法關聯正確率更高，并且BMC法在整體正確率上更優于Hungarian法。

圖6為假設子傳感器B的觀測目標為5個，目標觀測隨機誤差和傳感器的偏差特性均保持不變，中心傳感器A觀測目標數從5～10變化的情況。此時，傳感器B在公共像平面內可能會對應多個傳感器A的觀測，目標的一對一匹配會受到很大的干擾，這也更符合實際應用場景。結果表明，隨中心傳感器A觀測目標數增加，目標關聯失配情形加劇，幾種方法關聯正確率均有所下降。但此時BMC方法關聯性能受影響最小，整體仍能維持在一個較高水平。其他方法對目標失配的干擾更敏感，正確率下降的比較快。這體現了BMC法通過偏差點聚類的方法很好利用了目標空間分布信息，較只分析偏差距離進行關聯匹配的其他方法對干擾目標的甄別能力更強。

表1為3種方法在各種情況下的仿真時間，其中BMC，NN和ACB法在各種情況下的仿真時間基本保持不變，Hungarian算法當目標數增加時，分配矩陣維數增大，匹配時間也隨之增加。BMC法計算時間略長于其余3種方法，但幾種方法計算時間基本在同一量級，相較其較高且穩定的關聯正確率，該算法仍具有很大優勢。

表1 算法仿真時間Table 1 Simulation time of three methods s

5 結束語

本文研究了多傳感器觀測情況下不同傳感器間目標關聯匹配問題，提出了一種基于偏差映射點聚類(BMC)的目標關聯方法。該方法通過計算公共成像平面內的不同傳感器間目標觀測的偏差，并將其映射為二維偏差平面內的點，利用目標空間分布的拓撲特征，通過搜索局部點密度峰值來確定目標匹配的模式并進行關聯。該方法能有效利用了目標空間散布信息，對傳感器間目標關聯保持了很高的關聯正確率，尤其在復雜背景條件下觀測數目不一致產生目標失配時，較其他只利用距離信息的方法更有優越性，能比較有效地克服傳感器間目標虛假觀測的干擾，提高傳感器系統對虛警和漏檢的適應性。