基于STAR-CCM+的潛艇舵翼水動力性能研究

李士強，肖昌潤

(海軍工程大學 艦船與海洋學院，湖北 武漢 430033)

0 引 言

潛艇的操縱性和隱身性是潛艇生命力最主要的2個部分，尾操縱面的結構形式對這兩方面性能有著重要影響。潛艇的尾操縱面大多由舵與穩定翼兩部分構成，一般在設計舵時并不會對艇體以及穩定翼的影響進行充分的評估。近些年來，計算機性能不斷提高、水動力計算軟件功能越來越強大，為小型關鍵附體的水動力研究提供了可能。STAR-CCM+在水動力分析上有很大優勢，其生成的非結構化網格在相同數量上甚至可以與結構化網格相比擬，大大節省了劃分結構化網格所需的時間。SUBOFF潛艇模型試驗數據充足，利用STAR-CCM+對其不同工況下尾操縱面的水動力進行分析，可以更好的認識艇體與穩定翼對舵水動力性能的影響，為優化潛艇舵翼的水動力布局提高潛艇操縱性以及隱身性打下堅實基礎。

1 敞水舵水動力分析

敞水舵的計算分析以及計算方法的準確性驗證是開展系列研究的基礎和前提。

1.1 研究對象

研究對象為實驗數據完備的NACA0018小展弦比翼型，模型為矩形舵，其參數如表1所示。

計算域設置為圓柱形狀，計算域的大小綜合考慮壁面流場干擾和計算量問題，將外域直徑設計為矩形舵弦長的4倍，速度入口到導邊的距離設置為弦長的5倍，對計算影響較大的尾流設置出口到舵隨邊距離為弦長的7倍。

表1 矩形舵模型的主參數Tab. 1 The main parameters of rectangular rudder model

1.2 棱柱層網格研究

第1層棱柱層厚度對壁面y+的影響較大[1]，壁面y+直接影響到計算結果的準確性。為此，對棱柱層網格進行計算分析：

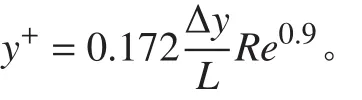
式中： y+為壁面函數無量綱參數； ?y為邊界層最小尺寸， L 為艇長。可以依據公式對 y+進行初步估計，再根據壁面 y+分布情況對棱柱層進行調整。

由于舵相比于艇體較小，同樣來流速度下，舵位置雷諾數不會太高，取Re=1.95x105，base size=0.7 m。棱柱層厚度0.01 m，層數10層。

從計算結果圖1可以看出，當base size=0.7 m控制Prism Layer sketching（PLS）=1.05/1.10時，計算結果與實驗值吻合較好，再減小該值對計算結果的影響不大。相反如果增加增長因子，計算精度、準確性下降，原因在于，此時雷諾數較小，近壁面位置邊界層較厚，當采用壁面函數時，棱柱層的劃分要合理分布在邊界層厚度范圍使得可以較好地模擬流動。此時壁面y+值在30～150之間。

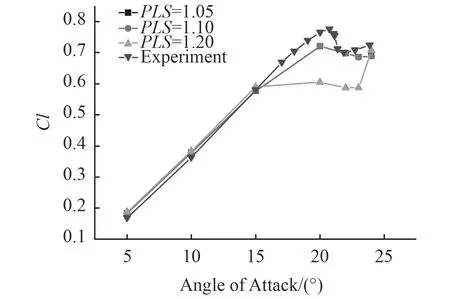
圖1 不同增長因子下升力系數的數值結果與試驗值Fig. 1 Experimental and numerical value of lift coefficients based on different PLS

設置Prism Layer sketching=1.05，對網格離散進行分析。再分別取base size為0.4 m，0.6 m，1.0 m進行研究。計算結果如圖2所示。

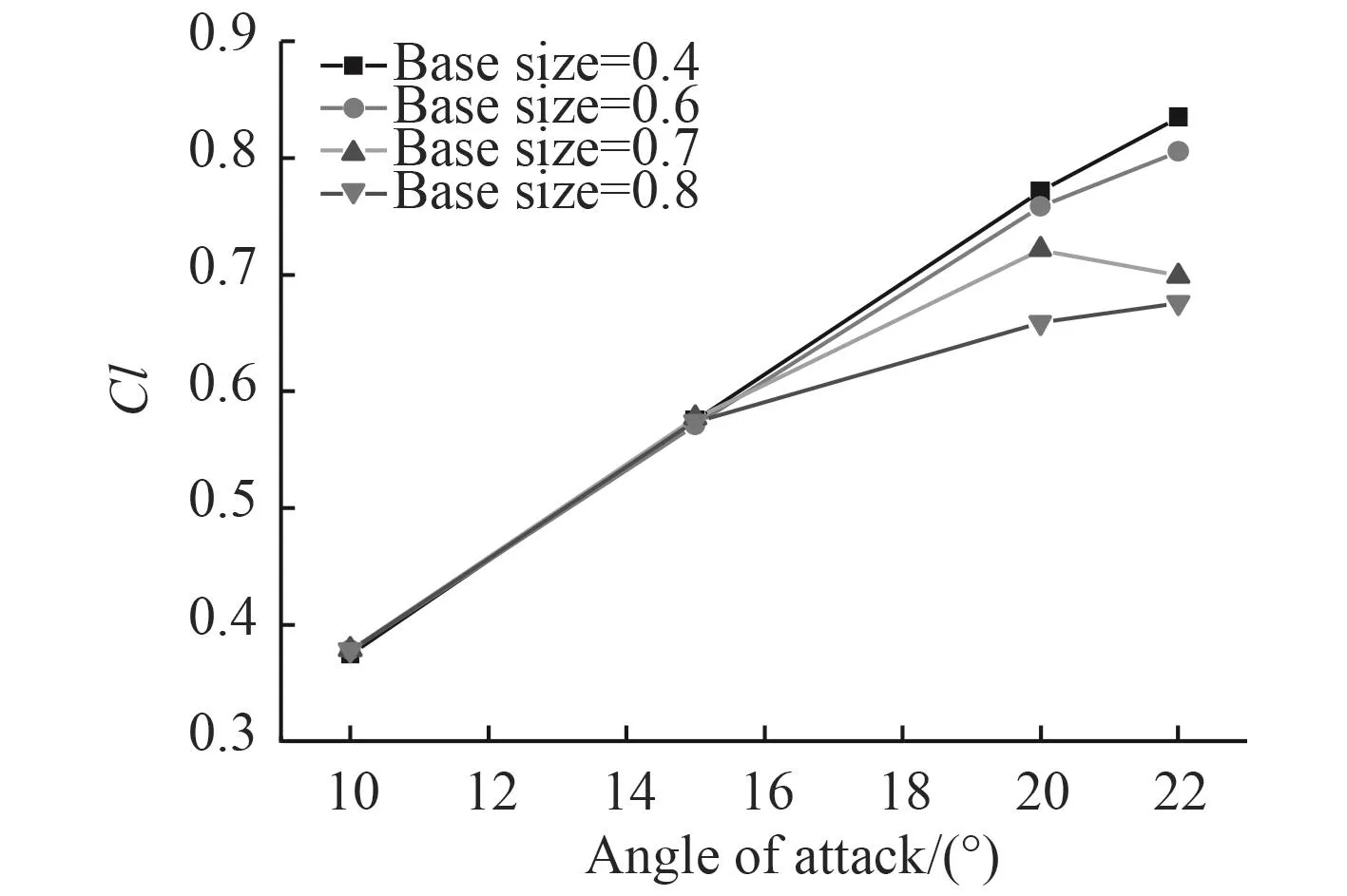
圖2 不同基礎尺寸下升力系數數值Fig. 2 Numerical value of lift coefficients based on different base size

從計算結果可以看出網格數量增多，會使得未失速時的計算更準確；網格數目過小導致整體計算結果的下降，計算也就失去了意義。

1.3 物理模型研究

為了獲得更好的模擬精度以及對運動情況進行研究，有必要研究一下模型與非定常方法。對湍流模型定常計算研究、SST湍流模型利用隱式非定常方法進行計算研究，計算結果如圖3所示。

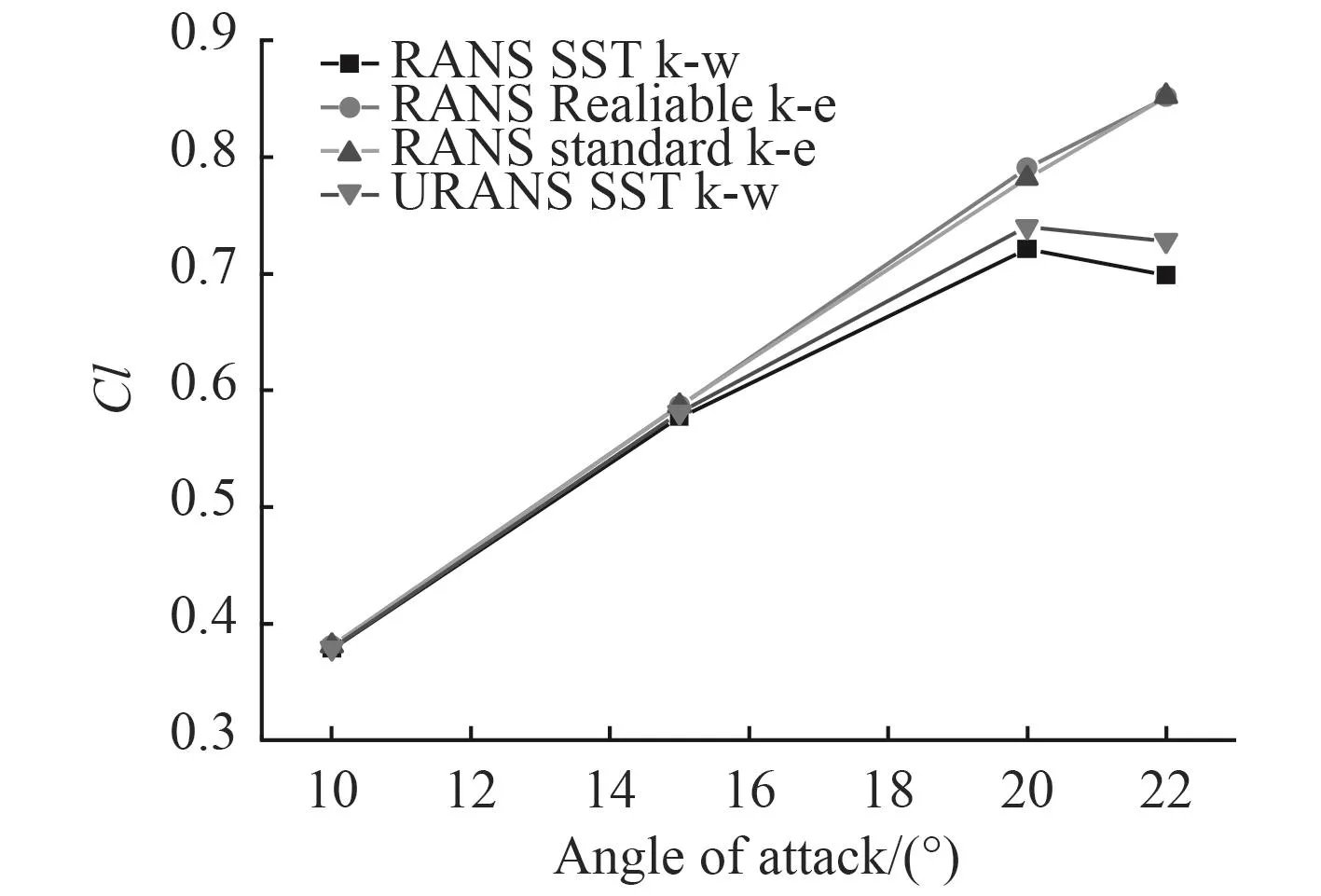
圖3 不同湍流模型下升力系數的數值Fig. 3 Numerical value of lift coefficients based on different turbulence models

對比分析可以看出，非定常方法、定常方法都可以獲得較好的精度，非定常方法計算精度更高。但同樣條件下，在計算未失速舵角的水動力時，模型總體上可以獲得更好一點的精度。由前文對不同湍流模型對阻力的數值模擬研究成果總結，再基于模型模擬未失速舵水動力性能較好這一點，在實際的計算時，可以先通過模型模擬估計得到關心的舵角范圍是否包括失速角，然后未失速時可以仿照本文的參數設計流程對帶附體的潛艇采用模型來進行計算。

2 SUBOFF潛艇上單獨舵的水動力性能分析

2.1 計算模型及網格劃分

計算模型利用SUBOFF Config 1 Fully Appended的水平操縱面。特征長度取為沿艇長方向的最大舵寬0.2 m。可以得知，對舵來說Re=7.51E105。

仿照NACA0018的計算域以及網格劃分形式。該操縱面的網格以及局部棱柱層劃分狀況如圖4～圖5所示。

圖4 舵葉面網格Fig. 4 The rudder blade grid

圖5 舵附近棱柱層網格Fig. 5 Prism layers grid around the rudder

2.2 不同舵角下升阻性能研究

對比分析不同舵角下SUBOFF單獨舵的水動力性能和艇后舵的水動力性能對于認識艇體伴流對舵的影響具有重要意義。控制絕大部分y+都控制在30～150之間。圖6展示了2種物理模型下計算結果的對比。

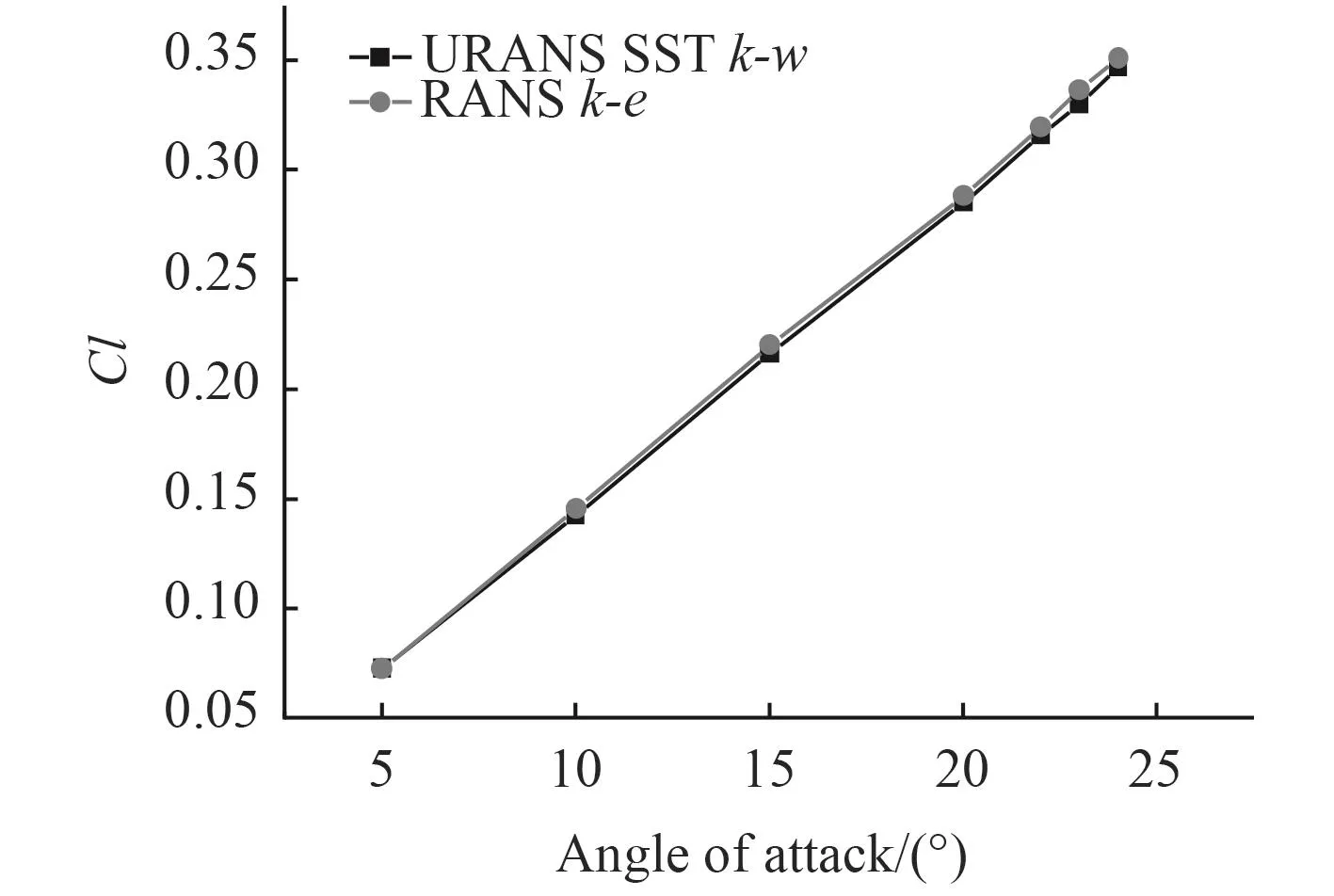
圖6 不同湍流模型下升力系數的數值Fig. 6 Numerical value of lift coefficients based on different turbulence models

試驗表明當雷諾數大于1.2×105時，僅失速角隨著雷諾數增加而增大，未失速范圍的舵升阻力系數不變[3]。相比于NACA0018，除了翼型的差異外，雷諾數增大使得SUBOFF舵失速角后移，在所關心的舵角范圍內，不會出現失速現象。分析計算結果也可以看出，利用非定常模型的計算結果同定常的模型計算結果精度相當。

3 SUBOFF潛艇直航打舵水動力性能分析

3.1 計算模型網格劃分

計算模型利用SUBOFF Config 1 Fully Appended模型。根據流體力學中自由表面水質點的運動理論，可知，自由表面水質點的運動深度方向上衰減的很快，當深度達到1/2興波波長時，可以忽略自由表面興波的影響。當潛艇的航行深度大于1/2艇長時，可以認為不受自由面興波的影響[4]。所以文中以深水中的潛艇為研究對象，可以不計興波。

SUBOFF的實驗研究表明，艇體的無因次水動力系數隨著雷諾數改變而變化，但當雷諾數達到1×107～1.5×107時，可以忽略雷諾數影響和尺度效應。計算時來流速度選為 3.343 9 m/s，Re=1.6×107。

網格劃分考慮因素基本同上，為確保計算的準確性，對小部件、曲率較大的位置采用面控制加密。計算域以及網格劃分結果如圖7和圖8所示。

圖7 計算域幾何Fig. 7 Geometry of computation domain

圖8 艇體表面及域剖面網格Fig. 8 Mesh for submarine and cross-sections of computation domain

3.2 不同舵角下SUBOFF潛艇水動力性計算

對SUBOFF Config 1 Fully Appended模型在初始來流為3.343 9 m/s直航時，在打不同舵角下的航行狀況進行數值模擬。

由表2可知，阻力數值模擬的相對誤差在3.7%以內，可以達到較好的精度。

從速度分布圖9可以看出，考慮艇體伴流的速度分布相比于敞水舵下降很多。利用有拱度的茹可夫斯基升力公式分析可知，舵升力的下降正比于速度的平方；相當平板理論表示摩擦阻力與速度的平方成正比，經驗表明摩擦阻力約與速度的1.83次方成比例。

表2 不同水平舵舵角下阻力系數Tab. 2 Effect of sternplane angle on drag coefficient

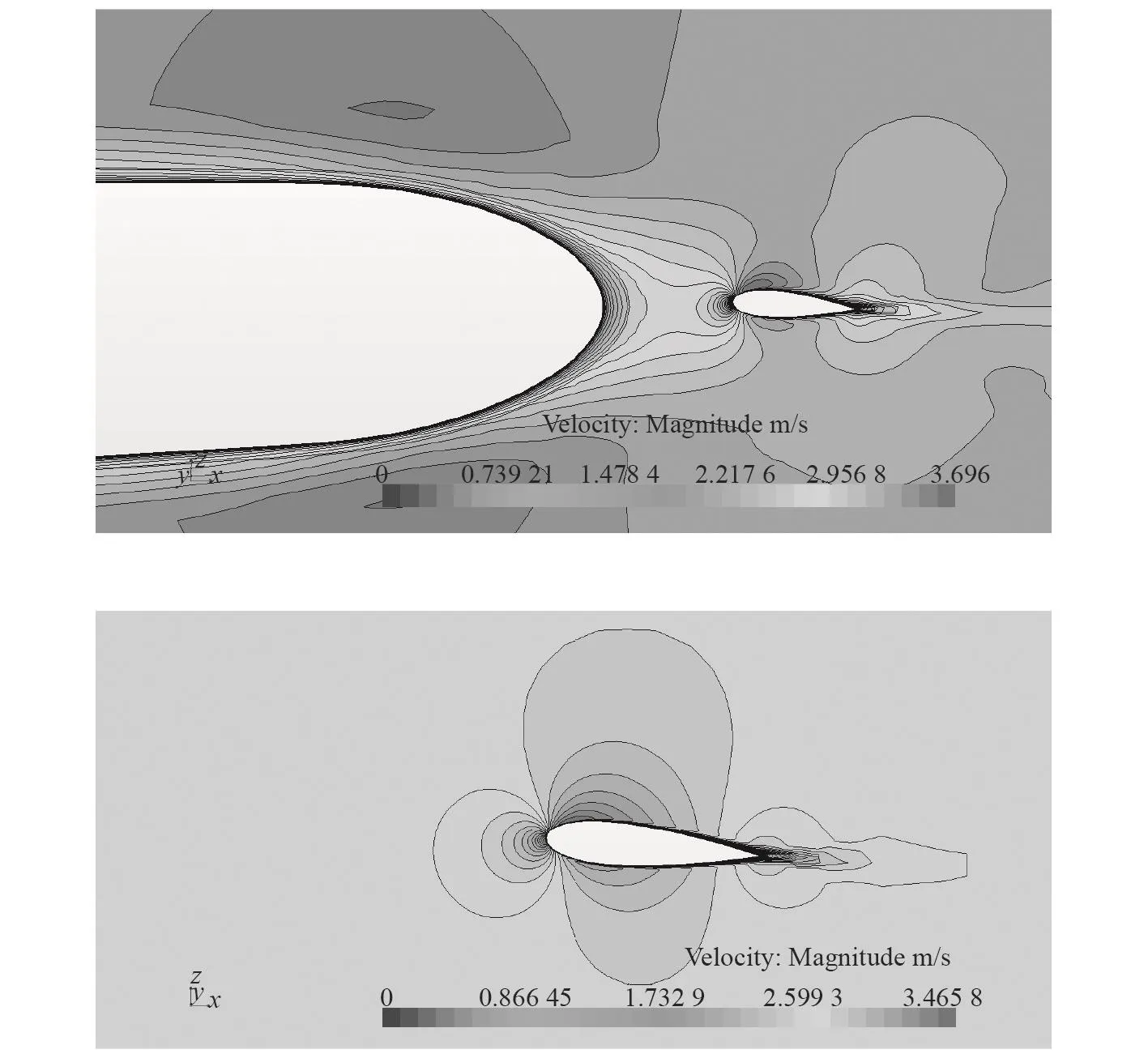
圖9 一縱剖面處速度大小Fig. 9 Velocity magnitude at one longitudinal profile

表3展示了不同舵角下，敞水舵與艇后舵前緣駐點處的最大速度以及用理論、經驗估計的艇后舵相比于敞水舵升阻性能變化百分數。

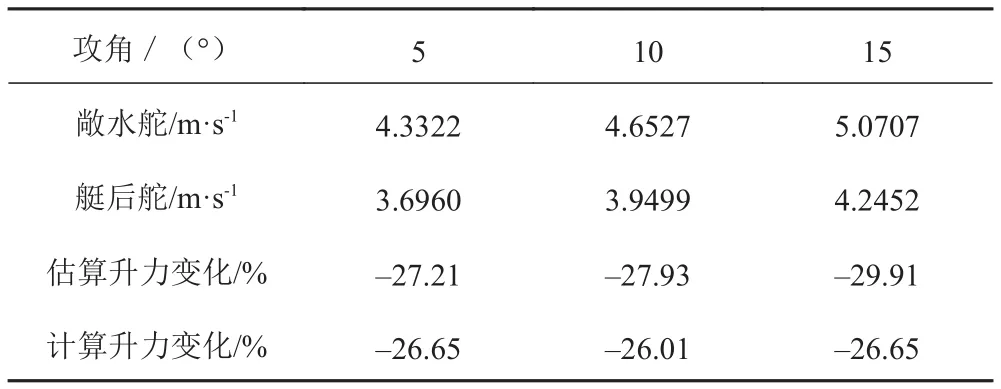
表3 考慮艇體伴流時舵升力變化Tab. 3 Effect of angle of attack on the difference on sternplane considering submarine wake

艇后舵水動力性能的改變是潛艇伴流引起的，艇體的存在使得流場與敞水舵相比變得不再均勻。實際潛艇的舵與穩定翼一起構成潛艇的操縱面，穩定翼的存在就會對舵產生類似艇體流場的影響。圖10～圖13展示了壓力狀況，圖14～圖15展示了渦強分布狀況。

4 SUBOFF潛艇斜航時水動力性能分析

圖10 直航打舵10°迎流面壓力云圖Fig. 10 The pressure cloud picture of one sternplane′s upstream face, 10°sternplane angle

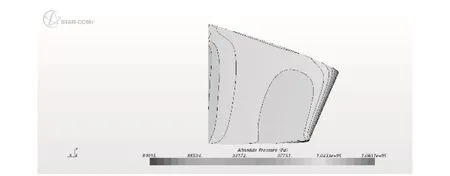
圖11 敞水舵10°迎流面壓力云圖Fig. 11 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle, open-water

圖12 直航打舵10°背流面壓力云圖Fig. 12 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle

圖13 敞水舵10°背流面壓力云圖Fig. 13 The pressure cloud picture of one sternplane′s downstream face, 10°sternplane angle, open-water

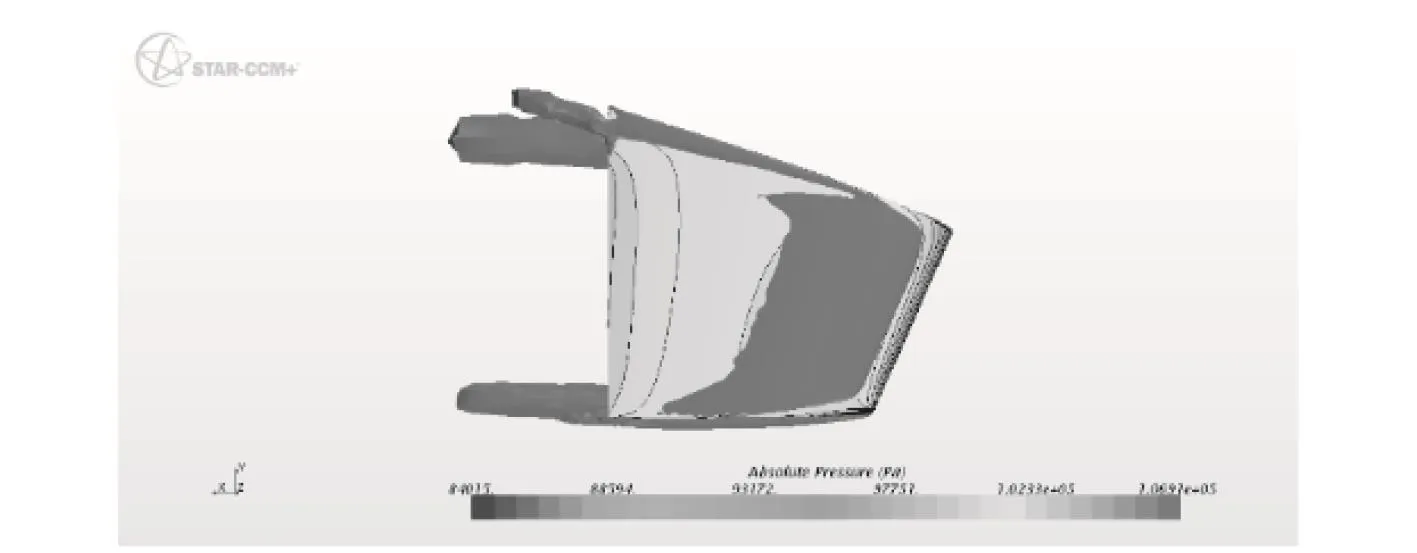
圖14 敞水舵10°迎流面渦強（Q-criterion）Fig. 14 The vortex magnitude of one sternplane′s upstream face, 10°sternplane angle, open-water

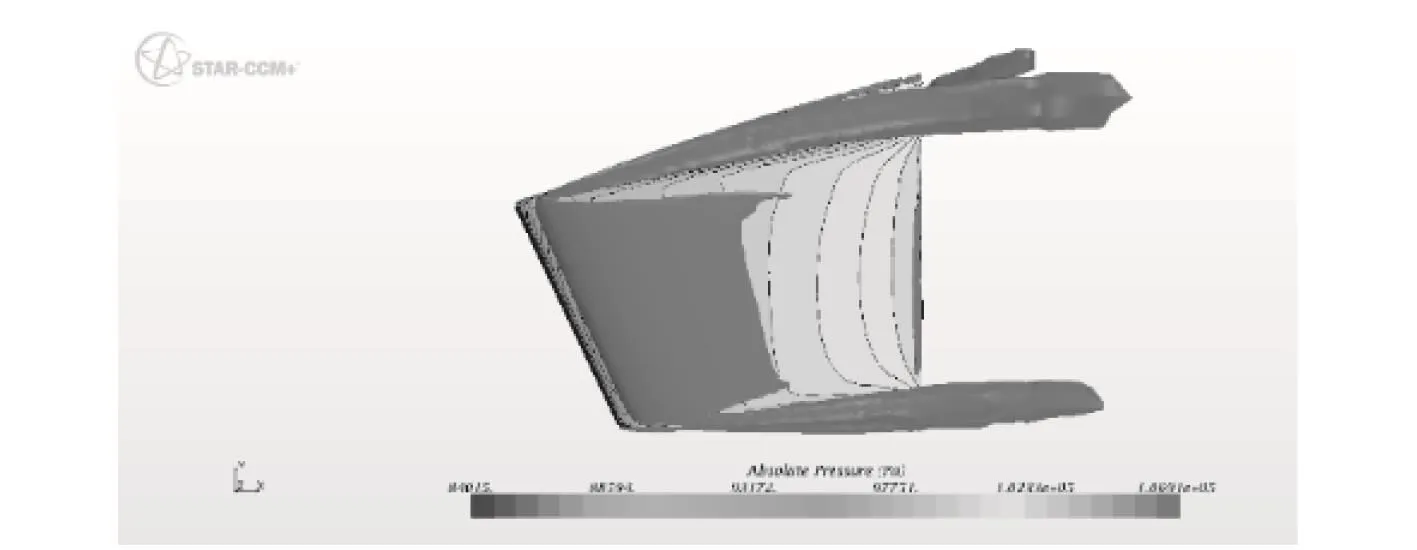
圖15 敞水舵10°背流面渦強（Q-criterion）Fig. 15 The vortex magnitude of one sternplane′s downstream face, 10°sternplane angle, open-water

斜航是潛艇操縱的一種典型工況，對于分析艇體的水動力具有重要意義。基于全附體潛艇模型對潛艇在0°～18°斜航工況進行模擬，斜航沖角間隔2°，采取“攻角掃掠”的方式進行模擬，如圖16和圖17所示。將數值模擬的結果同泰勒水池的實驗值[5]以及風洞試驗[6]的實驗值進行分析比較, 泰勒水池DTRC Uncertainty=20%。同時風洞試驗為了更貼近實尺度時的流動，對潛艇的圍殼上布置了兩排激流絲的狀況也進行了實驗。布置的激流絲，使得附體附近湍流度增加。有無激流絲的風洞試驗效果趨勢一樣，但數值結果有一定差異，如圖18所示。

比較可見，數值模擬的結果同實驗值吻合較好，驗證了數值模擬方法的精度。當沖角較大（12°左右），數值模擬的結果盡管落在實驗區間，但從力矩系數可以看出模擬精度已經開始表現出下滑趨勢。

通過艇體各剖面附近的渦量圖19～圖21可以看出，模擬潛艇斜航，當沖角達到10°時，艇體的背風面就已經出現了流動分離，沖角達到20°時，流動分離已經比較嚴重，出現了渦的脫落，應用RANS方法目前無法捕捉分離渦系的演化過程[7]，模擬失真。

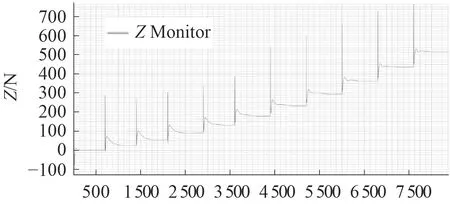
圖16 垂向力Fig. 16 Normal force

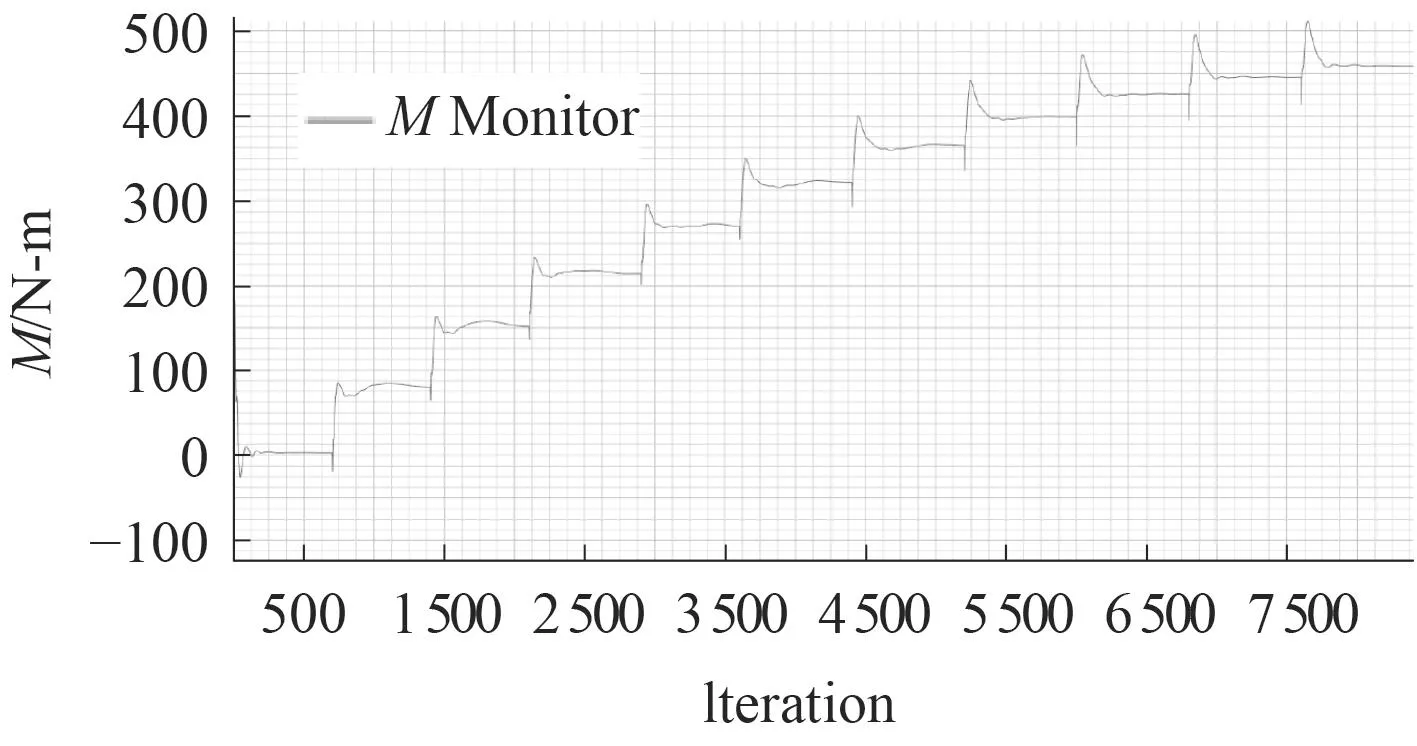
圖17 縱傾力矩Fig. 17 Pitching moment

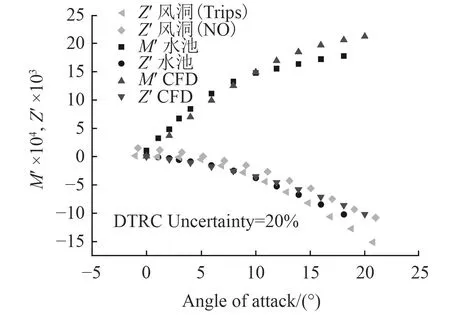
圖18 垂向力和力矩隨攻角變化Fig. 18 Effect of angle of attack on the normal force and pitching moment

潛艇直航打舵與零舵角斜航，在速度入口的速度與舵形成的攻角相同的情況下，舵的水動力卻有很大差異。直航工況下，潛艇附體渦系的變化較為平緩，不會形成大范圍的渦系脫離以致大幅改變舵附近流場的流動。但在斜航工況下，隨著沖角的增大，潛艇背流面渦系發展、脫離速度加快，舵附近的特性相比于敞水以及直航狀況差異明顯。對潛艇舵的水動力系數進行分析，如圖22～圖25所示。

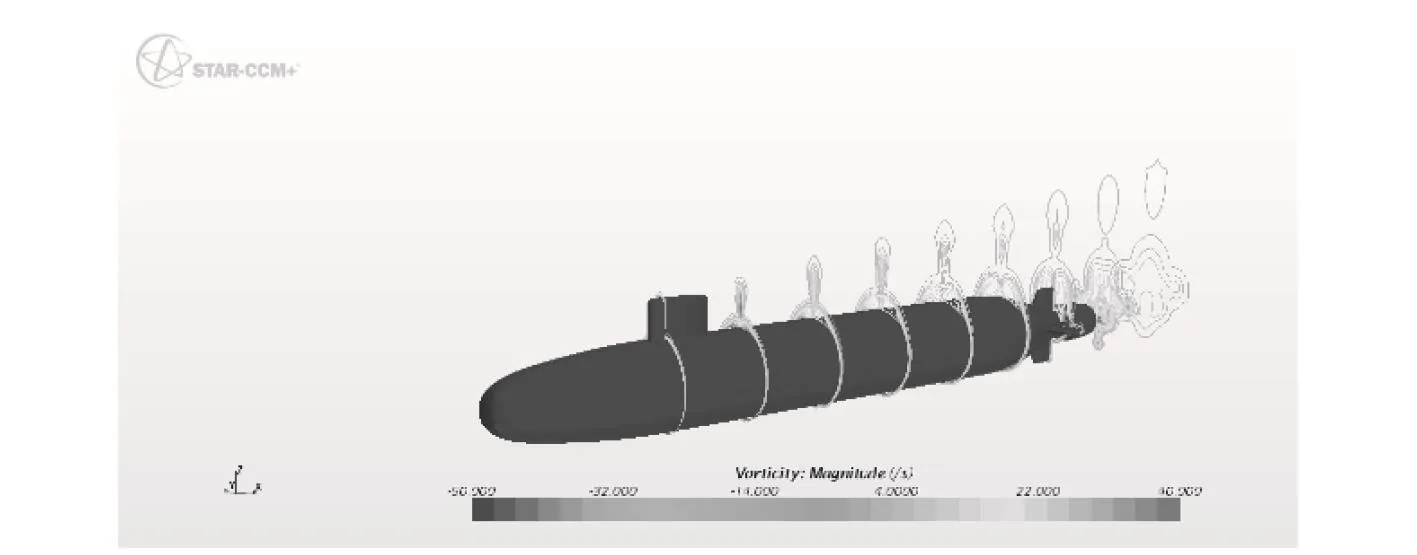
圖19 沖角10°斜航艇體各站渦量分布Fig. 19 Contours of vorticity magnitude at nine axial station,10°angle of attack, pitchup

圖20 舵角10°直航艇體各站渦量分布Fig. 20 Contours of vorticity magnitude at nine axial station,10°sternplane angle

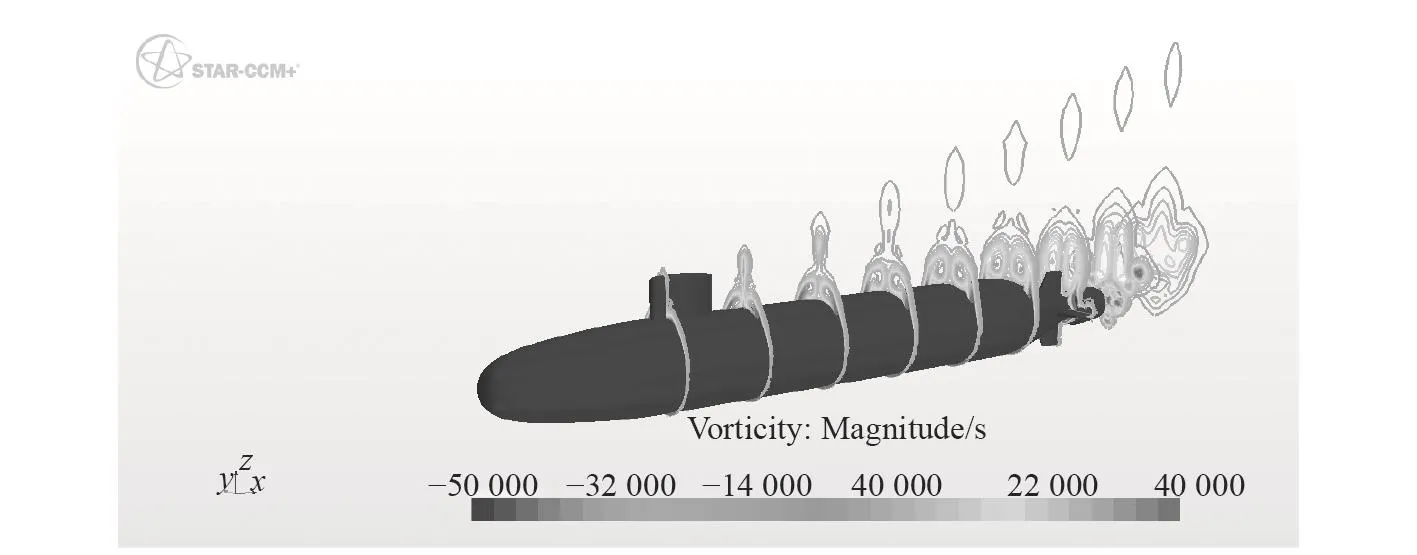
圖21 沖角20°斜航艇體各站渦量分布Fig. 21 Contours of vorticity magnitude at nine axial station,20°angle of attack, pitchup

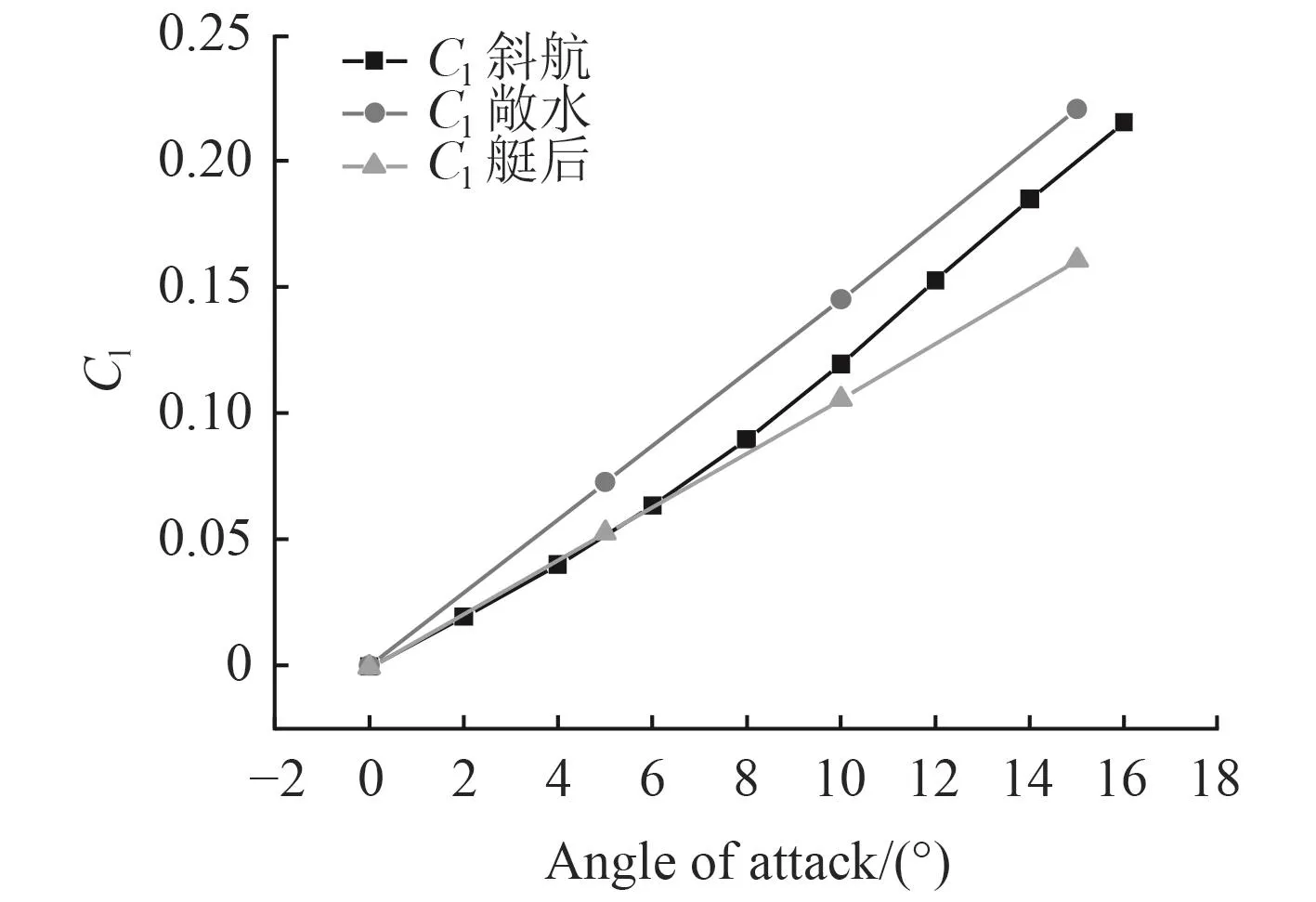
圖22 舵升力系數隨攻角變化Fig. 22 Effect of angle of attack on lift coefficient for one sternplane

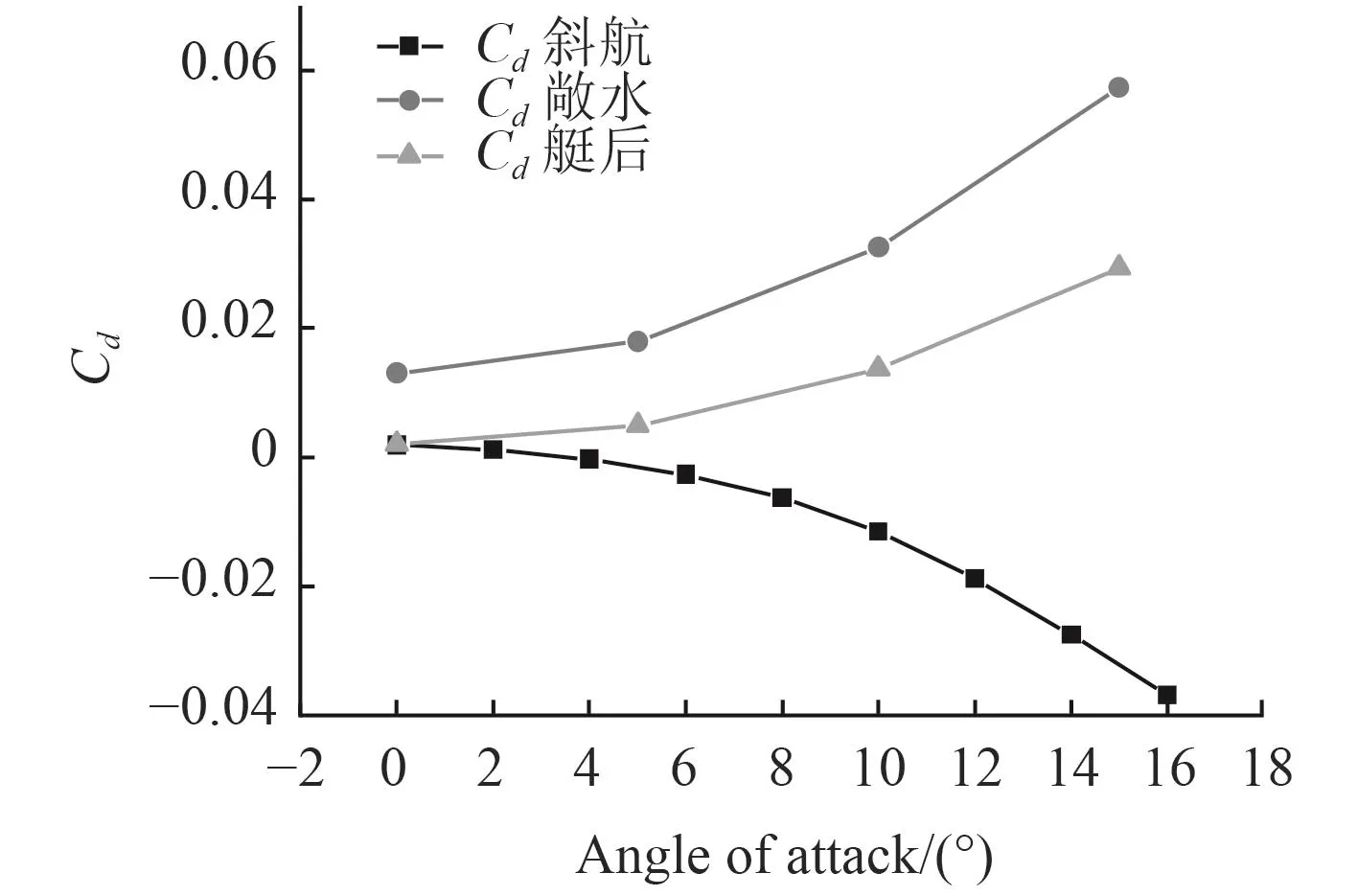
圖23 舵總阻力系數隨攻角變化Fig. 23 Effect of angle of attack on drag coefficient for one sternplane

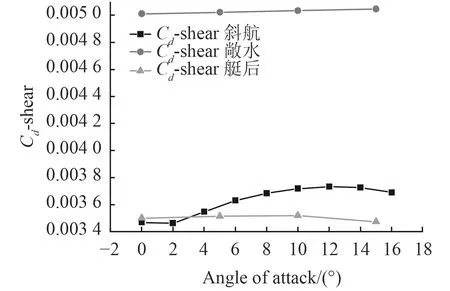
圖24 舵粘壓阻力系數隨攻角變化Fig. 24 Effect of angle of attack on viscous pressure resistance coefficient for one sternplane

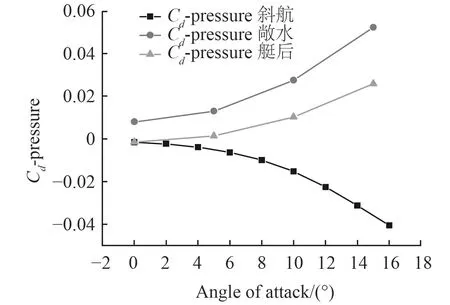
圖25 舵摩擦阻力系數隨攻角變化Fig. 25 Effect of angle of attack on friction resistance coefficient for one sternplane

由于艇體的存在，無論是直航或是斜航，舵的升力系數下降的都較為明顯，這會使得潛艇對操舵的敏感性變差，于潛艇的快速機動性極為不利，降低了潛艇的生命力。特別地，當舵的前端有穩定翼存在時，會造成相似的影響。通過研究可以發現伴流場會對舵的阻力系數產生積極的影響，尤其是粘壓阻力，但舵的面積與整艇相比很小，其阻力只占了較小的一部分。在進行優化設計時，可以視研究所關注的問題，平衡二者之間的關系。

5 結果分析

從數據分析可知，艇體存在時，舵由于受到艇體流場的干擾，實際的水動力效果有所下降。下降的原因直觀上分析是艇體的作用使得舵附近的流場場均勻度下降、舵速度環量變小，這種速度場改變引起的升力以及阻力變化符合理論的定性分析。進一步研究，可以了解流場改變的原因在于潛艇在不同航行狀況下，主艇體以及其附體（如指揮臺圍殼）形成的渦系干擾。通過數值模擬將這種不利影響定性更定量地展現出來，為后續研究工作奠定了基礎。

6 結 語

從簡單翼型舵的敞水性能分析入手，通過研究網格、物理模型對計算結果的影響，確定了物理模型以及網格劃分時應該主要控制的參數。并對全附體的SUBOFF在直航打舵及斜航狀態做了數值模擬，得出以下結論：

1）壁面y+對計算結果的影響較大，應用本文將其絕大部分控制在30～150之間，計算效果較好；

2）對比敞水舵、潛艇直航打舵及斜航時舵的水動力性能，針對關心的艇體干擾問題，得出了由于艇體的干擾舵升力性能下降很大的結論；

3）實際潛艇尾操縱面由舵與穩定翼兩部分構成，穩定翼的存在會對舵的水動力性能產生類似艇體伴流場的影響，通過研究指明了改善艇體、舵和穩定翼結構布局的重要性；

4）通過對渦量的可視化研究，可以發現渦流較強的位置就是舵升力性能變差的位置，要想降低渦激振動以及噪聲，流場的精確控制必不可少，這將催生對傳統潛艇附體結構的改進研究熱潮。