面向時間序列大數據海量并行貝葉斯因子化分析方法

高騰飛 劉勇琰 湯云波 張 壘 陳 丹

(武漢大學計算機學院 武漢 430072)

從地球、經濟到人腦，在瞬態頻率和復雜諧波的演化過程中形成了復雜系統.對于復雜系統的工作機理的探索一直是多學科研究的核心[1].隨著數據采集技術和采集設備的飛速發展，復雜系統研究中對于數據處理的要求越來越高，所需處理數據的規模、維度及復雜性也在迅速增加.海量規模的時間序列大數據記錄了復雜系統在時間和空間尺度上的演化.挖掘時間序列數據的潛在深度信息對于復雜系統過往數據分析和未來行為預測具有非常重要的意義[2].時間序列大數據包含了復雜系統中各個“個體單位”之間以及多個復雜系統間的相互聯系.其外部表征具有數據相關性和多重數據屬性，這一特性也決定了時間序列大數據具有較高的維度.

提取時間序列大數據潛在因子對研究復雜系統的整體機制起著至關重要的作用[3].高維科學數據中的一般潛在低維變量揭示了被觀測系統動力學不斷變化的整體機制.然而數據元素之間復雜的相互依賴關系、數據的高維度和海量的數據規模阻礙了其對整體機制的揭示.在小數據時代，時間序列大數據中低維特征的提取被認為是張量分解的數學問題.然而，直接采用傳統的分析方法——獨立成分分析[4](independent component analysis, ICA)及主成分分析[5-6](principal component analysis, PCA)——無法完整準確地提取出高維張量數據的潛在信息.這些方法使得維度之間的信息丟失和相關性破壞[7]，所提取的線性特征信息物理解釋性較差.平行因子分析(parallel factor analysis， PARAFAC[8])和Tucker模型分解[9]適用于高維張量分解，其中因子化更新通常使用交替最小二乘法(alternating least squares， ALS)[10]或其他相關的替代算法[11-12]來解決.時間序列大數據具有動態增長的數據特征.數據規模不斷增長，小數據時代的張量因子分解方法難以高效地應用于大規模、高維度的時間序列大數據.為保證原始關鍵信息提取的高效和完整，迫切需要開發一種面向大規模高維度的時間序列大數據分解分析方法，以實現快速有效的因子信息提取.

時間序列大數據的數據規模是巨大的，并且在空間中快速增長，無法保證對問題域有足夠穩定的先驗知識，這就導致無法確定張量分解的初始條件.良好的因子化分解初始條件和快速迭代的因子更新過程在大規模高維時間序列大數據分解過程中極其重要的.如何在缺失先驗知識的前提下，適應大規模和超高維的數據特征，快速獲取因子成為了時間序列大數據分析的重要研究挑戰.為了解決上述挑戰：1)基于貝葉斯因子化分解方法，本文提出一種在沒有先驗信息域和無需精確初始化過程即可快速獲取收斂因子的海量并行貝葉斯因子化分析方法(the massively parallel Bayesian factorization approach， G -BF)；2)G -BF通過NVIDIA通用并行計算架構(compute unified device architecture， CUDA)[13]進行核函數映射，并行加速因子化迭代更新過程；3)G -BF使用高維數據映射方法完成對任意維度的時間序列大數據的分解要求；4)此外，G -BF結合粗粒度與細粒度2種并行方式應用于子因子融合框架(hierarchical-parallel factor analysis, H-PARAAC)[14]完成對超大規模張量的因子化分解.

為了評估G -BF的性能，本研究進行了一系列高維張量數據分析實驗并與經過GPU加速的G -HALS算法對比探究G -BF的性能效率.實驗結果表明：1)G -BF在Maxwell架構的GPU運行性能優于G -HALS；2)G -BF在處理高維數據規模、秩和維度等方面具有出色的可擴展性，可處理任意維度數據；3)此外，G -BF應用于現有的H-PARAFAC架構在處理超大規模高維張量時表現了優異的處理速度和性能，打破了可分析數據的規模限制.

本研究方法主要有3個方面優勢：

1) G -BF能夠在無需問題域的先驗知識情況下快速準確地分解大規模時間序列大數據，獲得低維特征因子信息；

2) G -BF針對高維時間序列大數據具有普適性，可分解數據維度可變，不限于3維或其他限定維度；

3) G -BF嵌入到H-PARAFAC架構中作為子張量因子分解過程的解決方案，在分解大規模張量時具有優越的性能，打破了處理數據規模大小的限制.

1 相關工作

針對大規模張量因子化分解問題，許多成功的方法和框架已經得到發展.大型矩陣及張量分解的性能已經成為研究的一大挑戰.針對此問題的相關工作大致從優化分解過程和提高分解性能2個方面入手.

Bae等人[15]提出了一種高效多維并行可視化處理大規模科學數據算法(SMACOF).該算法利用集群消息傳遞接口并行矩陣操作和矩陣劃分，實現了高維矩陣到低維歐氏空間的轉換.

在線性分析問題中，特征值問題、奇異值問題以及QR分解(QR decomposition)問題極其重要.Agullo等人[16]提出了一種將矩陣分解為正交矩陣和上三角矩陣乘積的高效分解方法.該方法利用加速設備節點，采用CPUGPU混合架構來加速QR分解過程.

Tan等人[17]提出了一個矩陣分解庫(cuMF)來優化交替最小二乘法(ALS)方法以求解超大規模矩陣分解.cuMF在單個GPU節點上使用多種策略優化ALS中內存訪問，同時將數據與模型并行化用于最小化GPU通信開銷.

Zou等人[18]提出了一種并行張量分解算法(GPUTENSOR)加速大數據集的張量分解.該方法將大張量分成小塊，利用圖形處理單元(GPU)固有并行性及高存儲帶寬并行相關操作，同時使用零散方式優化計算策略，以避免中間數據爆炸而犧牲性能.

最近，Shin等人[19]提出了用坐標下降法更新參數的大規模高階張量分解算法CDTF.該方法具有良好的數據可擴展性，運行在40個節點(Xeon 2.4 GHz)的Hadoop集群上時，可分解有10億個可觀測條目的5階張量.

本研究的目標是在無需先驗信息情況下高效分解大規模高維張量形式的時間序列大數據.所提出方法的研究包括：1)運行效率；2)分解的維度尺寸；3)可處理大型張量數據規模限制.

2 海量并行貝葉斯因子化分析方法(G -BF)

本節的主要內容包括4個部分：1)介紹貝葉斯分解算法(Bayesian factorization， BF)的理論知識；2)對本文提出的面向時間序列大數據海量并行貝葉斯因子化分析方法(G -BF)的算法設計和并行加速設計的描述；3)簡要介紹G -BF和H-PARAFA框架的融合設計；4)對G -BF為滿足處理任意維度分解需求采用的高維數據映射方法進行闡述.

2.1 貝葉斯分解算法

2.1.1 張量分解概率模型及貝葉斯先驗

定義張量分解的線性模型表達式為

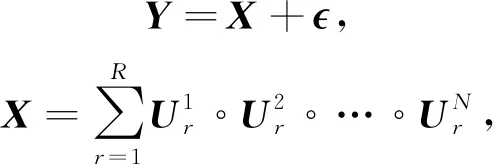
(1)

其中,Y表示大小為I1×I2×…×IN的N維張量，可以由因子張量X和噪聲張量組成，°表示外積，R表示因子矩陣秩，U(n)表示大小為In×R的因子矩陣集合，表示第n個因子矩陣的第r行.

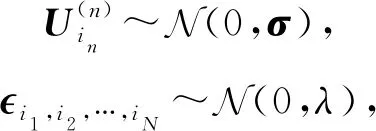
(2)

其中，大小為R×R的矩陣σ和標量λ為超參數.

2.1.2 基于變分貝葉斯推斷的貝葉斯分解

概率模型在變分貝葉斯框架下采用確定性近似推理[20]，將自由能(Free)定義為p(Y)似然估計的邊界下限:

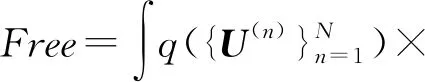
(3)

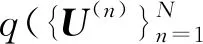
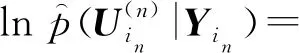
(4)

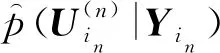
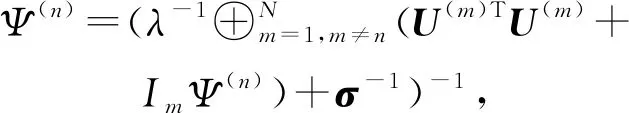
(5)

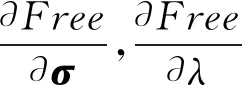
(6)

符號·表示內積.

2.2 海量并行貝葉斯因子化分解方法

2.2.1 G -BF并行加速設計策略

G -BF是基于BF算法理論可以在GPU節點上運行的大規模并行方法.在無需先驗信息及精確因子初始化的情況下，G -BF算法可準確快速迭代地分解大規模張量獲取因子矩陣.本方法涉及的大型矩陣運算操作主要包括Khatri-Rao乘積、Hadamard乘積、逐元除法和矩陣乘法等.利用CUDA進行密集矩陣運算并行加速，實現因子矩陣集的快速更新迭代求解.G -BF將運算過程作為設備并行模塊映射到圖1中CUDA核函數.G -BF分解大規模張量獲取因子矩陣過程根據圖1內容包含8個過程：

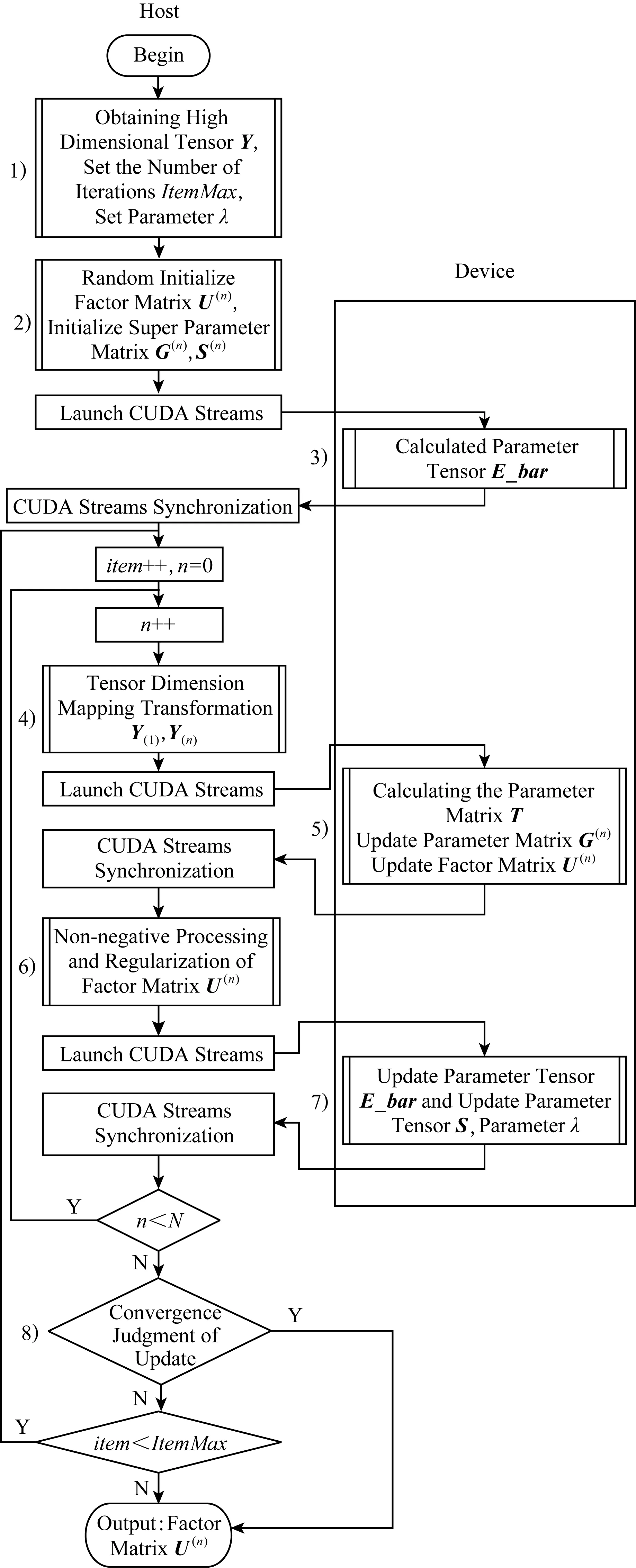
Fig. 1 G -BF method parallel acceleration design strategy diagram圖1 G -BF方法并行加速設計策略圖

1) G -BF的第1步發生在主機端.首先，讀取待處理張量Y，獲取Y的維度大小N、因子化分析過程中表示因子集大小的參數R以及初始化超參數λ.定義G -BF最大迭代次數ItemMax.當迭代次數達到ItemMax時，無論是否達到收斂條件都將停止因子矩陣更新.此參數是限制整個因子化過程的總體耗時的重要參數，當不滿足收斂條件時，ItemMax設定值越大，通過迭代分解獲取的因子矩陣越接近最優解，但耗時也將更大.

2) 該過程初始化G -BF中各項參數矩陣及參數張量，此過程發生在主機端.首先將因子矩陣U(n)隨機初始化大小為In×R的矩陣；S與G是3維張量，大小均為N×R×R,初始化方法為：當第2維和第3維的索引相同時，將值設為0.01，其余元素都設置為0.

3) 該過程在設備端負責計算初始化3維張量，其大小為N×R×R.E_Bar(n)的更新公式為

E_Bar(n)=U(n)TU(n)+InG(n),

這里涉及的運算操作包括矩陣乘法和矩陣加法.根據E_Bar(n)的更新公式可知，各個E_Bar(n)的更新過程相互獨立.上角標n代表更新的不同維度.這里采用并行方式更新，調用cudaStreams執行多個維度的E_Bar(n)的并行更新，每1個cudaStream執行任務相同.第n個cudaStream的執行內容為：將對應第n維的因子矩陣U(n)和參數矩陣G(n)從主機端復制到設備端，主機端調用核函數在設備端計算E_Bar(n)，獲得結果后拷貝回主機端.在完成上述準備后，開始迭代進行因子矩陣U(n)的維度更新，設置item=1，n=1，item表示G -BF實際迭代周期數，n表示G -BF當前更新維度.

4) 高維張量Y的存儲映射.G -BF算法設計要求可分解任意維度張量，但NVIDIA的CUDA計算架構的數據管理固定為1維數據.在G -BF中將張量Y通過張量矩陣化展開方式映射為1維向量進行存儲.當維度更新時，張量元素坐標根據維度間關系設定映射規則轉換.該過程也可以在迭代更新之外完成，如此可減少維度轉換的時間消耗，但這也將增加存儲空間的負擔.詳細的維度映射方法將在2.2.4節給出.

5) G -BF的核心內容，其目的是更新每個迭代循環中各維度的因子矩陣U(n).大致分為3個部分：計算過程參數矩陣T、更新當前維度下參數矩陣G(n)、更新當前維度下因子矩陣U(n).

① 計算過程參數矩陣的主要內容為在主機端初始化過程參數矩陣T，其大小為R×R，數據值全部設為1λ.調用核函數更新設備端過程參數矩陣T，更新公式為T=T⊕U⊕-n,主要涉及的矩陣計算為Hadmard乘積.為減少核函數調用和數據傳輸帶來的時間開銷，將除當前維度之外的因子矩陣合并成1維向量與過程參數矩陣T一同作為Hadmard乘運算核函數的輸入，輸出結果為T的更新結果.

② 更新當前維度下參數矩陣G(n)更新規則為G(n)=(T+S(n)-1)-1，需要通過CUDA進行矩陣求逆和矩陣加法的GPU加速.

③ 更新當前維度下因子矩陣U(n)其更新公式為U(n)={(Y(n)λ)U⊙-n}G(n)，這部分發生在設備端，調用Khatri-Rao乘積核函數直接計算U⊙-n，將N-1個因子矩陣拷貝到1個一維向量作為核函數的輸入參數以便一步直接計算U⊙-n，這樣的方法減少了核函數的調用.(Y(n)λ)U⊙-n由于矩陣乘法特性以及輸入矩陣規模過大導致本過程是整個G -BF中最耗時的步驟.調用設備端矩陣乘法核函數計算得到中間矩陣M，再次調用矩陣乘法核函數計算M×G(n)獲得當前維度更新后的因子矩陣U(n).

6) 對當前更新維度的因子矩陣U(n)進行非負性和正則化處理.通過遍歷將因子矩陣中的負數設為0或某一極小值以及將因子矩陣U(n)以列優先方式進行歸一化.此操作目的是為減少計算復雜性以及滿足H-PARAFAC框架.通過對因子矩陣附加約束，保證了結合H-PARAFAC框架后結果的唯一性.

7) 參數矩陣E_Bar(n)和參數張量S的更新.該更新計算過程在設備端運行.首先更新當前維度中的參數矩陣E_Bar(n)，更新規則為E_Bar(n)=U(n)TU(n)+G(n)，使用CUDA調用主機端的核函數，在設備端進行加速矩陣乘法和矩陣加法運算操作.接下來，更新參數張量S.張量S實際上是1組數量為N且大小為R×R的矩陣集，其中單個矩陣的更新規則為S(n)=E_Bar(n)In+G(n)，任何2個S(n)更新過程彼此獨立，調用N個cudaStreams完成到設備端的并行傳輸并更新矩陣S(n).完成當前維度中的所有更新操作后，n增加1，更新下一個維度.

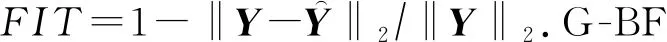
當G -BF中收斂到全局最小值或迭代次數達到預設最大值時，輸出的因子矩陣集為最優因子.

2.2.2 并行加速線程映射策略

G -BF模型中在GPU設備端進行的密集矩陣計算主要包括矩陣的Hadmard乘積、Khatri-Rao乘積、矩陣加減、逐元除法和矩陣乘法.G -BF中的矩陣運算根據線程管理和調用策略的不同分為：

1) 直接映射.輸出矩陣的每個元素直接從輸入矩陣中的單個元素確定.例如，在矩陣Hadmard乘積運算中，通過直接將2個輸入矩陣的第i個元素相乘獲得結果矩陣C的第i個元素，因此設備端線程直接映射到輸入元素.如果輸出矩陣有M個元素，并且核函數總共調用T個線程，那么每個線程最多負責計算(M+T-1)T元素.在G -BF中，Khatri-Rao乘積矩陣、Hadmard乘積矩陣、矩陣加減矩陣和逐元除法都屬于直接映射.算法1以Hadmard乘積為例給出直接映射的代碼設計.

算法1.并行加速——矩陣Hadmard乘積.

輸入：矩陣A大小(AX,AY)、矩陣B大小(AX,AY);

輸出：矩陣C大小(AX,AY).

①row=blockIdx.y×blockDim.y+threadIdx.y；

②col=blockIdx.x×blockDim.x+threadIdx.x；

③offsetX=gridDim.x×blockDim.x；

④offsetY=gridDim.y×blockDim.y；

⑤ fori=coltoAXstepoffsetX

⑥ forj=rowtoAYstepoffsetY

⑦C[i×AY+j]=A[i×AY+j]×

B[i×AY+j];

⑧ end for

⑨ end for

2) 共享內存.輸出矩陣的每個元素由輸入矩陣的1行或1列獲得.矩陣的乘法就是采用這種策略.矩陣乘法的輸出矩陣C的索引(i,j)是輸入矩陣A的第i行和輸入矩陣B的第j列的對應元素乘積的和.若通過直接映射進行矩陣乘法，則每個線程需要將1列和1行元素從全局內存復制到局部內存，這會帶來較高的時間開銷，大大降低計算性能.

本文在G -BF中使用共享內存策略加快矩陣乘法的執行效率.設備端Block中共享存儲器是線程共享的存儲單元，與設備端的全局內存和局部內存相比，具有更高的帶寬和更低的延遲.使用共享內存能夠避免線程將數據從全局內存復制到本地內存的高額時間開銷.在矩陣的乘法中，許多不同的線程使用相同的數據部分，而共享內存可以滿足同一個Block中的線程可以共享數據.因此在對較大矩陣進行乘法運算時可以使用共享內存上的“分塊矩陣”，每個塊物理上對應于設備端的Block.假設2個輸入矩陣A(m×l)和B(l×n)，將每個矩陣劃分成一系列子矩陣(例如Aik和Bkj)，確保對應的子矩陣塊的列等于行.

(7)

2.2.3 G -BF和H-PARAFAC

H-PARFAC框架是以大規模并行方式分解巨大稠密張量的一種解決方案，它使用現代并行和集群計算技術，實現了數據的近實時處理，并且使得提取任意大小和尺寸張量的全部因子成為可能.在大張量分解過程中，H-PARAFAC的分解和融合策略是非常有優勢的.

G -BF在提取大規模高維數據低維信息時，具有優良的迭代效率和性能.該方法能有效分解一個龐大的稠密張量，并且不需要精確的初始化過程即可快速迭代出因子的全局最優解.將G -BF嵌入到H-PARAFAC框架中，它可以完成原來精確初始化模塊中并行直接三線性分解(direct trilinear decomposition，DTLD[6])和子張量分解2個部分的工作，進而加速完成超大規模高維數據的低維因子化分解.圖2展示了G -BF結合H-PARAFAC框架的完整設計.利用分解策略將原始高維張量變換為多個子張量；然后使用G -BF方法，將子張量因子化分解得到子因子矩陣；在子張量經G -BF分解后，利用H-PARAFAC方法將各維度的子因子矩陣進行融合，得到完整的原始張量的因子矩陣；最終完成超大規模高維時間序列張量大數據的分解.

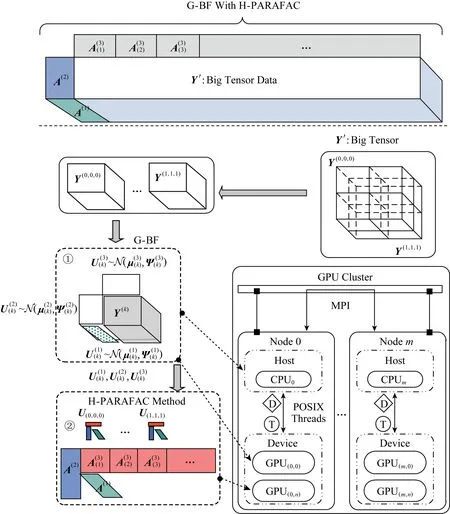
Fig. 2 The design of H-PARAFAC framework with G -BF圖2 G -BF應用H-PARAFAC架構結合設計圖

2.2.4 高維張量的數據存儲映射

由于處理大規模時間序列大數據高維度分解設計目標的限制，張量Y的數據存儲設計尤為重要.在分解過程中，幾乎所有的運算都是矩陣運算和向量運算.在G -BF算法中，將張量Y擴展為矩陣Y(n)進行矩陣運算，其映射策略為：假設N維張量Y中任意元素的坐標為[i1,i2,…,iN]，張量每個維度的大小分別對應為I1,I2,…,IN，則映射到一維向量的元素位置為

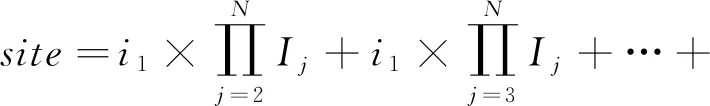
(8)

由式(8)可知，張量中各元素的N維索引與一維矢量Y中的坐標是一一對應的，然后可以直接利用相應的元素進行計算.基于此映射策略來完成4)中提到的張量維度(Y(1)→Y(n))的轉換.在嵌入G -BF的H-PARAFAC框架中子因子融合過程亦采用相似的維度轉換映射規則.

3 實驗結果與分析

本次實驗對本文提出方法的性能進行了評估，并與G -HALS方法進行了對比.實驗包括：1)使用CUDA8.0重新編譯HALS算法G -HALS；2)使用CUDA8.0編譯本文的G -BF算法.所有的實驗都采用了相同的編譯工具g++和nvcc.實驗在1臺裝有NVIDIA GeForce TITAN X顯卡(Maxwell archite-cture)的工作站上進行.具體的實驗環境配置如表1所示:

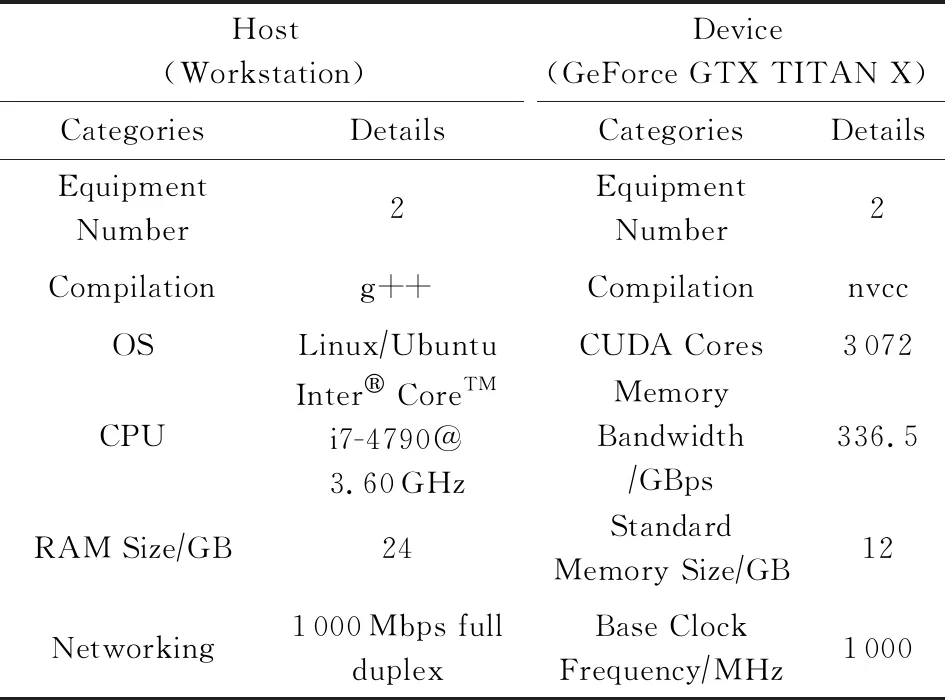
Table 1 Configuration of Experimental Environment表1 實驗環境配置

3.1 運行效率

為了保持性能評估的一般性，本文實驗數據均為由隨機數組成的多通道數據集.在使用G -BF方法進行分析時，采用不同大小的數據集來測試該方法的適用性.隨機生成不同大小的4階張量，張量各個維度大小相同，包括40(404=2560000),50,60,70,80,90,100.

在所有的實驗中，G -BF模型在每個張量上執行20次，每次實驗的迭代次數設置為100次.G -BF模型單次迭代的執行時間如圖3所示，G -HALS和G -BF的單次迭代執行時間隨著數據量增大的變化趨勢大致相同.

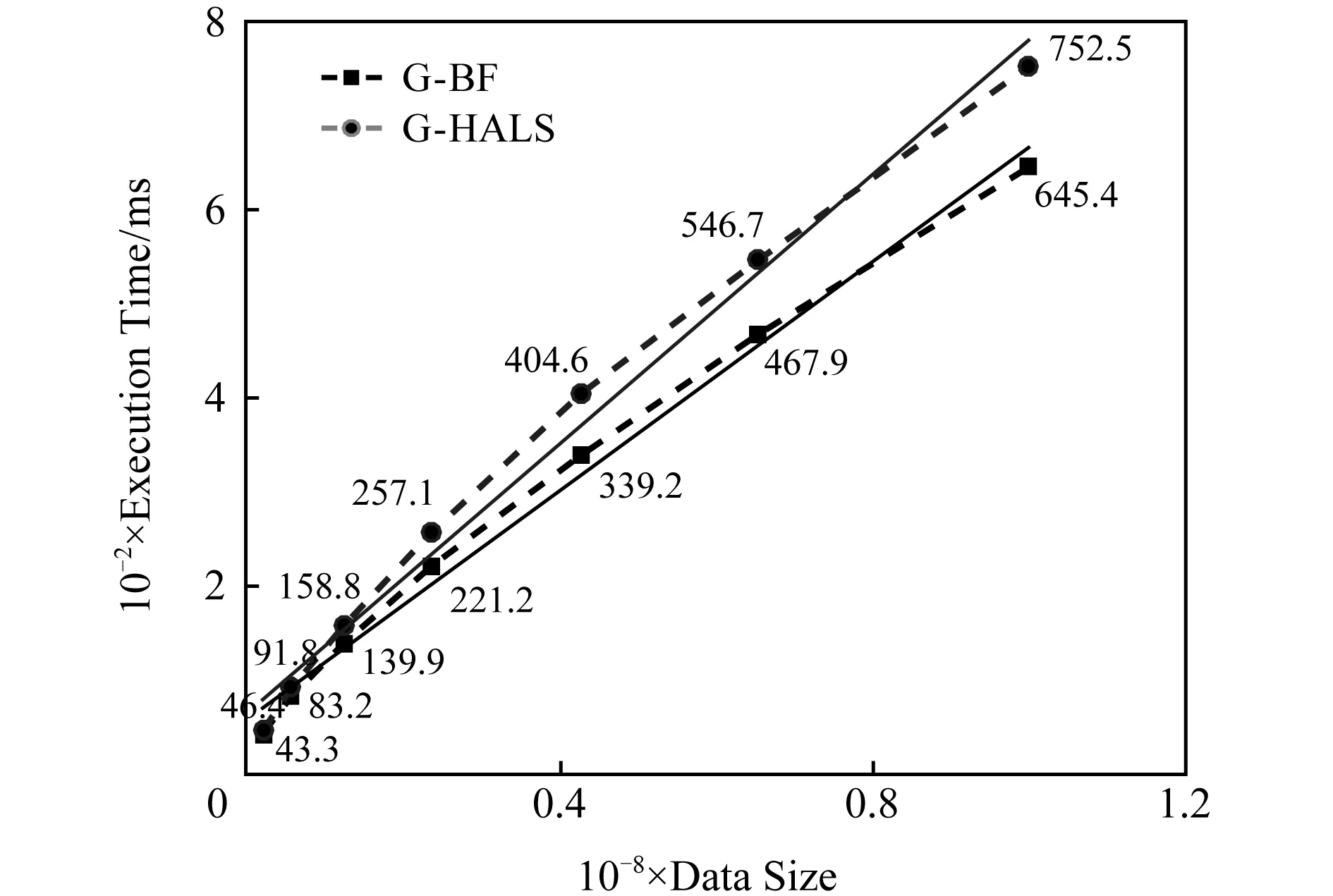
Fig. 3 The single execution time of G -HALS and G -BF processing the same tensor (order-4) with different sizes圖3 G -HALS和G -BF處理大小相同張量單次執行時間(4-階)

G -BF的單次迭代時間范圍為[43.3 ms,645.4 ms]，分別對應于最小體積和最大體積的張量.G -HALS對應的單次迭代時間值為[46.4 ms，752.5 ms].結果表明，G -BF和G -HALS單次迭代的性能都有相同的趨勢.在處理相對小的張量時，由于GPU的基本通信時間和計算能力沒有得到充分利用，G -BF的執行時間接近G -HALS.隨著數據規模的增大，G -BF展現出性能上的優勢，在數據規模非常大的情況下，G -BF在一定程度上能夠減少執行時間.

使用相同的數據大小和截止條件來測試G -HALS和G -BF的迭代終止執行時間.圖4顯示了用G -HALS和G -BF過程分解張量的執行時間隨數據量增長的變化趨勢.在大多數情況下，G -BF的性能優于G -HALS，與上述單次迭代時的趨勢一致.同時與單次迭代時間相比，性能改善更為明顯，主要原因是G -BF在相同的條件下迭代次數較少.圖5顯示了張量分解中迭代次數的變化.相同條件下，在保證分解精度的同時G -BF算法的迭代次數更少，具有減少迭代次數的優點.

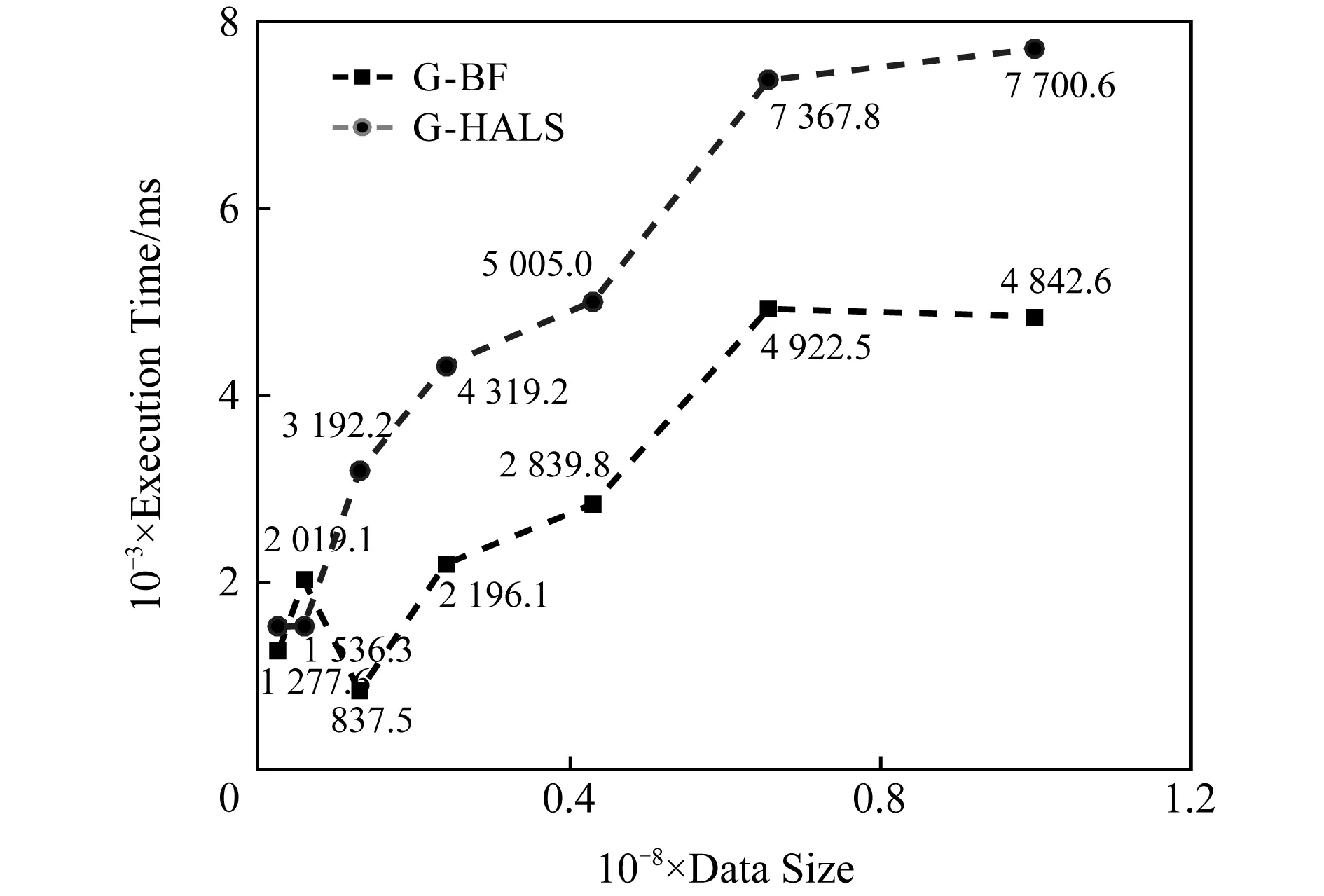
order-4:100×100×100×100 Fig. 4 The breakdown execution time of G -HALS andG -BF factoring analysis of tensor圖4 G -HALS和G -BF處理相同張量迭代終止時間

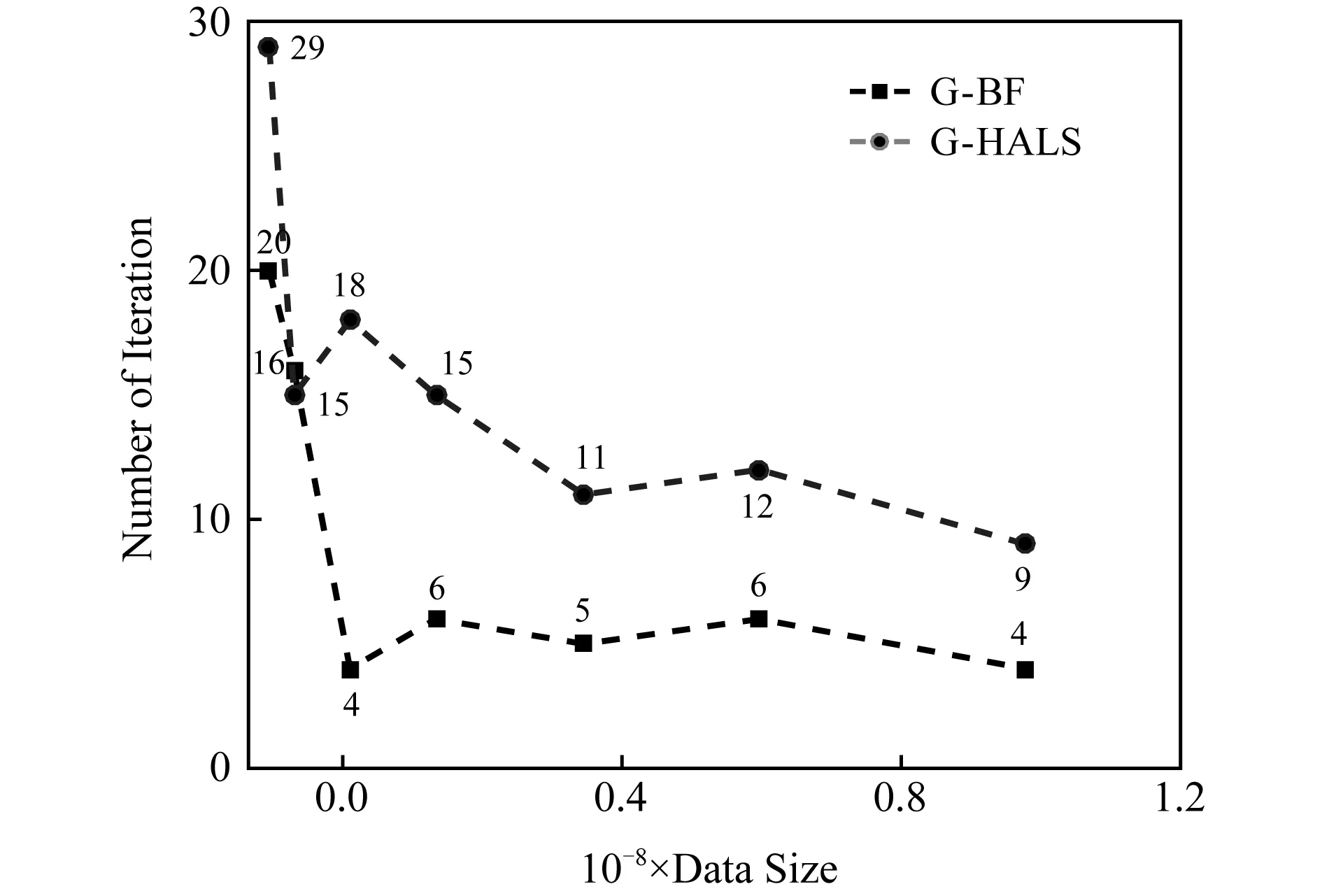
order-4:100×100×100×100 Fig. 5 The breakdown iterations of G -HALS andG -BF factoring analysis of tensor圖5 G -HALS和G -BF分解張量的迭代次數

3.2 可擴展性

圖6顯示了相同數據規模在不同因子數量的分解下單次迭代的執行時間.G -HALS算法的執行時間范圍約為[725.3 ms，771.8 ms]，并且處理時間隨著因子數量的增大而有增加的趨勢.隨著因子數量的增加，G -BF的執行時間[620.5 ms，673.3 ms]具有相同的變化趨勢.以上實驗結果表明：G -BF和G -HALS都具有良好的可擴展性.實驗的數據集大小是固定的(1004=100 000 000)，因子數目作為唯一變量設置為4，8，12，16，20，24，28，32.

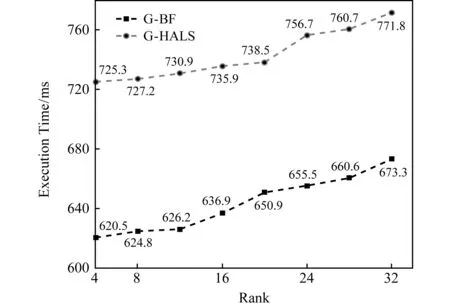
order-4:100×100×100×100 Fig. 6 The single execution time of G -HALS and G -BF processing the same tensor with different ranks圖6 不同秩下G -HALS和G -BF分解張量的單次執行時間

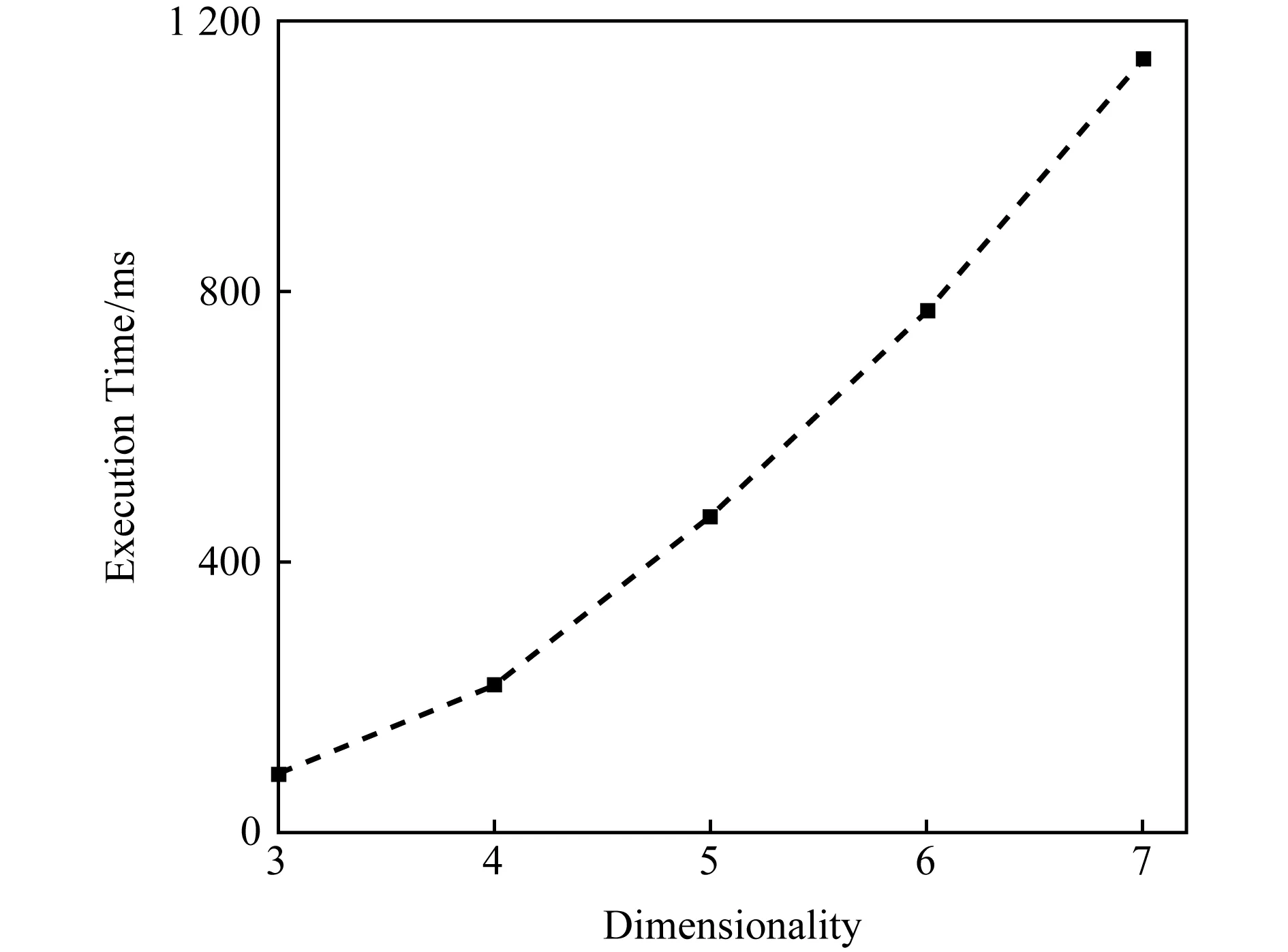
Fig. 7 The single execution time of G -BF processing the same volume (107) of different dimensionality圖7 G -BF處理不同維度張量(107)的單次執行時間

G -BF模型在數據維度上也表現出了良好的可擴展性.圖7顯示了G -BF模型在處理數據規模相同、維度不同時的單次迭代執行時間.隨著張量維數的增加，單次迭代的執行時間也呈上升趨勢.由于算法是基于維度數的迭代更新來求解最優因子，雖然數據量是固定的，但是維度數增長帶來了更多的時間復雜度.實驗表明：該方法適應于處理不同維度的數據，使得任意維張量的分解成為可能.

3.3 處理超大規模張量的性能探究

基于已有工作提出的H-PARAFAC框架[13]，探究G -BF可以處理超大規模的高維張量數據性能.G -BF可同時在多個節點上運行，圖8示出了基于H-PARAFAC在2個計算節點使用G -BF進行張量分解的執行時間.

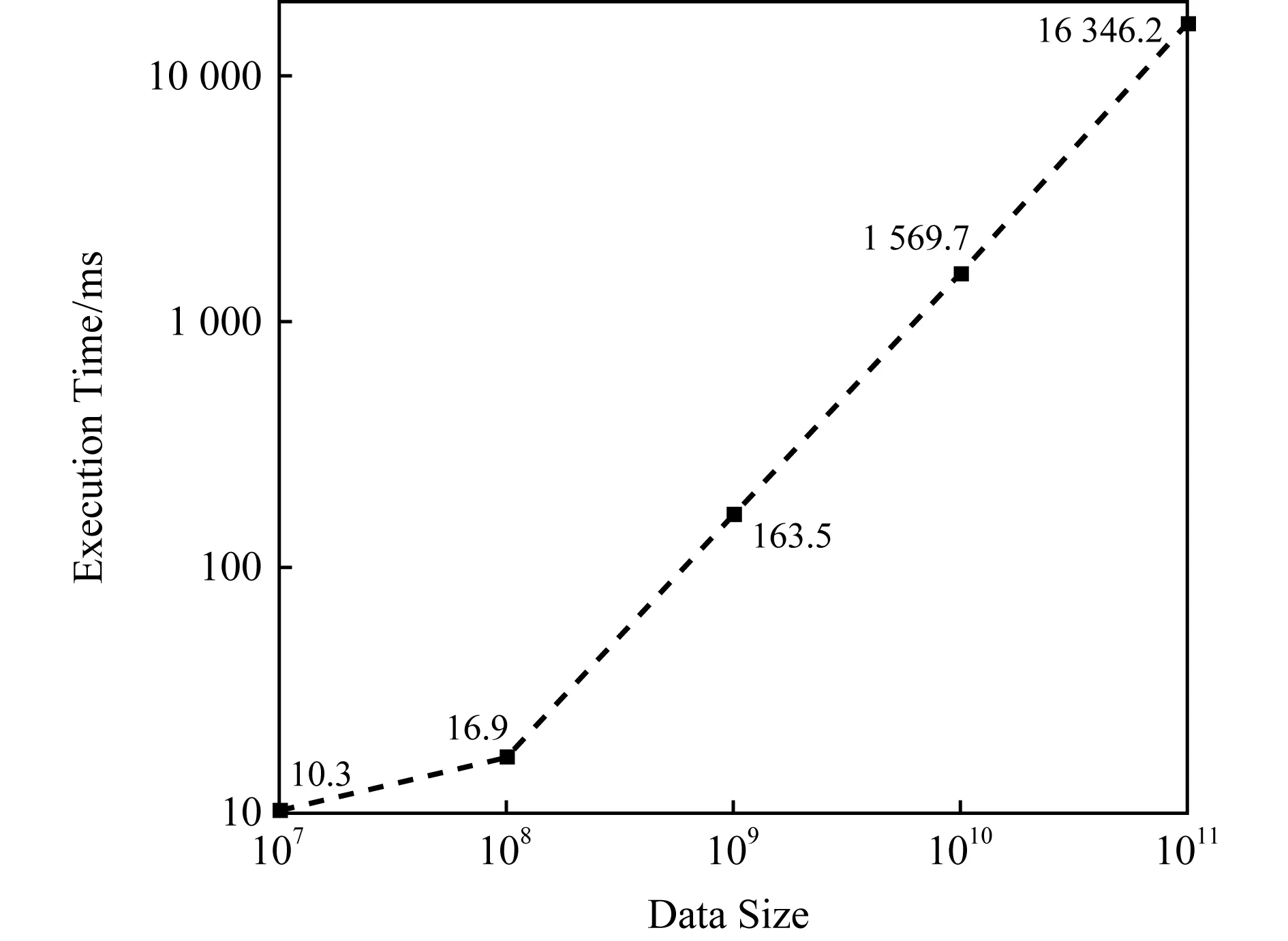
Fig. 8 Total execution time of H-PARAFAC with G -BF deriving sub-factors and full factors of simulated augmenting tensor (order-4) when data scale>108圖8 當數據規模>108時分解大張量總執行時間

圖8上每個值表示處理張量的總時間.其中，數據規模從100×100×100×10增加到100×100×100×100 000,增加了10 000倍;而執行時間從10.3 s增加到16 346.2 s，時間開銷增加了1 587倍.

GigaTensor[21]和CDTF[19]是與這項研究密切相關的2個優秀的張量分解框架.GigaTensor使用100個計算節點可以分解3階稀疏張量(體積=109)，其時間開銷比數據量的增加快得多.CDTF使用運行Hadoop的40個計算節點(Xeon 2.4 GHz)，可以分解具有109個數據元素的5階張量，并且其開銷隨著數據量線性增加.作為對比，G -BF使用H-PARAFAC框架處理109個數據元素大小的4階張量具有更高的效率.當時間大小相同時，結合H-PARAFAC的G -BF能夠處理具有1011個數據元素的4階張量.更重要的是，在處理海量數據時，G -BF打破了數據規模的限制.

4 總 結

先驗知識的缺乏已成為分析高維大規模時間序列的主要挑戰，大多數傳統的因子分解方法不能適應數據的超高維和超大尺度.本文提出了一種海量并行貝葉斯分解方法(G -BF)來分析高維張量形式的時間序列大數據.這種方法具有3個優點：1)在沒有先驗信息的情況下獲得因子矩陣；2)支持可變維度的張量分解；3)在處理大規模數據時保持性能和可擴展性的優勢.

本研究使用GPU來加速密集矩陣的并行運算，高效的存儲器配置方案和高維數據映射策略使得程序能夠滿足任意維度數據的大規模并行需求.同時，更新過程中的中間數據盡可能在設備存儲器中創建和操作，顯著降低了并行編程模型中主機與設備之間的通信消耗.

本文通過實驗探究了G -BF方法在處理不同規模多維張量上的性能，與同一實驗環境下HALS的并行優化算法(G -HALS)實驗作為對比.由實驗結果可得出3個結論：

1) 與G -HALS(常規因子分解算法)相比，G -BF具有更好的性能，并且隨著數據量的增加，其優越性更加明顯；

2) G -BF在數據規模、維度和因子數量等方面具有良好的可擴展性；

3) 將G -BF方法與已有的H-PARAFAC方法相結合，可以對超大張量(2個節點上的體積可達1011)進行因子分解，其性能相比傳統方法顯著提高.

總體而言，G -BF在對大規模多維張量的因子分解方面明顯優于同類算法，針對時間序列大數據的因子降維分析方面具有很大的潛力.