淺談圓的性質在圓錐曲線中的推廣

周仁國，陳 明，溫 藝

（1.遵義師范學院數學學院，貴州遵義563006；2.正安縣第八中學，貴州遵義563400）

1 引言

圓C的半徑為r，點A,B在圓上，滿足條件：由垂徑定理知圓心到直線的距離即弦心距，這一性質（以下簡稱性質）推廣到橢圓、雙曲線、拋物線中，具有相似結論，這些結論是高考的常考內容.

2 性質在橢圓中的推廣

2.1 猜想結論與分析

2.2 性質在橢圓中的推廣

橢圓C上兩點A,B，則原點O到直線AB的距離

（2），由RtAOB面積關系：，將（1）（2）代入有：

設AB所在的直線：y=kx+t與橢圓交于A（x1，y1），B(x2,y2)

3 性質在雙曲線中的推廣

3.1 雙曲線與橢圓的相似性分析

雙曲線與橢圓相似性比較，如下表：

曲線 定義 離心率焦點三角形面積 弦長公式橢圓images/BZ_109_384_1822_401_1838.pngimages/BZ_109_1031_1825_1049_1843.png雙曲images/BZ_109_1030_1918_1047_1936.png線

設想雙曲線C上兩點AB，則的充要條件是：原點O到直線AB的距離

3.2 雙曲線推廣性質的證明

證明與橢圓中的證明相似，要說明的一點是為什么要b＞a，事實上當b≤a時，兩漸近線垂直或所成角為銳角，雙曲線任意兩點（非原點）AB都不滿足

A（tcosa tsina），B（sina tcosa）代入有

4 性質在拋物線中的推廣

4.1 引理

設直線i過點(m,0)，斜率為k，交y2=2px于A（x1，y1），B(x2,y2).聯立

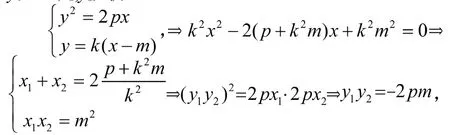
（當m＞ 0，x1、y1異號的；當m＜ 0，x1、y1同號的，當m=0，y1=x1=0）于是得結論

4.2 性質推廣與證明

拋物線與橢圓及雙曲線是有區別的.設A，B是y2=2px上非原點的兩動點，弦心距的最大值dmax=2p.

此性質的另一種表述是：A，B是y2=2px上非原點的兩點直線AB過定點(2p，0).

5 結語

圓是圓錐曲線中的特殊曲線，普通高中數學教材選修4-4(實驗)講到有關圓的伸縮變換問題，實質是圓通過仿射變換成橢圓，因此圓的很多性質是可推廣到橢圓的，這也是比較與類比思想方法的體現，結論的推廣是重要的，多年的高考也經常見到，如2017年的高考20題是關于拋物線問題第二問便是推廣結論的應用，教師在教學過程中和學生在學習的過程認真鉆研這方面的問題，有關圓錐曲線的問題便可迎刃而解了，希望本文對廣大同仁和高考學子有所啟示。