交換交叉立方網(wǎng)絡(luò)在PMC模型下的(t, k)-診斷度研究

郭晨，肖志芳，冷明，彭碩，王博

（1. 井岡山大學(xué)電子與信息工程學(xué)院，江西 吉安 343009；2. 江西省農(nóng)作物生長(zhǎng)物聯(lián)網(wǎng)技術(shù)工程實(shí)驗(yàn)室，江西 吉安 343009）

1 引言

隨著電子工業(yè)的飛速發(fā)展，計(jì)算機(jī)系統(tǒng)中處理器的規(guī)模越來(lái)越大，尺寸越來(lái)越小。而在處理器規(guī)模不斷擴(kuò)大的同時(shí)，計(jì)算機(jī)系統(tǒng)的故障風(fēng)險(xiǎn)也變得越來(lái)越高，由此引發(fā)了一系列可靠性問(wèn)題的研究，其中又以故障的診斷問(wèn)題最為迫切[1]。傳統(tǒng)的故障診斷是通過(guò)一個(gè)所謂的“中心處理器”來(lái)測(cè)試每一個(gè)處理器的運(yùn)行狀態(tài)，從而給出故障評(píng)價(jià)，這種診斷方式工作量巨大并且多數(shù)情況都需要斷電甚至拆解系統(tǒng)，既不精確也缺乏可行性。因此，1967年，Preparata等[2]提出了一種基于圖論的系統(tǒng)級(jí)故障診斷（system level diagnosis）理論。系統(tǒng)級(jí)故障診斷充分利用了每一個(gè)處理器的處理能力，讓處理器之間進(jìn)行相互測(cè)試，通過(guò)綜合分析來(lái)識(shí)別故障。通常情況下系統(tǒng)級(jí)故障診斷可以帶電進(jìn)行。因此，系統(tǒng)級(jí)故障診斷既經(jīng)濟(jì)又便捷，是多處理器并行計(jì)算機(jī)故障診斷的主要發(fā)展方向之一。

系統(tǒng)級(jí)故障診斷的執(zhí)行還依賴特定的診斷策略(diagnostic strategy)。1967年，Preparata等[2]首次將圖論方法運(yùn)用于多處理器并行計(jì)算機(jī)系統(tǒng)的故障診斷，創(chuàng)造性地提出了t-可診斷策略。t-可診斷表示當(dāng)系統(tǒng)的故障處理器數(shù)不超過(guò)t時(shí)，所有故障都可以被診斷出來(lái)。t-可診斷又可以根據(jù)迭代次數(shù)的不同，進(jìn)一步分為一步t-可診斷和順序t-可診斷這2種類型。其中，一步t-可診斷只需要一次迭代即可完成，而順序t-可診斷則需要反復(fù)迭代，直到所有故障都被確認(rèn)為止，每一次迭代都需要有新的故障被確認(rèn)。順序t-可診斷是一種通過(guò)多步診斷來(lái)有效提高系統(tǒng)診斷能力的診斷方式，與一步t-可診斷相比，順序t-可診斷在診斷能力相同的情況下，可以較大程度地節(jié)省測(cè)試成本。

根據(jù)順序t-可診斷的定義可知，在最壞情況下，順序t-可診斷的每一次迭代只能確定一個(gè)故障節(jié)點(diǎn)，因此整體的迭代過(guò)程可能需要很長(zhǎng)的時(shí)間，這大大降低了診斷的實(shí)時(shí)性。基于此，2003年，Araki等[3]提出了新一代的順序t-可診斷理論——(t,k)-可診斷。(t,k)-可診斷要求系統(tǒng)在故障節(jié)點(diǎn)數(shù)不超過(guò)t時(shí)，每次迭代至少可以確定k個(gè)故障節(jié)點(diǎn)。(t,k)-可診斷最壞情況下的最大迭代次數(shù)僅為比順序t-可診斷的最大迭代次數(shù)t要小很多。因此，(t,k)-可診斷改善了順序t-可診斷的過(guò)度時(shí)延，是順序故障診斷的發(fā)展方向。事實(shí)上很多故障診斷理論都存在故障隨機(jī)分布和故障條件分布這 2種情景[4]，(t,k)-可診斷也不例外。在故障隨機(jī)分布的情況下，k=t時(shí)的(t,k)-可診斷就是一步t-可診斷，k=1時(shí)的(t,k)-可診斷就是順序t-可診斷。而對(duì)于故障節(jié)點(diǎn)不是隨機(jī)分布，而是和條件t-可診斷[1]一樣。要求所有的節(jié)點(diǎn)都至少有一個(gè)正確的鄰節(jié)點(diǎn)的情況，2011年，Chang等[4]把這種情況下的(t,k)-可診斷定義為條件(t,k)-可診斷。條件(t,k)-可診斷充分融合了條件t-可診斷和(t,k)-可診斷的優(yōu)點(diǎn)，在有效利用測(cè)試資源的基礎(chǔ)上提高了系統(tǒng)的診斷能力。因此，(t,k)-可診斷和條件(t,k)-可診斷成為了當(dāng)下的研究熱點(diǎn)[5-11]。其中，Chang等[5]通過(guò)研究得出Preparata等[2]提出的PMC模型下超立方網(wǎng)絡(luò)(Qn)、扭立方網(wǎng)絡(luò)(TQn)、交叉立方網(wǎng)絡(luò)(CQn)和莫比烏斯立方網(wǎng)絡(luò)(MQn)的(t,k)診斷度均為。Chen等[6]在此基礎(chǔ)上進(jìn)一步證得MM模型下Qn、TQn、CQn和MQn的(t,k)診斷度為，并進(jìn)一步給出PMC模型下針對(duì)超立方網(wǎng)絡(luò)等分支組合圖(component-composition graph)(t,k)診斷度的通用求法[9]。2016-2017年，文獻(xiàn)[10-11]則分別給出了PMC模型下交換超立方網(wǎng)絡(luò)(EH(s,t))和MM模型下擴(kuò)展立方體網(wǎng)絡(luò)(AQn)的(t,k)診斷度。(t,k)-可診斷改善了順序t-可診斷的過(guò)度時(shí)延，是順序故障診斷的發(fā)展方向。

互連網(wǎng)絡(luò)(interconnection network)是一個(gè)專門(mén)服務(wù)于處理器和內(nèi)存模塊的通信機(jī)制[12]。迄今為止，互連網(wǎng)絡(luò)已發(fā)展成一個(gè)以超立方網(wǎng)絡(luò)及其變種為代表的具有多重繼承關(guān)系的拓?fù)浣Y(jié)構(gòu)集族。交換交叉立方網(wǎng)絡(luò)(ECQ, exchanged crossed cube)[13]是新型互連網(wǎng)絡(luò)的最新研究成果，它同時(shí)集成了交換立方網(wǎng)絡(luò)[14]和交叉立方網(wǎng)絡(luò)[15]的優(yōu)點(diǎn)，是多處理器并行計(jì)算機(jī)系統(tǒng)的一種更加優(yōu)化的組織形式。然而迄今為止，交換交叉立方網(wǎng)絡(luò)中以各種診斷度為代表的可靠性研究，如診斷度、g-正確鄰節(jié)點(diǎn)條件診斷度[16]、(t,k)-診斷度等均未有結(jié)果，這就嚴(yán)重制約了交換交叉立方網(wǎng)絡(luò)的應(yīng)用和推廣。

基于此，本文以交換交叉立方網(wǎng)絡(luò)為研究對(duì)象，首先對(duì)其拓?fù)湫再|(zhì)展開(kāi)研究，在得到交換交叉立方網(wǎng)絡(luò)相關(guān)拓?fù)湫再|(zhì)的基礎(chǔ)上，對(duì)交換交叉立方網(wǎng)絡(luò)在 PMC模型下的(t,k)-診斷度進(jìn)行研究，通過(guò)理論推導(dǎo)得到了交換交叉立方網(wǎng)絡(luò)ECQ(s,t)在PMC模型下滿足(s+1,s+1)-可診斷和可診斷，其中0≤δ＜1，1≤s≤t。進(jìn)而通過(guò)仿真驗(yàn)證了結(jié)論的正確性。本文的研究進(jìn)一步分析了交換交叉立方網(wǎng)絡(luò)的可靠性能，為交換交叉立方網(wǎng)絡(luò)的應(yīng)用和推廣掃清了障礙，具有較強(qiáng)的理論價(jià)值和現(xiàn)實(shí)意義。

2 預(yù)備知識(shí)

2.1 PMC模型

迄今為止，系統(tǒng)級(jí)故障診斷已經(jīng)提出了多種故障診斷模型，但是使用最為廣泛的還是 1967年P(guān)reparata等[2]提出的PMC模型。在PMC模型中，系統(tǒng)用有向圖G(V,E)表示，其中，V表示處理器節(jié)點(diǎn)集合，E表示測(cè)試邊集合。G(V,E)中任意的節(jié)點(diǎn)u表示為u∈V，如果存在著節(jié)點(diǎn)u測(cè)試節(jié)點(diǎn)v，則表示為(u,v)∈E。測(cè)試的結(jié)果用σ(u,v)表示，當(dāng)節(jié)點(diǎn)u對(duì)節(jié)點(diǎn)v的測(cè)試評(píng)價(jià)是正確時(shí)，表示為σ(u,v)=0；否則表示為σ(u,v)= 1。系統(tǒng)所有的測(cè)試結(jié)果統(tǒng)稱為系統(tǒng)的一個(gè)癥候，用σ表示。PMC模型認(rèn)為當(dāng)測(cè)試節(jié)點(diǎn)無(wú)故障時(shí)測(cè)試結(jié)果真實(shí)可信，而當(dāng)測(cè)試節(jié)點(diǎn)本身是故障節(jié)點(diǎn)時(shí)測(cè)試結(jié)果不可信。PMC模型下的測(cè)試規(guī)則如表1所示，其中，u、v表示任意2個(gè)節(jié)點(diǎn)；u=0表示u是正確節(jié)點(diǎn)，u=1表示u是故障節(jié)點(diǎn)；σ(u,v)表示節(jié)點(diǎn)u對(duì)節(jié)點(diǎn)v的測(cè)試結(jié)果。

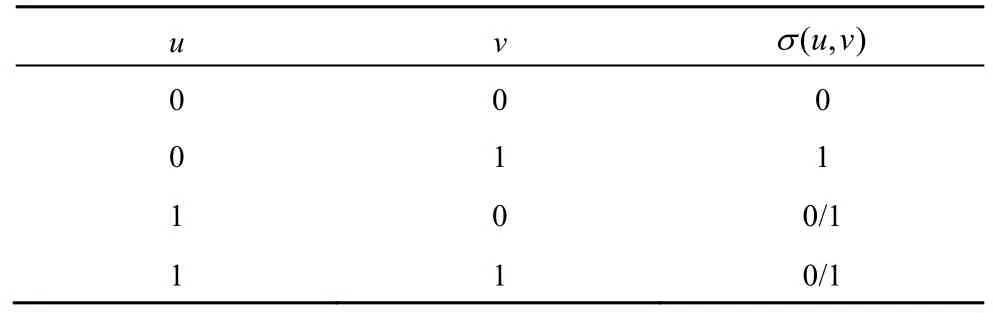
表1 PMC模型的測(cè)試規(guī)則

2.2 交換交叉立方網(wǎng)絡(luò)

交換交叉立方網(wǎng)絡(luò)是 Li等[13]提出的一種新型互連網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)，它同時(shí)繼承了交換超立方網(wǎng)絡(luò)和交叉立方網(wǎng)絡(luò)的拓?fù)湫再|(zhì)，表現(xiàn)出更高的性價(jià)比。

交換交叉立方網(wǎng)絡(luò)的定義需要首先引入關(guān)聯(lián)對(duì)的概念。

定義1[15]設(shè)2個(gè)長(zhǎng)度為2的二進(jìn)制字符串X和Y，其中X=x1x0，Y=y1y0。X～Y表示X和Y是關(guān)聯(lián)對(duì)，當(dāng)且僅當(dāng)(X,Y)∈{(00,00),(10,10),(01,11),(11,01)}時(shí)，X～Y。

定義2[13]交換交叉立方網(wǎng)絡(luò)表示為ECQ(s,t)，其中，s≥1，t≥1。通常用圖G(V,E)進(jìn)行定義，其中，節(jié)點(diǎn)集合i∈[0,s),j∈[0,t)}。V中任意節(jié)點(diǎn)用一個(gè)“s+t+1”位的二進(jìn)制字符串表示，u[i]表示節(jié)點(diǎn)u在位置i的取值用，u[i:j]表示節(jié)點(diǎn)u從第i個(gè)位置到第j個(gè)位置的取值用，其中i≤j。邊集合E包括3種類型，分別表示為E1、E2和E3，其定義如下。

E1：u[0]≠v[0]，且u[(s+t):1]=v[(s+t):1]時(shí)的邊(u,v)∈E1。

E2：u[0]=v[0]=0，且u[t:1]=v[t:1]，存在著正整數(shù)l，(s+t)≥l＞t，有u[(s+t):l]=v[(s+t):l]，如果l-t是偶數(shù)，那么D={1as-2…a0bt-1…b01|ai,bj∈{0,1}forj∈[0,s-2],i∈[0,t-1]}，u[t+2i+2:t+2i+1]～v[t+2i+2:t+2i+1]，其中E2，那么邊(u,v)∈E2；

E3：u[0]=v[0]=1，且u[(s+t):(Δt+1)]=v[(s+t):(t+1)]，存在著一個(gè)正整數(shù)l，t≥l≥1，有u[t:l]=v[t:l]，u[l-1]≠v[l-1]。如果(l-1)是偶數(shù)，那么u[l-2]=v[l-2]。u[(2i+2):(2i+1)]～v[(2i+2):(2i+1)]，其中，那么邊(u,v)∈E。3

由 ECQ(s,t)的定義可知，其中，屬于E1的邊2s+t條，屬于E2的邊2s+t-1t條，屬于E3的邊2s+t-1s條。

ECQ(1,1)、ECQ(1,2)和ECQ(2,2)的拓?fù)浣Y(jié)構(gòu)如圖1～圖3所示，其中虛線、粗實(shí)線和細(xì)實(shí)線分別表示E1、E2和E3。

圖1 ECQ(1,1)拓?fù)浣Y(jié)構(gòu)

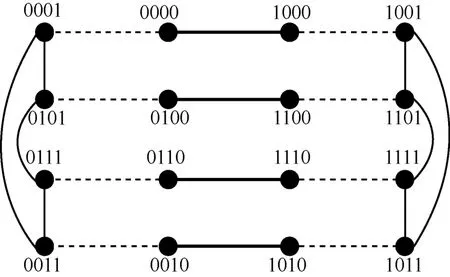
圖2 ECQ(1,2)拓?fù)浣Y(jié)構(gòu)

圖3 ECQ(2,2)拓?fù)浣Y(jié)構(gòu)

ECQ(s,t)具有以下性質(zhì)。

引理1[13]ECQ(s,t)的所有節(jié)點(diǎn)中，c位置取值為0的節(jié)點(diǎn)的度為s+1，c位置取值為1的節(jié)點(diǎn)的度為t+1。

因此可知，1≤s≤t時(shí) ECQ(s,t)的最小度

引理 2[13]ECQ(s,t)可以劃分成 2個(gè)ECQ(s-1,t)或者2個(gè)ECQ(s,t-1)。

由引理 2可以把 ECQ(s,t)劃分為 2個(gè)ECQ(s-1,t)，分別表示為L(zhǎng)和R，其中，L的節(jié)點(diǎn)集，R的節(jié)點(diǎn)集V(R)=。進(jìn)一步把V(L)分為A和B這2個(gè)節(jié)點(diǎn)集合，把V(R)分為C和D這 2個(gè)節(jié)點(diǎn)集合，A、B、C和D的定義如下[13]

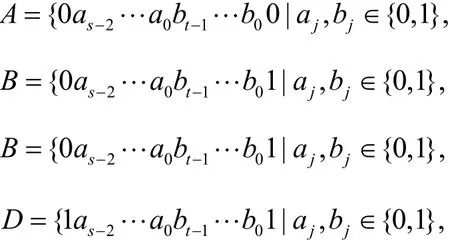
由A、B、C和D的定義可知，2個(gè)端點(diǎn)都屬于A的邊是E2邊，2個(gè)端點(diǎn)都屬于B的邊是E3邊，2個(gè)端點(diǎn)都屬于C的邊是E2邊，2個(gè)端點(diǎn)都屬于D的邊是E3邊，2個(gè)端點(diǎn)分別屬于A和B的邊是E1邊，2個(gè)端點(diǎn)分別屬于A和C的邊是E2邊，2個(gè)端點(diǎn)分別屬于C和D的邊是E1邊。同時(shí)A∪B、A∪C和C∪D都是完美匹配[17]，如圖4所示。

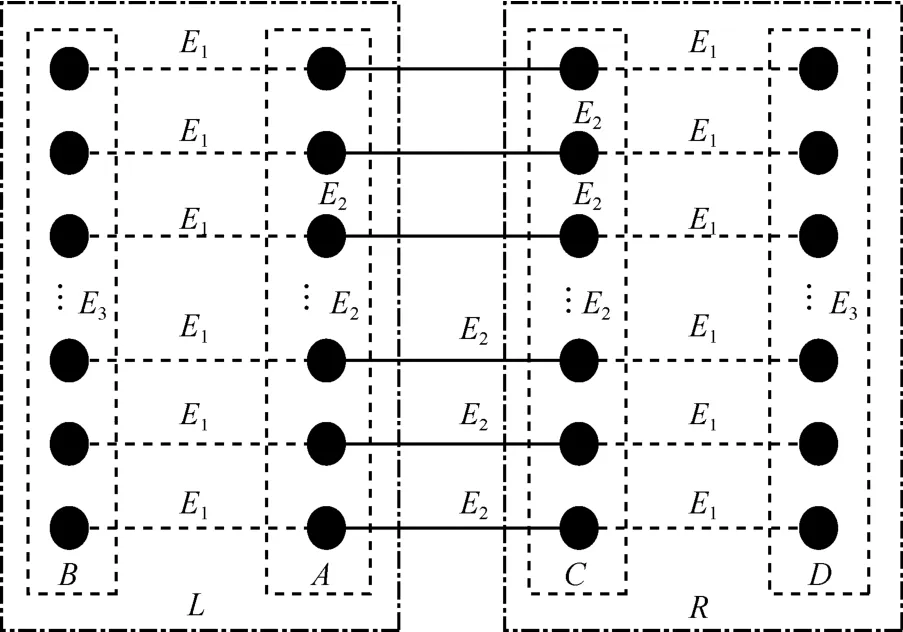
圖4 節(jié)點(diǎn)集合A、B、C、D示意

引理3[13]ECQ(s,t)與ECQ(t,s)同構(gòu)，表示為

引理 4[17]ECQ(s,t)的點(diǎn)連通度k(ECQ(s,t))=s+1，其中1≤s≤t。

引理 5[18]ECQ(s,t)的拓?fù)浣Y(jié)構(gòu)不含節(jié)點(diǎn)三角（triangle-free）。

由引理5可知，對(duì)于ECQ(s,t)中任意的2個(gè)節(jié)點(diǎn)u和v，如果(u,v)∈E(ECQ(s,t))，那么|N(u)∩N(v)|=0，其中，N(u)和N(v)分別表示節(jié)點(diǎn)u和節(jié)點(diǎn)v的鄰節(jié)點(diǎn)集合。

2.3 (t,k)-可診斷

(t,k)-可診斷是2003年Araki和Shibata[3]共同提出的新一代順序t-可診斷，(t,k)-可診斷要求在故障節(jié)點(diǎn)不超過(guò)t個(gè)的情況下，迭代進(jìn)行故障診斷，每一次迭代至少可以識(shí)別出其中的k個(gè)故障節(jié)點(diǎn)，其中k≤t。具體定義如下。

定義3[3]對(duì)于2個(gè)正整數(shù)t和k，k≤t，設(shè)F是系統(tǒng)的故障節(jié)點(diǎn)集合，給定癥候下當(dāng)系統(tǒng)滿足以下2個(gè)條件時(shí)系統(tǒng)是(t,k)-可診斷系統(tǒng)。

1) 當(dāng)|F|≤k時(shí)，所有的故障節(jié)點(diǎn)都可以被診斷出來(lái)。

2) 當(dāng)k＜|F|≤t時(shí)，至少有k個(gè)故障節(jié)點(diǎn)可以被診斷出來(lái)。

給定一個(gè)正整數(shù)k≥1，系統(tǒng)滿足(t,k)-可診斷時(shí)，t可取到的最大正整數(shù)稱為系統(tǒng)的(t,k)-診斷度。當(dāng)系統(tǒng)是(t,k)-可診斷系統(tǒng)時(shí)必然也是(t,k′)-可診斷系統(tǒng)，其中1≤k′＜k。(t,k)-可診斷可通過(guò)引理6進(jìn)行判定。

引理 6[3]系統(tǒng)是(t,k)-可診斷系統(tǒng)，當(dāng)且僅當(dāng)對(duì)于任意故障節(jié)點(diǎn)數(shù)不超過(guò)t的癥候σ，或者其中，是與癥候σ一致的故障節(jié)點(diǎn)集合，并且|F|≤t}。

根據(jù)定義3可知，當(dāng)k=t時(shí)，(t,k)-可診斷就是一步t-可診斷，因此，k=t時(shí)的(t,k)-診斷度可以按照一步t-可診斷的診斷度來(lái)求取，如引理7所示。

引理 7[19]設(shè)系統(tǒng)S有n個(gè)節(jié)點(diǎn)，如果S的點(diǎn)連通度k(S)≥t并且n≥(2t+1)，那么系統(tǒng)S是一步t-可診斷系統(tǒng)。

為了區(qū)分開(kāi)(t,k)-可診斷和交換交叉立方網(wǎng)絡(luò)ECQ(s,t)中的t，下文將把(t,k)-可診斷改寫(xiě)成(t1,k)-可診斷，其定義和性質(zhì)定理維持不變。

2.4 集團(tuán)

集團(tuán)是 1998年張大方等[20]提出了一種特殊的連通分支，集團(tuán)內(nèi)的節(jié)點(diǎn)具有狀態(tài)相同的特點(diǎn)。具體定義如下。

定義 4[20]系統(tǒng)G(V,E)中滿足以下 2個(gè)條件的連通分支H，則稱為集團(tuán)。

1)H中任意相鄰的 2個(gè)節(jié)點(diǎn)之間的測(cè)試結(jié)果都為“0”。

2)H中任意的節(jié)點(diǎn)如果與H以外的節(jié)點(diǎn)相連接，那么它們之間的互測(cè)結(jié)果不能同時(shí)為“0”。

在給定癥候的情況下，可以通過(guò)斷開(kāi)所有測(cè)試結(jié)果為“1”的互測(cè)邊，求取強(qiáng)連通分支的方式來(lái)得出所有的集團(tuán)。以ECQ(1,2)為例，它的癥候如圖5所示，那么斷開(kāi)所有測(cè)試結(jié)果為“1”的互測(cè)邊之后如圖6所示。因此，該系統(tǒng)的集團(tuán)有6個(gè)，分別是{0001,0000,0101}、{0100,1100}、{0111}、{1000,1001, 1101}、{0110,1110,1111}和{0011, 0010, 1010,1011}。

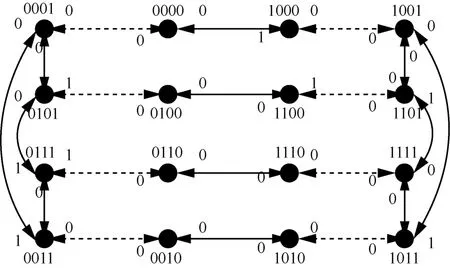
圖5 ECQ(1,2)的給定癥候示意

集團(tuán)具有以下性質(zhì)，如引理8～引理10所示。

引理8[20]集團(tuán)中所有節(jié)點(diǎn)要么全都是故障節(jié)點(diǎn)，要么全都是正確節(jié)點(diǎn)。

圖6 圖5中包含的集團(tuán)示意

通常情況下把全部是正確節(jié)點(diǎn)的集團(tuán)稱為正確集團(tuán)，把全部是故障節(jié)點(diǎn)的集團(tuán)稱為故障集團(tuán)。

引理9[21]如果系統(tǒng)的故障節(jié)點(diǎn)數(shù)不超過(guò)t，那么系統(tǒng)中節(jié)點(diǎn)數(shù)大于t的集團(tuán)必定是正確集團(tuán)。

引理10[21]正確集團(tuán)只能和故障集團(tuán)相鄰。

G(V,E)在給定癥候下的所有集團(tuán)歸為集合V+，不同集團(tuán)之間的鄰接集合E+，表示為E+={(X,Y)|X∈V+,Y∈V+,(x,y)∈E,x∈X,y∈Y}。由此可以把G(V,E)表示為G+(V+,E+)。集團(tuán)集合V+的獨(dú)立子集V+′，指的是V+′?V+并且V+′中的任意集團(tuán)之間都不相鄰。

定義5[5]?(x1)表示m可取到的最小正整數(shù)。指的是在G+(V+,E+)中，V+存在著一個(gè)滿足的子集V+′，是V+的獨(dú)立子集，使得V+-V+′中不存在滿足|Xi|≥x1的集團(tuán)Xi。

定義6[5]φ(x1,x2)表示p可取到的最大正整數(shù)。指的是在G+(V+,E+)中，對(duì)于V+中滿足|V+′|≤p的每一個(gè)子集V+′，V+-V+′是V+的獨(dú)立子集，則至少存在著一個(gè)屬于V+-V+′的集團(tuán)Xi，Xi滿足以下2個(gè)條件。

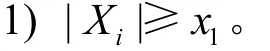
定義7[5]函數(shù)I(m)表示節(jié)點(diǎn)數(shù)為m的所有節(jié)點(diǎn)子集中，2個(gè)端點(diǎn)都屬于該子集的邊的最大數(shù)目。

由I(m)的定義可知，I(1)=0。

3 交換交叉立方網(wǎng)絡(luò)的拓?fù)湫再|(zhì)

接下來(lái)，對(duì)交換交叉立方網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)的鄰節(jié)點(diǎn)性質(zhì)展開(kāi)研究。

定理1設(shè)節(jié)點(diǎn)u和節(jié)點(diǎn)v是ECQ(s,t)中任意的2個(gè)節(jié)點(diǎn)，則N(u)∩N(v)≤2。

證明用數(shù)學(xué)歸納法證明。由圖 1～圖 3可知，ECQ(1,1)、ECQ(1,2)和ECQ(2,2)都滿足N(u)∩N(v)≤2。假設(shè)ECQ(s-1,t)(或者ECQ(s,t-1))也滿足N(u)∩N(v)≤2。接下來(lái)證明ECQ(s,t)是否滿足N(u)∩N(v)≤2。根據(jù)引理 2把ECQ(s,t)劃分為2個(gè)ECQ(s-1,t) (或者ECQ(s,t-1))，分別表示為L(zhǎng)和R。不失一般性，設(shè)當(dāng)u,v∈V(L)(或者u,v∈V(R))時(shí)，N(u)∩N(v)?V(L)(或者N(u)∩N(v)?V(R))。根據(jù)數(shù)學(xué)歸納法的假設(shè)可知|N(u)∩N(v)|≤2。而當(dāng)u∈V(L)并且v∈V(R)(或者u∈V(R)并且v∈V(L))時(shí)，如圖4所示，由于A和C之間是完美匹配，所以|N(u)∩N(v)|≤2。因此，定理1可證，證畢。

定理2設(shè)節(jié)點(diǎn)u和節(jié)點(diǎn)v是ECQ(s,t)中任意的2個(gè)節(jié)點(diǎn)，且(u,v)∈E(ECQ(s,t))，那么

證明由引理 1可知，ECQ(s,t)的所有節(jié)點(diǎn)中，c位置取值為 0的節(jié)點(diǎn)的度為(s+1)，c位置取值為1的節(jié)點(diǎn)的度為(t+1)。所以由引理5可知，當(dāng)u和v在c位置的取值都為0時(shí)，；當(dāng)u和v在c位置的取值都為1時(shí)，；當(dāng)u和v有一個(gè)在c位置的取值為 0，另一個(gè)在c位置的取值為 1時(shí)，。因此證畢。

在得到 ECQ(s,t)相關(guān)拓?fù)湫再|(zhì)的基礎(chǔ)上，對(duì) ECQ(s,t)在 PMC模型下的(t1,k)-診斷度展開(kāi)研究。

4 交換交叉立方網(wǎng)絡(luò)在PMC模型下的(t1,k)-可診斷

首先進(jìn)行函數(shù)?(x1)、φ(x1,x2)和I(m)的取值研究。

定理3在ECQ(s,t)中，

證明根據(jù)引理 2可把ECQ(s,t)劃分為 2個(gè)ECQ(s-1,t)，分別表示為L(zhǎng)和R，其中，V(L)=如圖4可知，節(jié)點(diǎn)集合A中的每一個(gè)節(jié)點(diǎn)都與節(jié)點(diǎn)集合C中的一個(gè)節(jié)點(diǎn)相鄰接。對(duì)于ECQ(s,t)的任意節(jié)點(diǎn)子集X和Y，設(shè)由于YL中的任意節(jié)點(diǎn)至多只有一個(gè)屬于YR的鄰節(jié)點(diǎn)，反之也一樣，因此存在著如式(1)所示的不等式。

Y內(nèi)部的邊數(shù)≤LY內(nèi)部的邊數(shù)+

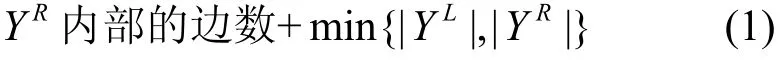
設(shè)IL(m)(或者IR(m))表示屬于L(或者R)且節(jié)點(diǎn)數(shù)為m的節(jié)點(diǎn)子集包含內(nèi)部邊的最大數(shù)目，同樣有IL(1)=0、IR(1)=0。由不等式(1)可知，I(|Y|)≤。不失一般性地，設(shè)則那么，

接下來(lái)，用數(shù)學(xué)歸納進(jìn)行證明。由圖1～圖3可知，ECQ(1,1)、ECQ(1,2)和ECQ(2,2)都滿足。假設(shè)ECQ(p,q)也有其中1＜p＜s、1＜q≤t。那么接下來(lái)證明ECQ(s,t)是否滿足

當(dāng)β=0時(shí)由歸納法的假設(shè)可知因此。當(dāng)β≥1時(shí)，，同樣由歸納法的假設(shè)可知設(shè)函數(shù)，可知f′(β)=由于，可知β=1或者時(shí)f()β可取到最大值。由于所以I(m)≤mlbm，定理3可證，證畢。

接下來(lái)，對(duì)ECQ(s,t)在PMC模型下滿足(t1,k)-可診斷時(shí)k和t1的取值進(jìn)行研究。

4.1 k的取值研究

給定癥候下的ECQ(s,t)用表示，其中1≤s≤t。設(shè)集團(tuán)XV+∈，VX表示X的節(jié)點(diǎn)集合，VN(X)表示X的鄰節(jié)點(diǎn)集合。由ECQ(s,t)和集團(tuán)的定義可知|X|＞0、|VN(X)|＞0，并且X具有以下性質(zhì)。

定理4把G(V,E)表示為G+(V+,E+)，設(shè)集團(tuán)X∈V+，則|VN(X)|≥k(G)或者

證明由X和VN(X)的定義可知，X和V-VN(X)之間不存在邊連接，如果V-VX-VN(X)≠?則VN(X)是G(V,E)的一個(gè)點(diǎn)割集，因此|VN(X)|≥k(G)。而當(dāng)V-VX-VN(X)=?時(shí)，可以直接推導(dǎo)出V=VX+VN(X)，證畢。

另外可知，從VN(X)發(fā)出的到VN(X)以外的邊數(shù)+VN(X)內(nèi)部的邊數(shù)≥VN(X)到VX的邊數(shù)+VN(X)到V-VX-VN(X)的邊數(shù)，如圖7所示。由引理1可知，ECQ(s,t)中每一個(gè)節(jié)點(diǎn)的度∈{s+1,t+1}。由于1≤s≤t，所以從VN(X)發(fā)出的到VN(X)以外的邊數(shù)+VN(X)內(nèi)部的邊數(shù)≤|VN(X)|(t+1)。VN(X)到VX的邊數(shù)=VX到VN(X)的邊數(shù)=VX發(fā)出的到VX以外的所有邊數(shù)－VX內(nèi)部的邊數(shù)，因此VN(X)到VX的邊數(shù)≥|VX|(s+1)-I(|VX|)。同理，由于V-VX-VN(X)與VX之間不存在著邊連接，所以VN(X)到V-VX-VN(X)的邊數(shù)。因此VX-VN(X)|)。由定理3可知所以可得

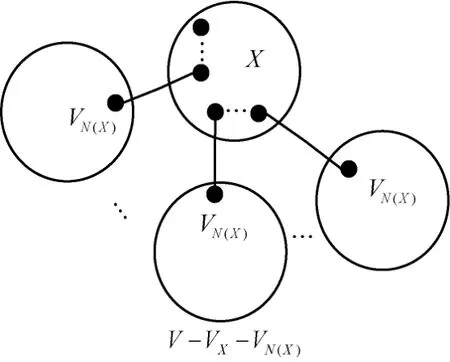
圖7 G+(V+,E+)中集團(tuán)X和VN(X)示意

由不等式(2)可進(jìn)一步推導(dǎo)出定理5。

定理5在給定癥候下，ECQ(s,t)用G+(V+,E+)表示，其中，1≤s≤t。那么對(duì)于V+中的任意集團(tuán)X，都有|VN(X)|≥s+1。

證明由于以下分2種情況進(jìn)行證明。

情況1|VX|≥2(s+1)并且|V-VX-VN(X)|≥2(s+1)，由于|V-VX-VN(X)|=|V|-|VX|-|VN(X)|，所以可推導(dǎo)出2(s+1)≤|VX|≤|V|-|VN(X)|-2(s+1)＜|V|-2(s+1)。因此，可知4(s+1)＜|V|。設(shè)p=|VN(X)|，q=|VX|，所以2(s+1)≤q≤|V|-p-2(s+1)＜|V|-2(s+1)。可以把不等式(2)轉(zhuǎn)換為

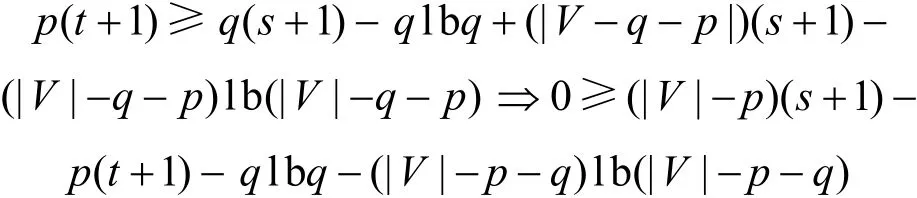
對(duì)函數(shù)h(p,q)求偏導(dǎo)，可得

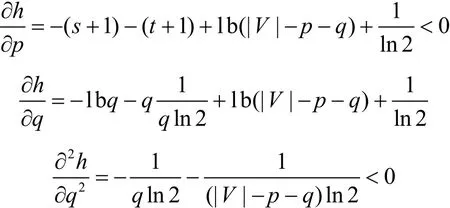
所以h(p,q)是關(guān)于變量p單調(diào)遞減，并且由h(p,q)的一階偏導(dǎo)和二階偏導(dǎo)可知，h(p,q)在p取最大值并且q取最大值(或者取最小值)時(shí)可以取到最小值。

假設(shè)p≤s+1，那么當(dāng)p=s+1并且q=2(s+1)(或者q=|V|-2(s+1))時(shí)h(p,q)可取到最小值。因此，h(s+1,2(s+1))≤h(p,q)，h(s+1,|V|-2(s+1))≤h(p,q)。由于h(s+1,2(s+1))＞0、h(s+1,|V|-2(s+1))≥0，所以要求h(p,q)＞0，這與h(p,q)≤0相矛盾。因此

情況2

情況2.1

情況2.1.1

情況2.1.2

由V≠VX+VN(X)，可知V-VX-VN(X)≠?。由定理 4可知，|VN(X)|≥k(G)。又由引理 4可知k(ECQ(s,t))=s+1，所以|VN(X)|≥s+1。

情況2.2

證畢。

由引理10和定理5可知，對(duì)于給定癥候下的ECQ(s,t)，如果可以確定集團(tuán)X是正確集團(tuán)，那么可知VN(X)都是故障節(jié)點(diǎn)，且|VN(X)|≥s+1。因此，在能確定任意一個(gè)正確集團(tuán)的前提下，ECQ(s,t)在PMC模型下滿足(t1,k)-可診斷時(shí)k≥s+1。

4.2 t1的取值研究

首先研究ECQ(s,t)中函數(shù)?(t1+1)的取值，在此基礎(chǔ)上研究滿足φ(t1+1,0)≥t1時(shí)t1可取到的最大值，進(jìn)而可以確定ECQ(s,t)在 PMC模型下滿足(t1,k)-可診斷時(shí)t1的取值。

定理6對(duì)于ECQ(s,t)，函數(shù)?(t1+1)≥其中1≤s≤t。

證明根據(jù)?(x1)的定義可知?(t1+1)≥，表示存在著一個(gè)滿足的集團(tuán)子集V′+，使V+-V+′是V+的獨(dú)立子集，并且V+-V+′中的任意集團(tuán)Yj都滿足|Yj|≤t1。設(shè)其中X,X,…,X及12a表示V+中所有的集團(tuán)，

由于V+-V+′是V+的獨(dú)立子集，所以集團(tuán)兩兩不相鄰且由引理1可知，ECQ(s,t)中c位置取值為0的節(jié)點(diǎn)的度為s+1，c位置取值為1的節(jié)點(diǎn)的度為t+1，其中1≤s≤t。因此，，其中，且V+′與V+-V+′之間的邊數(shù)目不超過(guò)（當(dāng)從V′+發(fā)出的所有邊的另一個(gè)頂點(diǎn)都屬于V+-V+′時(shí)可取到最大值）。

由于

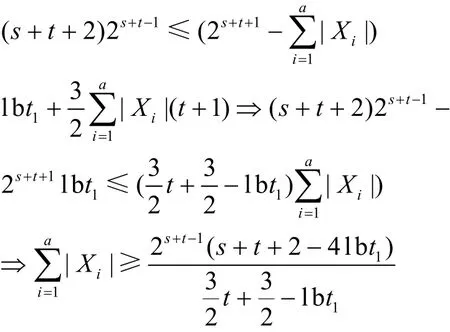
定理6可證，證畢。

基于?(t1+1)和φ(t1+1,0)的關(guān)聯(lián)關(guān)系，可通過(guò)定理6對(duì)φ(t1+1,0)≥t1時(shí)t1的取值進(jìn)行研究，得出定理7。

定理 7對(duì)于時(shí)函數(shù)其中0≤δ＜1。

證明由于所以接下來(lái)，需要證明是否成立。設(shè)，可以求得。可知當(dāng)時(shí)時(shí)h(t1)單調(diào)遞減。且當(dāng)時(shí)h(t1)＜0，h(t1)的基本走勢(shì)如圖 8所示。 由于時(shí)存在著，因此根據(jù)的定義可知，時(shí)不滿足。而當(dāng)時(shí)為了使，則要求同時(shí)可知時(shí)。因此，其中0≤δ＜1。定理7可證，證畢。

圖8 h(t1)的走勢(shì)

由定理7可知，ECQ(s,t)在PMC模型下滿足-可診斷時(shí)，如果，其中0≤δ＜1，那么至少存在著一個(gè)集團(tuán)Xi，|Xi|≥t1+1且|N(Xi)|≥0。根據(jù)(t1,k)-可診斷的定義可知系統(tǒng)的故障節(jié)點(diǎn)數(shù)不超過(guò)t1時(shí)集團(tuán)Xi必然是正確集團(tuán)，VN(Xi)是故障節(jié)點(diǎn)。

4.3 交換交叉立方網(wǎng)絡(luò)在 PMC 模型下的(t1,k)-診斷度

由于k=t1時(shí)(t1,k)-可診斷就是一步t1-可診斷，ECQ(s,t)在k=t1時(shí)的(t1,k)-診斷度如定理 8所示。

定理8ECQ(s,t)滿足(s+1,s+1)-可診斷，其中1≤s≤t。

證明由引理4可知，1≤s≤t時(shí)k(ECQ(s,t))=s+1。由于1)+1，其中1≤s≤t。由引理7可知，ECQ(s,t)是一步(s+1)-可診斷，因此ECQ(s,t)滿足(s+1,s+1)-可診斷，其中1≤s≤t，定理8可證，證畢。

根據(jù)定理5和定理7可進(jìn)一步證得ECQ(s,t)在t1＞k時(shí)的(t1,k)-診斷度，如定理9所示。

定理 9ECQ(s,t)滿足-可診斷，其中

證明由定理7可知，ECQ(s,t)在PMC模型下滿足(t1,k)-可診斷時(shí)，如果其中0≤δ＜1，那么至少存在著一個(gè)集團(tuán)Xi，|Xi|≥t1+1且|N(Xi)|≥0。又由定理 5可知，給定癥候下ECQ(s,t)的任意集團(tuán)Xi∈V+，都有|VN(Xi)|≥s+1，其中1≤s≤t。因此，根據(jù)(t1,k)-可診斷的定義可知ECQ(s,t)是可診斷系統(tǒng)，其中。證畢。

4.4 仿真實(shí)驗(yàn)

接下來(lái)，對(duì)ECQ(s,t)（1≤s≤t≤5）的(t1,k)-診斷度進(jìn)行仿真實(shí)驗(yàn)驗(yàn)證。仿真算法分為節(jié)點(diǎn)編碼處理、節(jié)點(diǎn)狀態(tài)編碼處理和(t1,k)-診斷度計(jì)算3個(gè)模塊。通過(guò)節(jié)點(diǎn)編碼處理模塊和節(jié)點(diǎn)狀態(tài)編碼處理模塊分別賦給每一個(gè)節(jié)點(diǎn)一個(gè)地址值和一個(gè)狀態(tài)值，其中，地址值用一個(gè)長(zhǎng)度與維數(shù)相等的二進(jìn)制數(shù)表示，狀態(tài)值用一位二進(jìn)制表示，如圖9所示。

以ECQ(2,2)為例，其拓?fù)浣Y(jié)構(gòu)如圖3所示，共有節(jié)點(diǎn)數(shù)32個(gè)，所有節(jié)點(diǎn)的地址值用一個(gè)長(zhǎng)度為5的二進(jìn)制表示，通過(guò)節(jié)點(diǎn)編碼處理模塊生成的節(jié)點(diǎn)地址值如表2所示。

節(jié)點(diǎn)有正常和故障2種狀態(tài)，用“0”表示“正常”狀態(tài)，用“1”表示故障狀態(tài)。以ECQ(2,2)為例，通過(guò)節(jié)點(diǎn)狀態(tài)編碼處理模塊之后，32個(gè)節(jié)點(diǎn)的狀態(tài)值總共有232種情況，如表3所示。仿真實(shí)驗(yàn)并不需要考慮232種的所有的情況，只需要根據(jù)t的取值，考慮故障節(jié)點(diǎn)數(shù)少于等于t個(gè)的情況，因此共有Ct32種情況。

(t1,k)-診斷度計(jì)算處理模塊按照引理 6的充要條件進(jìn)行設(shè)計(jì)，包含3個(gè)步驟，具體如下。

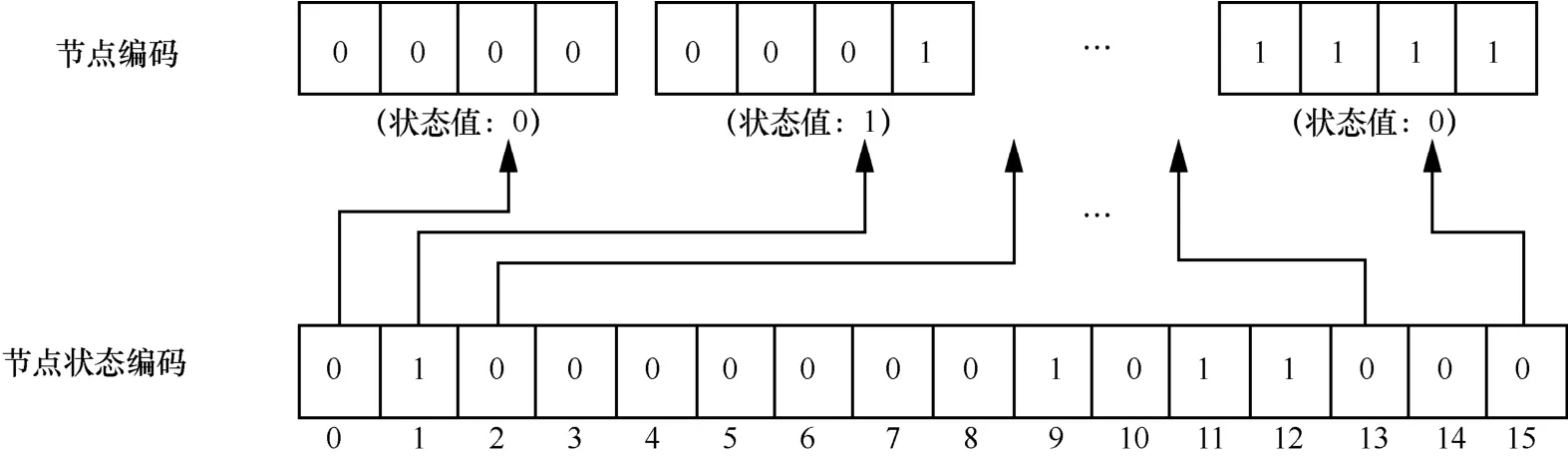
圖9 仿真實(shí)驗(yàn)的節(jié)點(diǎn)編碼和節(jié)點(diǎn)狀態(tài)編碼

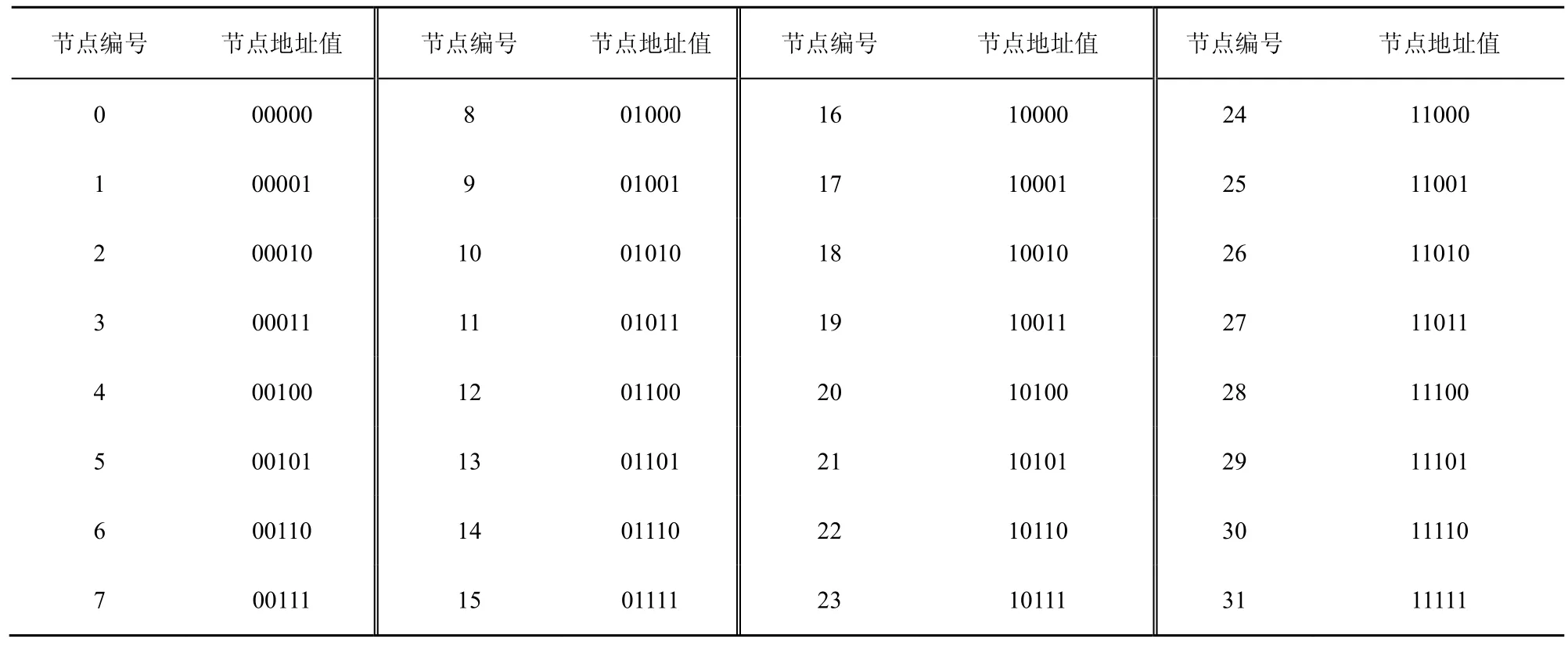
表2 ECQ(2, 2)中32個(gè)節(jié)點(diǎn)的地址值

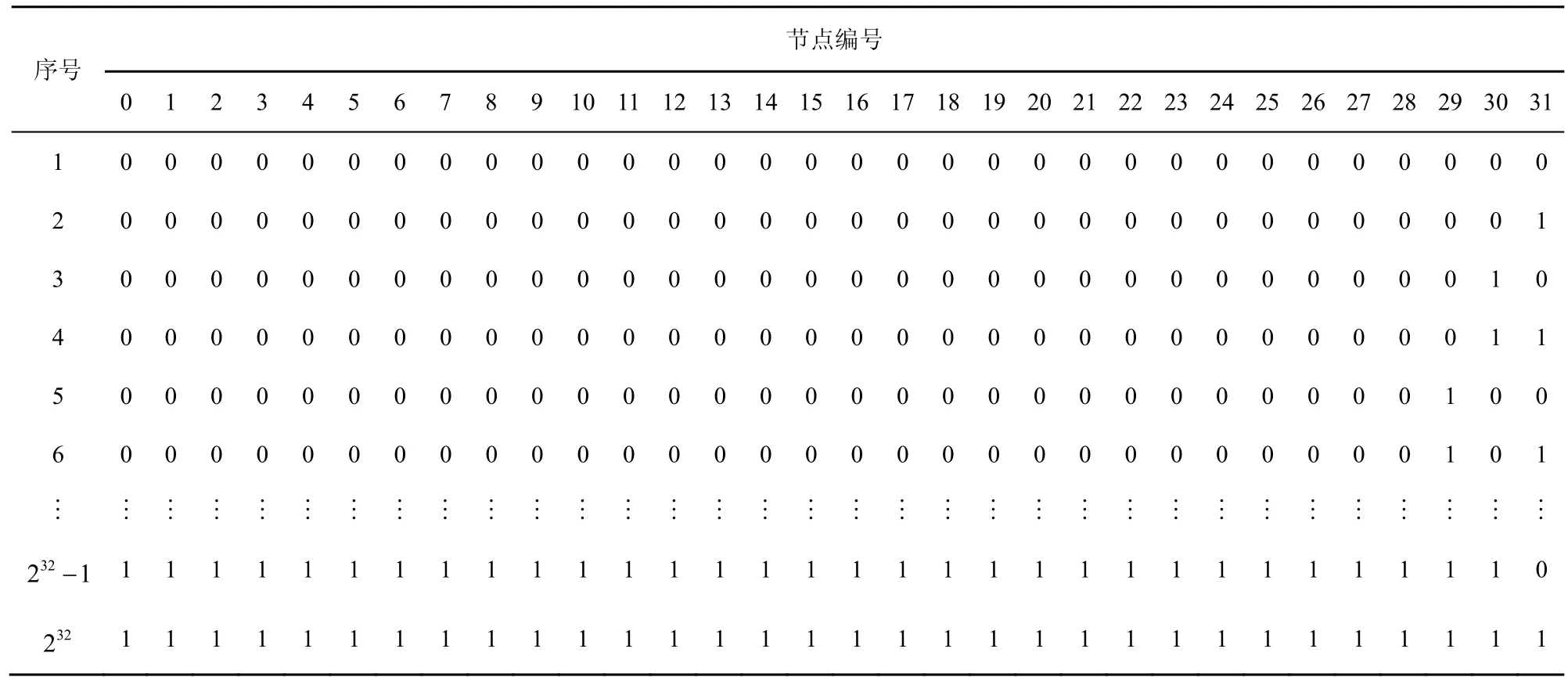
表3 ECQ(2, 2)中32個(gè)節(jié)點(diǎn)可取的狀態(tài)值

步驟1計(jì)算出ECQ(s,t)中不超過(guò)t1個(gè)故障節(jié)點(diǎn)的所有故障節(jié)點(diǎn)集合。

步驟 2對(duì)每一種故障節(jié)點(diǎn)集合的每一個(gè)癥候σ，構(gòu)建出Ωσ,t1。

步驟3如果所有故障節(jié)點(diǎn)集合的所有癥候都滿足或者那么ECQ(s,t)滿足(t1,k)-可診斷，否則t1=t1-1，跳轉(zhuǎn)到步驟 1。

以ECQ(2,2)為例，步驟 1中不超過(guò)t（t≥1）個(gè)故障節(jié)點(diǎn)的所有故障節(jié)點(diǎn)集合共有（即 35 960）種。設(shè)定t=4之后，故障節(jié)點(diǎn)集合共有種情況，如表4所示。

進(jìn)而以第5 178種情況的故障節(jié)點(diǎn)集合為例構(gòu)建起癥候，如圖10所示。

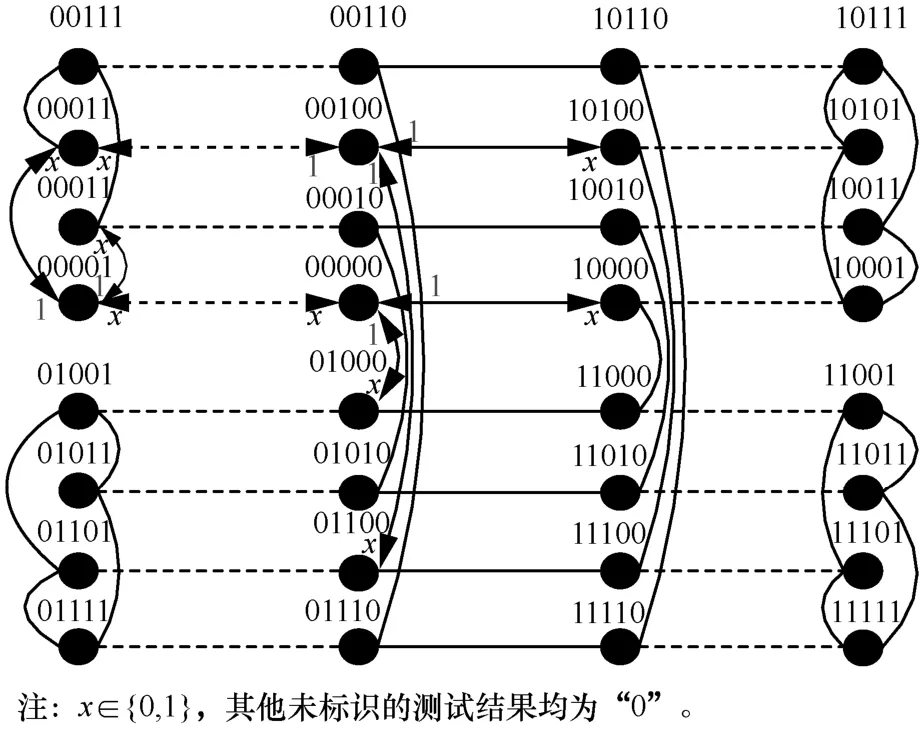
圖10 ECQ(2,2)特定癥候

與圖10癥候相一致的故障節(jié)點(diǎn)集合，只有表5所示的唯一一種情況。因此，Ωσ,t={00000, 00001,00010}。

節(jié)點(diǎn)編碼處理模塊和節(jié)點(diǎn)狀態(tài)編碼處理模塊的處理流程相對(duì)簡(jiǎn)單，計(jì)算規(guī)模較小。仿真實(shí)驗(yàn)的主要處理過(guò)程集中在(t1,k)-診斷度計(jì)算處理模塊，通過(guò)步驟 1可以取得種故障節(jié)點(diǎn)集合，在最壞情況下步驟 2中的每一種故障節(jié)點(diǎn)集合最多需要對(duì)應(yīng)2t1個(gè)癥候，最后通過(guò)步驟 3進(jìn)行循環(huán)判斷。仿真實(shí)驗(yàn)的時(shí)間復(fù)雜度為O(2nt1)，時(shí)間復(fù)雜度較高。仿真實(shí)驗(yàn)環(huán)境為2顆至強(qiáng)E5-4620 v2 CPU，2塊16 GB 1 600 MHz內(nèi)存，2塊1.2 TB 10K RPM SAS 6 Gbit/s硬盤(pán)，Microsoft SQL Server 2008數(shù)據(jù)庫(kù)。通過(guò)計(jì)算得出的仿真實(shí)驗(yàn)數(shù)據(jù)如表6所示。實(shí)驗(yàn)結(jié)果進(jìn)一步印證了定理7和定理8的結(jié)論。

實(shí)際應(yīng)用中可以引入環(huán)診斷算法[22]進(jìn)行(t1,k)-故障診斷。根據(jù)環(huán)診斷算法，對(duì)初始癥候進(jìn)行局部識(shí)別，借助0→0→…→0→1的局部癥候來(lái)識(shí)別故障節(jié)點(diǎn)，進(jìn)而在替換掉已識(shí)別故障節(jié)點(diǎn)的基礎(chǔ)上進(jìn)行第二次迭代故障診斷，直到所有的故障節(jié)點(diǎn)都被識(shí)別為止。

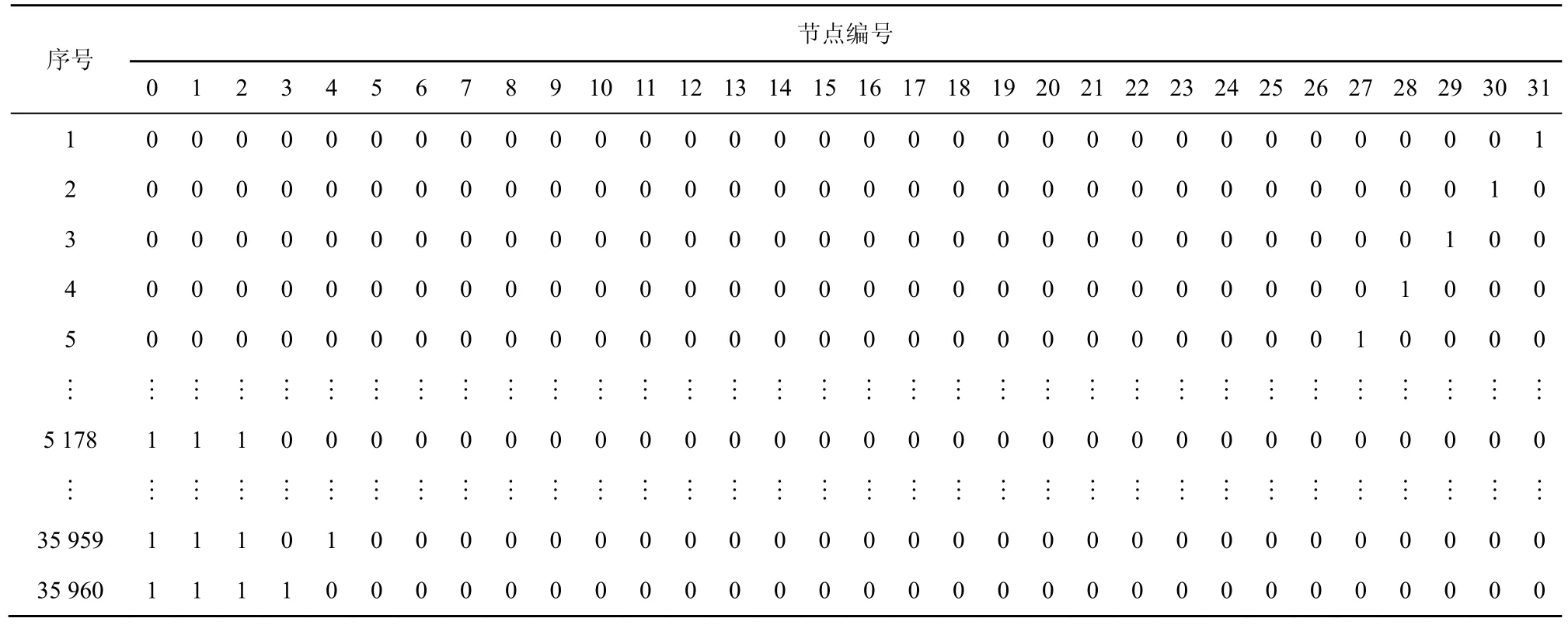
表4 故障節(jié)點(diǎn)數(shù)不超過(guò)4時(shí)ECQ(2, 2)的35 960種故障節(jié)點(diǎn)集合

表5 與圖10癥候相一致故障節(jié)點(diǎn)集合

5 結(jié)束語(yǔ)

本文以ECQ(s,t)為研究對(duì)象，首先對(duì)ECQ(s,t)的拓?fù)浣Y(jié)構(gòu)展開(kāi)研究，證得了ECQ(s,t)在鄰節(jié)點(diǎn)方面的相關(guān)拓?fù)湫再|(zhì)。在此基礎(chǔ)上引入集團(tuán)的思想，借助3個(gè)重要函數(shù)證明了ECQ(s,t)在PMC模型下是(s+1,s+1)-可診斷和可診斷，其中最后通過(guò)仿真實(shí)驗(yàn)驗(yàn)證了結(jié)論的正確性。本文的研究成果將有利于進(jìn)一步理清交換交叉立方網(wǎng)絡(luò)的可靠性，為交換交叉立方網(wǎng)絡(luò)的應(yīng)用和推廣奠定了堅(jiān)實(shí)的理論基礎(chǔ)。

表6 仿真實(shí)驗(yàn)數(shù)據(jù)與理論推導(dǎo)結(jié)果