一種基于密度聚類的分布式離群點檢測算法?

劉亞梅 閆仁武

（江蘇科技大學計算機學院 鎮江 212003）

1 引言

局部離群點檢測算法是數據挖掘中離群點檢測的一個重要研究方向。基于小規模數據集的挖掘，離群點往往是被作為噪聲除去的，但隨著數據規模的不斷擴大，大數據技術的日益成熟，從海量數據中挖掘的離群點可不再是噪聲和無用點，這些點可以揭示稀有事件和現象、發現有用的信息，成為有意義點。Hawkins［1］的關于離群點的定義得到廣泛認可，在相關的研究領域，局部離群點檢測算法［2］已經相當成熟，但是面對大量高維的復雜數據時，這些算法的執行效率、檢測準確度等方面還存在明顯的不足。

迄今，諸多學者采用了許多方法來提高離群檢測算法的性能。例如，張天佑［3］提出基于網格劃分的高維大數據集離群點檢測算法，將高維空間進行網格劃分后，對剩余離群點集進行檢測，缺點是對高維海量數據進行網格劃分時，時效將成指數增長；周鵬等［4］提出一種結合平均密度的改進LOF 異常點檢測算法，先根據數據集中數據點的平均密度的分布情況確定的一個異常集D1，然后通過計算離群因子確定另一個個異常點及異常集D2，取D1與D2的交集作為最終的離群集，缺點是對于海量數據來說，其計算效率也會很低；王習特等［5］提出一種高效的分布式離群點檢測算法，運用DBSP（Balance Driven Spatial Partitioning）數據劃分算法對數據進行預處理，提出了BOD（DBSP-Based Outlier Detection）分布式離群點檢測算法，但算法對全局離群點有良好的檢測效率，不適用于局部離群點的檢測。

Google 提出的MapReduce 是一種用于大規模數據集的并行運算編程模型，能夠處理T 級別以上巨量數據的業務［7］。Apache 基金會開發的Hadoop分布式系統能夠很好地處理巨量數據，本文中基于Hadoop 平臺，應用MapReduce 編程模型實現了一種局部離群點檢測算法——基于密度聚類（DBSCAN）的局部離群點檢測算法（LOF）。首先根據文獻［5］DBSP數據劃分算法對數據進行預處理，使得各數據對象均勻的劃分到各個運行節點（DataNode）上；然后基于DBSCAN 密度聚類對數據塊中數據進行聚類后剪枝優化，得到小規模的初始離群數據集；最后計算其局部離群因子［8］（LOF）來確定離群檢測結果，從而提高算法的運行效率和準確率。

2 相關理論

2.1 密度聚類算法DBSCAN

DBSCAN 算法是基于一組鄰域參數（?，MinPts）來描述樣本分布的緊密程度的一種算法。給定數據集D={x1，x2，…，xm} ，包含m 個樣本，每個樣本xi=(xi1;xi2;…;xin)是一個n 維特征向量，其中m，n，i為正整數，定義如下概念［10～11］。

定義1?-鄰域：對xj∈D，其?-鄰域包含樣本集D 中與xj的距離不大于?的樣本，即N?(xj)={xi∈D|dist(xi，xj)≤?}，其中j為正整數；

定義2 核心對象：若xj的?-鄰域至少包含MinPts個樣本，即|N?(xj)|≥MinPts，則xj是一個核心對象；

定義3 密度直達：若xj位于xi的?-鄰域中，且xi是核心對象，則稱xj由xi密度直達；

定義4 密度可達：對xj與xi，若存在樣本序列p1，p2，…，pn，其中p1=xi，pn=xj且pi+1由pi密度直達，則稱xj由xi密度可達；

定義5 密度相連：對xj與xi，若存在xk使得xj與xi均由xk密度可達，則稱xj與xi密度相連；

定義6 簇：由密度可達關系導出的最大的密度相連樣本集合，即給定領域參數（?，MinPts），簇C∈D是滿足以下性質的非空子集：

1）連接性：xi∈C，xj∈C?xj與xi密度相連；

2）最大性：xi∈C，xj由xi密度可達?xj∈C。

綜上所述，若xi為核心對象，由xi密度可達的所有樣本組成的集合記為X(i)={xj∈D|xj由xi密度可達}為滿足連接性與最大性的簇。以圖1 為例，給出了上述概念的直觀顯示。其中：MinPts=3，虛線表示?-鄰域，x1是核心對象，x2由x1密度直達，x3由x1密度可達，x3與x4密度相連。

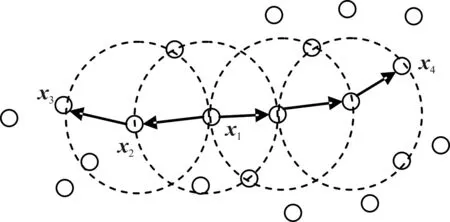
圖1 DBSCAN定義的基本概念

其中對任意兩個樣本點xi和xj有：xi=(xi1，xi2，…，xin)和xj=(xj1，xj2，…，xjn)。xi和xj是n維屬性空間的兩個樣本點且xi≠xj，它們之間的距離（歐氏距離）計算定義如下：

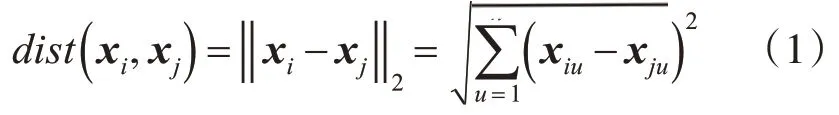
通常距離的計算還有以下幾種：曼哈頓距離、閔可夫斯基距離、內積距離、余弦距離等，當數據對象的不同屬性的重要性不同時，還可使用加權距離，利用權重ωi表征不同屬性的重要性。聚類結束后生成的簇劃分C={C1，C2，…，Ck}，定義：

定義7 簇Cl的中心點，其中l為正整數，|Cl|為簇Cl的樣本數：

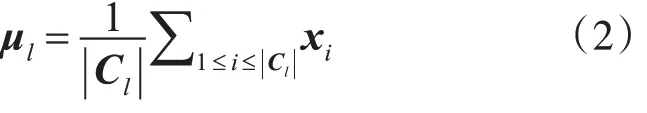
定義8 簇Cl內樣本間的平均距離：

定義9 簇Cl內樣本間的最遠距離：

定義6簇Cl與簇Cm最近樣本間的距離：

定義10 簇Cl與簇Cm中心點間的距離：

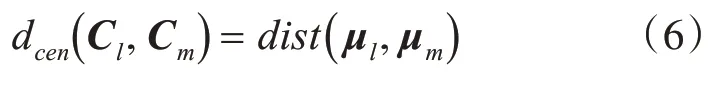
2.2 局部離群點檢測算法LOF

通常情況下，離群點分為全局離群點和局部離群點兩種類型，基于統計和基于距離的離群點檢測算法適用于全局離群點的檢測。通過對基于距離的檢測方法的改進，Breunig 提出了基于密度的離群檢測方法［8］，該方法提出基于密度的局部離群因子（LOF）概念作為離群度量，很好地解決了局部離群點的檢測問題。對于任意樣本點y且y∈D，算法的幾個定義如下［12］：

定義11y的k-距離：數據集中到數據樣本對象y距離最近的第k 個點到y的距離，記作k(y)其中k為自然數，這里的距離指歐式距離。

定義12y的k距離鄰域Nk(y)：數據集中與與數據樣本對象y的距離不大于k(y)的數據點組成的集合。

定義13y相對于s（s∈D且s≠y）的可達距離：

如果樣本y遠離樣本s，則其可達距離就是它們之間的實際距離，如果二者足夠近，則可達距離為y的k-距離。

定義14y的局部可達密度：

如果y是局部離群點的程度越小，則LOFk(y)值接近于1，即y不是局部離群點。相反，若y是局部離群點的程度越大，所得的LOFk(y)值越高。

2.3 分布式平臺理論

Hadoop平臺主要由MapReduce、HDFS、HBase、Hive 等項目組成。其中MapReduce 用于大規模數據集（大于1TB）的并行運算，其核心理念是將一個大的運算任務分解到集群每個節點上，充分運用集群資源，縮短運行時間［16］；HDFS是一個分布式文件系統，它通過將一個大的文件劃分成一個個固定大小Block 來實現分布式存儲［17］，目前HBase 的所有底層數據都以文件的形式交由HDFS 來存儲；HBase 是一個分布式、按列存儲的數據庫［6］。其結構是以key-value 作為一行數據，可以隨機訪問、實時讀取，對表中未存在的列和列簇不做存儲，既節省空間，同時提高讀寫效率。本文在算法實現的機制中采用Hbase數據庫和MapReduce模型。

MapReduce 模型分為Map 任務和Reduce 任務兩個階段。每一個MapReduce 作業執行時都會拆分成Map 和Reduce 兩個階段：Map 對應輸入值key，value經處理后生成中間輸出值key′，value′并作為Reduce 階段的輸入值，Reduce 對相同key'下的所有value'進行處理最后生成key′，value′ 作為最終結果。其流程如圖2。

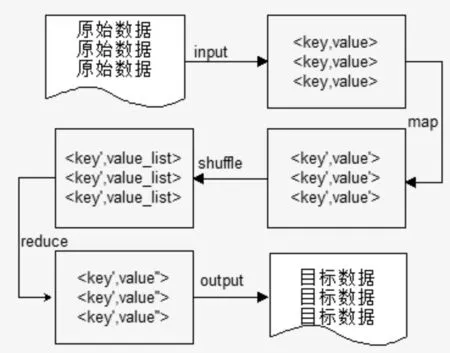
圖2 MapReduce流程

3 本文算法

典型的基于密度的LOF 算法的核心思想是為每個數據對象賦予了表征其離群程度的離群因子，然后計算每個對象的離群度，并根據離群度排序，最后取其前若干個點作為離群點。相關的改進算法大多都是從距離度量方面以及最終離群因子的計算方面改進［4］。本文針對數據集的規模和距離度量方面借鑒前人的算法進行改進，在數據預處理階段通過文獻［5］DBSP算法將數據均勻劃分后，利用DBSCAN聚類算法將大多數正常數據對象去除，從而削減數據集的規模，生成初始離群數據集，為保證數據集的整體特性不變，對LOF算法進行了相應的改進，最終找出離群點的集合。

3.1 基于密度聚類的離群點檢測算法

3.1.1 基于DBSCAN算法的數據預處理

Hadoop 分布式系統對數據集隨機分塊，這一過程對離群點檢測的準確率存在一定的誤差，為了減小這一誤差，采用文獻［5］DBSP數據劃分算法對數據進行預處理，使得數據能均勻的劃分到各個數據塊中。DBSCAN 算法的時間復雜度為O(nlogn)相對較低，能夠處理任何大小和形狀的簇。所以利用DBSCAN 算法來對海量的復雜數據集進行剪枝處理是很好的。DBSCAN算法具體算法描述下：

輸入：數據集D，鄰域參數（?，MinPts）

輸出：簇劃分C={C1，C2，…，Ck}的中心點，包括各簇的平均距離、最大距離。

算法過程：

1）確定鄰域參數（?，MinPts），根據式（1），定義1確定數據對象xj的?-鄰域N?(xj)；

2）如果|N?(xj)|≥MinPts那么將樣本xj加入核心對象集合：O=O∪{xj} ；

3）隨機選取一個核心對象o∈O，找出所有從該點密度可達的對象，形成一個類簇；

4）重復步驟2）、3）直到形成聚類簇劃分C={C1，C2，…，Ck}；

5）利用式（3）、式（4）分別計算各簇Cl的平均距離avg(Cl)，最大距離diam(Cl)；

6）利用式（2）分別計算各簇的中心點μ={μ1，μ2，…，μk} 保留中心點作為各簇的代表；

7）輸出：初步離群數據集D′=DC∪μ。

3.1.2 改進的LOF算法實現

數據集D經過數據預處理之后，剪掉大部分正常的數據對象，縮小了數據集的容量，形成初步離群數據集D′。為了確保數據的分布特性，提高算法的準確率，數據集D′中保留了聚類后各簇的中心點。由離群點的定義可知，類簇內的點不會是離群點，所以為了避免這些中心點被選為離群點，對LOF算法計算可達距離時進行了適當的改進，取權值ω=0.618 為中心點加權，使之不可能成為離群點。具體改進后的算法描述如下：

輸入：d維數據集D′，k，離群因子閾值ξ

輸出：離群點集合E

算法過程：

1）計算任意對象y（y∈D′）的k-距離k(y)并找出y的距離鄰域Nk(y)

2）計算y相對于s（s∈D且s≠y）的可達距離，其中對象y，s要分類討論來調整可達距離。

（1）若對象y，s都不是中心點，則可達距離由式（7）計算出reach_dist(y，s)；

（2）若對象y，s均是簇Cl和Cm的中心點，則可達距離為

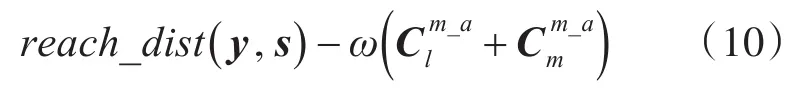
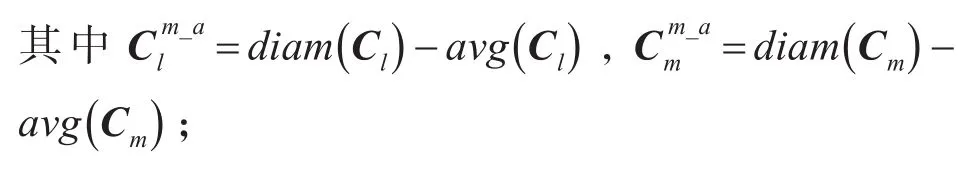
（3）若對象y，s只有一個是簇Cl的中心點，則可達距離為

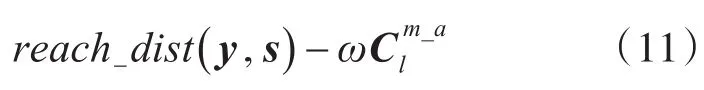
3）利用式（8）和步驟2）的改進計算各對象的局部可達密度。

4）利用式（9）計算各對象的局部離群因子。

5）若某個對象的離群因子LOF 值大于給定的閾值ξ，則輸出。

3.2 基于密度聚類的離群點檢測算法并行化

Hadoop 支持多種方式作為數據輸入源，本文采用HBase作為分布式數據庫，存儲數據源。算法步驟如下：

第1 步輸入原始數據集D，使用DBSP 算法確定數據集的均勻劃分，將數據塊存入DataNode 節點中。

第2 步由步驟1 產生的數據塊構建鍵值對K，V，K值表示所取的行號，V表示此行的字符串內容。Map 階段不做處理，在Reduce 階段將數據過濾，提取屬性值，輸出id，property，id值表示數據對象xi的唯一標識id，property表示數據對象xi的各個屬性值{xi1;xi2;…;xin} ，并存入輸出文件中。

第3 步輸入第2 步處理過的鍵值對id，property，在Map 階段不作處理，在Reduce 階段根據式（1）計算所有對象xi與其他對象的距離dist(xi，xj)，輸出鍵值對id，dist，dist中表示xi的與其他對象的距離dist(xi，xj)值，并存入輸出文件中。

第4 步輸入第3 步產生的鍵值對id，dist，Map 階段不作處理，在Reduce 階段計算出xi的?-鄰域，輸出鍵值對id，neighbor，其中neighbor表示每個數據對象xi的?-鄰域N?(xi)。

第5 步輸入第4 步產生的id，neighbor，Map階段根據根據3.1.1 節算法過程（1）～（2）確定核心對象集O，在Reduce 階段根據3.1.1 節算法過程（3）～（4）確 定 簇 劃 分C={C1，C2，…，Ck} ，輸 出

d，object，其中d 表示簇類號，object表示簇中對象，

第6 步輸入第5 步產生的鍵值對d，object，Map 階段融合第2 步產生的鍵值對，根據3.1.1 節算法過程5）利用式（3）、式（4）分別計算各簇Cl的平均距離avg(Cl)，最大距離diam(Cl)，在Reduce 階段根據3.1.1節算法過程6）～7）根據式（2）找出各簇的中心點μ={μ1，μ2，…，μk} ，確定初步離群數據集D′=DC∪μ，輸出D′_id，C_core。其中，D′_id表示初步離群數據對象id，C_core表示是否是簇的中心點、簇的平均距離和最大距離，并存入輸出文件中。

第 7 步輸入第 6 步產生的鍵值對D′_id，C_core，Map 階 段 融 合 第3 步 產 生 的id，dist，根據3.2.2 節算法過程1）產生各對象的距離鄰域，在Reduce 階段根據3.2.2 節算法過程2）計算各對象的可達距離，輸出D′_id，reach其中D′_id表示每個數據對象的id，reach表示對象的可達距離。

第 8 步輸入第 7 步產生的鍵值對D′_id，reach，在Map 階段根據3.2.2 節算法過程3）計算各對象的局部可達密度，在Reduce 階段根據3.2.2 節算法過程4）計算各對象的局部離群因子，輸出鍵值對D′_id，lof，其中lof表示數據對象的局部離群因子。

第9 步輸入第8 步產生的鍵值對D′_id，lof，在Map階段不作處理。在Reduce階段根據3.2.2節算法過程5），找出離群對象，輸出鍵值對Outlier_id，Outlier_lof，其中Outlier_id表示離群對象的id，Outlier_lof表示離群對象的離群因子。

4 實驗結果與分析

本文實驗所采用硬件環境：內存4.00GB，處理器Intel（R）Core（TM）i5-4590 CPU @ 3.30GHz 3.30 GHz。軟件環境：四臺機器安裝CentOS7.0 操作系統，Hadoop 生態環境采用Hadoop-2.6.0，HBase-1.0.1.1，Zookeeper-3.4.6，JDK-1.8.0_25，集成開發環境采用Eclipse。

實驗所用數據為網絡入侵檢測數據集KDD-CUP1999 數據集，該數據集中的數據對象分為5 大類，包括正常的連接、各種入侵和攻擊等。KDD99 數據集總共由500 萬條記錄構成，共41 維屬性，該數據集提供了一個10%的訓練子集和測試子集，為了進行實驗，對非數值屬性維進行數值化處理。隨機抽取4類異常類型數據30萬條，并加入正常數據10、20、30、40 條作為離群數據，進行算法驗證，并與傳統的LOF算法，文獻［4］提出的算法和本文提出的GJLOF 算法進行比較。檢測結果如表1所示。

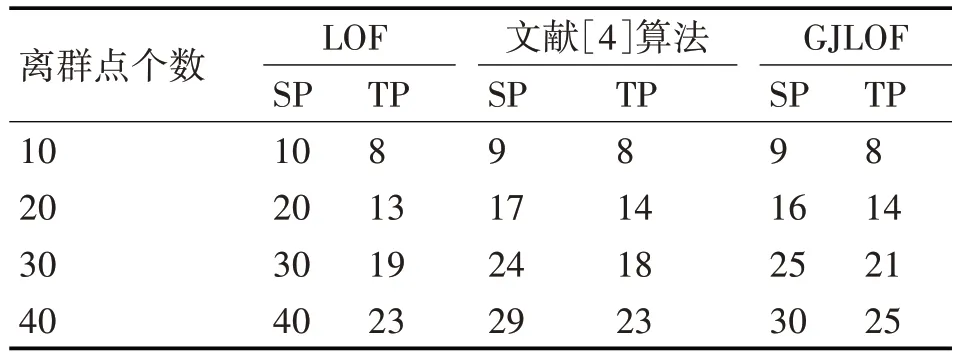
表1 各算法檢測結果

其中SP：檢測出的總數，TP：檢測出正確的個數。

1）使用離群點檢測精度衡量算法性能

圖3 各算法精確度比較

2）使用計算時間復雜度衡量算法性能

本節實驗用于評估本文算法的時間性能。分別從KDD99 數據集中選取不同規模的數據作為實驗數據集，然后在這些數據集上分別運行LOF、文獻［4］提出的算法和本文算法GJLOF。圖4 給出了實驗結果。隨著數據規模的不斷增加，本文算法的運行時間更低；相同數據規模下，本文算法運行時間相對較少。

圖4 各算法運行時間比較

3）數據可擴展性實驗

隨著數據規模的不斷增加，對于分布式系統來說，數據節點的數量同樣影響算法的運行效率。采用相同的實驗環境，依照節點的數量不同啟動1～3臺DataNode 節點機，并將數據集KDD99 處理加工成1Million、5Million、10Million 三種規模的數據進行實驗，對不同規模的數據都重復實驗三次，取平均值作為最終結果。由于硬件和網絡環境會造成Hadoop 集群節點的運算和通信差別，因此采用運行時間比R=t1作為指標量，其中t1為集群節點數量為1 的運行時間，n 為集群節點數。具體結果如圖5。

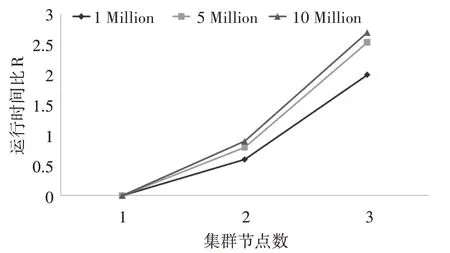
圖5 集群運行時間

根據圖5 的實驗結果可以看出，隨著集群節點的增多，相同規模數據集的計算效率有所提高，并且不同規模的數據集，數據規模越大，節點數量的變化對計算效率越明顯。

5 結語

本文提出了一種基于密度聚類的分布式離群點檢測算法，算法首先采用密度聚類算法，實現對數據規模的約簡，然后根據計算出的局部可達密度和局部離群因子，最終找出離群點。從實現機制上采用Hadoop 平臺上的MapReduce 模型框架，以HBase 作為數據庫，解決了算法的數據規模過大的問題。本文算法通過對數據集規模上的約簡，解決了離群點檢測算法計算量較大的問題，運行效率明顯提高，通過改進LOF 算法的可達距離，提高了準確率，但是由于對數據進行并行化操作時導致數據集聚類效果受到影響，并且算法對參數（?，MinPts）和k距離參數比較敏感，未來可以在解決數據均勻劃分和參數問題上進行研究。