城市密集人群疏散算法設計研究?

莫樂群

（廣東交通職業技術學院 廣州 510650）

1 引言

隨著社會經濟發展，公共場所高度集約化和規模化建設給公共安全帶來重大隱患，一旦發生事故容易造成群死群傷事件。如何在最短時間內有效疏散密集人群，讓人群組織有目的、有計劃逃離事故現場，是目前公共安全研究的重點和難點。

行人遭遇突發事件過度恐慌，出于逃生本能會出現推搡、踩踏等事件［1～3］。受疏散群體影響以及個體心理和生理差異，個體行為表現出一定的趨眾性和不確定性，因此行人流是一種極其復雜而又特殊的非線性物理運動。傳統宏觀行人流建模中把疏散速度與行人之間影響看成線性關系并不適宜［4～5］。微觀行人流建模有社會作用力模型、磁場引力模型、格子氣模型、元胞自動機模型等。其中元胞自動機模型將疏散個體描述為元胞，通過不同元胞相互作用和動態演化模擬人的個體行為和群體效應，目前已被廣泛應用于行人流理論和疏散建模研究。

元胞自動機模型由元胞、元胞空間、鄰居和演變規則四部分組成。其中，演化規則是行人流建模的核心，對人群疏散模擬有重大影響，直接決定疏散效率和人員傷亡情況。由于元胞狀態更新策略由元胞自身位置和鄰居元胞狀態共同決定［6～7］，這與粒子群PSO 算法中鳥類尋找全局最優值思想一致［8～9］。文章將元胞狀態更新轉變為策略優化問題，通過求解適應值函數計算元胞全局最優演化規則，從而提高疏散效率，減少人員傷亡的目的。

2 元胞自動機模型

元胞自動機模型是一種時空離散的動力演化系統。網格中每一個元胞選取有限離散狀態，并遵循相同演化規則更新當前狀態［10］。所有元胞根據自身和周圍元胞狀態相互作用［11～12］，共同構成動態系統演化。元胞自動機模型由元胞、元胞空間、鄰居和演變規則四部分組成［13～15］。定義元胞集合S：S={0，1，2，…，k-1}，其中元胞鄰居半徑為r，則在t時刻，位置(i，j)的狀態記為，見圖1。

圖1 元胞位置示意圖

對于Neumann鄰居，鄰居關系定義為

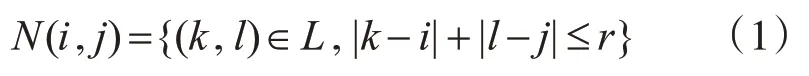
對于Moore鄰居，鄰居關系定義為

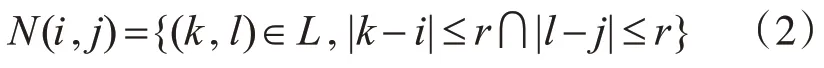
定義cit為t 時刻位于i 處的元胞，局部演化規則函數f和全局演化規則F，之間關系如下：

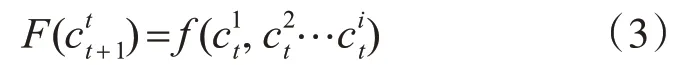
全局演化規則是所有局部演化規則的集合，元胞每一次演化都對周圍元胞產生影響，促使所有元胞同步更新位置和狀態，模擬疏散人員復雜行為過程。

3 粒子群模型

粒子群PSO 算法是基于鳥類群體覓食行為的演化算法。搜索空間中的每只鳥對應全局的每個解，每個粒子根據鄰居粒子尋找的最優信息改變自身位置和飛行狀態，迭代找到全局最優解。目前粒子群算法已廣泛應用與求解離散優化問題，實現步驟如下：

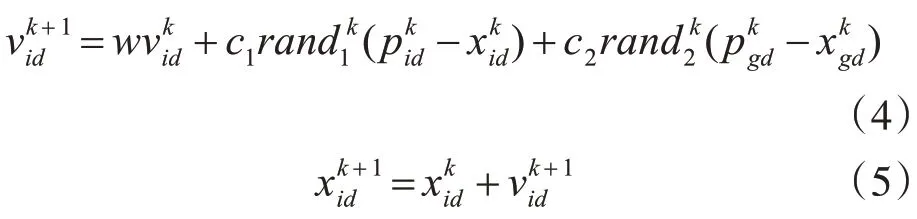
在n個粒子群組成的d維密閉搜索空間，第i個粒子位置為xi=(xi1，xi2，…，xid)，速率為vi=(vi1，vi2，…，vid)t。每個粒子以尋找鄰居全局最優解為目標更新自身飛行速率和位置狀態：其中，c1和c2是學習因子，k為迭代次數，W 為慣性權重，rand是［0，1］區間平均分布的隨機數，表示粒子在第d 維空間速率，是第i 個粒子經k 次迭代后的極值，是粒子群全局極值，和分別是粒子i經k次迭代后的第d維位置和速率。

每個粒子通過搜索鄰居最優解更新自身位置和速率，迭代找到全局最優解，完成搜索過程。

4 新算法實現方法

4.1 基于粒子群優化的元胞更新規則

在元胞自動機模型中，元胞狀態更新策略由元胞自身位置和鄰居元胞狀態共同決定，這與粒子群鳥類尋優思想一致。文章將元胞狀態更新轉變為策略優化問題，通過粒子群算法求解元胞遷移概率最優化形成適應值函數fitness，形成元胞最優演化規則，從而提高疏散效率，減少人員傷亡的目的，算法流程如下：

1）初始化元胞空間大小為M*M 網格，元胞粒子個數為N，速率為

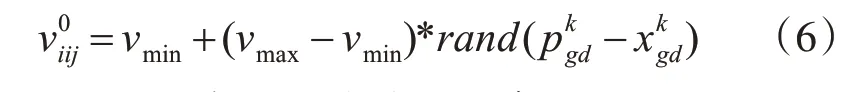
其中vmin和vmax表示元胞粒子速率的上下限。

2）計算元胞粒子適應度值fitness(Pi)，計算第i個粒子極值為

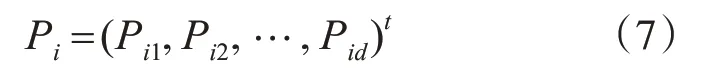
粒子群全局極值為

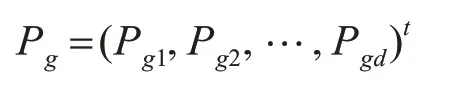
3）利用粒子群更新元胞當前狀態

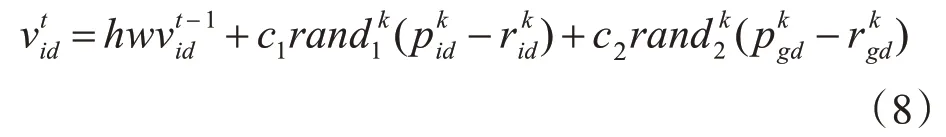
其中，h滿足關系如下：

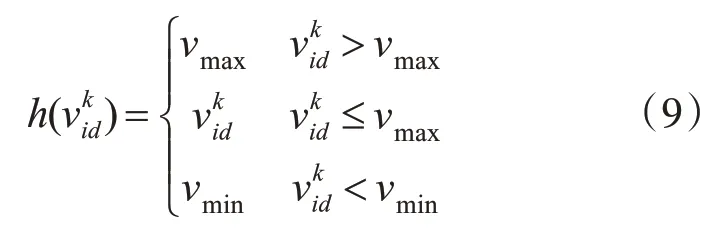
4）更新元胞離子極值

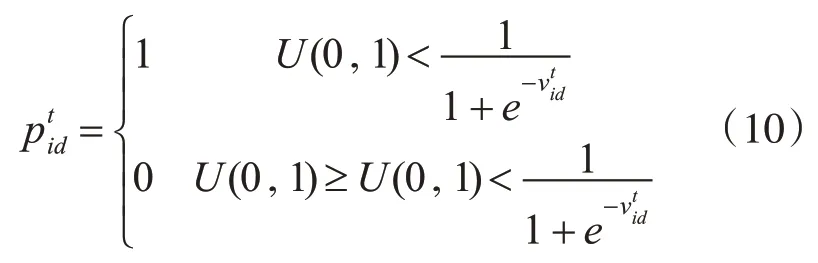
6）計算全局最優演變規則fitness(gb)=max

4.2 元胞自動機模型設計

將元胞自動機空間網格劃分為分成0.3m×03m網格，大小為擁擠時人所占據的平均空間。在t時刻，dv(t)用來表示行人與出口v之間距離，則有：

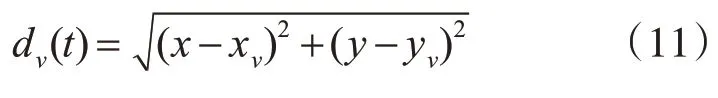
其中，(x，y)表示t時刻行人位置，(xv，yv)表示出口的位置。

定義densityv(t)為出口v的人員密度，則有：

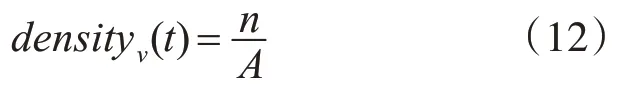
其中，n表示出口區域Sv行人總數。A 為Sv區域內元胞個數。

4.3 粒子群優化元胞遷移概率

若考慮行人與出口之間距離d對元胞遷移的影響，則元胞在t時刻選擇下一網格r遷移的概率為

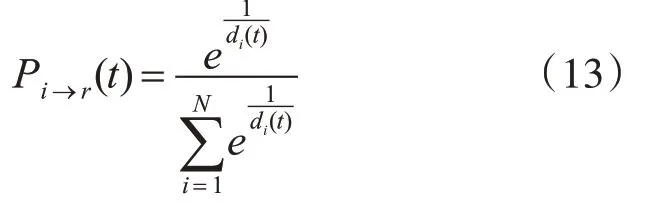
若考慮Sv區域行人密度對元胞遷移的影響，則元胞在t時刻選擇下一網格u遷移的概率為

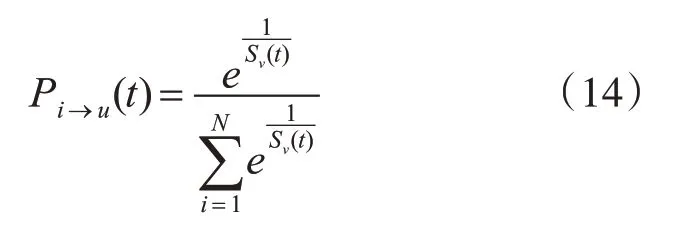
綜合上述兩種因素，元胞遷移概率為

利用粒子群算法計算元胞遷移概率參數α和β的最優組合，形成局部演變規則fitness(pbi)，過程見式（7）～（10）。

4.4 疏散路徑成本計算

為提高疏散效率，應使疏散時間Tmin最小。設（xi，y）i為疏散人員i初始坐標，最優逃生路徑長度為

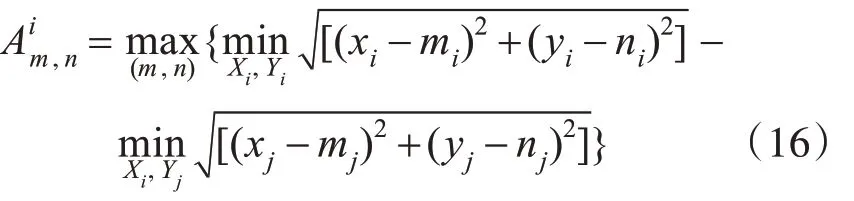
5 仿真測試

5.1 測試環境

仿真實驗選取某市火車站站廳，共7 大出入口，其中，出入口⑦是站廳進門，其余出入口是換乘出口，★代表突發事件地點，見圖2。初始化元胞空間5000*2500 網格，每個網格空間為0.3m×03m，疏散人群1000 人，采用隨機分布方式。粒子群慣性權重Wmax=0.9，Wmin=0.3，算法在各個出口疏散效率見圖3。

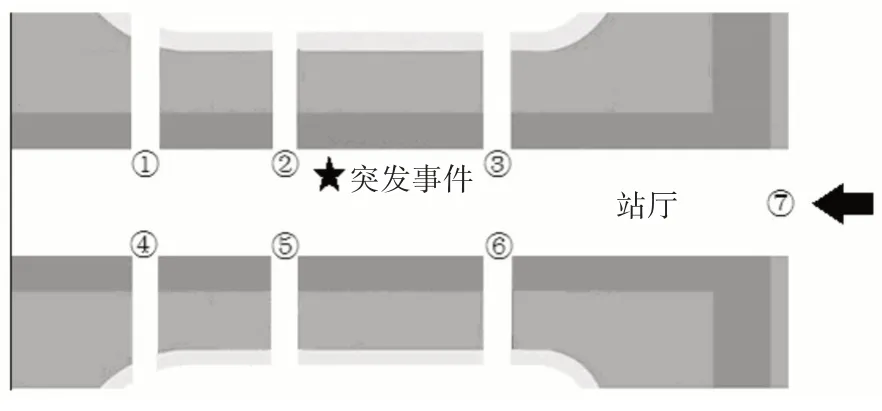
圖2 仿真實驗拓撲圖

5.2 測試結果

從圖3 可以看出，各個出口疏散效率有較大差異，其中出口⑦疏散效率最高，在相同時間疏散近1/4 人群，究其原因，首先，出口⑦所占網格空間較大，經粒子群求解最優適應度函數致使其通向出口⑦的元胞遷移概率較高；其次，受行人對陌生環境和趨眾心理影響，習慣按進門方向折路返回。而出口②疏散效率最低，因為其距離突發事件較近，行人受趨利避害效應逃亡其他出口，這與實際情況相符。

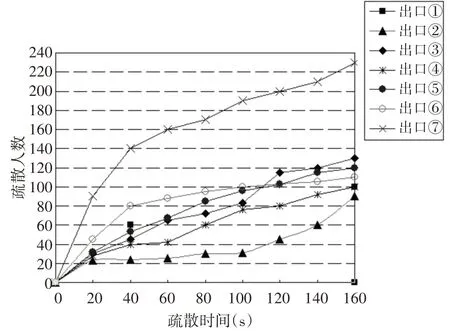
圖3 各出口疏散效率對比圖

6 結語

文章將元胞狀態更新轉變為策略優化問題，通過粒子群算法求解元胞遷移概率最優化適應值函數，形成元胞最優演化規則，從而提高疏散效率，減少人員傷亡，對密集人群場所疏散演練和檢驗建筑設計合理性等具有重要現實意義。