改進(jìn)型極限學(xué)習(xí)機(jī)模型在糧食產(chǎn)量預(yù)測(cè)中的應(yīng)用?

吳耀東

（新疆工程學(xué)院 烏魯木齊 830091）

1 引言

農(nóng)業(yè)是國(guó)民經(jīng)濟(jì)發(fā)展的基石，而糧食則是社會(huì)進(jìn)步與發(fā)展的最基本保障，準(zhǔn)確地預(yù)測(cè)未來(lái)一段時(shí)間的糧食產(chǎn)量，能夠?yàn)檎烙?jì)未來(lái)糧食安全狀況進(jìn)而制定有效政策，實(shí)現(xiàn)糧食安全具有重要意義［1～4］。目前較為常用的糧食產(chǎn)量預(yù)測(cè)方法包括遙感預(yù)測(cè)法［5］、時(shí)間序列預(yù)測(cè)法［1］、灰色模型法、BP 神經(jīng)網(wǎng)絡(luò)［2］和支持向量機(jī)（SVM）［6］等。文獻(xiàn)［1］和［2］分別利用ARIMA 和BP 神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)糧食產(chǎn)量。文獻(xiàn)［6］利用遺傳算法優(yōu)化SVM 模型參數(shù)，應(yīng)用于糧食產(chǎn)量預(yù)測(cè)。

上述的糧食產(chǎn)量預(yù)測(cè)方法存在一些不足，比如BP 神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)速度較慢，并且可能陷入局部最優(yōu)，影響分類精度；SVM 對(duì)大規(guī)模訓(xùn)練樣本的建模存在計(jì)算量大的問(wèn)題等。極限學(xué)習(xí)機(jī)（ELM）作為一種新型的單隱層前饋神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法［7］，具有學(xué)習(xí)速度快、泛化能力強(qiáng)等優(yōu)點(diǎn)［8～9］，已經(jīng)在時(shí)間序列預(yù)測(cè)［10］、模式識(shí)別［11～14］等領(lǐng)域得到了應(yīng)用。

對(duì)于ELM，隱節(jié)點(diǎn)數(shù)目L 對(duì)模型預(yù)測(cè)準(zhǔn)確性影響較大，較小的L會(huì)降低ELM預(yù)測(cè)準(zhǔn)確性，較大的L會(huì)降低ELM 的泛化性能［15］。為了確定合適的隱節(jié)點(diǎn)數(shù)目，需要計(jì)算不同L 下ELM 的預(yù)測(cè)誤差，但每次計(jì)算不同L 對(duì)應(yīng)的輸出權(quán)重時(shí)，需要重復(fù)計(jì)算隱層矩陣的廣義逆矩陣，當(dāng)L 較大時(shí)，會(huì)增大計(jì)算量。為此，推導(dǎo)L 遞增情況下輸出權(quán)重的遞推公式，提出增長(zhǎng)ELM（GELM）算法，從而有效降低ELM的計(jì)算量，實(shí)驗(yàn)結(jié)果證明了本文提出方法的有效性。

2 增長(zhǎng)極限學(xué)習(xí)機(jī)（GELM）

GELM 的思路是從最小的隱節(jié)點(diǎn)數(shù)目L 開(kāi)始，按固定數(shù)量逐漸增加ELM 中的L，直到滿足規(guī)定的停止準(zhǔn)則，最終確定ELM 中的L。同時(shí)，每次增加L時(shí)均需重新計(jì)算輸出權(quán)重β，當(dāng)L 較大時(shí)，Η的Moore-Penrose 廣義逆矩陣Η?的計(jì)算量迅速增加，為此，推導(dǎo)ELM 中L 遞增情況下β的遞推計(jì)算公式，降低ELM的計(jì)算量。

2.1 輸出權(quán)重遞推計(jì)算

假設(shè)ELM 隱節(jié)點(diǎn)數(shù)目為L(zhǎng) 時(shí)的隱層矩陣為HL，如式（1）所示。當(dāng)隱節(jié)點(diǎn)數(shù)目增加ΔL 時(shí)，ELM的隱層矩陣變?yōu)閉， 其中 ΔHΔL為新增加的ΔL 個(gè)隱節(jié)點(diǎn)組成的隱層矩陣，如式（2）所示。

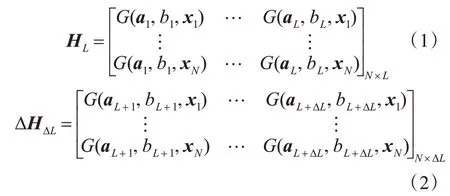
式中，ai∈?n和bi∈? 表示隱含層參數(shù)。對(duì)于包含ΔL+L個(gè)隱節(jié)點(diǎn)的ELM，輸出權(quán)重為

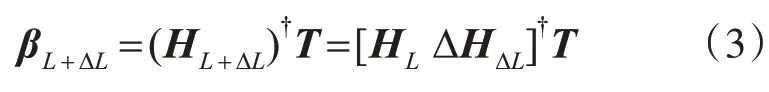
由式（3）可知，計(jì)算βL+ΔL時(shí)，需要計(jì)算N×（L+ΔL）維矩陣的廣義逆矩陣其中N 為樣本數(shù)量。當(dāng)L+ΔL 較大時(shí)的計(jì)算量迅速增加。

為此，推導(dǎo)隱節(jié)點(diǎn)數(shù)目按ΔL 遞增情況下，[HLΔHΔL]?的遞推計(jì)算公式，可以有效降低計(jì)算量。推導(dǎo)過(guò)程如下。

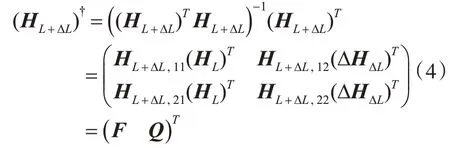
式中

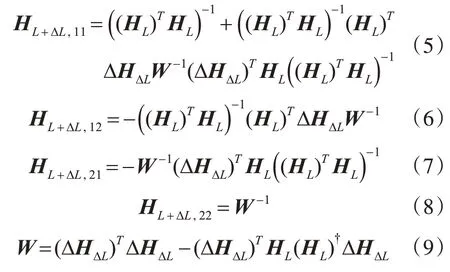
根據(jù)式（4）和式（7）～（9），令σ=I-HL(HL)?，可知σΤ=σ，σ2=σ，則

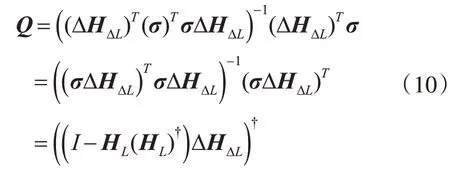
同理，根據(jù)式（4）～（6）和式（10），可以計(jì)算F為

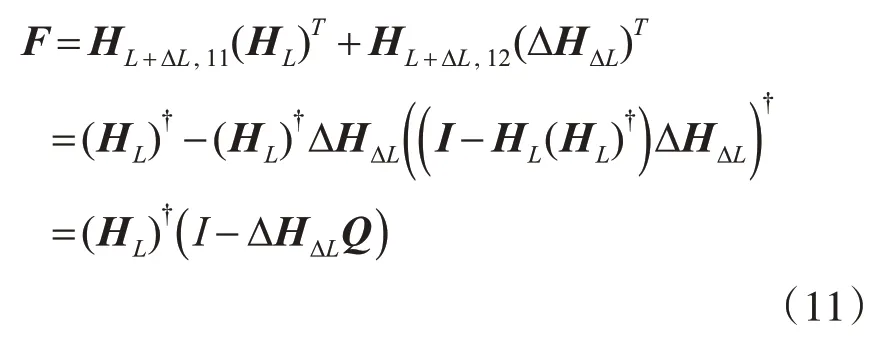
則式（3）的計(jì)算可以變?yōu)?/p>

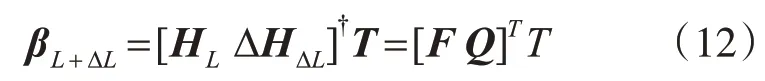
2.2 GELM算法流程

步驟1初始化GELM 的模型參數(shù)，其中初始隱節(jié)點(diǎn)數(shù)目為L(zhǎng)0，生成由L0個(gè)隱節(jié)點(diǎn)組成的H0矩陣，如式（1）所示，其中參數(shù)ai和bi利用隨機(jī)生成方式獲得。設(shè)定單次增加的隱節(jié)點(diǎn)數(shù)目為ΔL，并令隱節(jié)點(diǎn)遞增次數(shù)k=0。計(jì)算初始的輸出權(quán)重矩陣β0：

步驟2令k=k+1，第k 次增加的隱節(jié)點(diǎn)ΔL 對(duì)應(yīng)的隱層矩陣ΔHΔL如式（8）所示。根據(jù)式（13）得

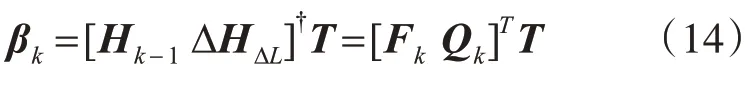
步驟3令Hk=［Hk-1ΔHΔL］，Lk=Lk-1+ΔL。計(jì)算預(yù)測(cè)誤差

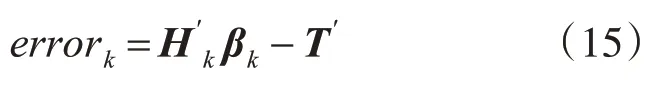
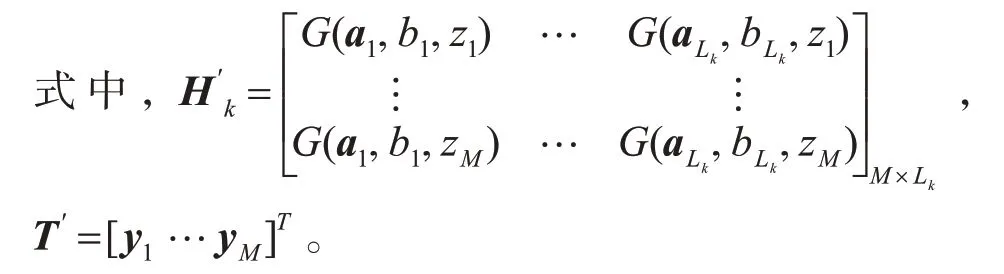
步驟4若errork＜errork-1，轉(zhuǎn)入步驟2；若errork≥errork-1，轉(zhuǎn)入步驟5。

步驟5確定GELM 的隱節(jié)點(diǎn)數(shù)目為L(zhǎng)k，其對(duì)應(yīng)的輸出權(quán)重為βk。

3 糧食產(chǎn)量預(yù)測(cè)流程

基于GELM的糧食產(chǎn)量預(yù)測(cè)算法整理如下。

步驟1將已知的糧食產(chǎn)量轉(zhuǎn)換成訓(xùn)練樣本和參數(shù)優(yōu)化樣本，其中為第i年度的糧食產(chǎn)量，τ為嵌入維數(shù)。的數(shù)據(jù)形式與相同。

步驟2根據(jù)3.2 節(jié)的GELM 算法流程，利用和{建立GELM預(yù)測(cè)模型。

步驟3為預(yù)測(cè)第n+1 年度糧食產(chǎn)量，將第n-τ+1 年度至第n 年度糧食產(chǎn)量作為輸入向量，計(jì)算對(duì)應(yīng)，計(jì)算xn對(duì)應(yīng)輸出，即為第n+1年度預(yù)測(cè)值。

4 實(shí)例驗(yàn)證

4.1 實(shí)驗(yàn)數(shù)據(jù)

選取全國(guó)1960-2015 年的糧食總產(chǎn)量作為實(shí)驗(yàn)數(shù)據(jù)，見(jiàn)表1。由表1 可以看出，1960-2015 年糧食產(chǎn)量總體呈增長(zhǎng)趨勢(shì)。1960-1977 年期間，糧食總產(chǎn)量增長(zhǎng)較為緩慢；1978-1999 年期間，糧食產(chǎn)量增長(zhǎng)速度較快；在2000 年，糧食產(chǎn)量較前一年出現(xiàn)下降，直到2004 年，糧食產(chǎn)量恢復(fù)增長(zhǎng)趨勢(shì)。選取1960-1994 年的產(chǎn)量作為訓(xùn)練樣本，1995-2004年的產(chǎn)量作為參數(shù)優(yōu)化樣本，優(yōu)化糧食產(chǎn)量預(yù)測(cè)模型參數(shù)，利用2005-2015 年的產(chǎn)量作為測(cè)試樣本，檢驗(yàn)預(yù)測(cè)模型的預(yù)測(cè)性能。訓(xùn)練樣本、參數(shù)優(yōu)化樣本和測(cè)試樣本轉(zhuǎn)化成形 式 ，其 中為第i 年的糧食產(chǎn)量，τ為時(shí)間序列嵌入維數(shù)。

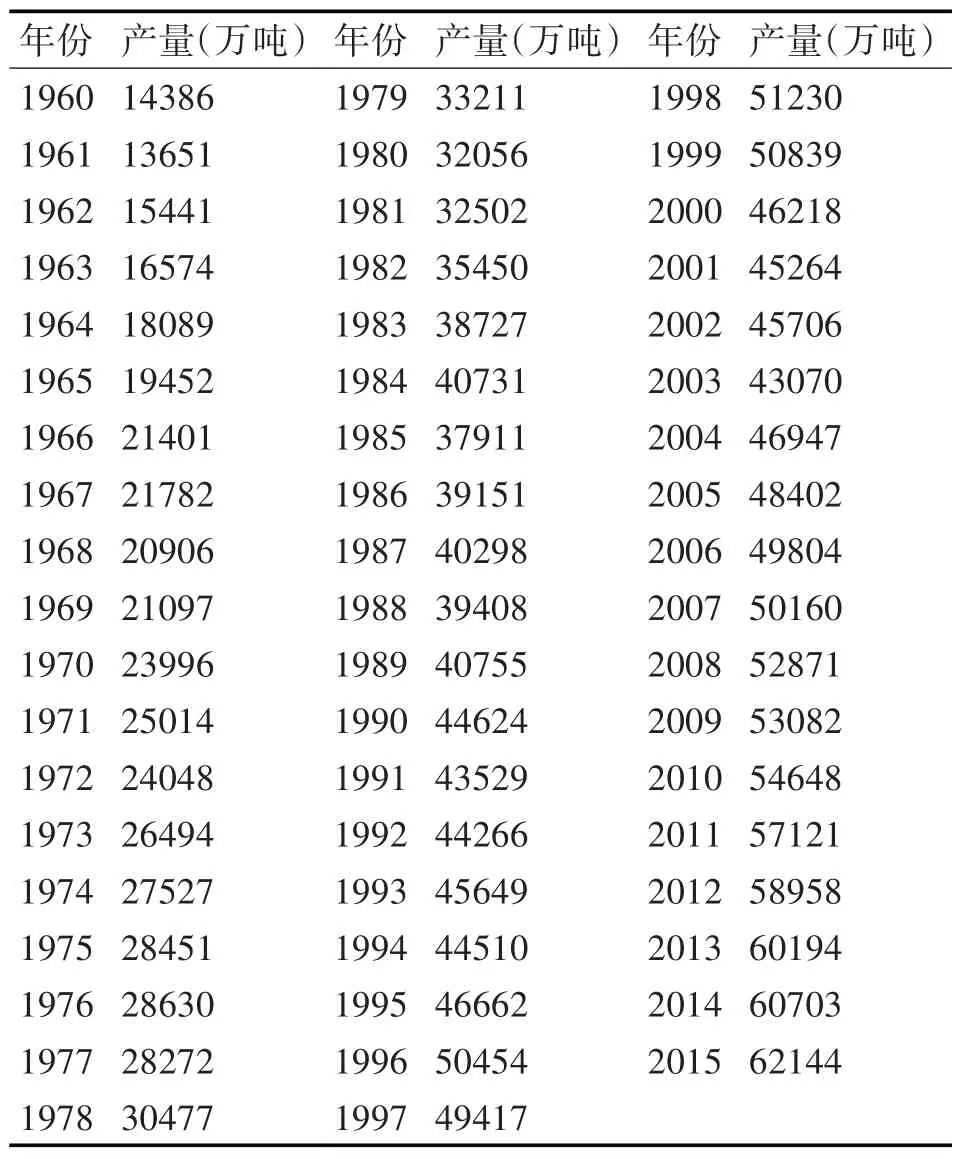
表1 全國(guó)1960-2015年的糧食產(chǎn)量

4.2 參數(shù)選擇

設(shè)定GELM 初始隱節(jié)點(diǎn)數(shù)目L0=50，單次隱節(jié)點(diǎn)遞增個(gè)數(shù)ΔL=20。將GELM 用于時(shí)間序列預(yù)測(cè)時(shí)，嵌入維數(shù)τ影響著預(yù)測(cè)準(zhǔn)確性。分別令τ=2，3，…，10。對(duì)于每個(gè)選定的τ，計(jì)算GELM 對(duì)應(yīng)的參數(shù)優(yōu)化樣本預(yù)測(cè)誤差絕對(duì)值，選取誤差最小值作為每個(gè)τ對(duì)應(yīng)的預(yù)測(cè)誤差。則不同τ值對(duì)應(yīng)的預(yù)測(cè)誤差如圖1 所示。可以看出，τ=3 時(shí)預(yù)測(cè)誤差最小。圖2 所示為τ=3 時(shí)，GELM 從初始隱節(jié)點(diǎn)L0開(kāi)始，逐步按ΔL 遞增隱節(jié)點(diǎn)數(shù)目，其對(duì)應(yīng)的參數(shù)優(yōu)化樣本預(yù)測(cè)誤差。確定GELM的隱節(jié)點(diǎn)數(shù)目為210。

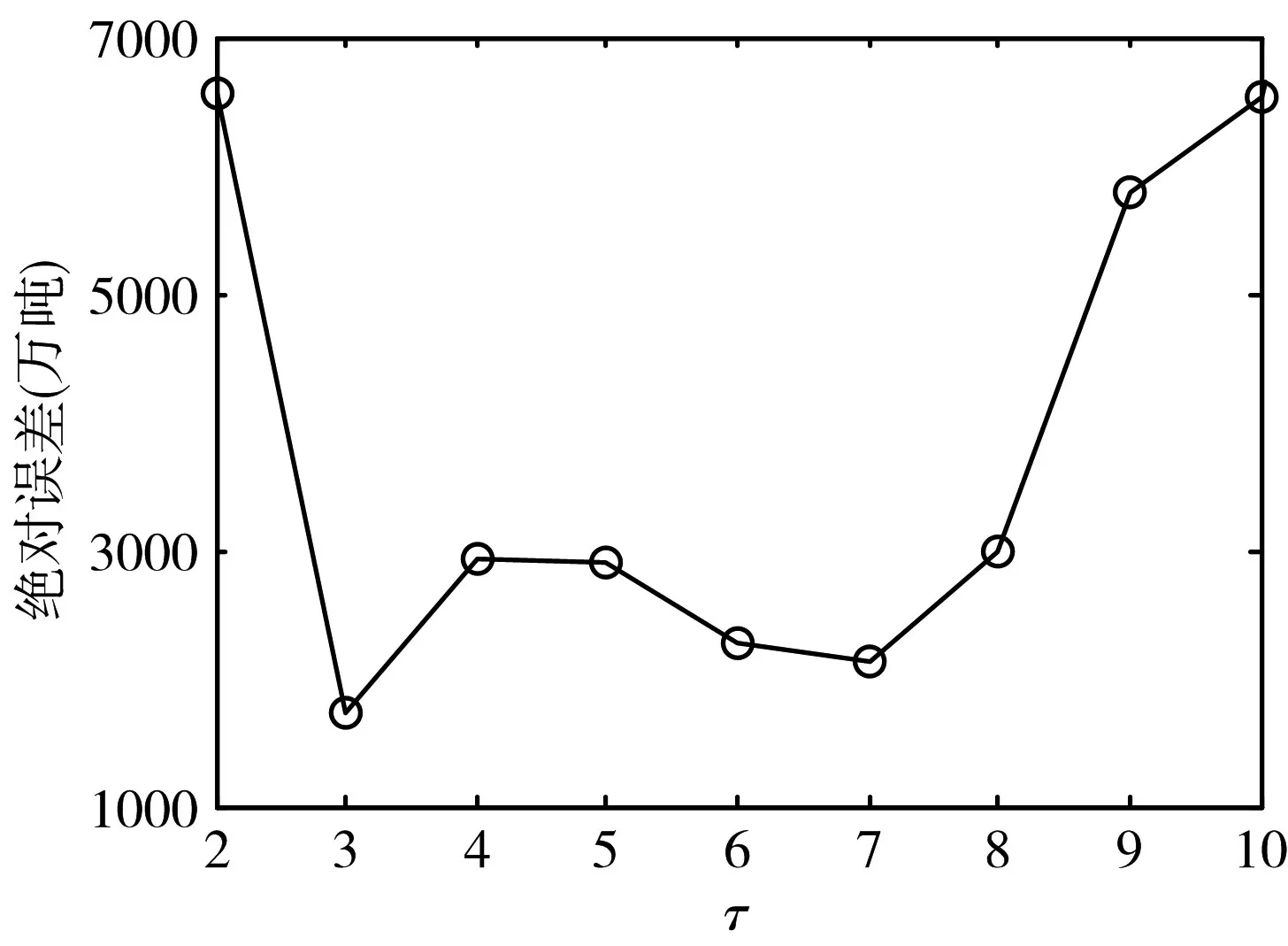
圖1 GELM不同τ值對(duì)應(yīng)的預(yù)測(cè)誤差

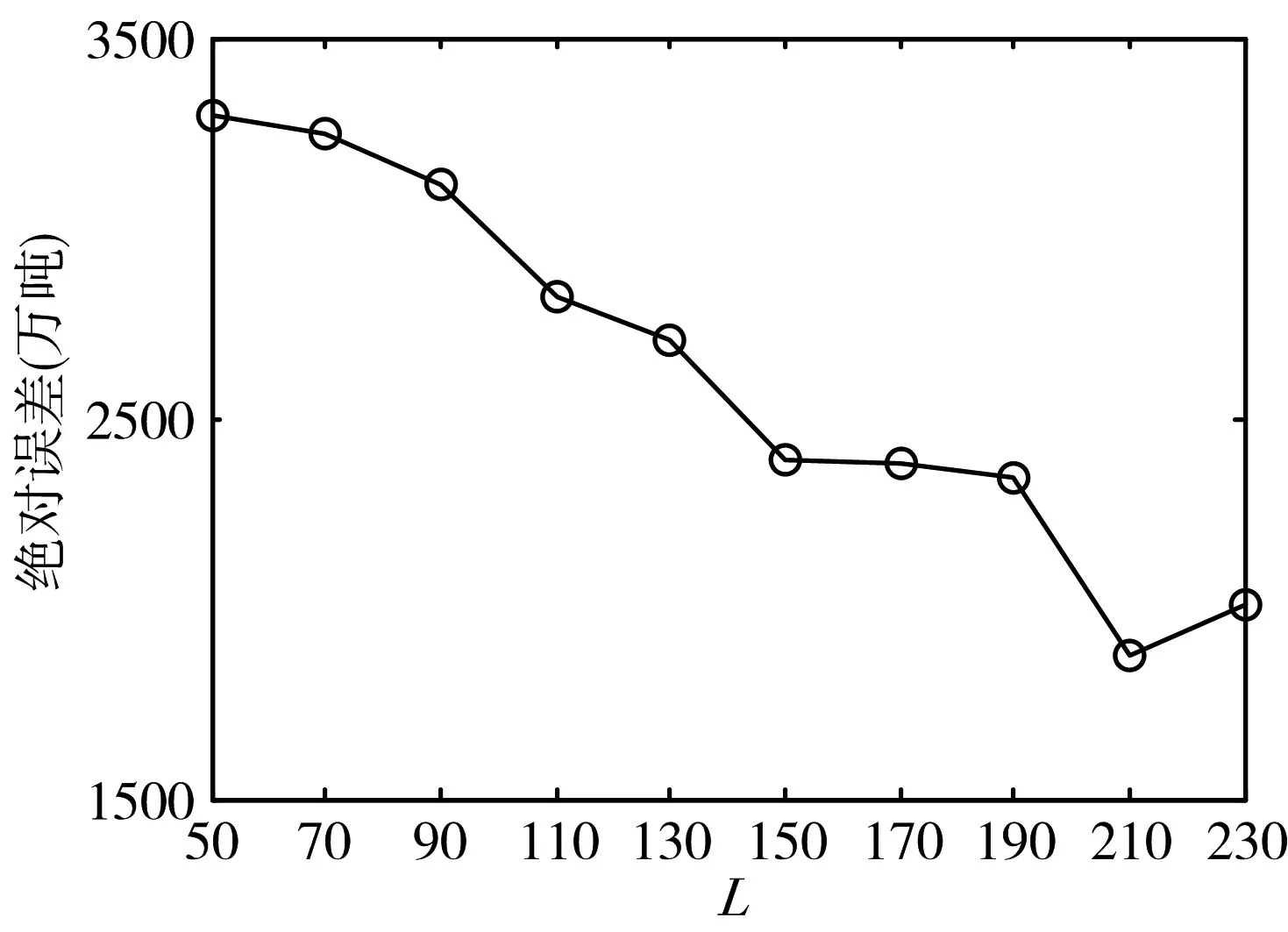
圖2 GELM隨隱節(jié)點(diǎn)數(shù)目遞增對(duì)應(yīng)的參數(shù)優(yōu)化樣本預(yù)測(cè)誤差

分別采用標(biāo)準(zhǔn)的ELM 和支持向量機(jī)（SVM）作為對(duì)比方法，其中SVM選用libsvm工具箱中提供的函數(shù)。對(duì)于ELM 和SVM，時(shí)間序列的嵌入維數(shù)τ同樣需要人為確定。此外，影響ELM 的參數(shù)為隱節(jié)點(diǎn)數(shù)目L，影響SVM 的參數(shù)為C 和γ。分別令ELM中的L={50，70，…，300}，SVM 中的C 和γ={2-14，2-13，…，214，215}，采用與GELM 同樣的參數(shù)尋優(yōu)方法，得到ELM 和SVM 的最優(yōu)參數(shù)如表2 所示。實(shí)驗(yàn)所用計(jì)算機(jī)為Windows XP 系統(tǒng)，Intel i5 CPU（主頻3.5GHz），4GB內(nèi)存，仿真軟件為Matlab R2011b。

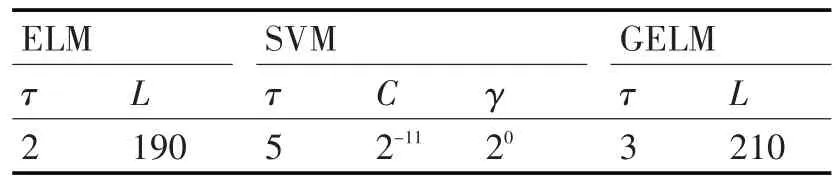
表2 不同方法最優(yōu)參數(shù)

4.3 預(yù)測(cè)結(jié)果

三種方法按照表2 的參數(shù)建立預(yù)測(cè)模型，進(jìn)行50 次蒙特卡洛仿真，計(jì)算得到訓(xùn)練樣本的平均絕對(duì)誤差（MAE）如表3 所示。可以看出，相比于SVM，GELM 和ELM 對(duì)訓(xùn)練樣本的預(yù)測(cè)準(zhǔn)確性較高，說(shuō)明GELM和ELM對(duì)于已知數(shù)據(jù)的擬合精度較高。三種方法對(duì)測(cè)試樣本的預(yù)測(cè)結(jié)果和預(yù)測(cè)絕對(duì)誤差分別如圖3 和圖4 所示。進(jìn)行50 次蒙特卡洛仿真，得到三種方法對(duì)測(cè)試樣本的MAE 如表3 所示。對(duì)于測(cè)試樣本而言，GELM 的預(yù)測(cè)準(zhǔn)確性較訓(xùn)練樣本偏低，這主要是因?yàn)闇y(cè)試樣本并沒(méi)有參與預(yù)測(cè)模型的建立過(guò)程，但是GELM 的預(yù)測(cè)結(jié)果的總體趨勢(shì)與實(shí)際情況相符，說(shuō)明GELM 在糧食產(chǎn)量預(yù)測(cè)中的有效性。ELM 和GELM 方法的預(yù)測(cè)誤差較接近，相比之下，GELM 的預(yù)測(cè)精度略高于ELM，SVM預(yù)測(cè)誤差最大。

三種方法的耗時(shí)同樣如表3 所示，其中耗時(shí)包括參數(shù)優(yōu)化樣本尋優(yōu)時(shí)間、訓(xùn)練樣本建模時(shí)間和測(cè)試樣本測(cè)試時(shí)間。可以看出，由于SVM 需要同時(shí)優(yōu)化τ、C和γ三個(gè)參數(shù)，其耗時(shí)最長(zhǎng)。ELM和GELM需要更新τ和L 兩個(gè)參數(shù)，對(duì)于不同的隱節(jié)點(diǎn)數(shù)目L，GELM能夠利用上一步L對(duì)應(yīng)的隱層矩陣的廣義逆矩陣，根據(jù)式（19）的遞推方式計(jì)算當(dāng)前L 對(duì)應(yīng)的隱層矩陣的廣義逆矩陣，繼而更新輸出權(quán)重，而ELM 對(duì)每個(gè)L 均需要重新計(jì)算隱層矩陣的廣義逆矩陣，因此ELM的耗時(shí)高于GELM。

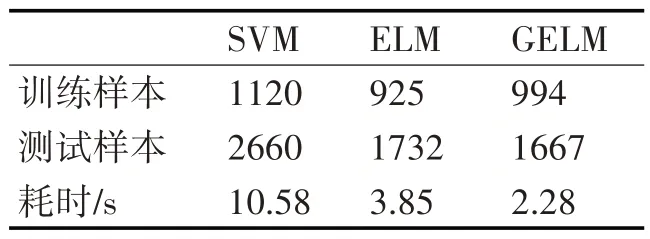
表3 三種方法的MAE誤差和耗時(shí)

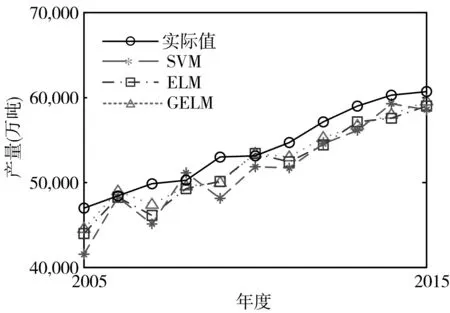
圖3 三種方法對(duì)測(cè)試樣本的預(yù)測(cè)結(jié)果

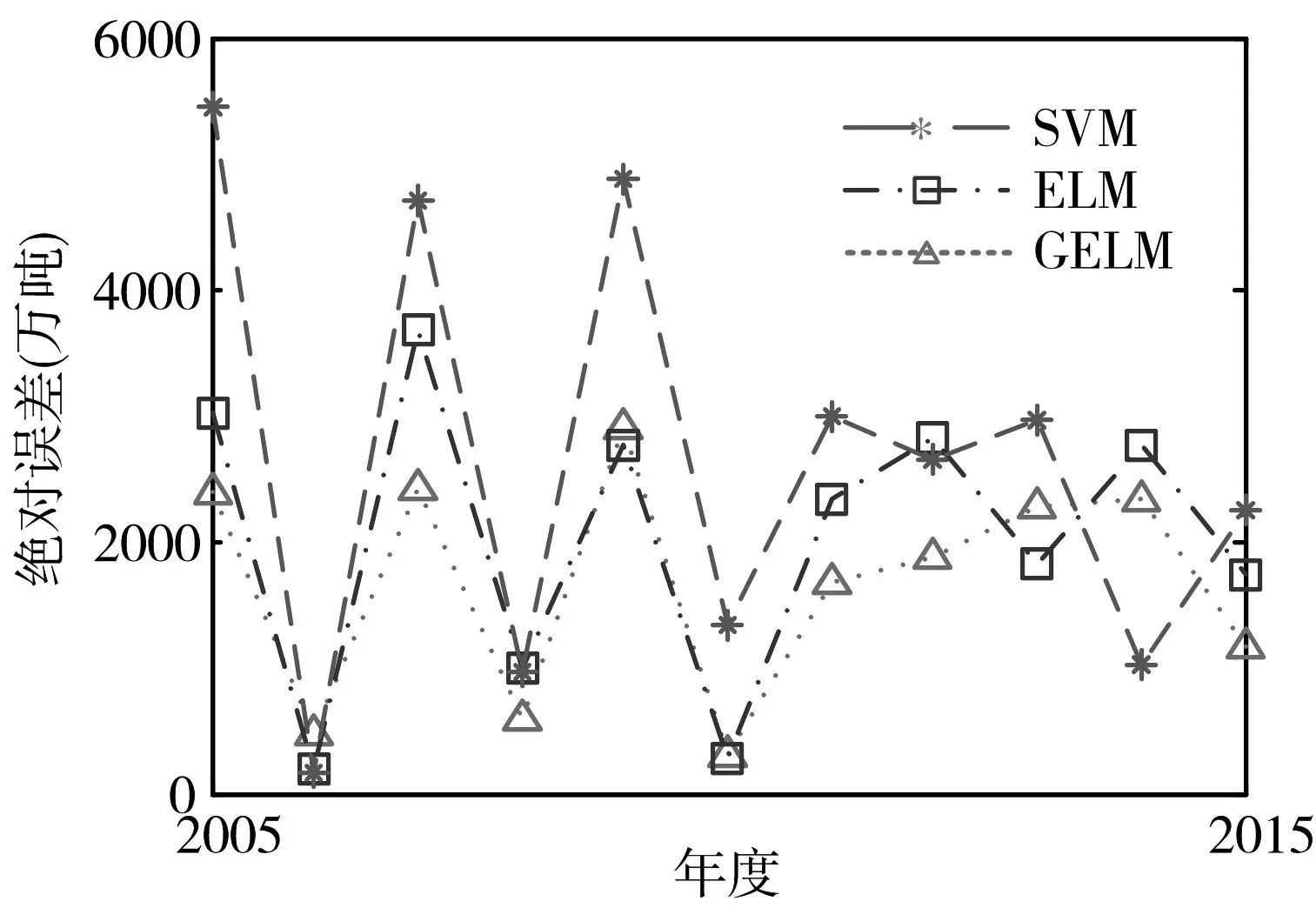
圖4 三種方法對(duì)測(cè)試樣本的預(yù)測(cè)誤差

5 結(jié)語(yǔ)

本文提出了基于GELM 的糧食產(chǎn)量預(yù)測(cè)方法。為了解決ELM 隱層結(jié)構(gòu)優(yōu)化問(wèn)題，推導(dǎo)ELM中隱節(jié)點(diǎn)數(shù)目L 遞增情況下輸出權(quán)重的遞推計(jì)算公式，從而有效降低ELM 的計(jì)算量。糧食產(chǎn)量預(yù)測(cè)結(jié)果表明，GELM 的預(yù)測(cè)精度和耗時(shí)均優(yōu)于SVM，GELM 的預(yù)測(cè)精度與ELM 相似，但耗時(shí)低于ELM，從而證明本文推導(dǎo)的遞推公式可以降低輸出矩陣的計(jì)算量。實(shí)驗(yàn)結(jié)果說(shuō)明本文提出方法可以有效地應(yīng)用于糧食產(chǎn)量預(yù)測(cè)。