考慮不完全維修的裝備單元維修與更換策略優(yōu)化
陳陽隆, 馬彥恒, 侯建強
(陸軍工程大學石家莊校區(qū)無人機工程系, 河北 石家莊 050003)
傳統(tǒng)的預防性維修主要是指定期維修,它存在維修不足或維修過剩的問題[1]。隨著現(xiàn)代科學理論與技術的發(fā)展,視情維修逐漸發(fā)展成為預防性維修的主要方式。基于認知測試性設計[2]的裝備可以實時的評估自身狀態(tài)。當裝備狀態(tài)不滿足任務要求時,可視情制定維修策略,安排相應的維修措施,使裝備及時、準確地消除潛在隱患,提高運行的可靠性,降低突發(fā)故障帶來的經(jīng)濟損失及安全問題。
在視情維修決策建模中,維修效果是對失效單元修后性能恢復程度的衡量。維修效果主要包括完全維修(修復如新)、不完全維修和最小維修(修復如舊),其中基于完全維修和最小維修的建模理論相對較為完善[3]。由于不完全維修介于完全維修和最小維修之間,其更加貼合工程實際,已成為當前維修建模研究的熱點問題[4]。如:WU等[5]介紹了現(xiàn)有不完全維修模型中存在的共性問題,并依據(jù)維修后系統(tǒng)的退化方式,將不完全維修模型分為線性與非線性2大類;程志君等[6]采用馬爾科夫鏈建立了系統(tǒng)退化維修模型,通過狀態(tài)轉(zhuǎn)移率表征不完全維修;潘剛等[7]采用Semi-Markov模型描述裝備單元的性能衰退過程,提出了預防性維修和修復性維修相結(jié)合的不完全維修決策方法;LIU等[8]將裝備單元的狀態(tài)轉(zhuǎn)移率與維修次數(shù)相關聯(lián),采用準更新過程理論描述裝備單元的壽命變化情況,建立了基于非齊次連續(xù)時間的馬爾可夫視情維修決策模型。
綜上所述可以看出:當前研究僅考慮了維修次數(shù)對維修效果的影響,且建立的不完全維修模型雖然表達了維修效果中的修復非新思想,但并未考慮維修后裝備單元衰退速度的變化。筆者首先將維修費用和維修次數(shù)引入不完全維修模型,并假設各裝備單元維修后均處于最高性能狀態(tài)(并非修復如新);其次,采用性能狀態(tài)衰退速度來描述不完全維修的維修效果,采用齊次馬爾科夫模型來表征裝備單元的衰退規(guī)律;最后,結(jié)合準更新過程建立不完全維修模型,并針對不同裝備系統(tǒng)的任務性能需求,尋找最優(yōu)的裝備單元維修費用和更換策略,實現(xiàn)裝備系統(tǒng)單位時間的凈效益最大化。
1 模型假設與描述
1.1 模型假設
1) 裝備系統(tǒng)L由M個裝備單元s構(gòu)成,其中連接方式可以是任意的,如串并聯(lián)結(jié)構(gòu)。
2) 裝備單元s(s=1,2,…,M)有ks個不同的狀態(tài)。其中:g(s,i)為裝備單元s處于狀態(tài)i(i=1,2,…,ks)時的性能水平,表征裝備單元s對裝備系統(tǒng)正常運行的貢獻度;ps,i(t)為裝備單元s在t時刻處于狀態(tài)i的概率。
3) 裝備單元的狀態(tài)轉(zhuǎn)移過程符合齊次馬爾科夫模型。
4) 裝備單元狀態(tài)監(jiān)測費用忽略不計,當監(jiān)測到裝備單元狀態(tài)低于維修閾值時,即進行預防性維修或更換,且維修為不完全維修,同時預防性維修成本<更換成本。
5) 維修效果與維修費用有關,其函數(shù)關系可通過歷史數(shù)據(jù)得到。
6) 裝備單元每次維修的維修費用是一致的。
7) 優(yōu)化目標為在滿足裝備系統(tǒng)的任務性能需求下,優(yōu)化裝備單元s的維修費用cs和更換策略Ns(即預防性維修次數(shù)),使裝備系統(tǒng)單位時間的凈效益最大。
8) 裝備單元采取維修措施后,裝備恢復到最高性能狀態(tài),但并非修復如新,修復后的裝備單元的性能衰退速度加快,即狀態(tài)轉(zhuǎn)移率會增大。
1.2 模型描述
隨著認知測試性技術的發(fā)展,可以實時監(jiān)測裝備中各裝備單元的狀態(tài)。當裝備單元狀態(tài)低于維修閾值時,可采取維修或更換措施,使其得到不同程度的恢復。當采取維修措施時,修后裝備單元的狀態(tài)為不完全修復狀態(tài),且隨著維修次數(shù)的增加,裝備單元的可靠性將快速下降,進而影響裝備任務的完成。因此,筆者考慮不完全維修,根據(jù)裝備系統(tǒng)的任務性能需求,建立裝備單元維修與更換策略權(quán)衡優(yōu)化模型,為裝備系統(tǒng)中每個單元選擇最優(yōu)的維修費用和更換策略,使裝備系統(tǒng)單位時間的凈效益最大,即
C=Cp-Cq-Ca;
(1)
(2)
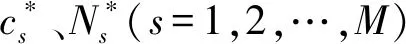
2 模型建立
2.1 基于齊次馬爾科夫模型的裝備單元瞬時狀態(tài)概率模型
采用馬爾科夫模型[9]的離散狀態(tài)來描述裝備單元的性能狀態(tài)。設X(t)∈{1,2,…,k}為裝備單元在任意時刻t的狀態(tài)集合,則根據(jù)馬爾科夫性有
P{X(tn)=xn|X(t1)=x1,X(t2)=x2,…,
X(tn-1)=xn-1}=P{X(tn)=
xn|X(tn-1)=xn-1},
(3)
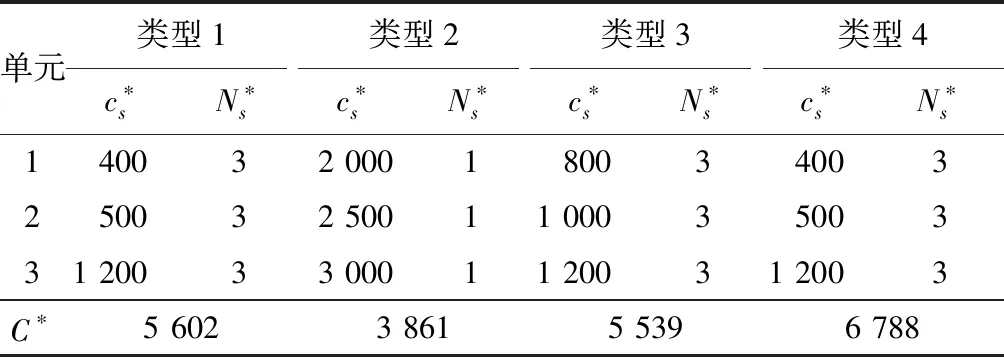
式中:X(tn)=xn,表示在tn時刻裝備單元的狀態(tài)為xn,0≤t1 裝備單元在t(t≥0)時刻的狀態(tài)i(i=1,2,…,k),經(jīng)Δt(Δt≥0)后轉(zhuǎn)移到狀態(tài)j(j=1,2,…,k,j≠i)的狀態(tài)轉(zhuǎn)移概率為 Qi,j(t,t+Δt)=P{X(t+Δt)=j|X(t)=i}= λi,j(t)·Δt+o(Δt),i≠j, (4) 式中:λi,j(t)為裝備單元在t時刻離開狀態(tài)i轉(zhuǎn)移到狀態(tài)j的狀態(tài)轉(zhuǎn)移率;o(Δt)為Δt的高階無窮小。若λi,j(t)為與時間無關的常數(shù),則該過程為齊次馬爾科夫過程;反之,則為非齊次馬爾科夫過程。 由圖1可知:裝備單元s的狀態(tài)轉(zhuǎn)移率矩陣 (5) (6) 設裝備單元最低狀態(tài)為維修閾值狀態(tài),當達到該狀態(tài)時,立即對裝備單元進行維修。修后裝備單元恢復至最高性能狀態(tài),但并非修復如新,在新的運行周期中裝備單元的性能衰退速度將加快。運用準更新過程理論[11-12],將裝備單元第r-1次與第r次維修之間的時間間隔定義為第r次維修周期,采用隨機變量Hr來描述第r次維修周期中裝備單元的壽命,且滿足 H1=Z1,H2=αZ2,…,Hr=αr-1Zr, (7) 式中:Zr為獨立同分布隨機變量;H1,H2,…,Hr,…為一個以α(α>0)為參數(shù)的準更新過程。在不同維修周期中,裝備單元壽命的變化情況為:當0<α<1時,裝備單元壽命隨著維修周期的增加而減小;當α=1時,裝備單元壽命保持不變;當α>1時,裝備單元壽命隨著維修周期的增加而增加。且有 (8) 采用裝備單元的狀態(tài)概率表示可靠度,結(jié)合式(8)與可靠性理論可得[13-14]: (9) (10) (11) (12) 式中: (13) (14) (15) (16) 通用生成函數(shù)作為一種簡潔、高效的離散隨機變量組合運算工具,已被廣泛地運用于裝備系統(tǒng)的狀態(tài)評估和可靠性研究等領域中。裝備是由一系列裝備單元按一定的結(jié)構(gòu)關系構(gòu)成的有機整體,因此可采用通用生成函數(shù)[15]由裝備單元的穩(wěn)態(tài)概率分布計算出裝備系統(tǒng)的穩(wěn)態(tài)概率分布。由式(12)求出的裝備單元s的穩(wěn)態(tài)概率分布的通用生成函數(shù)為 (17) 式中:z沒有具體的取值,主要用于區(qū)分狀態(tài)性能g(s,i)和對應的概率ps,i。則整個裝備的穩(wěn)態(tài)概率分布為 UL(z)=?{u1(z),u2(z),…,uM(z)}= (18) 式中:“?”為通用生成函數(shù)中的求和算子;is(s=1,2,…,M)為裝備單元s的狀態(tài)變量,pL,i為裝備系統(tǒng)L在狀態(tài)i的穩(wěn)態(tài)概率;g(L,i)為裝備系統(tǒng)L在狀態(tài)i時的性能水平;kL為裝備系統(tǒng)最大可能的狀態(tài)數(shù);W(·)為裝備系統(tǒng)的結(jié)構(gòu)函數(shù)。當電流傳輸型系統(tǒng)由2個單元串聯(lián)組成時,有 W(g1,g2)=min{g1,g2}; (19) 若為并聯(lián),則有 W(g1,g2)=g1+g2。 (20) 根據(jù)式(1)裝備系統(tǒng)單位時間的凈效益和裝備系統(tǒng)單位時間的性能水平的期望值,可得裝備系統(tǒng)單位時間的性能水平回報 (21) 式中:ce為裝備系統(tǒng)在單位時間內(nèi)單位性能水平下的回報量。 在策略Ns下,裝備單元s的單位時間維修費用 (22) 則整個裝備系統(tǒng)單位時間的維修費用 (23) 設裝備系統(tǒng)的最低任務性能需求水平為w,當裝備系統(tǒng)性能水平低于w時,需要進行補償,則裝備系統(tǒng)性能水平不滿足任務需求水平w時,帶來的性能補償 (24) 式中:cf為裝備系統(tǒng)在單位時間內(nèi)單位性能水平不足時的補償量。 為使裝備系統(tǒng)單位時間的凈效益C最大,需要優(yōu)化為裝備單元s安排的維修費用cs與更換策略Ns,權(quán)衡優(yōu)化模型如式(2)所示。 為了解決求解空間維數(shù)爆炸問題,將裝備單元s的維修分為v(v=1,2,…,ns)個等級,則第v個維修等級對應的維修費用 (25) 以某無人機控制裝備為例,其由3個裝備單元構(gòu)成,如圖2所示。其中:單元1、2有3個不同的性能水平,單元3有4個不同的性能水平。性能水平代表處于該狀態(tài)的裝備單元對裝備正常運行的貢獻度,一般狀態(tài)i越低,其對應的性能水平g(s,i)也將越小,一般結(jié)合裝備歷史數(shù)據(jù)通過分析裝備性能得到。裝備單元的性能水平與狀態(tài)轉(zhuǎn)移的率相關數(shù)據(jù)如表1所示。 單元性能水平/%狀態(tài)轉(zhuǎn)移率/(次·月-1)1g(1,3)=30λ13,2=0.30,λ13,1=0.40g(1,2)=20λ12,1=0.50g(1,1)=0 —2g(2,3)=45λ23,2=0.30,λ23,2=0.35g(2,2)=30λ22,1=0.45g(2,1)=0 —3g(3,4)=90λ34,3=0.30,λ34,2=0.35,λ34,1=0.40g(3,3)=70λ33,2=0.50,λ33,1=0.65g(3,2)=40λ32,1=0.85g(3,1)=0 — 根據(jù)各裝備單元的狀態(tài)轉(zhuǎn)移率,通過求解Kolmogorov微分方程組可得到各裝備單元的瞬時狀態(tài)概率分布分別為 P1(t)=(p1,1(t),p1,2(t),p1,3(t))= P2(t)=(p2,1(t),p2,2(t),p2,3(t))= P3(t)=(p3,1(t),p3,2(t),p3,3(t),p3,4(t))= (1-2e-1.15t+5.25e-1.05t-4.25e-0.85t, 5e-1.15t-9.25e-1.05t+4.25e-0.85t, 3(e-1.05t-e-1.15t),e-1.05t)。 各裝備單元的相關維修參數(shù)如表2所示。其中 表2 裝備單元s的維修決策參數(shù) 費用單位為元。 在裝備單元更換策略下,可得到裝備系統(tǒng)的穩(wěn)態(tài)概率。根據(jù)式(18)可計算出裝備系統(tǒng)的狀態(tài)性能水平及其對應的概率。設ce=2,cf=0.8,w=60%,應用遺傳算法可得到裝備系統(tǒng)的優(yōu)化結(jié)果,如表3所示。 表3 某無人機控制裝備維修決策優(yōu)化結(jié)果 由表3可以看出: 1) 類型1的維修策略為:每次失效后安排的維修費用為400元,并在第3次失效后安排更換,其裝備系統(tǒng)的最大單位時間凈效益為5 602元; 2) 類型2為傳統(tǒng)的完全維修,即每次失效后采取更換措施,其裝備系統(tǒng)最大單位時間的凈效益比類型1減少31%; 3) 類型3為失效后對所有裝備單元采取相同維修等級(假設所有裝備單元都采取第2個維修等級,v=2),其裝備系統(tǒng)最大單位時間的凈效益比類型1減少1%; 4) 類型4為將裝備的任務需求性能水平降為w=20%,其裝備系統(tǒng)最大單位時間的凈效益比類型1增加21%。 通過以上類比分析表明:筆者將裝備單元性能與裝備系統(tǒng)性能進行關聯(lián),考慮了不完全維修和裝備的任務需求性能水平,建立的權(quán)衡優(yōu)化模型可給出最優(yōu)的裝備單元維修與更換策略。 從維修實際出發(fā),對裝備單元進行不完全維修,采用裝備單元狀態(tài)的衰退速度衡量裝備單元的維修效果,建立考慮不完全維修的裝備單元維修與更換策略權(quán)衡優(yōu)化模型,并通過算例驗證了模型的有效性;利用該模型得出裝備系統(tǒng)的最優(yōu)維修費用與更換策略,既能保證裝備系統(tǒng)任務的順利完成,又可實現(xiàn)裝備系統(tǒng)單位時間的凈效益最大化,進而避免過度維修帶來的損失;裝備系統(tǒng)在運行中,當某一裝備單元狀態(tài)達到維修閾值時,將觸發(fā)維修機制。由于 裝備系統(tǒng)是由眾多裝備單元組成的,因此易造成裝備系統(tǒng)停機頻率高的問題,為此,下一步將結(jié)合機會維修策略進一步完善模型,解決復雜裝備系統(tǒng)因維修造成的停機頻率過高的問題。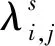


2.2 基于準更新過程的單元穩(wěn)態(tài)概率模型

2.3 維修成本與維修效果關系模型
2.4 考慮不完全維修的權(quán)衡優(yōu)化模型
3 算例分析


4 結(jié)論

