基于APSIM模型旱地小麥葉面積指數相關參數的優化

聶志剛，李廣，王鈞，馬維偉，雒翠萍，董莉霞，逯玉蘭

（1甘肅農業大學資源與環境學院，蘭州 730070；2甘肅農業大學信息科學技術學院，蘭州 730070；3甘肅農業大學林學院，蘭州 730070）

0 引言

【研究意義】作物生長模型是基于作物生長發育系統規律及原理，對系統成分及其相互關系的一種數學表達[1]。許多研究者有的放矢構建和引進作物生長模型[2-5]，為當地農作物生產的調控提供一定預測依據。模型的有效應用依賴于參數的快速、準確估算[6]。目前，模型參數的率定常采用窮舉試錯法[7-8]，該方法需要具有豐富農學知識和經驗的研究者基于長期田間試驗結果，手動調節來縮小實測、模擬值的誤差，率定過程中存在運算體量大、耗時長、精度低、效率低等突出問題[9]。作物生長模型參數優化的實質是對作物生長發育復雜生理生態系統的多目標優化問題。優化算法利用智能的學習策略，可在有限的迭代次數內對不確定、非線性、多維度的模型找到最優解，已廣泛應用于優化問題的解決[10]。【前人研究進展】近年來，國內外學者利用智能算法對作物生長模型參數進行了優化，MANSOURI等[11]將改進的粒子濾波算法用于更準確獲取作物生物量和蛋白質含量模型參數中；CALMON等[12]針對土壤水分平衡模型，利用模擬退火算法快速、準確獲得參數估算值；DAI等[13]通過嵌套兩級遺傳算法，提升了溫室黃瓜生長模型參數的估算能力；莊嘉祥等[6]利用個體優勢遺傳算法，快速、準確獲得了水稻生育期模型參數估算值；劉鐵梅等[14]將遺傳模擬退火算法應用于大麥葉面積指數模型參數的估算，效果良好。具有自學習等特征的啟發式智能算法，可實現模型參數的自動率定，提升了調參效率[6]，在一定程度上克服了參數率定過程存在的運算量大、耗時長、精度低等缺點。然而，算法原理及復雜度的不同使得運用效果各有差異，采用單個個體進化原理的模擬退火算法較群體優化算法運算量要大、速度也慢[15]。群體優化算法中，粒子群算法描述了微粒群在搜索空間中以一定速度飛行的互動行為，在進化后期收斂速度變慢，粒子趨于同一化，易陷入局部極值點，優化精度較差[10]；遺傳算法將生物進化過程中適者生存規則與群體內部染色體的隨機信息交換機制相結合[16]，搜索前需要對參變量集以特定形式進行編碼，操作復雜。作物生長模型參數優化過程中存在運算量大、耗時長，收斂值偏差及操作復雜等問題仍有待進一步解決[9]。2003年，EUSUFF等[17]首次提出混合蛙跳算法（shuffled frog leaping algorithm，SFLA），該新型算法模仿青蛙種群按照族群分類進行覓食行為思想傳遞的過程，族群內局部搜索使行為思想在族內青蛙個體間傳遞，族群間混合實現全局行為思想交流[10]；即相對獨立又合作協調的局部深度搜索和全局信息交流策略有效提高了運算的速度，使得算法跳出局部極值的能力增強，且算法參數設置較少，SFLA針對作物生理生態系統復雜模型的求解具備一定的先進性。【本研究切入點】針對黃土丘陵區域，沈禹穎[2]、李廣[18-20]等利用澳大利亞農業生產模擬平臺 APSIM（agricultural production systems simulator），主要在旱地小麥生產氣候變化效應及水肥管理等方面開展模擬研究，模型參數率定亦采用窮舉試錯法，參數快速、準確估算限制了 APSIM 的應用，因此欲提升 APSIM 應用效果，迫切需要利用先進的智能算法增強參數快速、準確估算的能力。【擬解決的關鍵問題】小麥群體葉面積指數是APSIM模型的重要變量，其模擬精度直接影響著作物生長模型整體模擬效果的評價[14,21-23]，為了對APSIM模型在黃土丘陵區域旱地小麥生產過程的精確模擬和有效應用提供技術支持，本文立足于定西市安定區多點（李家堡鎮麻子川村和鳳翔鎮安家溝村）、多年（2002—2005年和2015—2017年）大田試驗數據以及該區歷史氣象資料，采用SFLA方法對 APSIM 模型中與旱地小麥葉面積指數相關的參數進行優化。

1 材料與方法

1.1 試驗設計

甘肅省定西市安定區地處甘肅省中部偏南，海拔2 000 m左右，黃土丘陵典型雨養農業區域，一年一熟制，以春小麥單作為主。土壤為黃綿土，土質綿軟，質地均勻。氣候屬中溫帶干旱、半干旱特征，≥10℃的年活動積溫2 200℃以上，年均日照時數2 400 h以上，年均降雨量385.0 mm，降水主要集中在7—9月，無灌溉條件。

大田試驗分別于 2002—2005年在定西市安定區李家堡鎮麻子川村（104°44′E，35°28′N），2015—2017年在鳳翔鎮安家溝村（104°38′E，35°35′N）進行，兩地相距30 km。耕作及田間管理方式同采用定西地區傳統耕作方式[18]，試驗小區面積分別為80 m2（20 m×4 m）和24 m2（6 m×4 m），保護行0.5 m，完全隨機區組設置，3次重復。供試品種均為春小麥“定西35”，播種期為每年的3月19日左右，播種量按當地常規量187.5 kg·hm-2，免耕播種機播種，播深7 cm，行距0.25 m。各處理施105 kg N·hm-2，105 kg P2O5·hm-2，肥料作為基肥播種時一次性施入。種植密度為4×106株/hm2，用于SFLA適應度函數計算所需小麥葉面積指數模擬值中小麥植株日葉面積指數潛在增量的預測。

1.2 數據采集與方法

分別在出苗—分蘗、分蘗—拔節、拔節—孕穗、孕穗—抽穗、抽穗—開花、開花—灌漿、灌漿—成熟生長階段采用長寬系數法[24]，3次測算植株葉面積指數（leaf area index，LAI），取平均值為該階段葉面積指數實測值，用于SFLA適應度函數計算所需小麥葉面積指數實測值。采用半微量凱氏定氮法[25]，每生長階段3次取樣測定植株葉片氮素含量（%），得該階段植株葉片氮素含量實測平均值，用于SFLA適應度函數計算所需小麥葉面積指數模擬值中氮脅迫對葉片生長影響系數的確定。

1.3 APSIM模型參數優化方法

1.3.1 SFLA方法原理 SFLA基本優化原理如圖 1所示，青蛙可跳躍范圍即為定義域空間，每只青蛙個體的位置即定義域空間中一解，青蛙種群全部落在定義域空間內；Group1、2、3、4……I……M表示第 1、2、3、4……

I……M個青蛙子群；食物即為使適應度函數出現極值的青蛙位置，Food1、2、3……K表示包含在子群內的第 1、2、3、……K個食物，Foodbest表示整體種群中使適應度函數出現最優極值的青蛙位置。青蛙種群被分為多個子群，各子群由多只青蛙個體組成；子群內局部深度搜索使覓食行為思想在個體間傳遞，即位置最差的個體不斷的向子群或整體種群中位置最好的個體學習，使得個體向食物密集方向不斷跳躍；子群間行為思想相對獨立，各子群經過規定次數局部深度搜索后所有個體混合，實現全局行為思想交流，使得個體能夠跳出食物局部密集的位置。如此，整體青蛙種群反復進化，向食物最密集的位置不斷逼近。

1.3.2 適應度函數構造 優化時，構造合理的適應度函數是SFLA方法的核心，適應度函數可將參數優化問題轉化為受限條件下使適應值滿足的青蛙搜索問題。以使研究區小麥葉面積指數多年（2002—2005年和2015—2017年）實測、模擬值間誤差盡可能小為目標，如公式（1）所示構造適合于解決APSIM模型旱地小麥葉面積指數相關參數優化問題的適應度函數。

式中，G(X)表示青蛙的適應度函數，LAIreal_j_i為小麥葉面積指數實測值；LAIsim_j_i為基于APSIM的小麥葉面積指數模擬值，j表示年份，i表示葉面積指數測算階段分別為出苗—分蘗、分蘗—拔節、拔節—孕穗、孕穗—抽穗、抽穗—開花、開花—灌漿、灌漿—成熟。

適應度函數中小麥葉面積指數模擬值通過對小麥主莖上的節數，葉片數的估算，進一步推導可得，具體推導方法如下所示[26]：

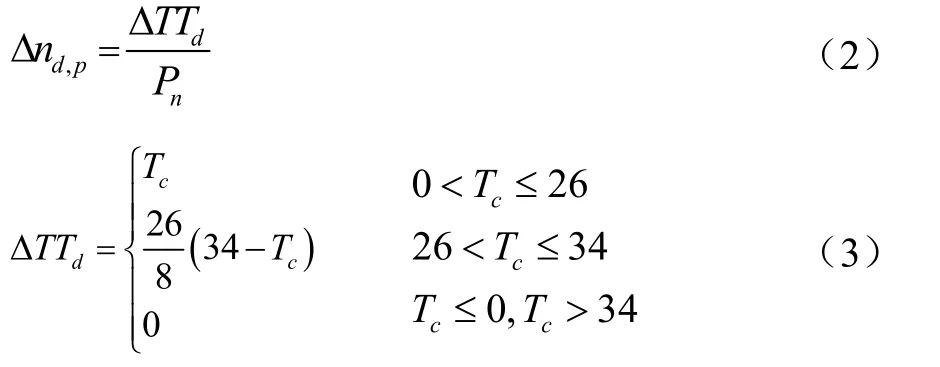
圖1 SFLA基本優化原理Fig. 1 Basic optimization principle with the shuffled frog leaping algorithm (SFLA)

式中，?nd,p為小麥植株日潛在節的增量；?TTd為某日生物學積溫（℃·d）；Pn為主莖上節出現所需的熱時間間隔。

根據RITCHIE等[27]在CERES-Wheat模型中關于日積溫的計算經驗，模型描述的日積溫算子與氣溫的關系如公式（4）、（5）和（6）所示。

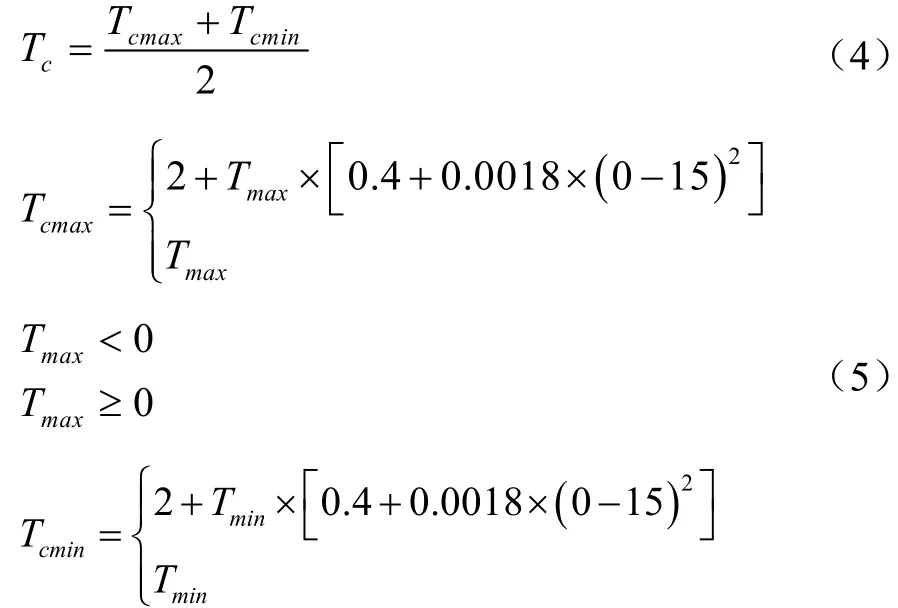
式中，Tc、Tcmax和Tcmin為日積溫算子平均值、最大值和最小值；Tmax和Tmin為日最高溫和最低溫，來源于氣象數據庫Dingxi.met。

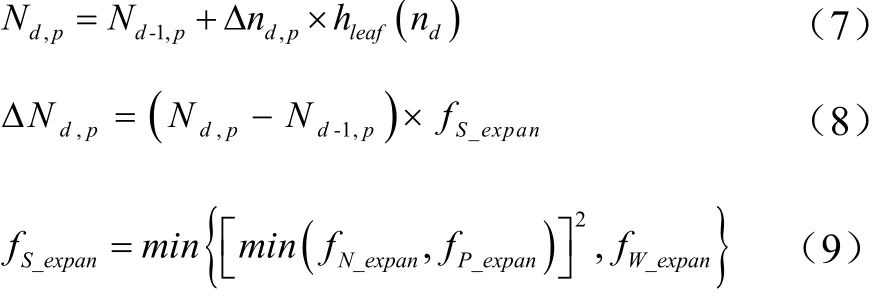
式中，?Nd,p為小麥植株日潛在葉片的增量；Nd,p為某日植株節上潛在葉片數量；Nd-1,p為前一日植株節上潛在葉片數量；hleaf(nd)為單節葉片增長函數，描述隨植株節數變化而變化的單節潛在葉片數，取值曲線封裝在APSIM內部；fS_expan為葉片生長脅迫系數；fN_expan為葉片氮脅迫系數；fW_expan為葉片水分脅迫系數；fP_expan為葉片磷脅迫系數，取值為1，說明模型假設磷素對葉片生長無影響。

氮脅迫對葉片生長的影響如公式（10）所示，根據實際進入植株葉片的氮素含量（%）計算。

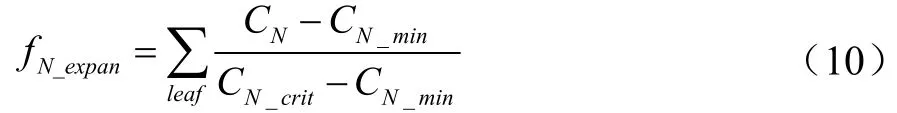
式中，CN為葉片實際氮素含量（%），葉片氮素含量實測平均值為0.53%（出苗—分蘗）、1.76%（分蘗—拔節）、3.78%（拔節—孕穗）、3.49%（孕穗—抽穗）、3.13%（抽穗—開花）、2.66%（開花—灌漿）和1.23%（灌漿—成熟）；CN_min為葉片自由生長結構性氮需求[26]下限（%）；CN_crit為臨界氮含量（%），反映了葉片試圖保留額外氮素的門檻。CN_crit和CN_min取值隨物候期變化曲線封裝于APSIM內部，假設研究區長年田間經驗施肥量滿足小麥葉片結構性氮需求[26]，即CN總是大于CN_min。

水分供應充足時，水分脅迫對葉面積指數沒有影響；水分供應不足時，葉片水分脅迫系數如公式（11）所示，以土壤水分供應量（Ws）與作物生長水分潛在需求量（Wd）的比值表示。

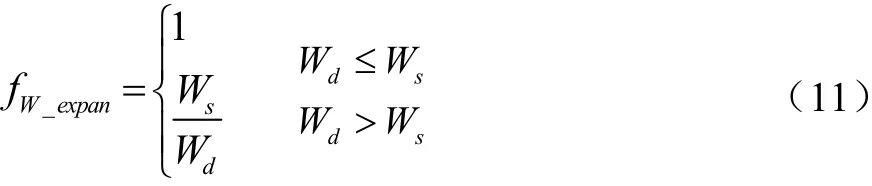
根據 SINCLAIR[28]和 MONTEITH[29]的研究，Ws與Wd由APSIM中水分平衡子模型計算。

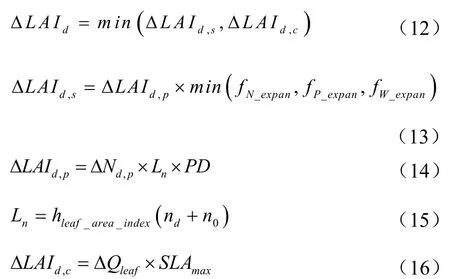
式中，?LAId為小麥植株日葉面積指數的增量；?LAId,s為環境脅迫下小麥植株日葉面積指數的增量；?LAId,c為同化物生產下小麥植株日葉面積指數的增量；?LAId,p為小麥植株日葉面積指數的潛在增量；PD為種植密度（plant/m2）；Ln為某日小麥植株節上葉片的潛在葉面積（mm2）；hleaf_area_index(nd)為單節葉面積增長函數取值曲線封裝于 APSIM 內部，描述隨植株節數變化而變化的單節潛在葉面積；nd為某日小麥植株上的節數；n0為某日正在生長的節數；ΔQleaf為日葉片干物質積累量（g），由APSIM中干物質積累與分配子模型動態計算；SLAmax為最大比葉面積（mm2·g-1），反映了單位面積的葉干重。

模型充分考慮了環境脅迫和同化物生產對葉片生長的生理生態過程。APSIM內部對小麥植株葉面積指數逐日累加，可得與實測時間相應的日葉面積指數模擬值，在出苗—分蘗、分蘗—拔節、拔節—孕穗、孕穗—抽穗、抽穗—開花、開花—灌漿、灌漿—成熟階段，每生長階段取平均值為該階段葉面積指數模擬值，即LAIsim_j_i。

1.3.3 SFLA方法實現 基于APSIM V7.7平臺，小麥生長模擬框架模塊的控制文件（Wheat.xml）采用XML語言實現，SFLA外掛優化程序集采用Visual C++ 6.0語言設計，程序流程如圖2所示，具體實現條件及做法如下：

（1）SFLA參數

參數包括子群內青蛙數（N）、青蛙子群數（M）、種群青蛙總數（P）、全局迭代次數（T1）、局部搜索次數（T2），取值為N=30，M=10，P=300，T1=300，T2=30。

（2）青蛙確定及可跳躍范圍

青蛙Y=(y1,y2,y3,y4,y5,y6)，其中(y1,y2,y3,y4,y5,y6)對應 APSIM-Wheat基本作物運行參數庫中與葉面積指數相關的6個待優化參數，分別是主莖上節出現所需的熱時間間隔、小麥出苗后初始化的節數、小麥出苗后初始化的葉片數、小麥出苗后初始化的葉面積指數、某日正在生長的節數、最大比葉面積。

小麥生長發育生理生態過程確定了待優化參數的定義域，即限制了青蛙可跳躍范圍。據陳國慶等[30]研究，小麥主莖上節出現所需的熱時間間隔80.0—100.0 ℃·d。據楊文雄[31]關于甘肅省旱地小麥審定品種農藝性狀2005—2014年的統計及甘肅省春小麥生長過程的研究和研究區長期定位試驗，小麥出苗后初始化的節數1.00—3.00、小麥出苗后初始化的葉片數1.00—3.00、小麥出苗后初始化的葉面積指數 0.050—0.130、某日正在生長的節數 1.00—3.00。劉鐵梅等[32]研究發現，小麥最大比葉面積22 000—45 000 mm2·g-1。

（3）種群初始化

以李廣等[18]通過窮舉試錯法得到的參數值為默認值，即主莖上節出現所需的熱時間間隔為95.0 ℃·d、小麥出苗后初始化的節數為2.00、小麥出苗后初始化的葉片數為2.00、小麥出苗后初始化的葉面積指數為0.080、某日正在生長的節數為2.00、最大比葉面積為26 000 mm2·g-1，以此為中心隨機產生300只青蛙進行種群初始化。

（4）分組輪換

按照適應度函數值對種群中青蛙個體降序排序，第1，2……M只青蛙對應分配到第1，2……M個子群，第M+1、M+2、……M+M只青蛙分配到第 1、2、……、M+M個子群，分組輪換直到P只青蛙全部被分配。

（5）局部搜索

SFLA子群內局部深度搜索流程如圖3所示，每次迭代過程，即將子群內Yworst(i)更新為Yworst(i+1)過程。第i次局部過程中，Ybest(i)、Yworst(i)和Yworst(i+1)分別為子群內適應值最優、最差和學習所得新青蛙，Yoverall_best(i)為整體種群中全局適應值最優青蛙。Yworst(i)向Ybest(i)學習步驟如公式（17）和（18）所示，如果Yworst(i+1)適應值優于Yworst(i)適應值，則Yworst(i)更新為Yworst(i+1)；否則，Ybest(i)替換為Yoverall_best(i)，Yworst(i)向Yoverall_best(i)繼續學習。如果Yworst(i+1)適應值仍未改進，則定義域內隨機生成一個Yworst(i+1)更新Yworst(i)。

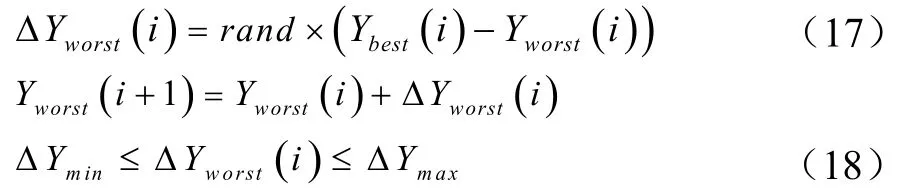
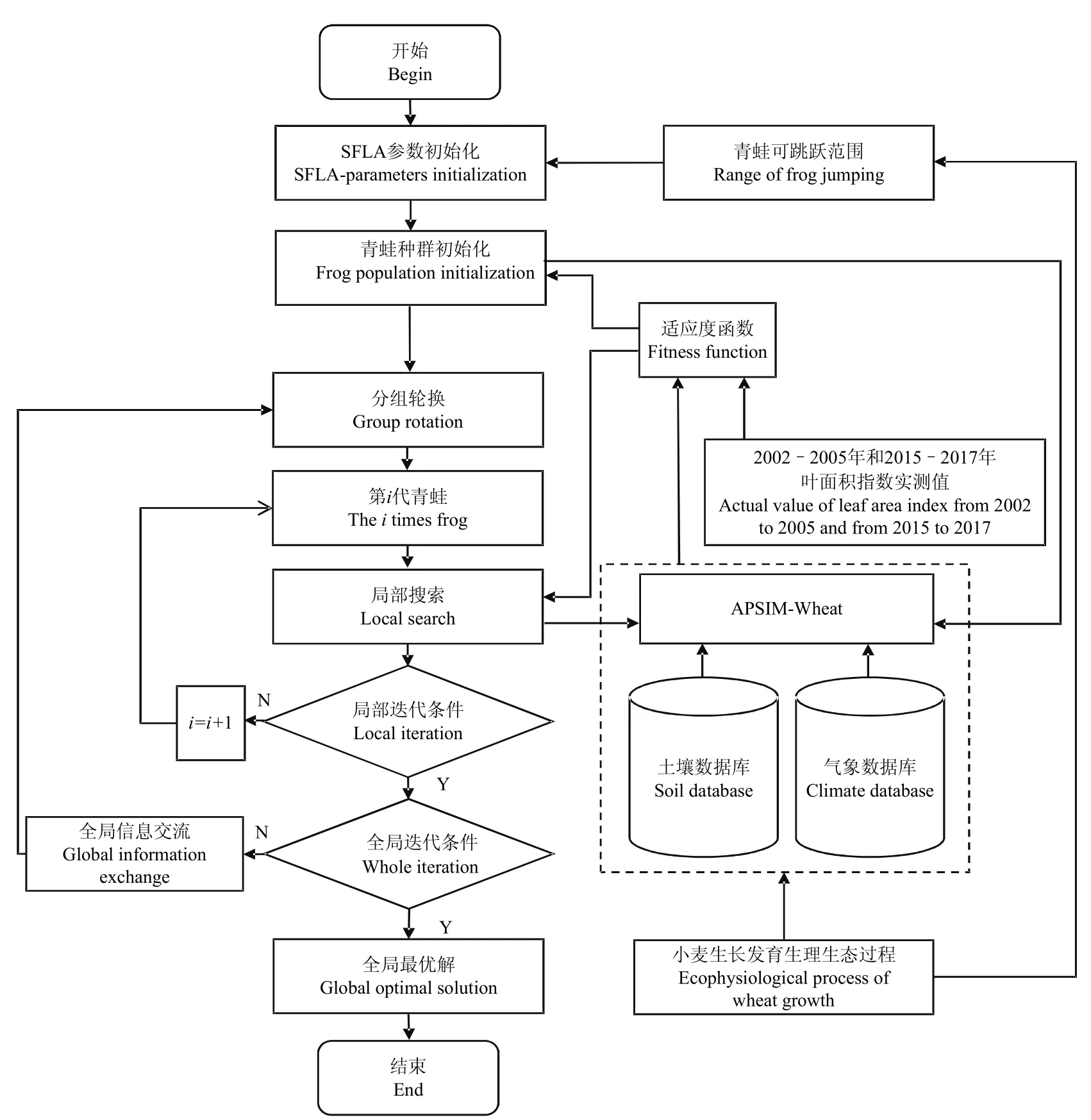
圖2 SFLA對APSIM模型旱地小麥葉面積指數相關參數優化流程圖Fig. 2 Flow-process diagram of optimization of the parameters related to dryland wheat leaf area index in the APSIM model with the shuffled frog leaping algorithm (SFLA)

圖3 SFLA子群內局部深度搜索流程圖Fig. 3 Flow-process diagram of local depth search with the shuffled frog leaping algorithm (SFLA) in sub-group

式中，i為局部迭代搜索次數，rand產生0—1之間隨機數，ΔYworst(i)為青蛙跳躍距離，ΔYmin和 ΔYmax為青蛙可跳躍范圍。

（6）全局信息交流

局部搜索次數滿足后，所有青蛙個體混合、降序排列、分組輪換，新子群繼續局部尋優，反復直到全局收斂條件滿足。

1.4 檢驗方法

實測值與模擬值的擬合度分析指標包括均方根誤差、歸一化均方根誤差及模型有效性指數，分別記為RMSE、NRMSE和ME，計算如公式（19）、（20）和（21）所示。RMSE和NRMSE值越小，實測值與模擬值誤差越小，擬合度越好[8]。ME介于0.5—1之間，則模型模擬效果較好，越接近1效果越好[33]。

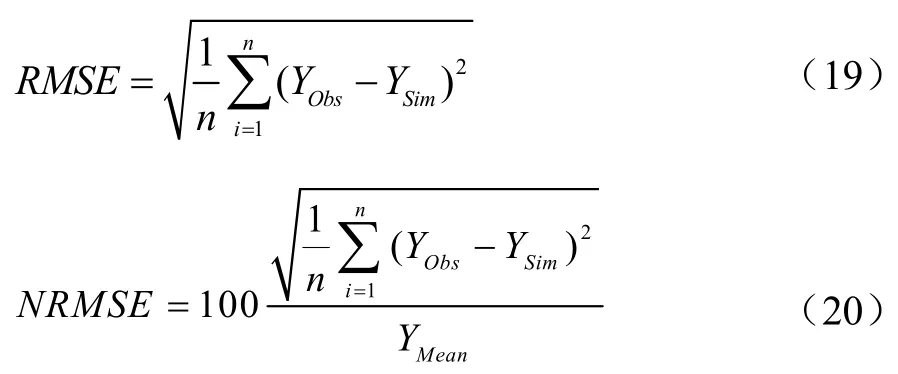
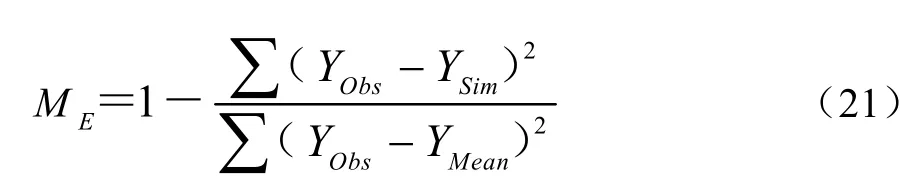
式中，YObs為實測值，YSim為模擬值，YMean為實測平均值。

2 結果

2.1 APSIM模型及相關初始參數確定

APSIM 是澳大利亞農業生產系統研究組（APSRU）開發的模塊化模擬平臺，用于模擬農業生產系統過程，有較廣的地域適用性，在作物生產氣候變化效應、水肥調控及農業氣象災害評價等領域有大量應用[2,18-22,34-36]。基于研究區土壤數據庫，在小麥生長模擬框架模塊（APSIM-Wheat）控制下，以氣象數據庫中逐日氣象數據為驅動變量，實現小麥生長發育過程以天為步長的動態模擬。本文基于田間試驗數據，參考李廣等[18]在黃土丘陵區 APSIM 適用性研究中通過窮舉試錯法得到的一系列參數，組建APSIM-Wheat基本作物運行參數庫。其中，與葉面積指數模擬相關參數包括主莖上節出現所需的熱時間間隔為95.0 ℃·d、小麥出苗后初始化的節數為2.00、小麥出苗后初始化的葉片數為2.00、小麥出苗后初始化的葉面積指數為0.080、某日正在生長的節數為2.00、最大比葉面積為26 000 mm2·g-1。

依據來源于甘肅省氣象局的1971—2017年定西市安定區歷史氣象資料組建氣象數據參數庫（Dingxi.met），包括最高氣溫（℃）、最低氣溫（℃）、太陽輻射量（MJ·m-2）和降水量（mm）。其中，太陽輻射量利用李廣等[18]對APSIM在黃土丘陵區適用性研究中日照時間轉換方法獲取。研究區土壤屬性數據用于APSIM 模型中小麥生長所需土壤環境的基本描述，參考李廣等[18]長期積累的黃土丘陵區適用性良好的相關土壤屬性數據，結合補充的田間試驗測定，組建研究區主要土壤屬性數據庫（Dingxi.soils），如表1所示。

表1 APSIM模型中研究區主要土壤屬性參數和小麥有效水分下限Table 1 Parameters of soil property and lower water limit of wheat in the experiment site used for APSIM model

2.2 旱地小麥葉面積指數相關參數優化結果

當T1=217時適應度函數開始收斂，T1=285時趨于穩定，全局最好青蛙即葉面積指數相關參數優化結果。以李廣等[18]通過窮舉試錯法得到的待優參數值為默認值，默認值與優化值比較如表2所示。其中，主莖上節出現所需的熱時間間隔、小麥出苗后初始化的節數、小麥出苗后初始化的葉片數、小麥出苗后初始化的葉面積指數和某日正在生長的節數為SFLA獲取的優化值；最大比葉面積反映了單位面積的葉干重，優化前假設其為一恒定值[23]，考慮到葉面積與逐日碳同化過程的密切聯系[26]，需要進一步優化，將最大比葉面積抽象為隨葉面積指數逐日變化的線性函數，即hSLA(LAId)函數。首先，以SFLA獲取的主莖上節出現所需的熱時間間隔、小麥出苗后初始化的節數、小麥出苗后初始化的葉片數、小麥出苗后初始化的葉面積指數和某日正在生長的節數優化值不變，定義域范圍內窮舉最大比葉面積，基于 APSIM 模型計算多年（2002—2005年和2015—2017年）出苗—分蘗、分蘗—拔節、拔節—孕穗、孕穗—抽穗、抽穗—開花、開花—灌漿、灌漿—成熟各階段葉面積指數模擬值，分別使得各階段多年實測、模擬值間誤差和最小的最大比葉面積值即為各階段該參數優化值；接著，采用線性回歸方法確定各階段最大比葉面積優化值與多年同階段葉面積指數模擬平均值關系及hSLA(LAId)函數，函數如圖4所示，在95%的置信區間內決定系數（R2）為0.9745，擬合程度較好。

表2 APSIM模型旱地小麥葉面積指數相關參數優化比較Table 2 Comparison between the SFLA optimized and default values of parameters related to dryland wheat leaf area index in the APSIM model

圖4 旱地小麥最大比葉面積與葉面積指數關系Fig. 4 Relationship between maximum specific leaf area and leaf area index of dryland wheat

研究區多點（李家堡鎮麻子川村和鳳翔鎮安家溝村）、多年（2002—2005年和2015—2017年）小麥葉面積指數實測、模擬值關系如圖5所示，表明APSIM模型分別使用試錯法所得默認參數和SFLA所得優化參數模擬葉面積指數，模擬結果均分布在-15%—+15%誤差線內，但使用優化參數模擬時數據點更趨于1∶1線，一致性更好。

采用RMSE、NRMSE及ME對研究區多點、多年葉面積指數田間實測值與模型模擬值擬合程度進行分析，由表3可知，麻子川村模擬結果的ME由0.983提高到0.993，安家溝村模擬結果的ME由0.974提高到0.992，平均值由0.979提高到0.993，表明使用優化參數使得模型模擬效果更好。麻子川村模擬結果的RMSE由0.047減小到0.031，NRMSE由7.06%減小到4.53%；安家溝村模擬結果的RMSE由 0.090減小到0.023，NRMSE由9.12%減小到4.59%；RMSE平均值由0.069降低到0.027，NRMSE平均值由8.09%降低到 4.56%，表明使用優化參數使得模型誤差更小，擬合程度更好。綜上所述，相對于窮舉試錯法，利用SFLA進行APSIM模型中與旱地小麥葉面積指數相關參數的優化，使得模型對研究區小麥葉面積指數的估算更準確。

表3 旱地小麥葉面積指數模擬檢驗結果Table 3 Test results of simulation on the leaf area index of dryland wheat

圖5 旱地小麥葉面積指數實測值與模擬值關系Fig. 5 Relationship of observed and simulated value on the leaf area index of dryland wheat

3 討論

研究區多點、多年旱地小麥葉面積指數實測值對優化前后模擬值驗證結果證明，模型參數優化后應用效果好于之前。參數優化后，模擬值均方根誤差平均值由0.069降低到0.027，歸一化均方根誤差平均值由8.09%降低到4.56%，模型有效性指數平均值由0.979提高到0.993。這是因為子群間多次全局信息交流，有效避免了子群內局部極值。具有自發學習特征的智能迭代行為，實現了參數的自動率定，提高了效率[6]。而且優化過程中SFLA方法通過先排序再分組輪換入群的策略，將解空間劃分為多個青蛙子群，子群內搜索方向為最優個體指引方向[10]，子群間尋優迭代運算全局協同，搜索方向的明確和協同合作的多源使得運算量得到控制，收斂速度加快；同時由于種群初始值選取前期窮舉試錯法得到的默認值[18]，避免了初始青蛙隨機取值所引起的盲目搜索，對收斂速度的加快有一定貢獻。

SFLA方法利用青蛙群體智能的生物進化學習策略，可實現對 APSIM 模型旱地小麥葉面積指數相關參數的快速、準確及高效估算。小麥出苗后初始化的葉片數、小麥出苗后初始化的節數、小麥出苗后初始化的葉面積指數和某日正在生長的節數，優化后均在甘肅省旱地小麥品種農藝性狀研究[31]中的合理范圍內，與研究區旱地小麥生理生態狀況相符。最大比葉面積受品種、溫度、光照、水分、CO2濃度及栽培管理等多種因素影響且相關影響機理還不十分清楚，估算困難[14,37]。優化前模型采用作物生長模型的一般做法，假設最大比葉面積為一恒定值[23]，由于該參數的敏感性容易造成葉面積指數模擬的較大誤差，所以近年來許多研究者將該參數抽象為植株年齡和溫度，或生育時期和植株密度，或其他環境影響因素的函數[38-39]。本研究中首先利用SFLA方法確定其他相關參數，接著分不同生育階段對最大比葉面積進行估算，最后建立最大比葉面積與葉面積指數之間的逐日連續線性關系，并將該線性取值封裝在 APSIM 內部，模擬結果顯示這種探索性的嘗試，為葉面積指數的動態逐日累加，提供了更為準確的計算依據。

作物生長發育是一個復雜的生理生態系統過程，基于 APSIM 的旱地小麥生長模型在以小麥生長模擬框架模塊（APSIM-Wheat）為核心的約束下，將小麥品種遺傳特性、作物生長發育進程、植株形態與產量形成等屬性、事件和過程[40]抽象描述為多個有窮數學子模型，并得到各子模型相應受限參數簇，包括生育期、干物質積累與分配、產量形成、葉片生長、根系生長、水分平衡、氮素平衡等子模型。APSIM-Wheat控制文件中建模語言采用可擴展標記語言（XML），以 XML格式存儲的代碼文檔，可分成許多獨立的部分并加以標識，使得小麥生長各子模型既具備統一的描述方法又擁有獨立進行數據交換的能力；APSIM平臺運行時，APSIM-Wheat的控制文件、氣候參數庫和土壤參數庫之間傳遞的都是簡單的字符流，經協議相同的XML解析器解析后，根據不同的XML標記，對數據的不同部分進行區分處理，從而使得基于APSIM的旱地小麥生長模型中各子模型的運行既協調統一又相對獨立。旱地小麥生長模型參數優化問題的實質是APSIM下對各子模型參數的多目標協同優化問題，因此可以利用線性加權將多目標優化問題轉化為多個單目標優化問題[41]。葉面積指數是作物葉生長的最終表征，葉面積指數模擬是葉片生長子模型的重要輸出之一，對其相關參數的單目標優化將為后續開展的旱地小麥生長模型的多目標協同優化提供重要的技術支撐。

本研究目前僅僅局限于單地區單品種，今后需要依據不同旱作農業區，選用多代表性品種，在不斷積累田間試驗數據的基礎上，進一步提高該優化方法的普適性。

4 結論

將SFLA方法應用于APSIM模型中與旱地小麥葉面積指數相關參數的優化，效果良好。相對于參數率定常用窮舉試錯法，模型參數優化后，模擬值均方根誤差平均值由0.069降低到0.027，歸一化均方根誤差平均值由 8.09%降低到 4.56%，模型有效性指數平均值由0.979提高到0.993，葉面積指數模擬精度顯著提高。本文將APSIM模型與SFLA方法進行耦合，并應用于旱地小麥葉面積指數相關參數的優化，為改善模型參數率定過程存在的運算量大、耗時長、精度低、效率低的缺點提供了一種行之有效的方法，對APSIM模型的精確模擬和有效應用提供了技術支持。