基于高斯擴散模型的重金屬污染源求解
高 振,房 越
(南京郵電大學,江蘇 南京 210003)
1 問題背景重述
近年來,人們對查證城市土壤地質環境異常、評價城市環境質量,研究人類活動影響下城市地質環境的演變模式等問題變得日益關注。根據文獻[1]所給的附件采樣點的位置海拔高度、主要重金屬元素濃度分析重金屬污染物的傳播特征。建立模型確定污染源的位置。
2 模型的建立與求解
2.1 基于高斯擴散模型的偏微分方程的建立
Step1:正態分布的確定。采用統計學方法研究污染物質在土壤中的傳播擴散模型[2]。如果從原點釋放出一堆粒子,經過一段時間T之后,濃度區域一個穩定的狀態。粒子呈現正態分布,如下圖所示其滿足的形式滿足:


圖1 正態分布圖
其中f( y )代表粒子的概率密度,σ為此方向上的傳播標準差,μ為概率密度最大的點,即濃度最大的點,即傳播源所在的位置。
Step2:連續點源的擴散方程。假設污染物在傳播的途中滿足一下幾個條件:
①土壤流場穩定,傳播速度均勻;②金屬污染物在x,y,z方向上滿足正態分布;③金屬污染物在傳播的途中滿足質量守恒;④污染源強連續均勻。得出如下的方程:

其中f( x, y, z )代表粒子的概率密度,σx, σy,σz分別為x, y, z上的傳播標準差,(x0,y0,z0)為概率密度最大的點,即濃度最大的點,即傳播源所在的位置。
Step3:污染濃度求解。已知從一定量的金屬污染物粒子從傳播點擴散的概率密度方程。概率密度與在污染源點存在的污染物濃度相乘,得到在每一個點的金屬污染物的濃度,則測試點(x, y, z)的污染物濃度如下(Q為污染源處的濃度):
c(x ,y,z )=Q ×f(x,y,z )
我們可以得到在測試點(x, y, z)的最終的污染物濃度表達式:

Step4:簡化方程。

然后對兩邊同時取對數,得到化簡后的方程為:

2.2 污染源范圍的確定
根據附件中的數據得到的污染物三維立體圖上顏色較深的區域,找出區域的的坐標及其對應的編號,即為污染較嚴重的區域。砷的污染源在樣本點84,18附近。
2.3 非線性最小二乘法
結合我們已經求出的金屬污染物傳播方程,其為非線性多元函數。要求出其中的未知參數,我們選擇用非線性最小二乘法。求解非線性最小二乘,其導數形式太過于復雜無法直接寫出,我們通過不停的迭代計算尋找到函數的局部最小值,并認為該局部最小值能夠使得我們的要求解的函數取得最優解。
Step1:局部最小值。非線性最小二乘問題形式,下面稱為代價函數:
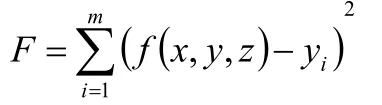
同時定義局部最小值為,對于代價函數F,有變量滿足:
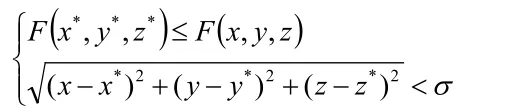

中,當x1, y1, z1分別代表x, y, z。求出所有滿足該函數一階導等于零的點,得駐點:

綜上所述,局部最小值為函數的駐點,但是駐點也有可能是函數的局部最大值或者鞍點。為了區分到底是局部最小值、局部最大值或者是鞍點,我們保留泰勒展開式的二階信息。通過判定展開式中的矩陣的相關性質進行判定:
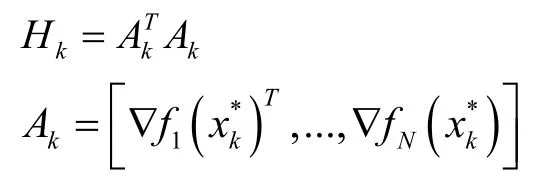
當該矩陣為正定矩陣時,所求駐點是局部最小值。
Step2:運用算法求解最小二乘問題。
因高斯牛頓法中的泰勒展開只有在展開點附近才會有比較好的效果,因此為了確保近似的準確性我們需要設定一個具有一定半徑的區域作為信賴區域。我們需要明確信賴區。在L-M算法中信賴區大小的確定也是運用增益比例來進行判定的。基于信賴區域能夠重新構建更有效的優化框架。引入拉格朗日乘子將有約束優化問題轉化為無約束優化問題。求出L-M算法增量表達式。通過MATLAB中“nlin fit”函數可以直接調用這種方法,求出的As金屬的污染源坐標[18122,9315]、[12930,3400]。

