問題解得清如許 為有源頭析得深

金玲玲

(浙江省臺州中學 318000)

一、 提出問題，穿針引線

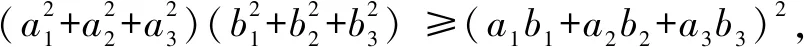
生：已知a2+b2+c2=1,求a+b+c的最大值.(解略)

筆者認為讓學生自己出題可大大提高學生的學習興趣，也可進一步檢驗學生掌握知識的能力和水平.前蘇聯心理學家維果斯基認為，學生的思維發展水平可以區分為兩種，一種是現有發展區，這是教學的出發點；第二種是最近發展區，它是一種潛在的、可能的發展水平，只有經過教師不斷地啟發指導和學生自己努力所能夠達到的發展水平，這才是教學所應該努力追求的目標.本節課開門見山地提出課題的中心并要求學生自己出題，而恰恰這樣的啟發，讓學生處于“跳一跳摘果子”的狀態，不僅可以解決問題，而且又能激發學生的求知欲.

二、局部調整，深入探究

師：變式1.條件不變，求a+2b+3c的最大值.

變式2.條件不變，求a-2b+3c的最大值.

變式可以先在條件不變的情況下，改變另一些條件的形式，使問題進一步簡單地深化.變式的目的使學生有機會親歷習題發生“化學變化”，進而理解其本質特征，進一步提高學生的創新能力和解決分析問題的能力.

師：你能將條件一般化嗎？題目形式又會發生怎樣的變化呢？

生：變式3.已知條件改為2a2+3b2+5c2=1，求a+b+c的最大值.

生：變式4.已知條件改為2(a-1)2+3(b-2)2+5(c-3)2=1，問題同上.

生：變式5.已知a+b+c=1,求a2+b2+c2的最小值.

生：變式6.變式5的條件不變，求a2+4b2+9c2的最小值.

生;變式8.求(a-1)2+4(b-2)2+9(c-3)2的最小值.

筆者以為以上選擇的習題非常具有典型性.華羅庚先生曾經講過，學習數學有兩個過程，其一是由薄到厚，其二是由厚到薄.而在高三的復習過程中，我們需要選擇后者.這勢必要求我們充分發揮試題的教學功能，讓變中出彩，讓“源頭”豐富起來，從而讓習題“源遠流長”.

三、更換條件，聲東擊西

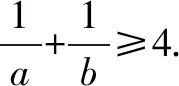
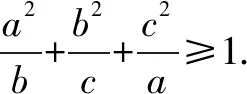
變式6 試改變條件，設計出其他的問題.

在中學數學習題變式教學中，對習題的變式要循序漸進，有的放矢.變式在于對某種方法的深刻認識和鞏固.有位特級教師說過：“如果知識的背后沒有方法，知識只能是一種沉重的負擔；如果方法的背后沒有思想，方法只不過是笨拙的工具.”就數學學習而言，學生的智慧集中體現在對數學思想方法的深刻領悟和自覺運用上，可以說領悟與運用數學思想方法的過程就是學生智慧生長的過程.所以，一堂課的題目不在于多，而在于精，要在選題上做到以少勝多.作為教師，我們更要教會學生順藤摸瓜，擴大成果，做到舉一反三，觸類旁通.所以我上一系列變式設計目的在于，讓學生對似曾相識的題目回顧，易聯想到構造公式所需要的結構，從而靈活運用柯西不等式.而以上6點使用柯西不等式進行變式，一氣呵成，思路自然，不偏不怪，又展示出試題”柔“的一面，貯存著豐富的內涵，又有良好的區分度.

四、改頭換面，剛柔并濟

在習題變式教學中，對習題的變式要注意縱向聯系，讓學生在學習新知識的同時對舊知識也得到復習，讓學生明白“任何事物都是相互聯系的”這一哲學道理.

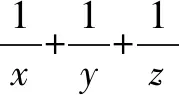
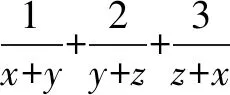
師：我們可順勢延展到2009浙江高考03號題 已知正數x，y、z滿足x+y+z=1.

(2)求4x+4y+4z的最小值.

五、教學反思

G·波利亞早就指出：“解題的價值不是答案的本身，而在于弄清‘是怎么樣想到這個解法？’‘是什么促使你這樣想，這樣做的’.”這就是說，解題過程是一個思維過程，是一個把知識與問題聯系起來思考、分析、探索的過程，是教師引導學生“用自己的頭腦親自獲得知識的再發現過程”.本課的設計始終貫徹讓學生認清柯西不等式的本質結構，積極引導讓學生交流思考，構造不等式，由此，冰冷的知識被思維過程所點燃，思維的障礙經概念理解而飛躍，優美的解法被數學思想駕馭，知識的運用和知識的產生得以同步發展.