基于EMD和Hilbert包絡(luò)譜分析的滾動(dòng)軸承故障診斷研究

重慶交通大學(xué) 機(jī)電與車輛工程學(xué)院 重慶 400074

1 研究背景

滾動(dòng)軸承是旋轉(zhuǎn)機(jī)械中的重要零部件,也是最容易損壞的零部件。滾動(dòng)軸承發(fā)生故障,將會(huì)對(duì)設(shè)備造成非常大的影響。因此,對(duì)滾動(dòng)軸承的故障診斷技術(shù)進(jìn)行研究,有十分重要的意義[1-2]。滾動(dòng)軸承故障常用的診斷方法有經(jīng)驗(yàn)?zāi)B(tài)分解(EMD)方法、短時(shí)傅里葉法、小波分析法等[3-4]。Norden E Huang等人在1998年提出對(duì)非平穩(wěn)信號(hào)進(jìn)行EMD,將其分成一系列本征模態(tài)函數(shù)(IMF),隨后再通過Hilbert變換獲取整個(gè)信號(hào)頻譜[5]。張志剛等[6]提出一種改進(jìn)的EMD方法,對(duì)信號(hào)的前期處理進(jìn)行優(yōu)化,但有較大的局限性。喻洋洋等[7]提出應(yīng)用LabVIEW軟件建立滾動(dòng)軸承故障診斷系統(tǒng),但缺乏必要的試驗(yàn)驗(yàn)證。孟宗等[8]提出基于壓縮感知的方法來提取故障信息,但對(duì)硬件的采集及傳輸?shù)确矫嬉筝^高,實(shí)現(xiàn)條件較為復(fù)雜。郝高巖等[9]提出一種改進(jìn)階次包絡(luò)譜分析方法,這一方法對(duì)獲取的信號(hào)進(jìn)行包絡(luò)分析后,再對(duì)信號(hào)進(jìn)行濾波處理,能夠較好地提取故障信息,但所需要的計(jì)算量較大,有較大的局限性。

上述方法都存在較大的局限性。為實(shí)現(xiàn)滾動(dòng)軸承故障的檢測(cè)與診斷,筆者針對(duì)滾動(dòng)軸承的振動(dòng)信號(hào)采用EMD方法,得到滾動(dòng)軸承的IMF分量,再對(duì)這些IMF分量進(jìn)行Hilbert包絡(luò)解調(diào)分析,由此得到滾動(dòng)軸承的故障特征信息,實(shí)現(xiàn)滾動(dòng)軸承的故障診斷。

2 EMD概述

EMD方法本質(zhì)是對(duì)信號(hào)的平穩(wěn)化處理,尤其適用于非線性、非平穩(wěn)信號(hào)的處理。這一方法可以將復(fù)雜非線性信號(hào)分解為有限個(gè)IMF分量[10],每個(gè)IMF分量必須滿足兩個(gè)條件[11]:一是在整個(gè)信號(hào)時(shí)域內(nèi)的極點(diǎn)數(shù)與零點(diǎn)數(shù)相等,或者最多相差1;二是在信號(hào)上任意取一點(diǎn),局部最大值所確定的包絡(luò)線與局部最小值可確定的包絡(luò)線均值為0。

對(duì)任何信號(hào)進(jìn)行EMD時(shí),對(duì)原始信號(hào)x(t)上的所有極大值點(diǎn)和極小值點(diǎn)分別采用三次樣條函數(shù)進(jìn)行擬合,所得到的兩個(gè)函數(shù)擬合曲線作為原始信號(hào)x(t)的上下包絡(luò)線。計(jì)算出它們的平均值,記為m1(t)。將原始信號(hào)x(t)與m1(t)相減,得到新的信號(hào),記為h1(t):

h1(t)=x(t)-m1(t)

(1)

如果信號(hào)h1(t)不滿足IMF的兩個(gè)條件,那么需要將h1(t)作為原始信號(hào)重復(fù)上述步驟,篩選k次,直到信號(hào)h1k(t)滿足IMF分量的兩個(gè)條件,信號(hào)h1k(t)變?yōu)榈谝粋€(gè)IMF分量:

h1k(t)=h1(k-1)(t)-m1k(t)

(2)

式中:h1(k-1)(t)為篩選k-1次后的信號(hào);m1k(t)為篩選k次后的上下包絡(luò)線函數(shù)平均值。

由原始信號(hào)中分解得到一階IMF分量,記為c1(t):

c1(t)=h1k(t)

(3)

從原始信號(hào)x(t)中減去c1(t),得到第一階剩余信號(hào),記為r1(t):

r1(t)=x(t)-c1(t)

(4)

再將r1(t)作為原始信號(hào),重新按照式(1)～式(3)計(jì)算,得到第二個(gè)IMF分量c2(t)。

重復(fù)以上步驟,可以得到c3(t)、c4(t)、…、cn(t),直至rn(t)不能再被分解或者是滿足給定的終止條件。通常rn(t)成為一個(gè)單調(diào)殘余函數(shù)時(shí)退出循環(huán),于是有:

(5)

式中:rn(t)代表信號(hào)的平均趨勢(shì)。

3 Hilbert包絡(luò)譜分析概述

Hilbert變換時(shí),使測(cè)試信號(hào)產(chǎn)生一個(gè)90°的相移,從而與原信號(hào)構(gòu)成一個(gè)解析信號(hào),這個(gè)解析信號(hào)即為包絡(luò)信號(hào)。

將一個(gè)原始信號(hào)x(t)的Hilbert變換H[x(t)]定義為:

(6)

H[x(t)]可以看作是x(t)通過濾波器的輸出,則原始信號(hào)x(t)的解析信號(hào)z(t)可以表示為實(shí)部和虛部形式:

z(t)=x(t)+jH[x(t)]

(7)

Hilbert變換后的信號(hào)幅值記為a(t),a(t)定義為:

(8)

瞬時(shí)相位Φ(t)定義為:

(9)

由上述步驟可知,EMD方法所分解得到的IMF分量可以通過幅度或者頻率進(jìn)行調(diào)制,再通過Hilbert變換將信號(hào)高頻振動(dòng)分量去除,用含有缺陷激勵(lì)分量的a(t)代替原始信號(hào)x(t)進(jìn)行頻譜分析,這樣就可以有效提取故障信息,進(jìn)行故障診斷。

4 滾動(dòng)軸承故障診斷

筆者所研究的滾動(dòng)軸承型號(hào)為6205,外徑為52 mm,內(nèi)徑為25 mm,軸承節(jié)圓直徑D為39 mm,滾動(dòng)體直徑d為7.938 mm,滾動(dòng)體數(shù)量Z為9,軸承轉(zhuǎn)速n為1 772 r/min,接觸角α為0°,數(shù)據(jù)采樣頻率為12 000 Hz。

軸承內(nèi)圈故障頻率f為:

(10)

計(jì)算得到軸承內(nèi)圈故障特征頻率為159.95 Hz。

對(duì)軸承故障振動(dòng)信號(hào)進(jìn)行處理,得到故障振動(dòng)信號(hào)時(shí)域圖,如圖1所示,同時(shí)得到頻譜圖,如圖2所示。

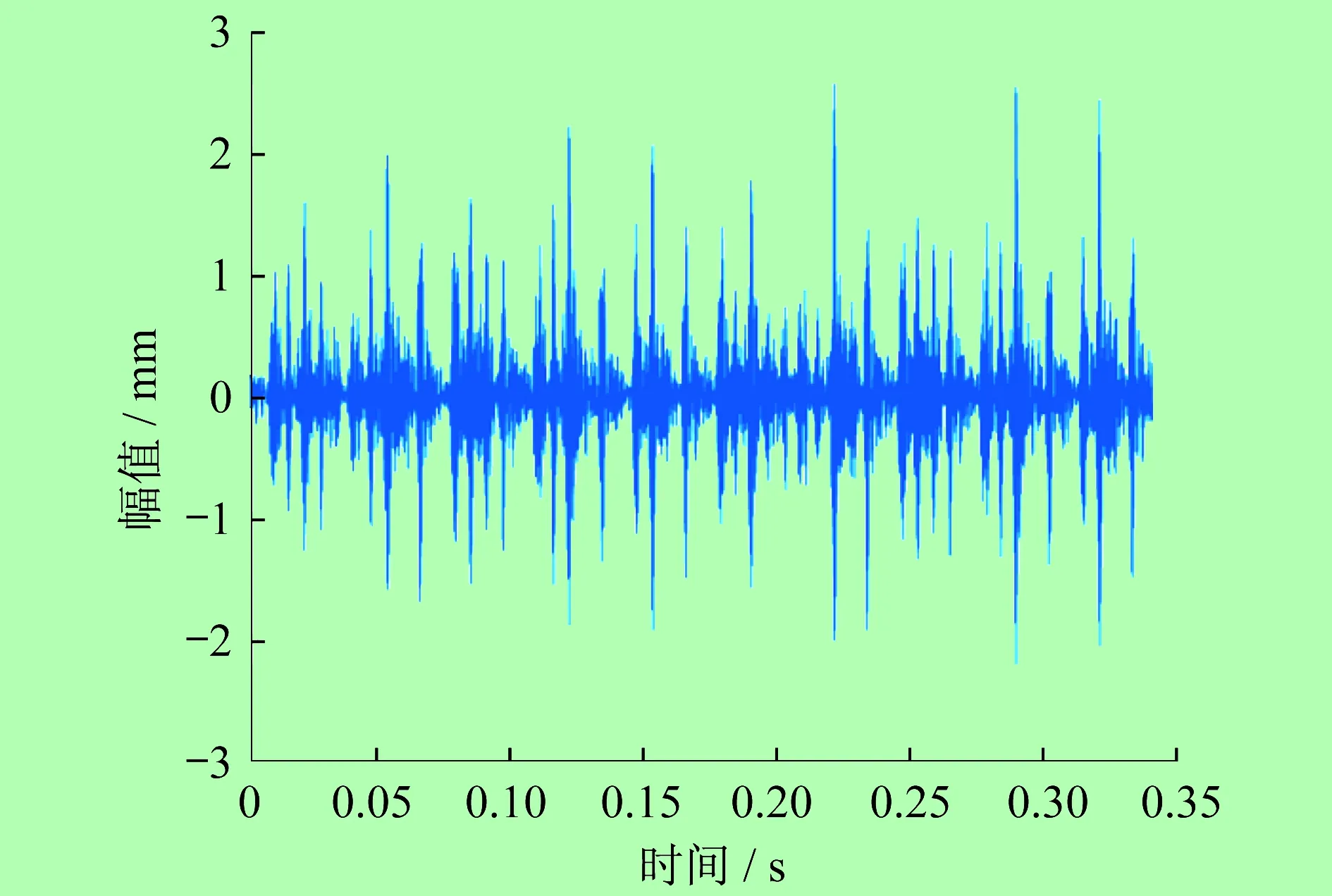
圖1 故障振動(dòng)信號(hào)時(shí)域圖

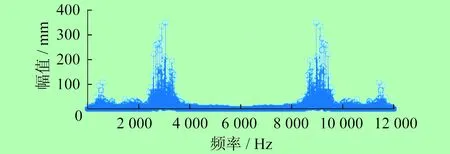
圖2 故障振動(dòng)信號(hào)頻譜圖

對(duì)滾動(dòng)軸承故障振動(dòng)信號(hào)采用EMD方法分解,得到各階IMF分量,如圖3所示。

基于EMD后得到的IMF分量,通過信號(hào)相關(guān)因數(shù)求解方程,可以計(jì)算出各階IMF分量與原始信號(hào)的相關(guān)因數(shù),見表1。

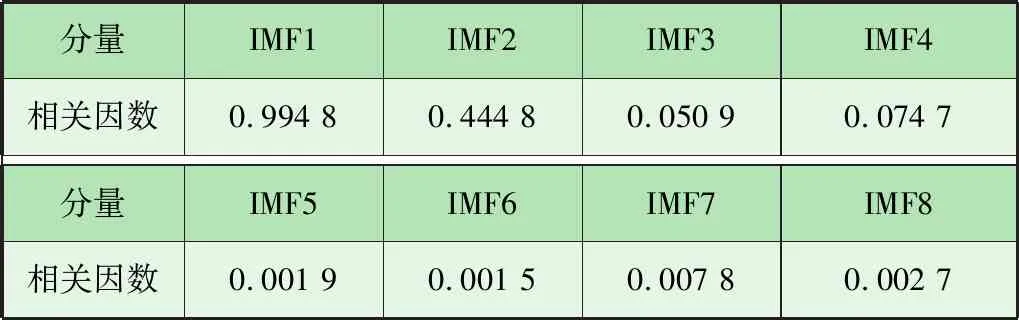
表1 各階IMF分量與原始信號(hào)相關(guān)因數(shù)

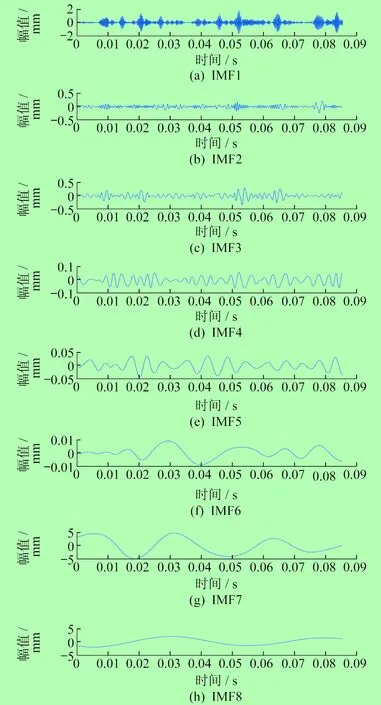
圖3 故障振動(dòng)信號(hào)各階IMF分量

由表1可以看出,IMF1分量與原始信號(hào)的相關(guān)因數(shù)最大,因此,選取IMF1分量進(jìn)行Hilbert包絡(luò)譜分析,分析結(jié)果如圖4所示。

由圖4可以看出,滾動(dòng)軸承的故障頻率為159.4 Hz,這與理論計(jì)算所得的滾動(dòng)軸承內(nèi)圈故障頻率159.95 Hz基本吻合。可見,所研究的滾動(dòng)軸承內(nèi)圈存在損傷。

5 結(jié)束語

筆者提出基于EMD與Hilbert包絡(luò)譜分析的滾動(dòng)軸承故障診斷方法,并對(duì)滾動(dòng)軸承進(jìn)行了故障診斷。這一方法通過EMD將非線性、非平穩(wěn)振動(dòng)信號(hào)分解出反映原始信號(hào)的IMF分量,應(yīng)用Hilbert變換得到包絡(luò)譜。試驗(yàn)結(jié)果表明,這一方法可以較為有效地獲取滾動(dòng)軸承的故障信息。

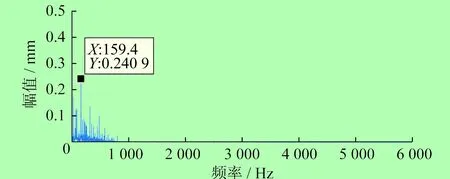
圖4 Hilbert包絡(luò)譜分析結(jié)果