基于量子游走的仲裁量子簽名方案*

馮艷艷 施榮華 石金晶 郭迎

(中南大學計算機學院,長沙 410083)

1 引 言

量子簽名是數字簽名的量子相對物.類似于經典數字簽名,依照仲裁的參與度,量子簽名區分為真實量子簽名(true quantum signature,TQS)和仲裁量子簽名(arbitrated quantum signature,AQS).在TQS算法中,簽名算法是隱秘的,驗證算法是暴露的.只有在產生糾紛或者分歧的時候,仲裁才被需求.在AQS算法中,簽名和驗證算法均為秘密的.仲裁作為可信任的第三方參與算法的設計和實現過程.盡管TQS是有利的,AQS被證明在電子投票和電子支付場景是更加實用的[1,2].因此,本文重點關注AQS.

隨著未來量子計算機[3]的出現,依據不可證明計算假設和許多難解數學難題的簽名算法將被攻破.而依據物理特性的量子密碼簽名算法是信息安全的,加之量子保密通信技術在理論和實驗上的不斷發展[4-8],許多學者們對AQS方案的研究一直密切關注.2002年,Zeng和Keitel[2]首次基于Greenberger-Horne-Zeilinger (GHZ)態提出AQS方案.2008年,Curty和Lütkenhaus[9]對文獻[2]方案的描述和操作給出了評論.同年,Zeng[10]對文獻[2]給出了一個詳細的證明并對文獻[9]給出了回應.2009年,Li等[11]使用Bell態代替GHZ態提出了相對應的AQS方案,并展示了其在傳輸效率和實現具有低復雜度的優勢.之后,研究者對AQS的安全性進行了深入研究.2010年,Zou和Qiu[12]宣稱已有的AQS方案不能保證來自接收者的抵賴,并設計了可以抵抗接收者抵賴的AQS算法.2011年,Gao等[13]指出基于量子一次一密(quantum one time pad,QOTP)的AQS方案中存在簽名的抵賴攻擊和接收者的偽造攻擊,并給出了相應的改進方法.同年,Choi等[14]強調已有AQS協議中存在一種通過修改傳輸消息和簽名的偽造攻擊,并提出了抵御這種攻擊的方法.2013年,張駿和吳吉義[15]建議了一種能夠抵抗驗證者已知明文攻擊的AQS協議.2015年,Li和Shi[16]使用鏈式受控非操作代替QOTP提出了AQS方案.2016年,Yang等[17]設計了基于簇態的AQS協議,其效率可以達到 1.2017年,Zhang等[18]設計了基于鍵控鏈式受控非(keycontrolled chained CNOT,KCCC)操作的改進的AQS方案.2018年,Zhang和Zeng[19]提出一個改進的基于Bell態 AQS方案.以上這些方案都是基于離散變量的AQS方案.在連續變量AQS協議方面,我們分別提出了基于相干態[20]和壓縮真空態[21]的AQS方案.

依據信息副本從簽名者到接收者被傳輸的方式,以上所提到的AQS協議可以分為兩類：1)基于糾纏態的隱形傳輸方式,例如GHZ[2]、Bell[11]、連續 Einstein-Podolsky-Rosen (EPR)[20,21];2)簡單的量子加密方式,例如QOTP[12]、鏈式受控非操作[16]、KCCC操作[18].第二種AQS協議又可以分為可以抵抗存在性偽造攻擊和不可以抵抗存在性偽造攻擊的協議.其中在基于QOTP的AQS[12-16]中,由于其一個比特對應一個比特的加密方式,簽名者能夠執行抵賴攻擊且接收者在已知信息環境下可以執行存在性偽造攻擊,基于KCCC算法的改進的AQS協議[18]可以較優地抵抗這兩類攻擊.相比于第二種信息傳輸方式,基于糾纏的量子隱形傳輸方式具有如下特性：第一,在傳輸過程中具有防竊聽功能,即一旦有竊聽者想要竊聽信息,測量引起的擾動會被誠實的參與者發現;第二,可以避免傳輸載體本身,只是轉移粒子所處的量子狀態;第三,不受物理距離的限制,普通的加密方式僅限在地區性的網絡上.因此,應用基于量子游走的隱形傳輸轉移信息副本和KCCC算法執行中間過程的加密傳輸,本文提出一種新型的AQS協議.

量子游走是經典游走的量子對應.1993年,Aharonov等[22]初次提出量子游走模型.量子游走在多個方面展示了有意義的應用(詳見綜述文獻[23,24]),其中量子游走在通信協議方面的應用[25-27]也開始暫露頭角.例如,近兩年,Wang等[25]和Shang等[26]提出了量子游走的不同模型在隱形傳輸的成功應用,文中指出必要的糾纏態無需提前制備,它們可以在量子游走的第一步之后被制備(相對于糾纏態的難以制備,這是一種很大的改進).而且,作者給出了一維量子游走的實現線路圖.由于量子游走已經被證明可以在多種不同的物理系統和實驗上實現[28-30],將其應用在量子通信協議中是有益的.

因此,本文通過將基于量子游走的隱形傳輸方式應用在AQS方案中傳輸信息副本,提出了基于量子游走的AQS方案.提出的方案具有以下優勢：1)糾纏態不必提前制備,量子游走的第一步會產生信息傳輸必需的糾纏態;2)KCCC操作和隨機數的應用可以抵抗已有AQS方案中的抵賴和存在性偽造攻擊,本方案滿足不可抵賴、不可偽造和不可否認特性;3)由于量子游走已經被證明可以通過現有的光學元素實現,提出的AQS方案實驗上也許是可實現的.

本文的結構如下：第2節描述基于圖的量子游走;第3節提出基于量子游走的AQS算法;第4節對提出的AQS算法給出安全性分析、討論以及比較;第5節為結論.

2 基于圖的量子游走

圖上基于硬幣的量子游走模型的定義由Aharonov等[31]給出.已知G=(V,E)為一個圖,V代表G的頂點集,E代表G的邊集.對于規則圖形,圖中的每個頂點具有相同的鄰居,其希爾伯特(Hilbert)空間可以表述為位置空間和硬幣空間的張量積,即

其中Hv是頂點態|v〉張成的Hilbert位置空間,其中v∈V.在每一個頂點j,有d條有向邊連接到其他的頂點,Hc是邊態|c〉張成的Hilbert硬幣空間,其中c ∈{0,···,d-1},它們用來標記有向邊.位置空間Hv和硬幣空間Hc之間的條件移算符可以表示為

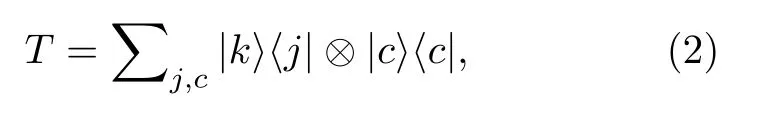
其中標簽c指示游走者從頂點j游走到頂點k.

考慮一個包含l(l=4)個頂點的圖(環),如圖1所示,頂點標記為0,1,2,3,構成量子游走的位置空間為在每個頂點有兩條邊,它們的標記分別為0和1,構成量子游走的硬幣空間為其條件移算符為

其中k代表環中的頂點.環上的相移規則見圖1.

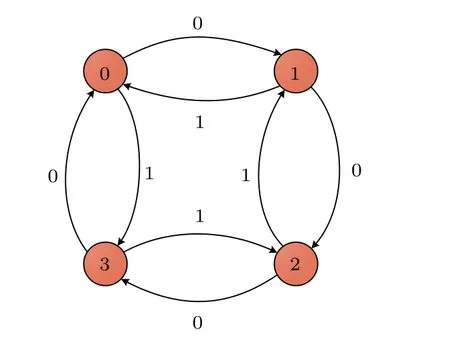
圖1 具有四個頂點的環及其相移規則Fig.1.Shift regulations on a cycle with four vertexes.

3 基于量子游走的量子簽名算法

本AQS算法中,Alice是信息的發送者和簽名者,Bob是簽名后信息的接收者和驗證者,Charlie是值得Alice和Bob信任的第三方仲裁.對于一個安全量子簽名算法[2],它應該遵循Alice對簽名后的信息和簽名的不可抵賴、任何人對Alice簽名的不可偽造和Bob對接收到的簽名信息或文件的不可否認特性.

3.1 初始化階段

1)密鑰制備和分發：Alice和Charlie制備共享密鑰Ka,Bob和Charlie制備共享密鑰Kb,Ka和Kb分別記為

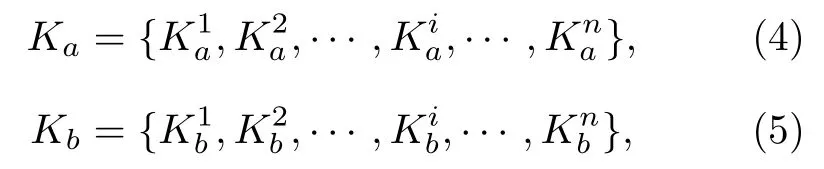
2)系統配置：當Alice和Bob需要通信時,Alice或Bob向Charlie申請通信.

3.2 簽名階段

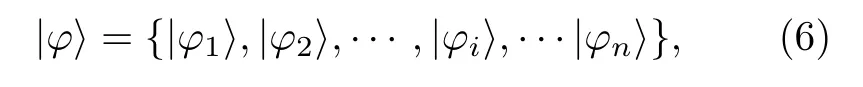
其中|φi〉(i=1,2,···,n)代表一個單量子比特,記為

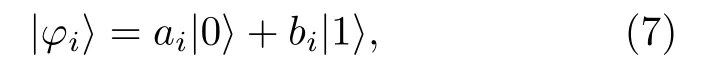
2)Alice選擇一個隨機數r,并用其變換|φ〉為秘密的信息序列|φ′〉,可記為

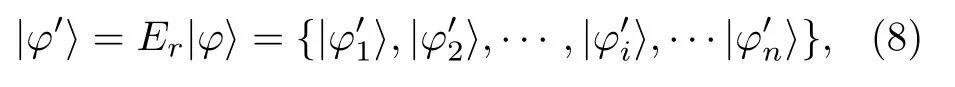
3)應用Zhang等[18]提出的KCCC算法,Alice使用密鑰Ka生成量子態|Sa〉,記為

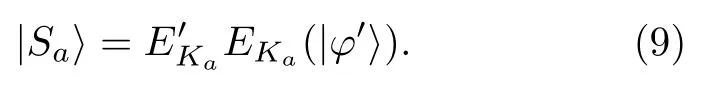
其中EK代表改進的鏈式受控非加密操作,包含兩步操作：第一步使用受控非操作加密|φ′〉,第二步使用二進制密鑰控制的HadamardH門執行操作,當二進制密鑰為0,H門執行單位矩陣I操作,反之,執行H門操作.EK′代表KCCC加密操作,關鍵點是引進了受控的轉換操作,用以重組簽名態中的量子比特位置,來規避QOTP中一個比特對應一個比特的加密方式引起的可能的抵賴和存在性偽造攻擊[13,18].這個KCCC算法在文獻[18]中已詳細介紹,這里將不再贅述.

4)為了繼續簽名過程,考慮四個頂點的環上的基于兩個硬幣的量子游走模型,其線路原理圖如圖2所示.作用在位置和硬幣空間的條件相移算符Tcircle重寫如下：

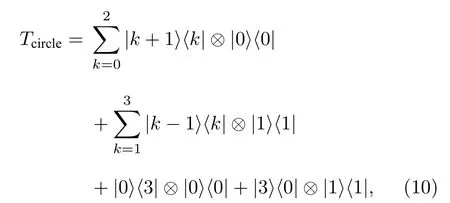
Alice持有兩個粒子A1和A2,硬幣1的態編碼在A1,位置態編碼在A2.Bob擁有一個粒子B,硬幣2的態編碼在B.A1,A2和B的初始態分別為則游走系統的總初始態為

量子游走第一步的幺正演化操作符為

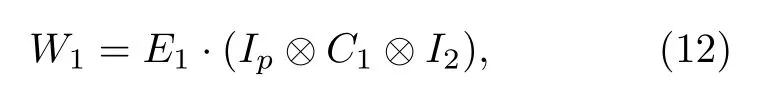
圖2 兩個硬幣的環上的量子游走線路原理圖Fig.2.Circuit diagram of quantum walks on cycles with two coins.

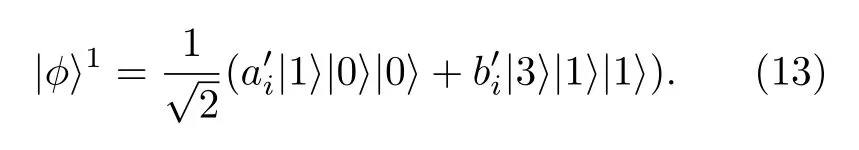
這一步使得位置空間和硬幣空間產生了糾纏,即Alice和Bob之間有了糾纏.量子游走第二步演化算符為

我國職前體育教師在實習階段大多只關注如何組織好體育課堂，鮮有參與其他活動。悉尼大學根據教師的終身專業發展需求，為實習生設定任務，在實習階段要參與一部分班主任工作，契合了其培養全科型教師的目標。目前我國培養中小學教師還是采取明確學科分類的培養方式，教師往往只關注與自身學科相關的教學任務，但目前國內越來越多的中小學要求體育教師承擔“副班主任”工作，這就對職前體育教師的能力提出了新要求。跳出單一學科的限定，豐富實習內容，可以激發職前體育教師突破自身專業限制，對各種影響教學過程的因素給予充分的關注，從不同的視角觀察教育教學問題，促進教師專業化與綜合化的發展，更好地迎合社會需求。

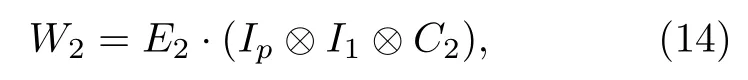
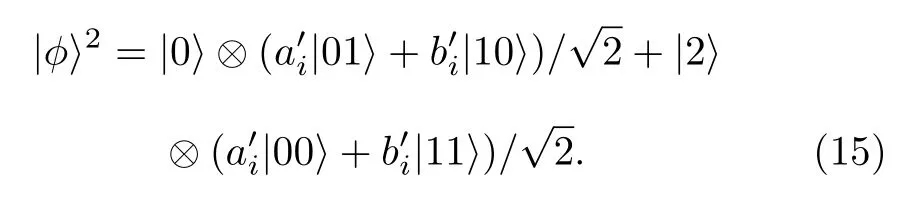
有必要提到的是對于本文系統量子態的表達,其所有的粒子是按照A2,A1與B粒子的順序書寫.

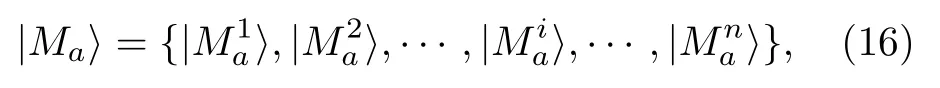
6)Alice 發送|S〉=(|Ma〉,|Sa〉)以 及信息|φ′〉的一個副本給Bob.

3.3 驗證階段

1)Bob通過KCCC加密算法應用密鑰Kb加密得到

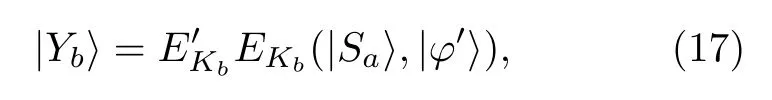
然后Bob傳輸|Yb〉給Charlie.

2)Charlie使用密鑰Kb解密接收到的|Yb〉,得到|Sa〉和|φ′〉.接著 Charlie 用密鑰Ka加密|φ′〉,獲得|Sc〉.為了判斷|Sa〉和|Sc〉是否連續,Charlie設計了驗證參數t,

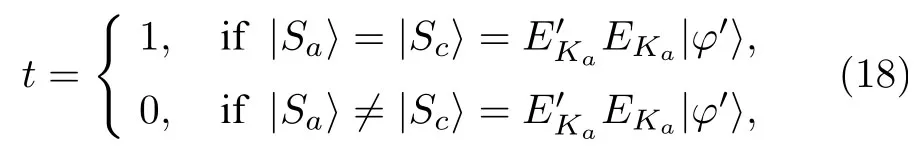
其 中|Sc〉和|Sa〉分 別 從|φ′〉和|Yb〉得到.接著Charlie應用KCCC加密算法使用密鑰Kb加密|Sa〉,|φ′〉和t,生成|Ycb〉,

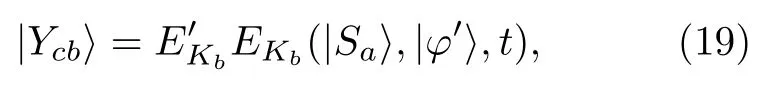
將其傳輸給Bob.

3)Bob使用密鑰Kb解密接收到的|Ycb〉,得到|Sa〉,|φ′〉和t.基于t的值,Bob進行第一輪驗證：如果t=0,簽名也許被偽造,Bob立即拒絕來自Alice的信息|φ〉;如果t=1,它僅僅說明量子態|Sa〉是連續的,需要進行第二輪的驗證.

4)在t=1 的情況下,首先Bob需要恢復出密文信息序列,然后與原密文信息序列|φ′〉進行比較.由于量子游走的第一步之后使得位置空間和硬幣空間之間具有糾纏,Alice對位置和硬幣1的測量使得傳輸的信息坍塌在Bob的硬幣2上.基于Alice的A1和A2的測量結果Ma,Bob執行相應的泡利操作在硬幣2,如表1所列.Bob的測量基表示為

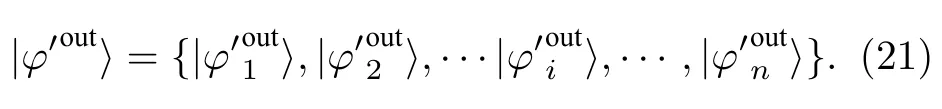
如果|φ′〉/=|φ′out〉,B ob拒絕|φ′〉并放棄這次通信.否則,Bob發布一個請求Alice公布隨機數r的通知.

根據表1,例如,基于Alice的位置和硬幣1的測量結果Ma,Bob可以得到|φ′out〉.其相應的變換規則為：測量結果0與2分別對應于A2的|0〉與|2〉,測量結果1與—1分別對應于A1的|+〉與|-〉.假設Alice應用測量基|2〉在粒子A2,并得到測量結果為2,A1和B之間的糾纏態為

然后當Alice對粒子A1選擇測量基|+〉,即測量結果對應為1,可以看到Bob應用單位矩陣I在硬幣 2 得到,即|φ′out〉=|φ′〉.然而當Alice對A1應用測量基|-〉,Bob得到|φ′out〉為根據表1,Bob應用泡利Z操作在得到變換后結果為即其他兩種情況可以類似的得到驗證.因此,倘若密文信息序列|φ′〉中的n個量子比特都可以得到驗證,那么確定Alice執行的簽名是有效的,密文信息|φ′〉是完整且真實的.

表1 測量結果與對應的恢復操作Table 1.Measurement outcomes and the corresponding recovery operations.

5)Alice通過公共板公布r.

6)Bob使用r從|φ′〉恢復 | φ〉 并確認(|Sa〉,r)為Alice的信息序列|φ〉的簽名.本AQS算法的方案原理圖如圖3所示.

4 安全性分析

首先,我們重述仲裁Charlie在所提出的簽名算法中所起的作用.在初始化階段,Charlie和Alice (Bob)通過量子密鑰分發系統制作準備并分配了秘密鑰Ka(Kb);在驗證階段,Charlie創造了驗證參數t,用以判斷量子態|Sa〉和|Sc〉的連續性,這一步驟有效地輔助Bob完成兩輪的驗證,如步驟3)和4).然后,基于一個簽名算法的安全性規則,我們對提出的簽名算法從不可抵賴、不可偽造與不可否認三個方面給出相應的安全性分析、討論以及與已有典型AQS協議的比較.在這個過程中,我們說Charlie是絕對安全且值得信任的.

4.1 不可抵賴性

Alice不可抵賴自己完成的簽名.從(9)式可以看到,量子態|Sa〉是通過Ka加密|φ′〉得 到,即其中Ka是 Alice和Charlie通過無條件安全的量子密鑰分發系統制備.如果Alice抵賴了|Sa〉并因此與Bob陷入了糾紛,此時通過傳輸|Sa〉給Charlie.如果Charlie判定接收到的|Sa〉中 有Ka,則|Sa〉一定由 Alice 創造;否則,它也許被叛變的Bob或外部攻擊者偽造.

而且,Alice抵賴|Sa〉的概率可以被量化.Alice對|Sa〉有抵賴或接受兩種可能,因此Alice抵賴和接受的概率分別是1/2,將抵賴和接受看作二分變量.假設|Sa〉中的n個量子比特有m個被抵賴,那么Alice抵賴簽名的概率為

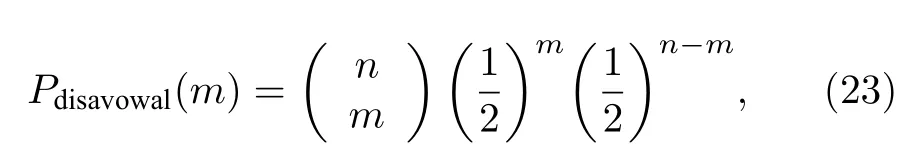
其中

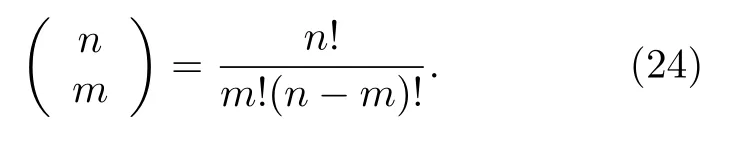
圖3 簽名方案原理圖(QKD代表量子密鑰分發)Fig.3.Schematic of the suggested arbitrated quantum signature scheme.QKD is short for quantum key distribution.

如圖4所示,圖中呈現了n=50,100,150 三種情況,橫軸表示被抵賴的量子比特數m,縱軸為Alice抵賴m個量子比特的概率Pdisavowal(m),可以發現隨著n值變大,抵賴概率的最大值在變小,可以推斷當n非常大時,Alice抵賴的概率可以非常小或接近0.這時假定抵賴概率閾值為Pthreshold,我們規定如果Pdisavowal(m)小 于Pthreshold,認為不存在抵賴行為,否則認為有抵賴行為存在.當n是確定的,抵賴概率閾值可以選擇為抵賴概率的平均值,即

圖4n=50,100,150三種情況下Alice成功抵賴簽名的概率Pdisavowal(m)Fig.4.Alice's disavowal probabilityPdisavowal(m)as a function of the amountmof the disavowed qubit in the signature state|Sa〉for the respectiven=50,n=100 and n=150.

4.2 不可偽造性

任何人無法偽造Alice的簽名量子態|Sa〉.如果Bob是一個叛徒,他想要偽造|Sa〉.假設Bob成功偽造了|Sa〉,那他一定知道了生成|Sa〉的 元素Ka和|φ′〉.然而,獲取這些元素對于Bob來說是不可能的.原因是Ka是Alice和Charlie通過量子密鑰分發系統制備和分配的,它具有無條件安全性,Bob無法獲取Ka,則Bob也就無法成功偽造正確的|Sa〉.不正確的|Sa〉在驗證階段將被Charlie檢測得到t=0 .因此,在Charlie的輔助驗證下,Bob無法偽造正確的|Sa〉.

任何外部的攻擊者也一定是不可能成功偽造簽名|Sa〉的.對于外部攻擊者來說,在本算法中暴露的 參數是|S〉,|Sa〉,|Yb〉和|Ycb〉,它 們 均 通過KCCC[18]加密得到,具有很高的安全性.前面我們已經分析內部參與者Bob是不可能偽造出正確的|Sa〉,且推斷外部的攻擊者也一定是不可能的,也就是說,無條件安全的量子密鑰分發以及高安全性的加密算法確保了本方案的安全性.因此內部參與者和外部潛在的攻擊者都不能成功變造Alice的簽名|Sa〉.

4.3 不可否認性

在提出的AQS算法中,Bob無法否認收到Alice的簽名|Sa〉以 及信息|φ〉,即包含Alice簽名的信息或文件.Charlie的存在使得Bob的否認攻擊策略是不可能的,這種情況和Alice不可抵賴的情況是類似的.即使通過簽名方案減少對Charlie的依賴,這個特性仍然是滿足的.在驗證階段的第一步,Bob傳輸|Yb〉給Alice而不是Charlie.然后Alice實現新的簽名|S′〉,即

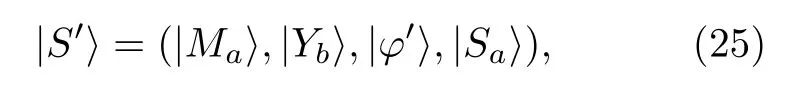
隨后將|S′〉傳送給Charlie.在驗證階段的第二步Charlie制備新的|Ycb〉,即

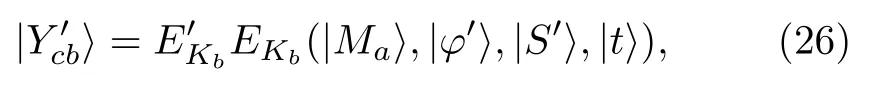
這時可以看到|S′〉包 含Alice的密鑰Ka和Bob的密鑰Kb.一旦Bob想要否認,Charlie如果檢測到|S′〉中 包含Kb,則Bob一定接收到了包含Alice簽名的文件或信息.因此Bob是不可能成功否認接收到的Alice的文件或消息.

4.4 討 論

根據Gao等[13]對AQS算法的密碼學分析,討論本方案是否可抵抗Alice的抵賴攻擊以及Bob的存在性偽造攻擊.例如在驗證階段的第二步,在Charlie完成判斷之后,Charlie傳輸給Bob.此時,Alice有時機去修改簽名態|Sa〉產 生使得它不再是信息序列|φ〉的有效簽名.由于所使用的KCCC算法的特點,這種修改是無法成功的,Alice不再像QOTP算法中一樣可以準確獲取簽名量子態中量子比特的位置和順序.因此,KCCC算法在AQS中的使用可以規避此類攻擊.

此外,Bob也是無法成功實現已知有效的簽名信息對下的存在性偽造攻擊.這種攻擊是假如Bob擁有一個有效的信息簽名對 (|φ〉,|Sa〉),他執行n次泡利操作(I,X,Y,Z)在|φ〉中的量子比特,同時相同的操作執行在|Sa〉的后n個量子比特,得到的新的信息簽名對稱為是一個成功的偽造,其中每一個泡利操作是四個泡利操作I,X,Y,Z之一,Bob至少可以實現 4n-1 種偽造,他可以選擇對自己利益最大化的信息聲稱是Alice簽的.這時Charlie總會站在Bob這邊.然而由于KCCC加密算法的應用,這種攻擊是不可能的.首先需要明確的是在Bob接收Alice的簽名之前是不可能的,原因是信息序列是以密文|φ′〉的形式存在,在完成驗證之后,Bob才可以通過公布的隨機數獲取原始信息序列|φ〉.在驗證階段之后,仍然是不可能的,因為Bob無法準確獲取簽名態中量子比特的準確位置和順序,則Bob無法執行等效的操作在有效的信息簽名對,無法成功獲取簽名|Sa〉的偽造.

4.5 比 較

基于量子游走隱形傳輸模型、KCCC操作、隨機數以及公共板的應用,本文提出了一種目前較好的一種AQS方案.我們將其與已存在的幾種典型的AQS協議進行比較,如表2所列：根據所使用的量子資源、信息副本的傳輸方式、加解密操作、Alice的抵賴攻擊是否成功以及Bob的存在性偽造攻擊是否成功進行對比.可以看到信息副本的傳輸方式分為三種：基于糾纏態的隱形傳輸[2,11,14,16],普通量子加密方式[12]以及本協議的基于量子游走不需要提前準備糾纏態的隱形傳輸方式.對于采用QOTP算法或者改進的QOTP的AQS協議,均不能抵抗Alice的抵賴攻擊和Bob的存在性偽造攻擊,這個現象在文獻[13]中已做了分析,他們展示抵賴或偽造攻擊成功的原因是QOTP加密的方式是一個比特對應一個比特,量子比特的位置和順序在基于QOTP的AQS協議中是確定的,攻擊者可以找到相應的量子比特位置并執行泡利操作對其修改.文獻[16]中提出的采用受控非代替QOTP,仍然不能抵抗Bob的偽造攻擊[18],幸運的是受控非修改了量子簽名中的量子比特使其之間互相關聯,可以有效防止Alice的抵賴攻擊.本方案使用Zhang等[18]提出的KCCC操作作為中間量子態傳輸的加解密方法,使用量子游走隱形傳輸模型[25,26]傳輸信息副本,本協議具有文獻[18]的所有優勢.此外,相比于普通的量子加密方式,基于量子游走的隱形傳輸具有如下優勢：第一,不需要傳輸載體粒子本身,傳輸的是粒子所處的量子狀態;第二,沒有物理限制,便于擴展傳輸距離,量子加密僅限在地區性的網絡上,量子中繼器還不存在;第三,由于糾纏的存在在傳輸過程中具有防竊聽功能,即一旦有竊聽者想要竊聽信息,測量引起的擾動會被誠實的參與者發現.相比于普通的量子隱形傳輸,基于量子游走的隱形傳輸不需要提前制備糾纏態,必要的糾纏態可以在量子游走的第一步自動產生.此外,從通信效率來說,相比于典型的文獻[2]和文獻[11],本方案的驗證階段的第一步不需要傳輸測量基Mb,所以本方案的通信效率更高,通信負擔更小.因此,本AQS方案目前來講是較優的.

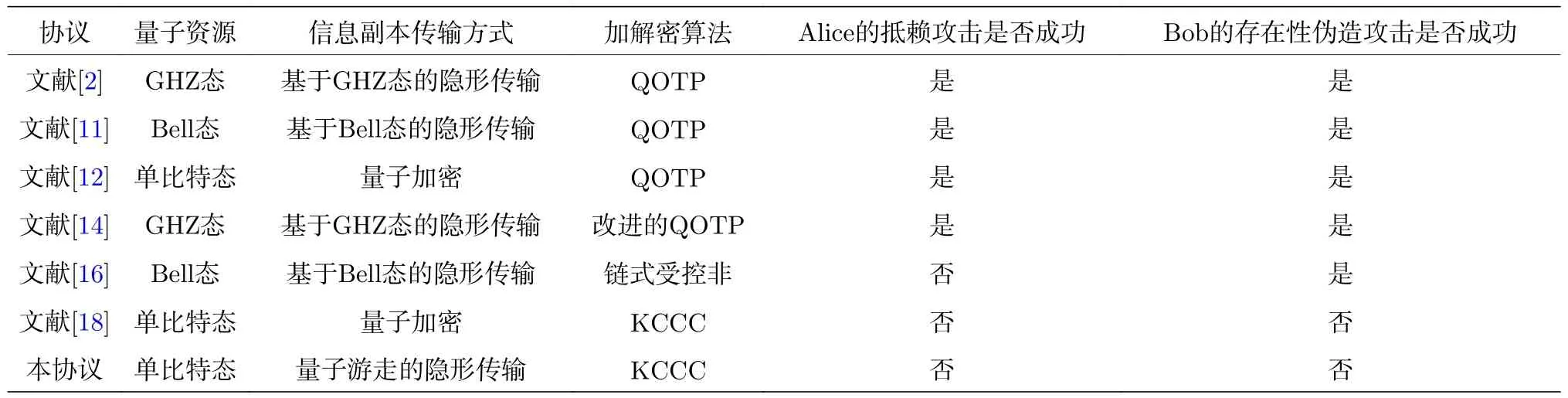
表2 協議比較Table 2.Protocols comparison.

5 結 論

本文設計了基于環上兩個硬幣的量子游走的AQS算法.不同于已有的AQS協議,在初始化階段不需要制備糾纏態,而是在簽名階段量子游走的第一步產生Alice和Bob之間的糾纏態.基于量子游走的量子隱形傳輸模型,兩步游走之后,Alice應用測量基|0〉,|2〉和|+〉,|-〉在自己的量子態,由于Alice和Bob之間糾纏的存在,Alice的測量使得傳輸信息塌陷在Bob的量子態.Bob執行相應的泡利操作恢復信息,進而驗證簽名的有效性以及信息的完整性和真實性.由于KCCC算法的使用,本算法滿足簽名方案的安全性規則.目前,Xue等[32]在實驗上已成功證實了量子游走可以應用于量子通信,且量子游走在一維空間已經做到20步以上.所以,基于當前的技術,實現本文提出的AQS協議是切實可行的.