知識圖譜復雜網絡特性的實證研究與分析*

丁連紅 孫斌 時鵬

1)(北京物資學院信息學院,北京 101149)

2)(北京科技大學國家材料服役安全科學中心,北京 100083)

1 引 言

復雜網絡理論興起于20世紀90年代,是對復雜系統的一種抽象和描述方式.復雜網絡由節點和邊組成,節點表示元素,邊表示元素之間的互相作用.復雜網絡普遍存在于現實世界,如生物分子網、互聯網、交通網、電力網等.

知識圖譜由Google公司于2012年提出后,就在搜索引擎與人工智能領域備受關注.知識圖譜旨在通過語義知識的結構化儲備實現智能檢索、自動問答等應用,相關研究主要圍繞著知識圖譜的知識提取、知識融合以及知識推理等進行.知識圖譜描述知識之間的語義關聯,同樣可以網絡化.網絡化的知識圖譜是否符合復雜網絡模型？知識間的關系是否可以通過復雜網絡理論進行分析？目前尚沒有明確的結論.微軟概念圖譜(Microsoft concept graph)是微軟研究院于2016年發布的一個知識圖譜,其形式為概念(concept)、實例(instance)和關系(relation)的三元組,描述實例與概念之間的IsA關系,用于實現實例的概念化推理[1].例如三元組(sport,basketball,6423)表示basketball與sport之間存在IsA關系,即basketball是一種sport.其中basketball (籃球)是實例,sport (運動)是概念,6423是從微軟bing搜索日志中抽取到的basketball和sport之間的IsA關系的次數,以下稱為共現次數.概念和實例是對事物的描述,概念較抽象,通常描述事物的類別,例如fruit (水果);實例描述較為具體,一般為具體事物的名稱或標識,例如orange (橙子).概念圖譜正是通過這些由用戶搜索記錄提取到的實例、概念以及它們之間的IsA關系反映人們對實物的認知和理解.

本文以微軟概念圖譜為研究對象,構建描述概念與實例之間概念化關系的概念圖譜網絡,進而研究概念詞與實例詞之間的關聯關系.選取該研究對象的優勢在于：1)圖譜數據來源于bing搜索日志中數以億計的用戶搜索記錄,反映了用戶對事物的真實看法;2)圖譜中的共現次數反映了IsA關系的可信度,可據此調整網絡規模;3)微軟概念圖譜只有IsA一種關系,在構造網絡時不需要對關系進行區分,簡化了網絡模型的構建.

首先采用NetworkX工具計算相關統計特征[2],但由于概念圖譜網絡的節點數量巨大,導致計算時間過長,因此本文提出一種適用于概念圖譜的子網提取算法,用來獲取最大連通子網,在時間和空間效率上都有顯著提高,并對最大子網的復雜網絡特征進行了分析.在計算網絡的最短平均路徑長度時,本文提出了一種計算概念圖譜網絡近似平均最短路徑的方法,并對算法準確性進行了驗證.對于聚類系數的計算,本文根據節點度值給出了不同的聚類系數求解方法,并采用Map/Reduce模式進行了計算提速.

2 相關工作

復雜網絡理論起步于Erdos和Renyi的隨機圖論(ER圖),而后隨著Watts和Strogatz[3]提出的小世界網絡、Barabási和Albert[4]提出的無標度網絡逐漸興起,復雜網絡理論為復雜系統的特征分析提供了重要的理論依據,已被廣泛應用于社會網絡分析[5]、城市建設用地布局[6]、國際貿易交流分析[7]、交通運輸分析[8]等.其中交通運輸領域的應用又包括公路交通[9]、軌道交通[10]、鐵路[11]、航運[12]、航空[13]等.通過求解網絡特征,如網絡節點的度分布、平均路徑長度、聚集特性以及介數中心性等,分析復雜系統中各因子之間的關系和整體穩定性[14].以上文獻中復雜網絡系統的節點以交通站點、城市、國家等為主,邊以交通線路、城市區域間道路、國家關系等為主,系統中節點和邊的數量較少,且多為連通網絡,因此分析其統計特性時資源消耗不大.

在研究如萬維網[15,16]、電話呼叫網[17,18]這類超大規模網絡時,由于很難得到描述整個網絡結構的全部信息,通常的方法是先分析局部實際數據的特性,根據這些特性建立實際網絡的數學模型,再由數學模型推算整個網絡的相關特性.Albert等[16]先從萬維網抓取了部分實際數據,得到其局部結構,據此分析出節點的度分布符合冪律分布,并根據擬合結果對局部網絡進行擴展得到較大規模的拓撲結構;據此分析萬維網的拓撲結構和連接特性,得到網絡半徑與節點數量之間的函數關系;最后,將萬維網節點實際數量代入該函數推測出萬維網的網絡直徑.Aiello等[17,18]也通過類似的方法對電話呼叫網進行了拓撲建模和演化研究.目前較快的串行最短路徑算法的時間復雜度也只能降低到O(n2.376)[19],n為網絡節點的數量.

隨著時間的發展,萬維網的節點數量早已超過數十億數量級,邊的數量更是不計其數;電話呼叫網絡根據已存在的電話線路之間的關系進行建立,包括約47000000個節點,80000000條邊.對于規模如此巨大的網絡直接計算其直徑(節點間最短路徑的平均值)和聚類系數幾乎是不可行的.這可能是相關文獻均未給出具體的網絡聚類系數值,對于網絡直徑也只給出由網絡模型計算得到的推測值的原因[15,17,18].

因此有學者開展了網絡精簡、評估方法改進、網絡結構優化等研究.網絡精簡通過閾值網絡[20]、最小生成樹[21]、差分網絡[22]等方法減小網絡的規模.孫延風和王朝勇[23]采用互信息表示金融網絡中節點間的關系,并用閾值網絡和最小生成樹對網絡進行精簡,最后驗證了網絡模型的有效性.

評估方法改進包括基于度中心性的評估方法[24]、k-shell分解[25]和基于PageRank的評估方法[26]等.Ruan等[27]將約束系數引入節點核心性的度量,提出了一種綜合節點鄰居節點的k-shell值和鄰居節點間拓撲結構的核心性度量方法,該方法能更準確地評估節點的傳播能力.孔江濤等[28]利用復雜網絡動力學模型描述復雜網絡中節點間的相互影響活動,建立了基于偏離均值與偏離均值的方差的兩級節點重要性評估標準,并通過擾動測試和破壞測試驗證了標準的有效性.

網絡結構優化主要以實際應用為目的,如韓定定等[29]結合時變特征和網絡客流分布,對航空網進行優化,提出了一種快速推算航線網絡最優拓撲及相應航班頻率分布的方法.Niu和Pan[30]通過自組織優化機制對運輸網絡進行優化,證明了無標度網絡在gradient-driven運輸模式下可以有效地通過自組織優化機制提高運輸能力.Jiang等[31]以中國航空運輸網(CNTA)為例研究多層網絡融合過程的本質,通過一系列拓撲屬性刻畫多層網絡的融合過程,發現CNTA在融合過程中發生了明顯的結構轉換,為中國航空運輸系統的網絡結構優化和管理提供了啟示.

而知識圖譜作為智能化的語義知識儲備,其規模也會隨著時間而不斷積累擴大,節點數量往往突破千萬數量級,對這類大規模網絡的特征計算也必然十分復雜與耗時.NetworkX是一款用Python語言開發的復雜網絡構建與分析軟件工具包,是復雜網絡建模與分析的有力工具[2].由于知識圖譜的規模巨大,使用NetworkX僅是構建出整個網絡便需要消耗近40 GB的內存.萬維網可以通過網絡中的路由設備找到通往各個網站節點需要跳轉的次數,即平均最短路徑長度,而知識圖譜與萬維網不同,知識間的拓撲距離無法如此計算.為了解決大規模復雜網絡分析的問題,有學者設計了近似算法以計算復雜網絡的平均距離.Rattigan等[19]通過引入網絡結構索引(network structure index,NSI)計算節點間路徑,從而降低計算網絡平均路徑長度這樣的基于節點間路徑應用的搜索復雜度.NSI由各個節點的標記和根據節點標記估算節點對間距離的函數構成.唐晉韜等[32]提出了基于區域中心點距離(centers distance of zone,CDZ)的復雜網絡最短路徑計算的近似方法,根據網絡特征將網絡分成多個區域,每個區域都設置一個中心點,將兩節點之間的距離轉換為節點到中心點以及中心點間的距離之和,實現近似計算.受CDZ思想的啟發本文提出了一種根據節點所在網絡層與中心節點的距離及不同網絡層之間的距離計算概念圖譜網絡近似平均最短路徑的方法.

3 概念圖譜網絡構建及最大連通子網抽取

3.1 概念圖譜網絡構建

微軟官方提供的概念圖譜的數據文件是一個純文本文件,構成該文件的元數據是描述實例與概念之間IsA關系的三元組.通過對該數據文件的遍歷發現,有些詞既作為概念(Concept)出現,也作為實例(Instance)出現,本文將這部分詞稱為子概念詞(subConcept).為了構建描述實例與概念之間的實例關系的復雜網絡,將概念、子概念和實例作為網絡的節點,在存在IsA關系的兩個節點之間添加一無向條邊,表示它們之間的實例關聯,從而構建出如圖1所示的描述概念、子概念、實例之間的實例關聯的概念圖譜網絡.

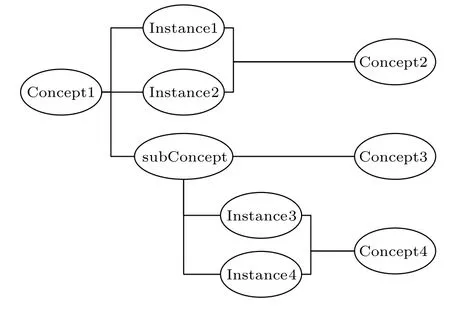
圖1 概念圖譜網絡示意圖Fig.1.Network of concept graph.

建立的概念圖譜網絡是一種無向非加權網,具有如下特征：1)網絡規模巨大,包括16936670個節點和33354328條邊,因此建立非加權網絡以減少計算復雜度,便于特征分析;2)只描述概念和實例間的IsA關聯及關聯間的跳轉層次,忽略關系的方向;3)共現次數描述節點間關系的可信度,旨在通過閾值設置得到不同較小規模的概念圖譜網絡以進行深入的比較分析.

表1列出了在整體概念圖譜網絡中,概念詞、實例詞以及子概念詞的度值分布.在概念圖譜網絡中,概念節點的度表示有多少個實例或子概念與該概念存在IsA關系.實例節點的度表示該實例與多少個概念或子概念具有IsA關系.首先,因為概念圖譜的基本數據是由概念、實例和它們之間的IsA關聯構成的三元組,因此,每個概念至少與一個實例相關,一個實例也至少與一個概念相關,因此所構建的概念圖譜網絡中不應有孤立節點,即不存在度為0的節點,這與表1的統計數據一致.其次,由于子概念既可以處在概念的位置,也可以處在實例的位置,所以子概念的度都應大于等于2.但由表1可知概念圖譜網絡中有18個子概念節點的度為1.為探究該現象,在概念圖譜的數據文件中對度為1的子概念節點進行了檢索和分析,發現存在類似于(small business issuer,company,4)和(company,small business issuer,1)這樣的兩個節點互為對方的概念與實例的情況.同時,因為這兩個節點都未出現在其他三元組中,所以它們的度都為1.這些度為1的子概念節點也揭示了所構建的概念圖譜網絡并非一個連通網絡.因此,為了真實描述其網絡特性,必須抽取該網絡的最大連通子網,并將其作為后續研究對象分析概念圖譜網絡的復雜網絡特性.

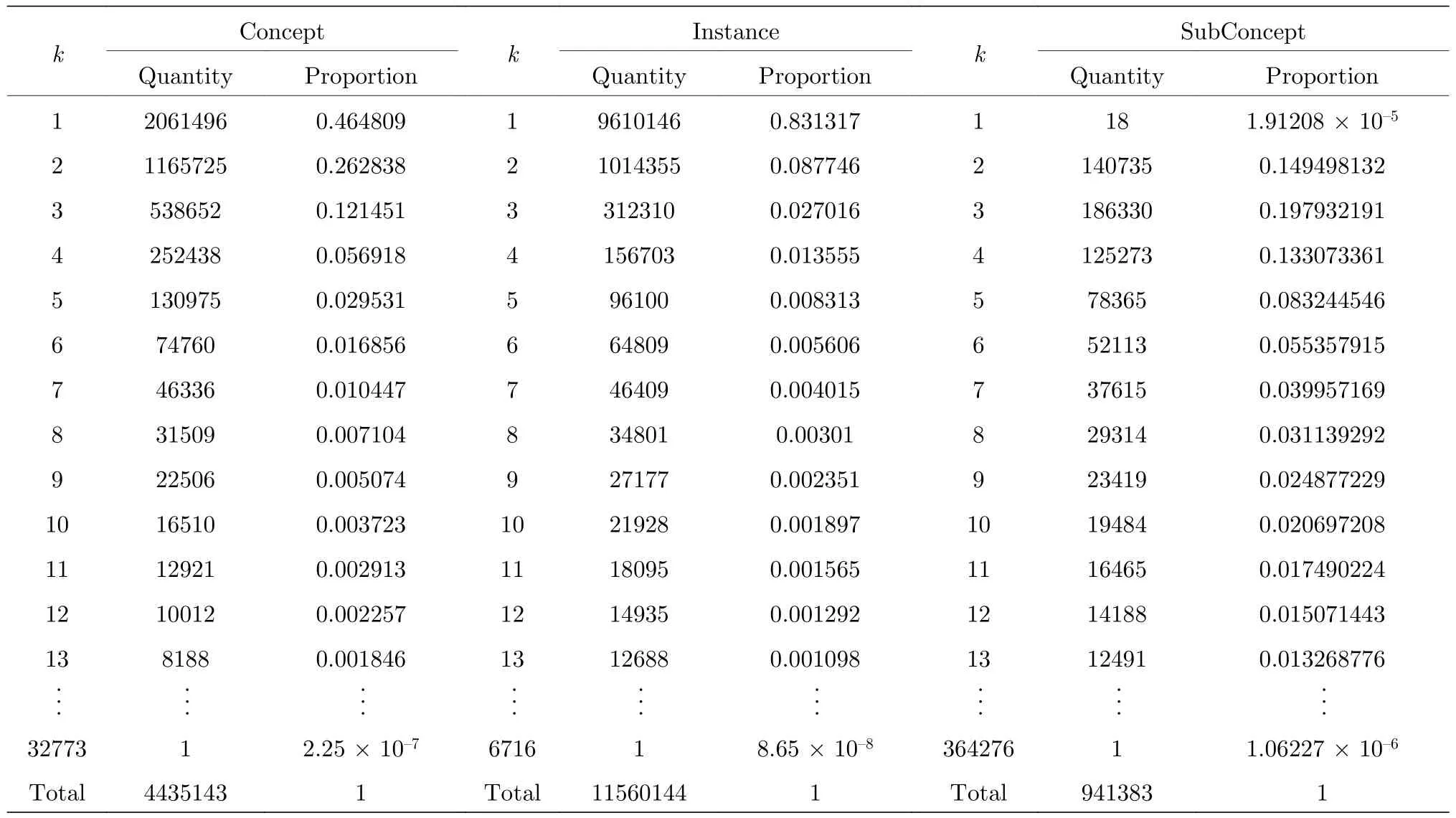
表1 概念圖譜網絡的節點度分布Table 1.Degree distribution of the concept graph network.

3.2 子網抽取算法

由于概念圖譜網絡不是連通網絡,無法計算節點間的平均距離,所以需要計算出概念圖譜網絡的最大連通子網.我們按照廣度優先思想,實現了基于廣度優先的子網提取算法(SubNet Extraction based on Breadth-first,SNEBF).

算法1基于廣度優先的子網提取算法(SNEBF)

輸入：概念圖譜數據文件Graph

輸出：最大連通子網節點集合MaxSubNet

1)從Graph中抽取一個三元組,該三元組包含的兩個節點的度之和最大,將該三元組中的概念和實例作為兩個初始節點,構成初始節點集合InitialSet,并將這兩個節點加入MaxSubNet.

2)對InitialSet中的每一個節點node

{a.遍歷Graph中的三元組(概念(con),實例(ins),關系(rel))信息,如果其con或ins等于node,則將該三元組中相應的ins或con加入節點node的鄰居節點集合NeighborSet.

b.判斷NeighborSet中是否還有未加入MaxSubNet的節點,如果有,將這些節點加入MaxSubNet,將NeighborSet集合與MaxSubNet的差集并入InitialSet.}.

3)返回MaxSubNet.

類似于廣度優先的按層掃描,對于InitialSet中的每一節點node算法1總是找出其全部相鄰節點并據此對最大子網進行擴展,對找出的相鄰節點重復相同的操作.但在實際運行時,由于網絡中的節點之間關系復雜,不同節點的鄰居節點集合可能相互包含了許多相同的節點.如在圖2所示的概念圖譜網絡中,Concept1的鄰居節點集合包括4個節點：Instance2,Instance3,Instance4和Instance5.Concept2也有4個鄰居節點：Instance1,Instance2,Instance3和Instance4.其中Instance2,Instance3和Instance4是Concept1的鄰居節點也是Concept2的鄰居節點.

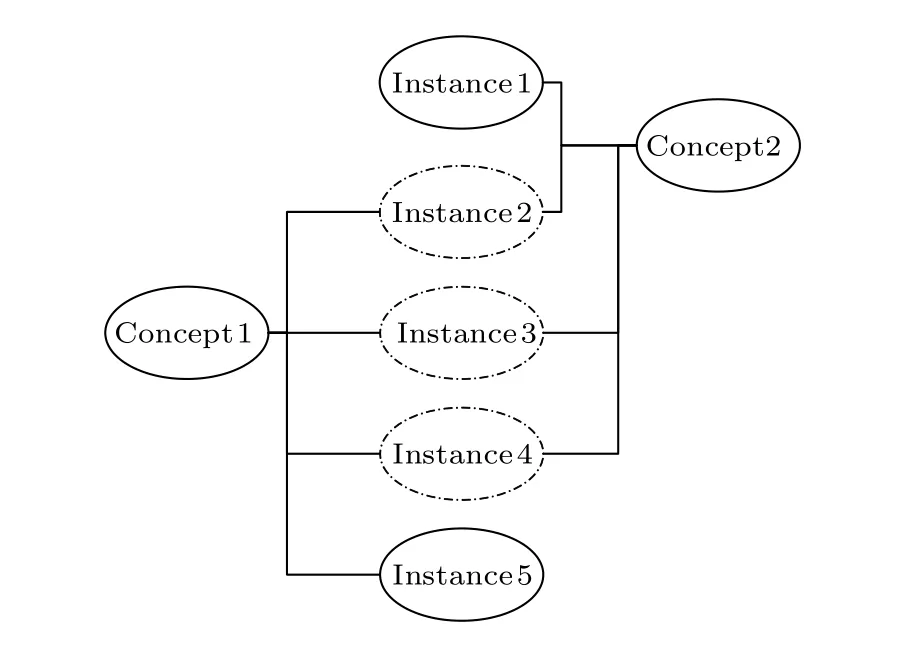
圖2 導致節點的鄰居節點集合冗余的網絡結構Fig.2.Network structure leading to the overlap of neighbor node sets.

這些相同的節點在處理Concept1的鄰居節點和Concept2的鄰居節點時會被重復進行遞歸檢索處理.這不但會增加大量的冗余存儲空間而且需要多次重復檢索圖譜數據.同時由于算法中循環嵌套了循環,所以在進行遍歷時十分耗時.因此我們引入集合運算,從而得到基于集合運算的子網抽取算法(SubNet Extraction based on Set Operation,SNESO).

算法2基于集合運算的子網抽取算法(SNESO)

輸入：概念圖譜數據文件Graph

輸出：最大連通子網節點集合MaxSubNet

1)從Graph中抽取一條包含度值最大節點的三元組信息,將該三元組中的概念和實例作為中心節點構成最大連通子網的中心層SubNeti(此時i=1),并將其加入MaxSubNet.

2)尋找SubNeti集合的鄰居節點,即遍歷Graph中的(con,ins,rel)信息,判斷其con或ins是否屬于SubNeti集合,若存在,則表示對應的ins或con是集合SubNeti的鄰居節點,將這些節點加入SubNeti的鄰居節點集合NeighborsSeti.

3)判斷NeighborsSeti中是否還有新的未在MaxSubNet中的節點,如果有,則將NeighborsSeti并入MaxSubNet,將SubNeti替換為NeighborsSeti與MaxSubNet的差集,i=i+1.然后跳轉至步驟2;若無,則繼續步驟4.

4)返回MaxSubNet.

算法1和算法2的關鍵操作是對Graph三元組信息的遍歷.由中心層出發,每掃描一次Graph,算法1獲得一個節點的鄰接節點,算法2獲得一層節點的全部鄰接節點,因此算法2能顯著減少對Graph的掃描次數.由于度值大的節點在最大連通子網的概率較高,為了保證可以找到最大子網,我們從度值最大的節點以及與最大節點相連的度值較大的節點開始進行搜索.在實際運行中,運算時間和空間復雜度確實有所降低,具體的復雜度分析見3.3節.

先由算法2得到最大連通子網的節點集合MaxSubNet;再根據MaxSubNet從概念圖譜數據文件Graph中提取出最大子網的邊的集合,其中的每條邊依然采用Graph中的三元組形式并存儲在文本文件GraphLink中;最后由MaxSubNet和GraphLink生成如圖3所示結構的最大連通子網.其中,中心層(Central Layer)由兩個節點構成,這兩個節點是各三元組對應的節點對中度值和最大的節點對;第二層(Layer-2)為中心層各節點的鄰居節點的集合;第三層(Layer-3)為第二層的各節點的鄰居節點的集合.以此類推,直到網絡的最外層(Outermost Layer).

圖3 最大連通子網的分層邏輯結構Fig.3.Hierarchical logical structure of the largest connected subnet.

3.3 算法復雜度分析

根據算法1我們實現了函數GetNeighbor(Node,Graph),該函數遍歷Graph中的邊(三元組)信息,判斷Node是否為當前邊的端點.由于一條邊有兩個端點,完成一條邊的掃描需要兩次判斷操作.將1個端點的判斷操作定義為1次基本操作,Graph的邊數為n,則GetNeighbor(Node,Graph)的時間復雜度為2n.由算法1可知,每當最大連通子網中有一個新的節點,就要調用一次GetNeighbor(Node,Graph).設最大連通子網的節點數為m,則算法1的時間復雜度為m×2n.由后面3.4節的實際計算結果可知,m近似為n/2,所以算法1的時間復雜度為O(n2).

算法2在算法1的基礎上引入了集合運算,兩者的區別在于：算法1每遍歷一次Graph可以找出一個節點的鄰居節點;算法2每遍歷一次Graph可以找出一層節點的全部鄰居節點,只要將函數GetNeighbor的參數由Node改為NodeSet即可.該函數遍歷Graph中的邊信息,判斷邊端點是否在集合NodeSet中.由于GetNeighbor(Node,Graph)的時間復雜度為2n,由3.4節的實驗可知GetNeighbor(NodeSet,Graph)的平均運算時間約為算法1中GetNeighbor(Node,Graph)運行時間的1.6倍,所以GetNeighbor(NodeSet,Graph)的時間復雜度為1.6×2n=3.2n.由算法2可知,對最大子網的每一子網層需調用一次GetNeighbor(NodeSet,Graph),設構建最大連通子網過程中,子網層數為nl,則運行GetNeighbor(NodeSet,Graph)的次數為nl次,所以算法2的時間復雜度為nl×3.2n.通過3.4節的最大子網抽取實驗發現,nl的實際值為12,由于nl遠小于n(33377320),所以算法2的時間復雜度近似為O(n).

3.4 最大子網抽取實驗與對比

分別采用NetwrokX和算法1(SNEBF)、算法2(SNESO)對所構建的概念圖譜網絡進行了最大連通子網的抽取實驗,具體的實驗環境為64位Win7系統,16 GB內存,Anacodna集成Python開發環境,其時間復雜度和實際運算時間見表2.

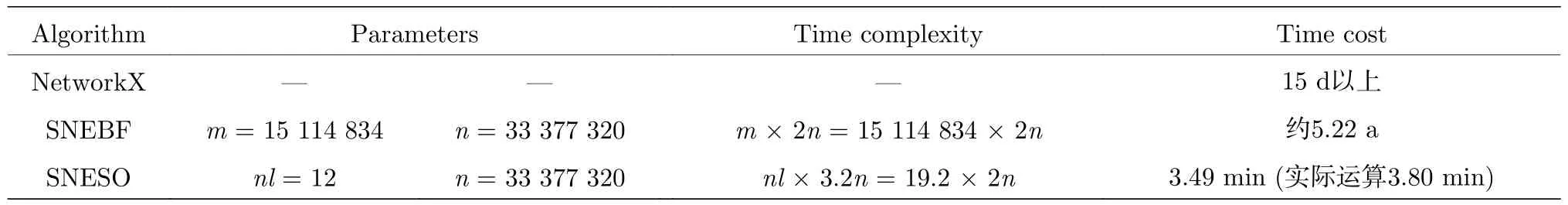
表2 最大子網提取算法時間復雜度對比表Table 2.Time complexity of the subset extraction algorithms.

其中采用NetworkX以及SNEBF求解最大子網時程序并未運行出結果,在實際運行時間為15 d時終止了這兩個程序,由此可以得出NetworkX構建最大子網時間大于15 d的結論.實驗過程中SNEBF中的GetNeighbor (Node,Graph)運算時間約為10.9 s,SNESO中的GetNeighbor (NodeSet,Graph)的平均運算時間為17.6 s,約為GetNeighbor(Node,Graph)的1.6倍.因為SNEBF的時間復雜度為(m×2n),而2n,即GetNeighbor(Node,Graph)的平均運行時間為10.9 s,所以可以推算出SNEBF的運行時間約為m×2n=15114834×10.9 s=5.22 a.由GetNeighbor(NodeSet,Graph)的平均計算時間和nl=12,得到SNESO的運行時間為3.49 min,而該算法的實際運行時間為3.80 min.所以,SNESO時間復雜度最小,計算速度最快,運算時間在可接受范圍內,遠小于SNEBF的運行時間.

使用NetworkX抽取最大子網,首先通過其內部函數connected_component_subgraphs(Graph)求解所有子網[33],再從中找到節點數量最多的子網,即為最大連通子網.connected_component_subgraphs(Graph)的輸入是一個無向NetworkX圖G,輸出是G的所有連通子網的列表.該函數是一個由兩行代碼構成的for循環：

forcin connected_components(G)：

yieldG.subgraph(c).copy()

其中connected_components(G)返回各個連通子網的全部節點c的列表,G.subgraph(c).copy()將節點列表c轉換成圖G的一個連通子圖.以下是connected_components(G)的定義：

① seen={};

② forvinG：/*對G中的每個節點v*/

③ ifvnot in seen：/*如果沒有遍歷過節點v*/

④c=sp_length(G,v);/*計算點v到所有可以連通節點的距離字典c*/

⑤ yield list(c);/*將獲得的c轉換為列表返回*/

表3 算法空間復雜度和實際內存消耗對比表Table 3.Space complexity of the algorithms.

⑥ seen.update(c);/*更新seen的值以確保不會尋找重復節點*/

⑦ end if

⑧ end for;

NetworkX求解最大子網的關鍵操作是sp_length(G,v)函數,具體的時間復雜度分析在第4節中采用事后統計法給出.

表3列出了NetworkX與算法2運行時的實際內存消耗.實驗中NetworkX抽取概念圖譜最大連通子網至少需要40 GB內存.采用SNESO求解最大子網時,占用內存的變量為SubNeti,NeighborsSet,MaxSubNet,數值與最大子網的節點數、子網某層的節點數相關,實際占用內存為5.23 GB.

由算法2根據概念圖譜的數據文件生成的最大子網包含15114834個節點和32274081條邊,分別占整個概念圖譜網絡節點和邊的89.24%和96.69%.可知該子網覆蓋了概念圖譜網絡絕大部分的節點與邊,其網絡特性可以較好地反映出整個網絡的特征,后續對概念圖譜復雜網絡特性的分析都基于此最大連通子網.

4 概念圖譜網絡的復雜網絡特性分析

復雜網絡的統計特征主要包括度分布、kshell核心性、平均路徑、聚類系數和度相關性等.

1)度分布p(k)：度分布可以用來表征網絡最基本的拓撲特性.圖4是最大連通子網的節點累積度分布,節點度呈冪律分布,符合無標度網絡特性.

表4統計了三類節點中度值為1—13的節點數量與比例：82%的實例節點度值為1,即82%的實例只與一個概念相關.度值為1的節點,實例占85.5%,概念占14.5%.由此判斷在自然語言處理過程中使用實例詞比使用概念詞更不易因一詞多義而引起文本描述的歧義.82%的概念度值在1—3之間,表明絕多數概念只有1—3個含義.在度值相同的節點中,子概念的比例隨度值的增大而增加,表明子概念通常作為連接多個節點的核心節點.

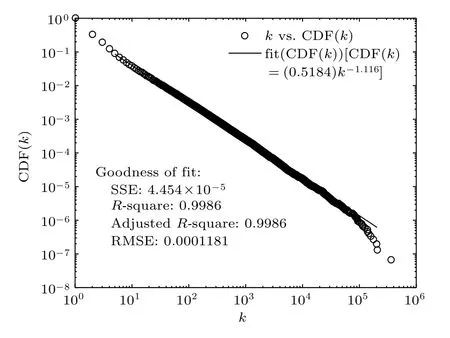
圖4 概念圖譜最大連通子網累積度分布Fig.4.Cumulative degree distribution of the largest connected subnet.

2)k-shell核心性：思想是處于網絡核心位置的節點,即使度很小,對網絡的影響力也可以很大.k-shell分解把網絡由邊緣至中心劃分成若干層,能夠有效識別網絡核心.

概念圖譜最大子網經k-shell分解為185層,圖5是各層節點的度分布及平均度值,可見節點度越大其k-shell分層越高,越靠近中心層,說明大度值節點位于靠近概念圖譜網絡中心的位置,而不是邊緣位置.如圖5所示,度高于10000的節點大都劃分到了核心層,只有極少數k-shell值很低.我們發現這些節點的多數鄰居節點的度很低.如劃分到13-shell層的節點“common search term”和“connected tool”的度高達102033和31963,但這兩個節點的鄰居節點中度為1的分別多達101892個和31942個.

核心層(185-shell)包括786個節點,其中子概念782個,概念和實例各2個.核心層節點間有119162條邊,構成了一個稠密圖,網絡密度0.386,遠高于最大子網的2.825×10—7.表5是核心層中度值最高的20個節點及其度值.

雖然子概念只占最大子網節點的6.2%,卻占核心層的99.5%.說明子概念在概念圖譜中起著重要的連接作用.其根源在于子概念既可以作為比其描述能力抽象的詞的實例,也可以作為比其描述具體的詞的概念,如topic作為概念時包括cultural,political,physica等實例,這些實例都可以說是某一種具體的topic (話題),都與topic具有IsA關系.作為實例時,topic又是多個概念的實例,如concept,document,information等.

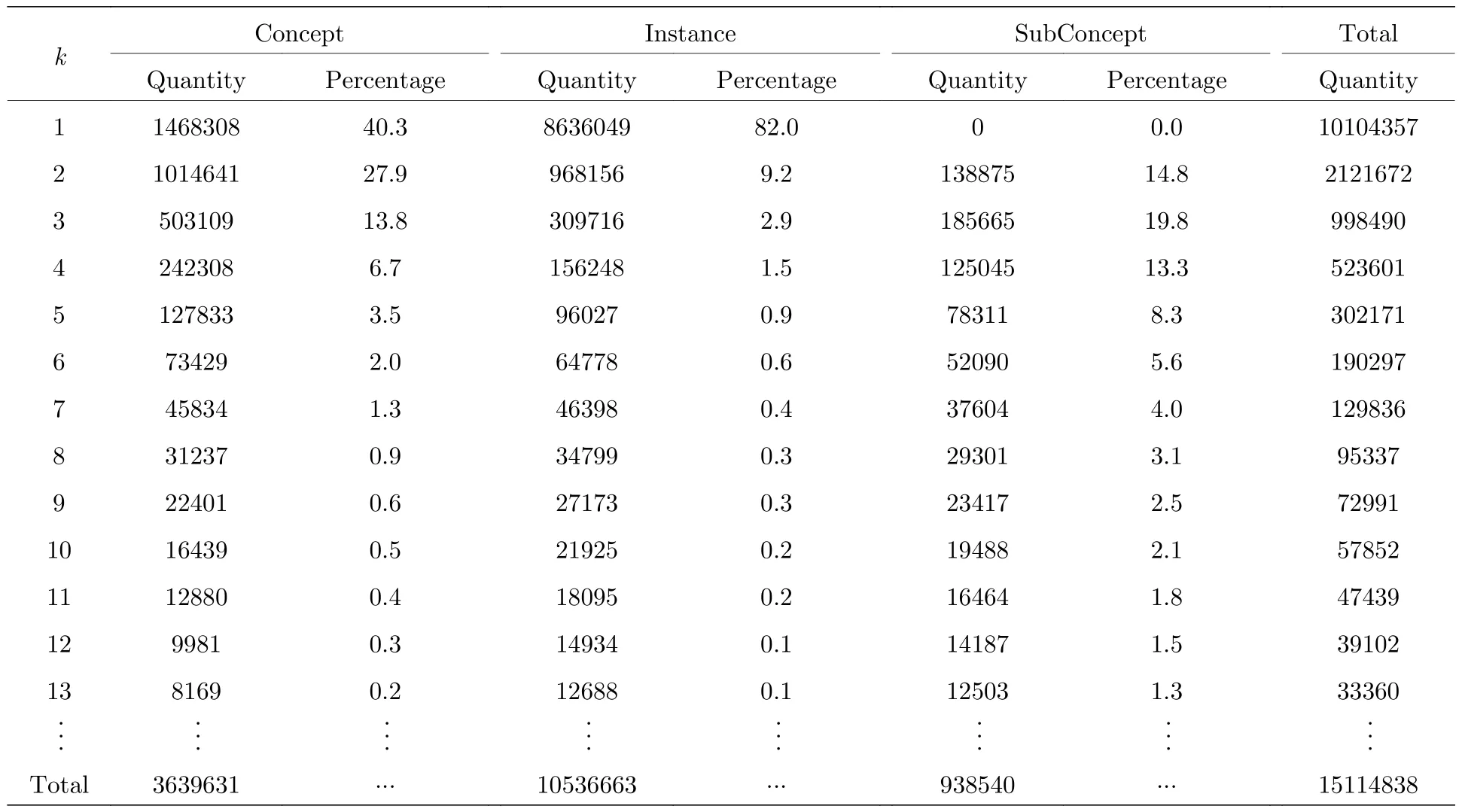
表4 概念圖譜最大子網度分布分析Table 4.Degree distribution analysis of the largest connected subnet.

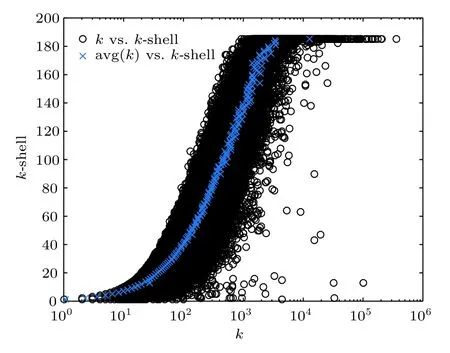
圖5 節點度與k-shell分解中心性關系Fig.5.Relationship between degree andk-shell.

3)平均路徑：網絡的平均路徑avg(l)是所有節點對之間距離的平均值,它描述了網絡中節點間的分離程度.目前最快的串行最短路徑算法只能將計算的時間復雜度降到O(n2.376)[19].概念圖譜網絡的節點數為15114834,要精確計算平均最短路徑,需要計算114229095866361個節點對之間的最短路徑,計算量巨大;同時計算過程中每條路徑上需要存儲多個節點信息,存儲消耗也很大.

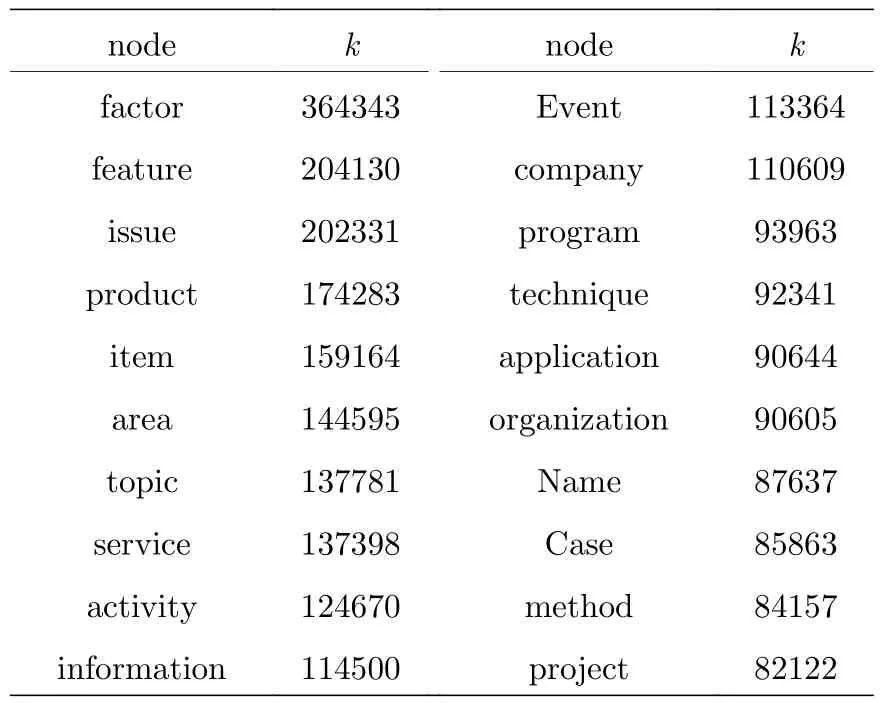
表5 核心層中度值最高的20個節點Table 5.Top 20 nodes with the highest degree in core.

首先嘗試用NetworkX計算最大子網的avg(l),運行了30 d沒有輸出結果.為了探究其時間復雜度,需要對較小規模的概念圖譜網絡進行計算.為此將共現次數作為閾值限制邊的數量從而形成不同較小規模的網絡,如表6所列.其中t為閾值,n為節點數,e為邊數.

圖6展示了NetworkX計算表6中各網絡平均路徑的實際運算時間time(s)與網絡規模(節點數n),經過擬合可知存在函數關系：time(n)=5.121×10—7×n2.236.當t=10時,NetworkX實際運行了1868428.416 s,約22 d.將最大子網節點數代入該函數可知NetworkX需要計算184 a,這也是計算30 d沒有輸出結果的原因.

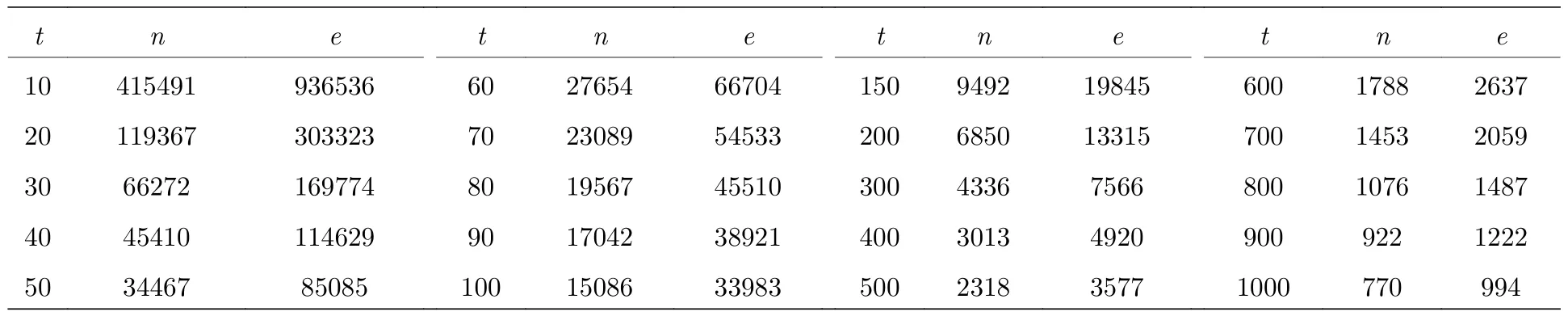
表6 部分閾值網絡及節點數Table 6.Threshold networks and the number of nodes.

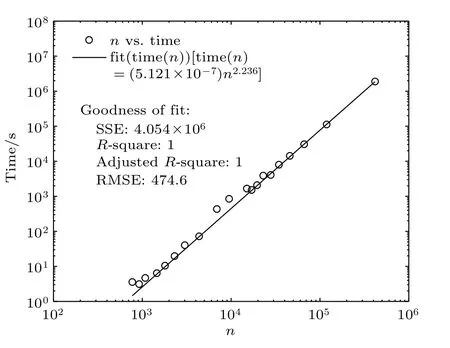
圖6 NetworkX計算平均路徑所需時間Fig.6.Time cost of NetworkX for avg(l).

隨后,嘗試用唐晉韜等[32]提出的CDZ方法進行計算.該方法首先根據局部中心性尋找區域中心點并據此對網絡進行區域劃分;之后用區域中心點的距離表示區域間節點的路徑長度,此時節點間路徑近似等于區域中心點的路徑與區域內路徑的和.其時間復雜函數為O(nlogn+e+d3),n是節點數,e是邊數,d是中心點數量[32].相對于隨機網絡,CDZ更適合具有無標度特征的復雜網絡.CDZ計算無標度網絡Cora平均路徑的時間為20余秒.Cora的n=30751,e=134450,按照文獻所述方法計算得到的d為46,因此時間復雜度函數值為369792.對于概念圖譜最大子網而言,n=15114834,e=32274081,d=130109,因此時間復雜度函數值為2202531075674600,是Cora的5956132434倍.按照CDZ計算Cora平均路徑用時為20 s計算,CDZ計算概念圖譜的最大子網平均路徑需要3777 a.

為此我們提出了一種概念圖譜網絡最短路徑長度的近似計算方法,該算法區別于CDZ的是用網絡層代替區域,且忽略同層內節點的具體距離.根據圖3所示的最大連通子網的層次結構,用層與層之間的距離近似代替點與點之間的距離,計算網絡的近似平均最短路徑長度：

其中AppAvg(l)表示網絡的近似平均最短路徑長度,minavg(l)表示可能存在的近似平均最短路徑長度的最小值,maxavg(l)表示可能存在的近似平均路徑長度的最大值.

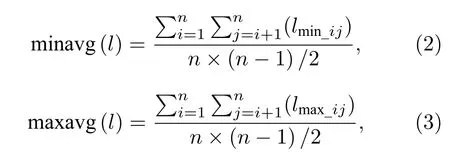
其中lmin_ij表示節點i到節點j可能的最小路徑長度,lmax_ij表示節點i到節點j可能的最大路徑長度.

由于網絡的層級關系,節點i到節點j之間必定存在一條路徑為(節點i,中心節點,節點j),此路徑為可能存在的最大的近似路徑,其距離公式為

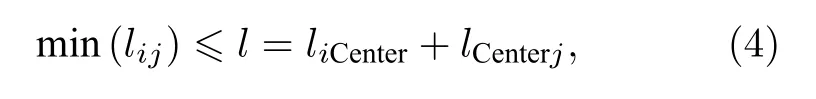
其中liCenter和lCenterj分別表示節點i到中心節點(Center)的距離和Center到節點j的路徑長度.根據對稱性,節點i到節點j與節點j到節點i的路徑長度相同.

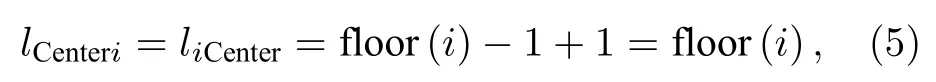
其中floor(i)表示節點i所在的層數.由于中心層包括兩個節點,所以在計算時統一為節點所在的層數減去1再加1.減1表示節點所在層數到中心層的路徑長度,加1表示中心層兩個節點之間的路徑長度.

表7為經過算法2的運行結果后統計的網絡層數及各層包含的節點數量.根據(4),(5)式以及表7計算得到子網中各節點之間的最大距離的和為770350922065817,代入(3)式maxavg(l)=6.74.

表7 子網結構與節點數量Table 7.Subnet structure and quantity of nodes.

假設每層節點到其他各層節點的最短距離為層數相減的絕對值,此時,節點對之間的路徑長度最短,有

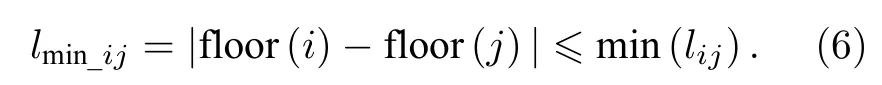
根據(6)式及表7中的數據可以求得子網節點間最小距離的和為125617583016439,將其代入(2)式可知最小近似平均最短路徑長度minavg(l)為1.10.所以子網的實際平均最短路徑長度處于(1.10,6.74)的開區間內,根據(1)式可計算得到網絡的近似平均最短路徑長度為3.92,表明知識圖譜網絡中的實體平均經過3.92個實體就可以到達任意實體的位置,概念圖譜網絡具有小世界的特性.相對于逐條匹配而言,以基于網狀拓撲結構進行的知識搜索更為迅速.

圖7是由NetworkX和本文方法計算的不同規模網絡的實際平均路徑RealAvg(l)和近似平均路徑AppAvg(l),n為節點數量.AppAvg(l)與RealAvg(l)變化趨勢相同,且隨網絡規模增加而減小,并穩定在一個4左右的定值.我們計算了各規模網絡平均路徑的真實值與近似值比值的平均值,有RealAvg(l)≈ 1.1×AppAvg(l).

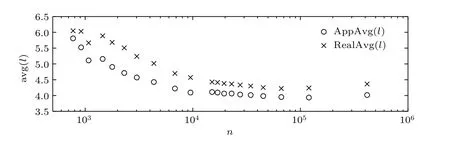
圖7 平均路徑精確值、近似值與節點數的關系Fig.7.Relationships of RealAvg(l)and AppAvg(l)ton.

根據隨機網絡平均最短路徑長度的估算公式計算相同規模隨機網絡的平均最短路徑為Lrandom～ ln(N)/ln(k)=11.38,其中N是最大子網的節點數,k=4.274是節點的平均度值,根據互聯網平均最短路徑長度[16]公式,可以計算得〈i〉～0.35 +2.06×lgN=15.14,可知概念圖譜網絡的節點間的聯系比同等規模的隨機網絡和萬維網節點間的聯系更緊密.此外,不同于互聯網平均最短路徑隨網絡規模的增大而增大,概念圖譜網絡的平均路徑隨網絡規模的增大反而減小,并最終趨近于一個4左右的定值.這一現象可能與概念圖譜的結構有關,為解釋此現象,對由算法2計算各閾值網絡最大子網時得到的網絡層次結構進行了統計.表8是各閾值網絡由中心層擴展時形成的層次結構及各層包含的節點數.

從表8可以看出,這些閾值網絡與概念圖譜最大子網在結構上十分相似,都形成了類似“菱形”結構：大量節點集中在中間靠前的網絡層,少量節點處于兩端的“邊緣”層.隨著網絡規模的增加,大量的節點更是集中在了前4層,表明大部分節點間經由中心層節點經過不超過4步就可到達彼此,可以一定程度地解釋概念圖譜網絡平均最短路徑隨著網絡規模增加而趨近于4左右這個定值的原因.概念圖譜反映的是知識間的聯系,可以將其看作人擁有的知識.通常一個人掌握的知識越多,其由一個知識推理或搜索到另外一個知識的速度也就越快.

4)聚類系數：聚類系數C是所有節點聚類系數的平均值,描述網絡中節點的聚集情況,即網絡緊密性.

對于度為1的節點,計算其聚類系數沒有實際意義,為此在計算網絡的聚類系數前首先要剔除度值為1的節點.在剔除度為1的節點后,最大子網還有5010477個節點.由于我們只有記錄最大子網邊信息的三元組的文本文件GraphLink,如果對每個節點直接計算其聚類系數,首先需要遍歷最大子網邊集合GraphLink得到該節點的鄰居節點集合,為此需調用3.3節中的GetNeighbor(Node,Graph)函數,并將參數Graph替換為GraphLink;之后再次遍歷GraphLink得到鄰居節點集合中存在的邊的數量,為此需再次調用GetNeighbor(Node,Graph),此處也應將Graph替換為GraphLink.參照3.4節中時間復雜度的分析,可知計算一個節點聚類系數的時間復雜度為以上兩個函數的時間復雜度之和,即2n+ 3.2n=5.2n,此處的n為GraphLink包含的邊數(32274033).由于需要計算聚類系數的節點數量為5010477,約為邊數的1/6,所以計算網絡的聚類系數的時間復雜度為5.2n×n×1/6 ≈ 0.867n2,時間復雜度仍較高,所以我們采用分段式計算方法.

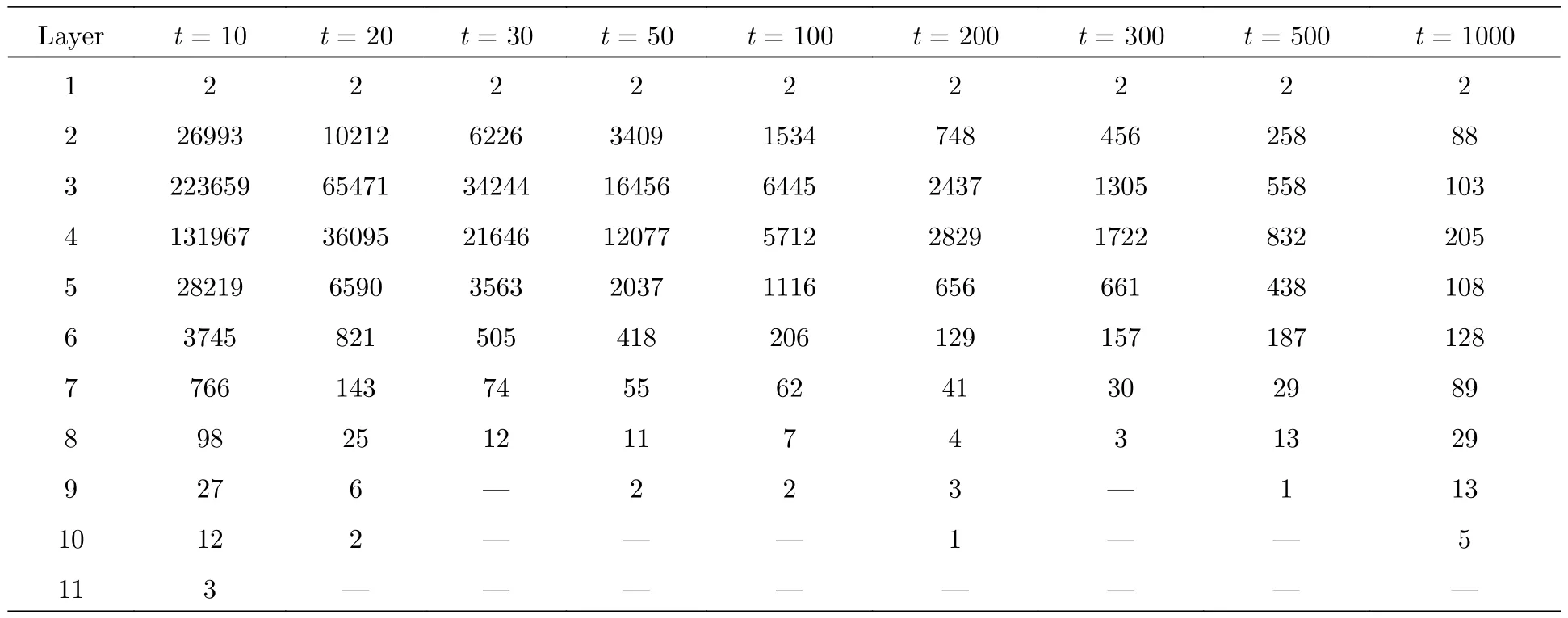
表8 不同閾值網絡的層次結構及各層的節點數Table 8.Layer structure and node number in each layer.

Nodeki表示度值為ki的節點的集合.根據度分布可知,度值越小,對應的節點數量越大,設定閾值θ=100.

對于度值大于θ的節點的集合Nodeki(ki=θ+1,θ+2,···,kmax,其中kmax表示節點的最大度值)：先根據最大連通子網的邊集合GraphLink尋找到每個節點Nodej∈Nodeki的鄰居節點的集合Neighborjki然后遍歷GraphLink中的每一條邊,對Nodeki中的每個Nodej,判斷該邊的兩個端點是否都屬于Neighborjki,若是,則表示該邊是連接Nodej的兩個鄰居節點的邊.度值為ki的各個節點的鄰居節點間的邊數構成邊數集合Edgeki,其存儲形式為k-value形式,如Edgeki={{Node1：edge1},{Node2：edge2},···,{Nodej：edgej}},其 中edgej為節點Nodej的鄰居節點間的邊數.節點Nodej的聚類系數計算公式如下：

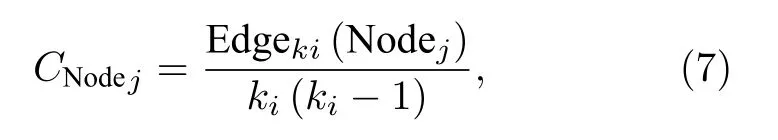
其中Edgeki(Nodej)表示Edgeki中與Nodej對應的edgej.

對于度值小于等于θ的節點集合Nodeki(ki=1,2,···,θ)：首先同上得到與度值ki對應的Nodeki及Neighborjki(j=1,2,···,length(Nodeki)),其中length(Nodeki)表示Nodeki中節點的數量;然后根據(Nodeki∪Neighborjki,j=1,2,···,length(Nodeki))從GraphLink中篩選與這些節點相關的邊,組成部分邊集合PartOfGraphki;再對PartOfGraphki中的每一條邊,對Nodeki的每個Nodej,判斷邊的兩個端點是否屬于Neighborjki,若是,則表示該邊是連接Nodej的兩個鄰居節點間的邊.得到度值ki對應的Nodeki中各個節點Nodej的鄰居節點間的邊數構成集合Edgeki,然后根據(7)式計算該集合中每個節點的聚類系數.

由于度值越小,節點數量越多,聚類系數就越難計算.在實驗中,度值在2—10范圍內的節點數占所有可計算聚類系數節點的89.66%,所以我們在度值小于閾值時引入Map/Reduce模式,將大型計算任務分解為多個小計算量任務,然后同時進行計算.對于度值相同的節點統一計算其聚類系數,在計算時分別計算分子,分母只需要計算一次(分母是相同的).并且,此種計算模式在分析度-平均聚類系數時也十分方便.

最大連通子網中聚類系數不為0的節點為1837431個,占12.16%,由全部節點聚類系數計算得到的網絡聚類系數為0.0468;剔除度值為1的節點后計算得到的網絡聚類系數為0.1410.為了判斷網絡的小世界特性,計算了相同規模(節點數量和平均度相同)的隨機網絡的聚類系數Crandom～k/N=2.83×10—7,其中N=15114834為節點數,k=4.274是網絡的平均度值[3].顯然概念圖譜網絡的聚類系數遠大于Crandom,可知概念圖譜網絡中節點聚群現象比較明顯.圖8是度值與平均聚類系數的關系,可知低度值節點的聚類系數較大,高度值節點的聚類系數普遍較小.

5)度相關性：度相關性描述的是節點之間根據度值作為相互之間連接的選擇偏好性,如度值為k的節點的鄰點平均度knn(k)隨k增加,表示度大的節點偏好連接其他度大的節點,則網絡是正相關的;反之,如果knn(k)隨k而減小,表示度大的節點偏好連接度小的節點,則網絡是負相關的.

表9列出了部分度值和該度值對應的所有節點的鄰點平均度,可知值最低的5個度其所有節點的鄰點平均度非常大,而值最高的5個度其所有節點的鄰點平均度相對而言卻非常小.

將度值k和與度為k的所有節點的鄰點平均度knn的關系繪制成圖9,可以看出,knn隨著k的增大而減小,呈現負相關性,表明概念圖譜網中與高度值節點相連接的節點的度值偏低,與低度值節點相連接的節點的度值偏高.

Newman[34]還給出了一種通過網絡節點度的Pearson相關系數r來判斷網絡相關性的量化方法,具體公式如下：

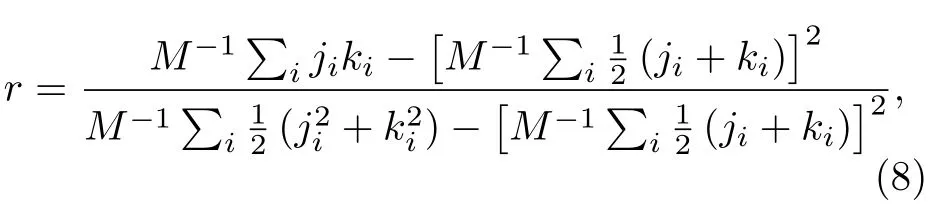
其中M表示網絡的邊數,ji和ki分別是第i條邊(i=1,2,···,M)的兩個端點的度值,r(—1≤r≤1)表示網絡相關性.經計算可知概念圖譜最大連通子網的相關性為—0.067,網絡是負相關的,與度值的鄰點平均度分析結論相同.同時,網絡的負相關性也保證了低度值節點可以與高度值節點相連,由于高度值節點可以連接到很多其他節點,所以在應用中可以實現推理過程.

6)知識丟失對概念圖譜完整性的影響：用節點刪除模擬知識丟失,通過隨機刪除和定向刪除(度值由高到低)分別測試了不同閾值下較小規模概念圖譜網絡的完整性.圖10(a)是閾值為500的實驗結果,x軸是節點刪除比,y軸是最大子網節點比例S,能夠一定程度上描述概念圖譜的完整性.隨機刪除對S影響很小,刪除80%以上的節點時S才接近0;定向刪除對S影響顯著,僅減少0.5%左右的節點時S就減少到了0.定向刪除下S的下降規律與computer network十分相似,快于同是無尺度網的BA網和科學合作網[35].

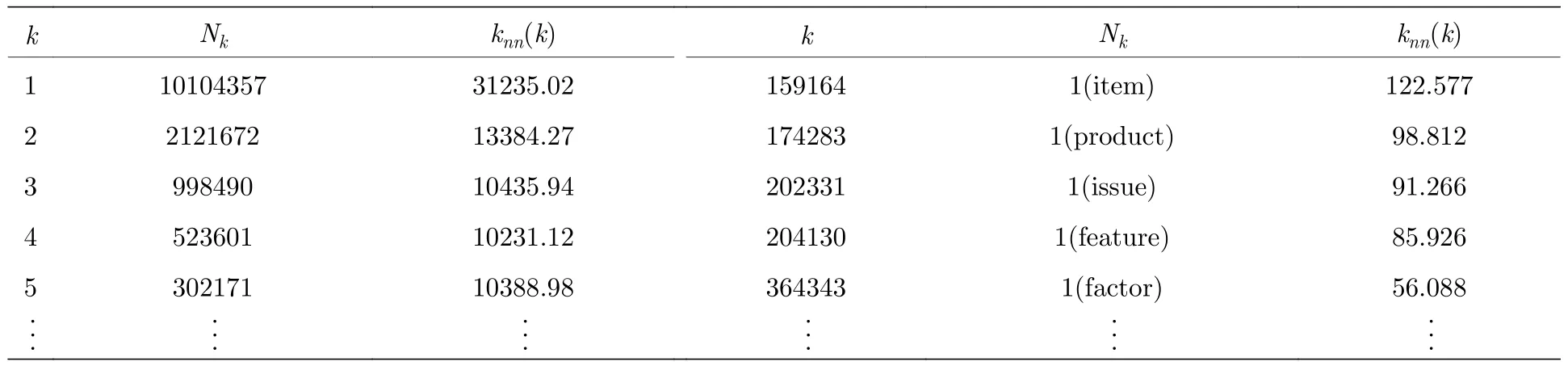
表9 部分度的節點數與該度值的所有節點的鄰點平均度Table 9.Part ofNkandknn(k).

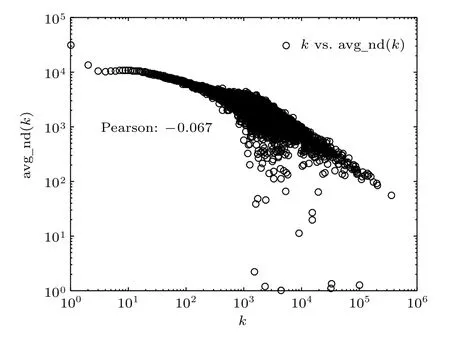
圖9 度-鄰點平均度相關性分析Fig.9.Analysis of degree and average degree of neighbor nodes.

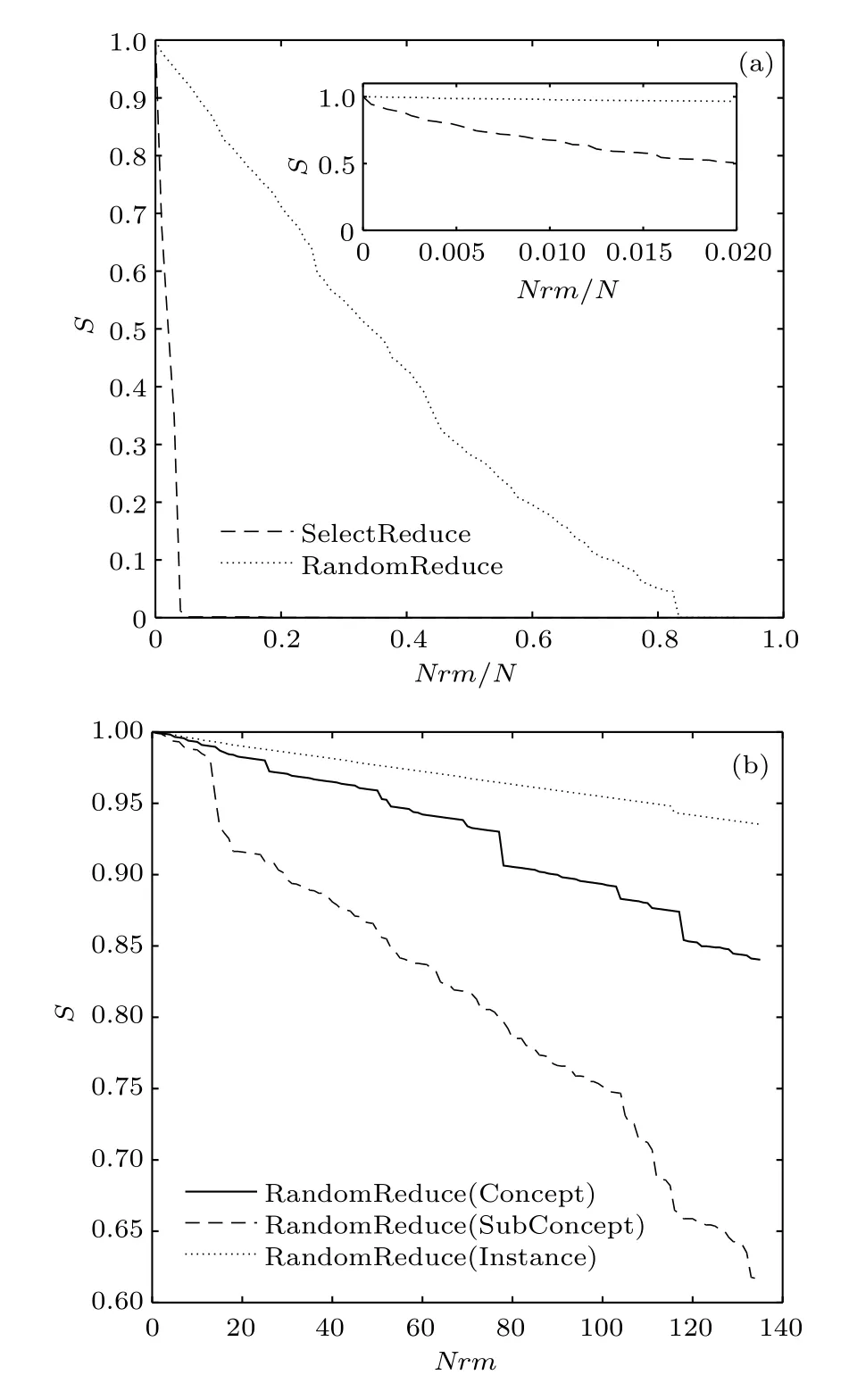
圖10 知識丟失對概念圖譜完整性的影響Fig.10.Size of the giant component when nodes are removed.

還測試了概念、實例、子概念丟失對概念圖譜完整性的影響,圖10(b)是隨機刪除1—140個三類節點時S的變化,可見子概念的丟失對圖譜完整性影響最大,其次是概念,最后是實例.為了分析以上現象,由度分布計算了各類節點的度期望值：概念節點的度期望為2.911,實例為1.899,子概念為36.214.也就是說隨機刪除1個概念同時丟失約3條邊(知識之間的聯系);隨機刪除1個實例同時丟失不到2條邊,隨機刪除1個子概念,平均會減少約36條邊,因此子概念的丟失對網絡完整性影響最大.

概念圖譜來源于數億用戶的搜索記錄,是反映人類對事物認知的知識庫.盡管每個人擁有的知識只是其中的一部分,但卻有類似的結構特征.即最具體的實例對于掌握知識而言重要性最低,而抽象的概念或子概念更重要.現實世界中,若忘記了某個實例,比如忘記了3是prime number (素數),只要掌握了prime number的概念,就可以推斷出3是prime number.但如果忘記的是概念或者子概念,如prime number,由3推理出prime number或其他素數就非常困難.

5 結 論

本文運用復雜網絡理論對由微軟概念圖譜所構建的概念圖譜網絡進行了分析.由于概念圖譜網絡中包含多個子網結構,提出了一種適合概念圖譜的最大子網抽取算法,實驗表明對于節點數量龐大的概念圖譜網絡,該算法在時間和空間上都優于NetworkX.在進行節點度分布分析時不但發現最大連通子網具有無標度特性,還發現子概念在概念圖譜中扮演著連接其他節點的角色.82%的實例節點只與一個概念存在IsA關聯,向我們揭示了實例詞在文本分析中通常不會因為一詞多義的原因導致理解上的歧義.為解決網絡規模巨大導致的計算困難,提出了一種近似網絡平均距離的計算方法,對比NetworkX和CDZ具有明顯優勢.分析表明概念圖譜網絡具有小世界特性,平均路徑隨網絡規模增加而減小并趨于定值4;概念圖譜網絡的“菱形”結構揭示了平均路徑趨于定值4的根源;平均路徑隨網絡規模增加而減小這一現象與人類認知和推理能力隨知識增加而提升這一現象一致.網絡聚類系數較大,網絡中節點的群聚現象較為明顯.根據度相關性的分析,可知網絡中與高度值節點相連接的節點的度值偏低,與低度值節點相連接的節點的度值偏高,度-平均度呈現負相關,有利于實現概念圖譜中的知識推理;概念圖譜完整性對知識的隨機缺失不敏感且子概念對概念圖譜完整性的影響明顯高于概念和實例.

考慮到概念圖譜的海量數據,以上對全網特性的分析都沒有考慮關系的方向和關系的緊密程度(邊的長度),在以后的工作中可以將關系的方向和邊長引入概念圖譜網絡模型的構建中,在此基礎上利用局部拓撲特性進行概念圖譜的自動補全研究.