二維含多孔介質周期復合結構聲傳播分析*
喬厚 何锃 張恒堃 彭偉才 江雯?
1)(華中科技大學力學系,結構分析與安全評定湖北省重點實驗室,武漢 430074)
2)(中國艦船研究設計中心,武漢 430064)
1 引 言
多孔介質是一類利用內阻尼耗散能量進而達到減振降噪的材料,由于造價低適用性好,這類材料和彈性體組成的復合結構在建筑、機械和航空航天等領域都有廣泛應用.
在含多孔介質復合結構的建模中,通常利用Biot理論[1]和等效流體模型[1]兩類模型描述彈性波在多孔介質中的傳播;但是,當考慮多孔介質固相骨架彈性特征時,等效流體模型不再適用[1,2],必須采用基于Biot理論的多孔介質模型.這類采用Biot理論討論的多孔介質夾層復合結構聲振問題,已經有很多研究[3-6].利用Allard等[7]和Deresiewicz[8]的簡化模型,Bolton等[3]采用Biot理論對二維夾層板結構的隨機聲傳播損失(STL)進行了研究,分析了幾種邊界條件下的結果;此后,Zhou等[4,9]、Liu等[5,10]以及Talebitooti等[11,12]也利用Biot理論對此類含多孔介質板殼夾層結構問題的三維情況進行了分析,并討論了外流等因素對STL的影響.此外,也有利用Biot模型結合數值方法進行這類復合結構問題研究[13-15].盡管這類含多孔介質復合結構具有優異聲學性能,對于中低頻問題,由于多孔介質在此頻域效果有限,并不能很好地提高復合結構的聲學性能[6].
由于具有優秀的中低頻特性,周期結構從20世紀50年代起就被廣泛研究[16,17];近年來,周期結構相關理論在聲子晶體[18]及超材料研究[19]等領域得到了廣泛應用.研究表明,周期結構對彈性波的調控機理有兩種[20,21],即布拉格散射和局域共振,前者對于低頻長波長彈性波適用性有限;因此,在中低頻短波長彈性波調制中,利用周期結構理論,由彈性體結合局域共振系統(彈簧-振子系統、Helmholtz振子等)構成的具有反常特性的周期復合結構(“超材料結構”)得到了廣泛研究和應用.近年來,此類周期復合結構在彈性波吸收[22]、聲波調控[21,23-25]與振動抑制[26,27]方面有很多研究進展,其中,理論[23,24,27]、實驗[23,27]和數值[22,26]方法都有應用.盡管如此,低頻寬帶輕質高效的聲振抑制問題,仍是理論與工程中有挑戰性的問題[28].
多孔介質是聲振控制中的輕質高效方案,而周期結構在中低頻應用中有優勢.研究表明,結合兩種方案可以取得更好的聲調控效果[29,30];然而,相關研究目前還不充分[6,31-33],其理論研究手段仍需要進一步發展;二者的協同機理也需要進一步探究.
為取得理想的中低頻隔聲特性,本文結合含多孔介質復合板和周期振子系統,組成了一種新型周期復合結構;隨后,采用等效動態質量描述振子系統,利用薄板理論和Biot多孔彈性方程建立了復合結構理論模型,分析了其在中低頻域的聲振特性,討論了多孔介質、周期振子等對此復合結構STL的影響.此外,對隔振結構中常見的組合振子系統,也討論了其隔聲可行性,并與簡單振子系統結果進行了對比分析.值得注意的是,結合周期振子和薄板結構的振動及聲學特征研究國內外已有很多[34-37],這里主要關注加入多孔介質后的復合結構隔聲特性,不再詳細說明附周期振子薄板結構結果,必要時直接引用對照.
2 復合結構及其相關理論和求解
圖1(a)為含多孔介質周期復合結構示意圖,此結構由多孔介質、薄板和周期分布的彈簧振子系統構成;彈簧振子系統沿x方向周期分布,周期間距為a;在每個周期內,假設含有Ns個振子(或振子系統),第i個振子的剛度和質量分別為ki和mi(i=1,2,· · ·,Ns).假定復合結構在y方向無限延伸,單位平面波以仰角φ入射,其速度勢為Φi=exp(jωt-jkr),其 中k=(kx,kz)為入射波 矢,r=(x,z)為位置矢量,下文中,簡諧時間項 e xp(jωt)都不再顯式寫出.
圖1(c)—(g)給出了復合結構的連接邊界條件和相應部分受力情況.多孔介質和板結構連接類型采用文獻[3]中的分類,記O類型為多孔介質開放邊界,即多孔介質界面直接與外部聲學域接觸;U類型為多孔介質間隔邊界,即多孔介質界面與彈性體間存在間隙(例如,薄空氣層);B類型為多孔介質固定邊界,即多孔介質界面與彈性體固定粘連.OU和OB類型為幾種類型邊界條件的組合,分別如圖1(c)和圖1(d)所示.當多孔介質與彈性體間為固定邊界時,由于多孔介質固相骨架中正應力和剪應力同時存在,此時彈性體還會受到面內外力和面外力矩作用,圖1(e)和圖1(f)給出了OU,OB兩種邊界情況下薄板法向的受力示意圖.
除采用圖1(a)所示簡單振子系統外,復合結構中的周期振子單元也可由圖2(a)和圖2(b)所示的組合振子系統構成,其相應的剛度、阻尼和質量如圖所示 (其中,參數kni,ζni和min中的n=1,2 為振子系統部件編號,i為周期單元序號).采用周期振子系統排布時,Ns≥1,可行的排布情況如圖3(暫不考慮三類振子系統混合分布的情況).為便于說明和分析,下文采用表1中縮寫形式描述圖3所示振子系統分布情況.
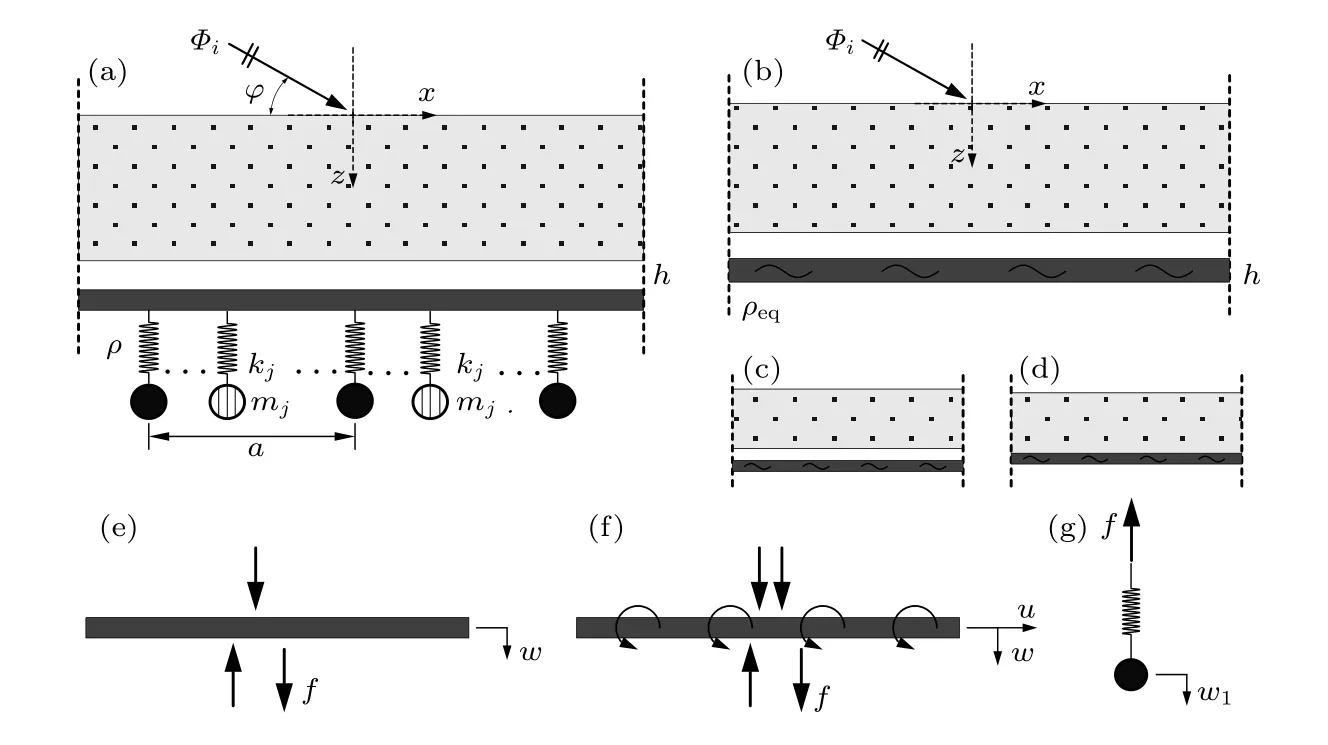
圖1 含多孔介質復合結構及其子結構示意圖 (a)含多孔介質復合結構;(b)等效模型;(c)OU邊界;(d)OB邊界;(e)板受力情況(OU邊界);(f)板受力情況(OB邊界);(g)彈簧振子受力Fig.1.Schematic of the poroelastic composite structure and its substructures:(a)The poroelastic composite structure;(b)the equivalent model;(c)the OU boundary connection;(d)the OB boundary connection;(e)the forces in OU boundary case;(f)the forces in OB boundary case;(g)the forces in a simple spring-mass resonator.

圖2 組合振子系統示意圖 (a)串聯彈簧振子系統A;(b)復合彈簧振子系統BFig.2.Schematic of the composite-resonator-structure:(a)Composite resonator type A,two resonators placed in serial connection;(b)composite resonator type B,two resonators placed in composite connection.
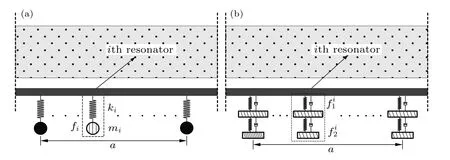
圖3 周期振子排布方式示意圖 (a)簡單振子周期分布,按各個振子質量mi和特征頻率fi分為多個振子情況 (N1SR,mi和fi均保持恒定)和多種振子情況 (NNSR,mi或fi不相同);(b)組合振子周期分布,按振子部件質量和特征頻率分為多個振子情況 (N1CR,和均保持恒定)和多種振子情況 (NNCR,或不相同);圖中虛線框內部分為單個振子單元,(b)中虛線框部分可替換為 圖2中B類組合振子Fig.3.Schematic of the arrangement of periodic resonators:(a)An array of simple resonators,denoted as multiple resonators(N1SR,with constantmiandfi)or multiple kinds of resonators (NNSR,with differentmiandfi);(b)an array of composite resonators,denoted as multiple resonators (N1CR,with constantand )or multiple kinds of resonators (NNCR,with different or).The area in the dash-line denotes the periodic lattice,in panel (b),the composite resonator can be type B in Fig.2.
2.1 彈性骨架多孔介質模型
常見多孔介質固相骨架可以有彈性變形,此時必須采用Biot理論[38]描述多孔介質中彈性波的傳播.考慮圖1(a)所示周期復合結構,以多孔介質固相位移和液相位移描述的多孔介質中彈性波傳播方程為[38]
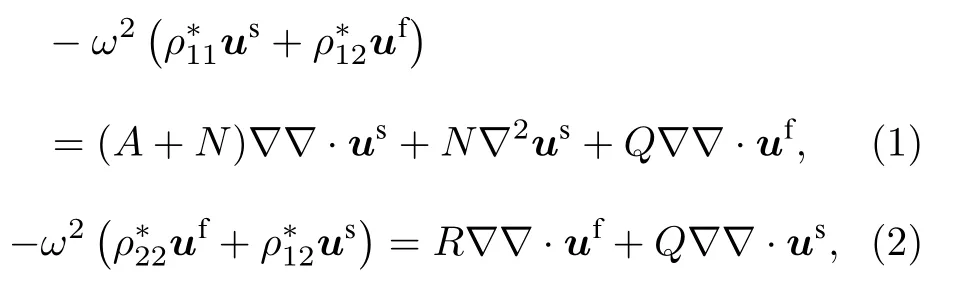
平面波入射情況下,二維多孔介質域中的場變量,如應力和位移等,都可以由6個待定未知諧波貢獻量Ci(i=1,2,···,6)唯一確定[3,6],詳細的推導方法和表達式可參考文獻[3,6],這里不再贅述.

表1 振子系統分布情況簡稱及其對應含義Table 1.Abbreviations of the distribution of resonator systems and their meanings.
2.2 薄板-振子耦合結構理論模型
對于中低頻問題,關注的頻域低于板臨界頻率(coincidence frequency),故采用薄板理論描述彈性波在板中的傳播[39].在外力和外力矩同時作用時,薄板的面內振動和面外振動方程分別為[6]

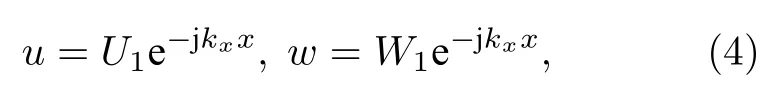
其中,U1和為可由復合結構邊界條件確定的待定諧波幅值.
根據文獻[35,41],對中低頻問題,彈簧振子系統可以等效為板上的附加質量塊,其效果相當于增加了板密度,相應結果與平面波展開法的結果完全一致,但是計算量大為降低[35].因此,這里采用等效介質模型[35]描述薄板-振子耦合結構,其做法是將周期單元內的彈簧振子系統等效為附加在均勻板上的額外質量,相當于改變了板密度.對圖1(a)所示的簡單振子系統,假定第i個振子的恢復力為fi,i=1,2,···,Ns,則
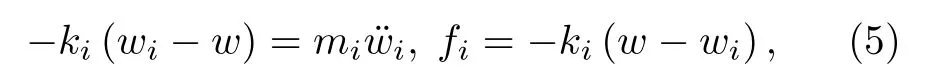
其中,wi為第i個振子的質量塊位移.記第i個彈簧振子動態質量為meq,i(ω),根據fi=meq,i,則meq,i(ω)為
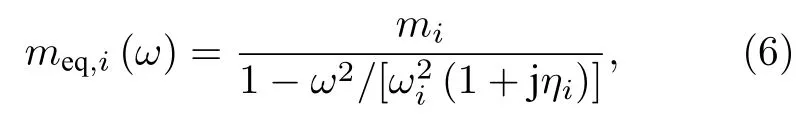
其中,mi為振子質量,ωi為振子特征圓頻率,ηi為彈簧阻尼系數;此結果與文獻[35,41]一致.根據(6)式,對于單位寬度薄板-簡單振子耦合結構,其等效動態密度為
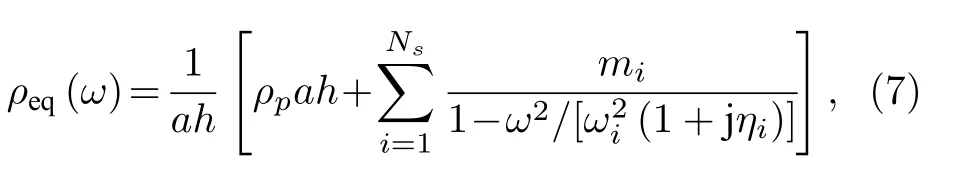
其主結構的位移傳遞率(displacement transmissibility)Ti(ω)=wi/w為
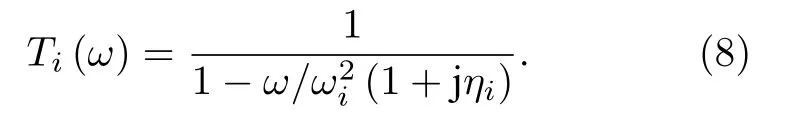
對于圖2(a)和圖2(b)兩種組合振子系統情況,相應的振子系統方程為
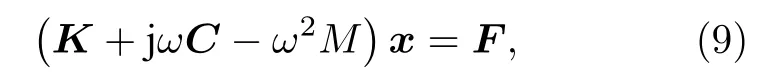
其中,x=[x1,x2,x3]T=[w1/w,w2/w,f/w]T;f為主結構(薄板)對振子系統作用力;F為右端參數項;兩類組合振子系統的質量矩陣M、阻尼矩陣C和剛度矩陣K均在附錄A給出.由(9)式可得

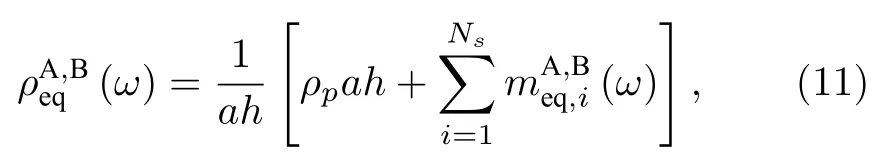
其中,上標A,B分別對應圖2中復合振子系統(a)和(b);式中,上標A,B一一對應取得.
2.3 復合結構中的聲學域
復合結構周圍的聲學域由聲速度勢Φ描述,它滿足聲學域波動方程
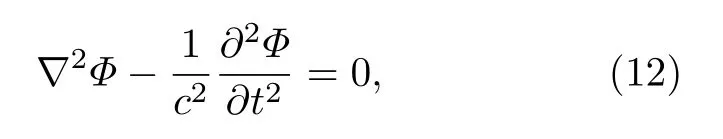
其中,c為相應聲學域中波速.對于OU邊界情況,假定其入射側聲學域速度勢Φ1,多孔介質和薄板間空氣層速度勢Φ2和透射側速度勢Φ3分別如下:
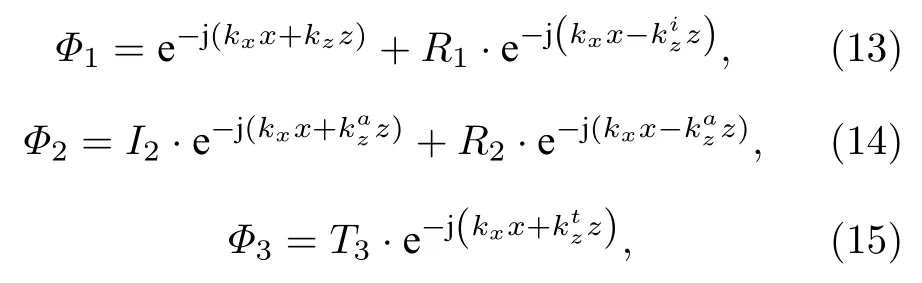
其中R1,I2,R2和T3為待定諧波幅值,由下文邊界條件確定.由(12)—(15)式可得
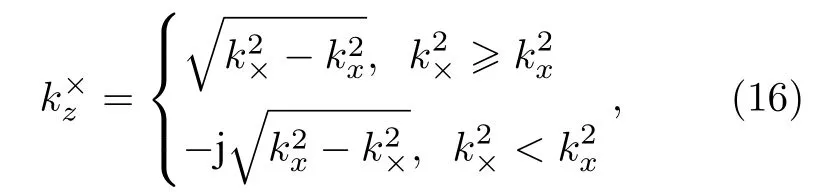
2.4 復合結構邊界條件及求解
在文獻[3,4]中,多孔介質和相鄰聲學域或彈性體連接的O,U和B三種情況邊界條件方程已經被詳細討論給出,這里不再說明.以OU邊界情況為例,以下給出與本文相關的復合結構邊界條件來說明求解過程.相關方程為

其中,?為多孔介質孔隙率;ρi,ρa和ρt分別為入射側、空氣夾層和透射側聲學域介質密度;s為多孔介質液相壓力;σz和τzx為多孔介質固相正應力和切應力;式中方程 (i)—(xi)都施加在復合結構中不同域交界面或薄板中面上.
根據文獻[3,4,6],利用(4),(13)—(15)式,(17)式可整理為

其中,未知矢量x=[C1,C2,C3,C4,C5,C6,W1,R1,I2,R2,T3]T,系數矩陣A和力向量f在附錄B中給出.根據(18)式,可求得x=A-1f,由此可得聲學域聲速度勢和多孔介質場及薄板位移.
聲學域聲功率定義為
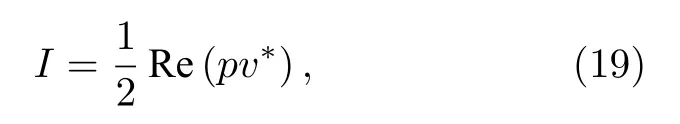
其中,聲壓p=ρ?Φ/?t,速度v=-?Φ,v*為法向速度v的共軛復數.聲功率傳遞系數定義為τ=It/Ii,Ii和It分別為入射聲功率和透射聲功率;對于散射聲場,其隨機傳聲損失(STL)為[3,35]
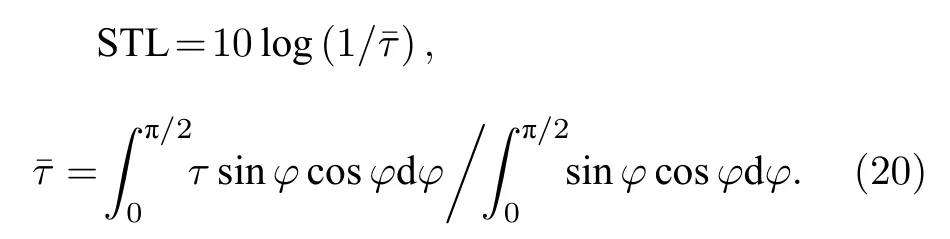
根據(18)式的結果即可求得復合結構的聲功率傳遞系數和STL.
3 模型驗證及分析
選取薄板、空氣域及簡單振子參數如表2所列.
表2中,fr為圖1 (a)簡單振子特征頻率;γ=msum/(ρpha)為振子系統總質量與薄板單位寬度總質量的比值,以下簡記為振子系統質量比.多孔材料參數如表3所列.
表3中,ρs和ρf分別為多孔介質固相和氣相密度,Es和νs為其固相楊氏模量和泊松比,?為孔隙率,τ∞為幾何形狀因子,σ0為流阻,hp為多孔介質厚度.采用一維Simpson積分計算復合結構的STL,積分步長取為 π /180,計算頻域為1—1000 Hz.下文如無特殊說明,所有計算均采用上述計算設置.

表2 薄板、空氣域及振子參數Table 2.Parameters of plate and resonators.

表3 多孔材料參數Table 3.Parameters of the porous media used here.
3.1 模型驗證
為驗證本文的理論模型,分別將其退化為文獻[35]中附加亞波長周期振子的均勻薄板結構模型(?=1,hp=ha=0,圖4(a)為隨機入射情況,圖4(b)為斜入射情況)及文獻[3]中多孔介質復合結構模型(msum=0,圖4(c)),并選用相同計算參數與相應結果進行對照,驗證算例模型示意圖及其結果在圖4中給出.
從圖4可以看出,對于附加周期振子均勻薄板和含多孔介質復合板兩種情況,本文方法計算得出的結果與相應文獻中數據都符合良好,表明本文方法是可靠的.
3.2 附加多孔介質對復合結構STL的影響
保持振子系統質量比γ=0.2,取復合結構中周期簡單振子質量塊m0=27g (N1SR情況),有無多孔介質時兩種邊界條件下的STL情況見圖5.
由圖5可以看出,在OU和OB兩種邊界條件下,附加多孔介質對復合結構STL影響情況基本一致.采用某一特征頻率振子時,多孔材料的引入可以在遠離振子特征頻率頻域提升其STL,這是由多孔介質的聲學性能決定的.周期振子特征頻率附近,有無多孔介質對STL提升并不明顯,此區域STL主要由周期振子決定,但由于多孔介質的引入,在振子系統特征頻率后的STL降低趨勢被削弱.因此,多孔介質的引入,總體上增大了結構的隔聲能力,這與文獻[1]中對多孔介質的特性描述一致.

圖4 不同類型隔聲結構驗證算例 (a)文獻[35]隨機入射情況;(b)文獻[35]斜入射情況;(c)文獻[3]含多孔介質復合結構;其中,各曲線為本文結果,各標記為文獻中結果Fig.4.Validation of the results here with previous results:(a)The diffuse case in Ref.[35];(b)the oblique incident cases in Ref.[35];(c)the composite poroelastic structure without resonator in Ref.[3].The lines are results obtained here,while the marks are the results in the references.
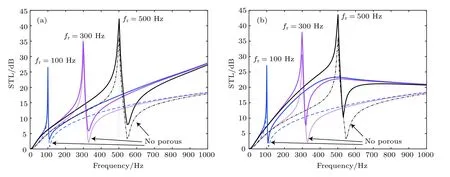
圖5 有無多孔材料對含不同特征頻率振子系統復合結構STL的影響 (a)OU邊界情況;(b)OB邊界情況;有無多孔介質分別與相應實線和虛線對應Fig.5.Influence of porous material on the STL of the multiple-single-type-resonator composite structure with different characteristic frequencies:(a)OU case;(b)OB case.The solid lines correspond to cases with porous materials.
圖6給出了兩種邊界條件下含相同簡單振子系統復合結構(fr=300 Hz)有無多孔介質情況,及相應不含振子復合結構的STL.由圖6可知,采用某一特征頻率振子時,多孔材料的引入可以在遠離振子特征頻率頻域提升其STL,最終趨近于相應不含振子復合結構的STL.采用多孔介質和簡單周期振子復合結構,可以使得結構的隔聲性能在保有多孔介質寬頻優勢情況下,在特定頻點或頻段有一定提升;或保有簡單周期振子系統特定頻點或頻段優勢情況下,在寬頻域有一定提升.
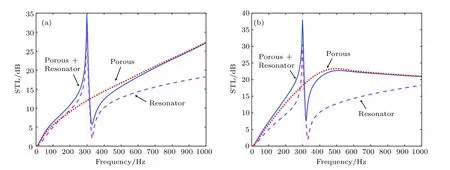
圖6 含相同簡單振子系統復合結構(fr=300 Hz)有無多孔介質及相應不含振子復合結構的STL (有多孔介質,Porous +Resonator;無多孔介質,Resonator;相應不含振子復合結構,Porous)(a)OU邊界情況;(b)OB邊界情況.Fig.6.The STL of multiple-single-type-resonator composite structure (fr=300 Hz)with/without porous,and composite structure without resonators:(a)OU case;(b)OB case.Composite structure here with porous material:Porous + Resonator.Without porous material:Resonator.Composite structure without resonators:Porous.
3.3 周期間隔內分布多個振子系統時STL情況
3.3.1 N1SR-簡單振子系統情況
保持振子系統質量比γ=0.2,取復合結構中周期簡單振子質量塊m0=27 g,采用不同特征頻率簡單振子系統時,復合結構在OU和OB兩類邊界條件下的STL如圖7(a)和圖7(b).由圖7可知,采用不同特征頻率的周期振子系統,都使得在此特征頻率附近STL先顯著提升然后降低,最后恢復到不含振子時STL的水平.這表明,合適引入和布置周期振子,可以在一定頻域內達到提升STL的目的.
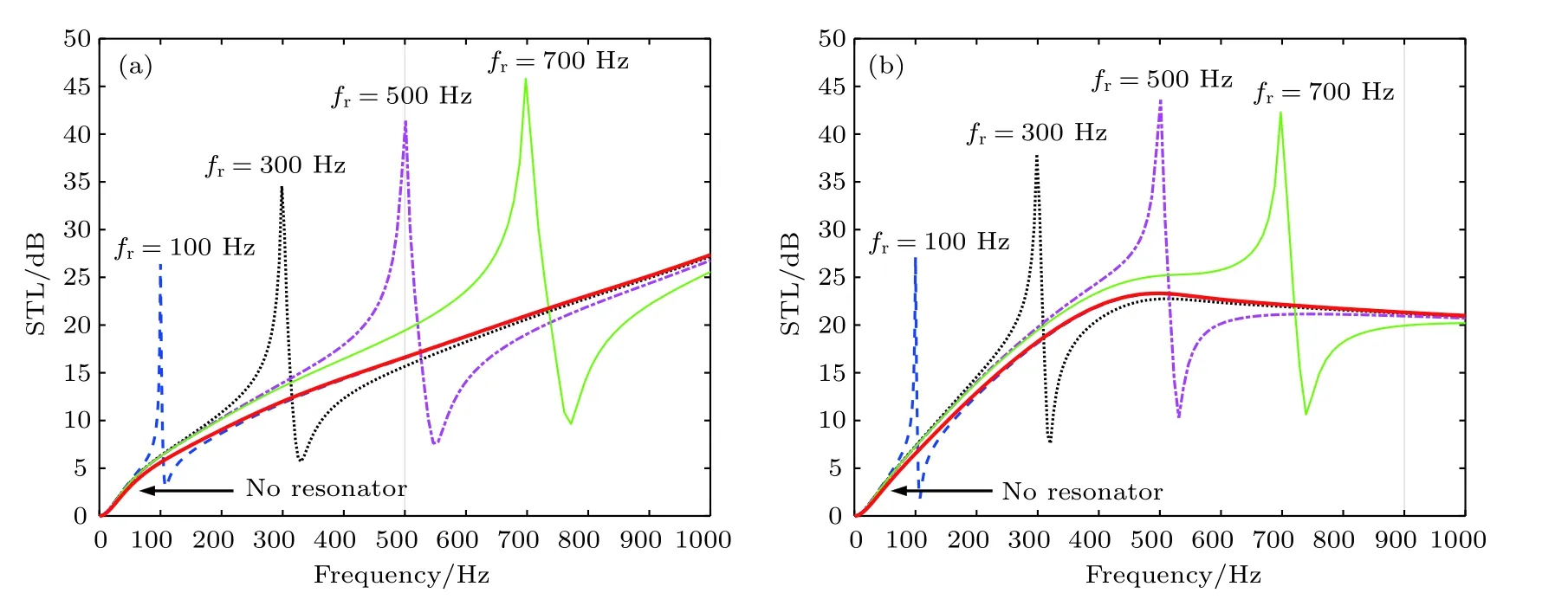
圖7 采用不同特征頻率簡單振子系統對復合結構STL的影響 (a)OU邊界;(b)OB邊界Fig.7.Influences of resonators with different characteristic frequencies on the STL:(a)OU case;(b)OB case.
圖8(a)和圖8(b)給出了兩種邊界條件下,由特征頻率fr=300 Hz的簡單振子構成的復合結構的STL及其位移傳遞率Ti、振子動態質量meq和板等效動態密度ρeq.從圖8可以看出,在振子特征頻率附近Ti,meq和ρeq變化趨勢一致,都由極大(f=290 Hz)下降為極小(f=307 Hz);STL也呈由極大(f=298 Hz)到極小(f=325或335 Hz)的變化趨勢,但STL變化與Ti,meq和ρeq變化特征并不同步,存在一定的頻率滯后.這是由于局域共振板在特征頻率附近存在一個范圍約為fr到fr(1+γ)1/2的帶隙[34,35],而fr處板等效動態密度呈極大值(無阻尼時為無窮大),fr(1+γ)1/2處呈極小;此頻域為質量定律控制區域[42],其隔聲量(即STL)與結構面密度呈正相關,故該頻域內STL呈極大過渡到極小趨勢.
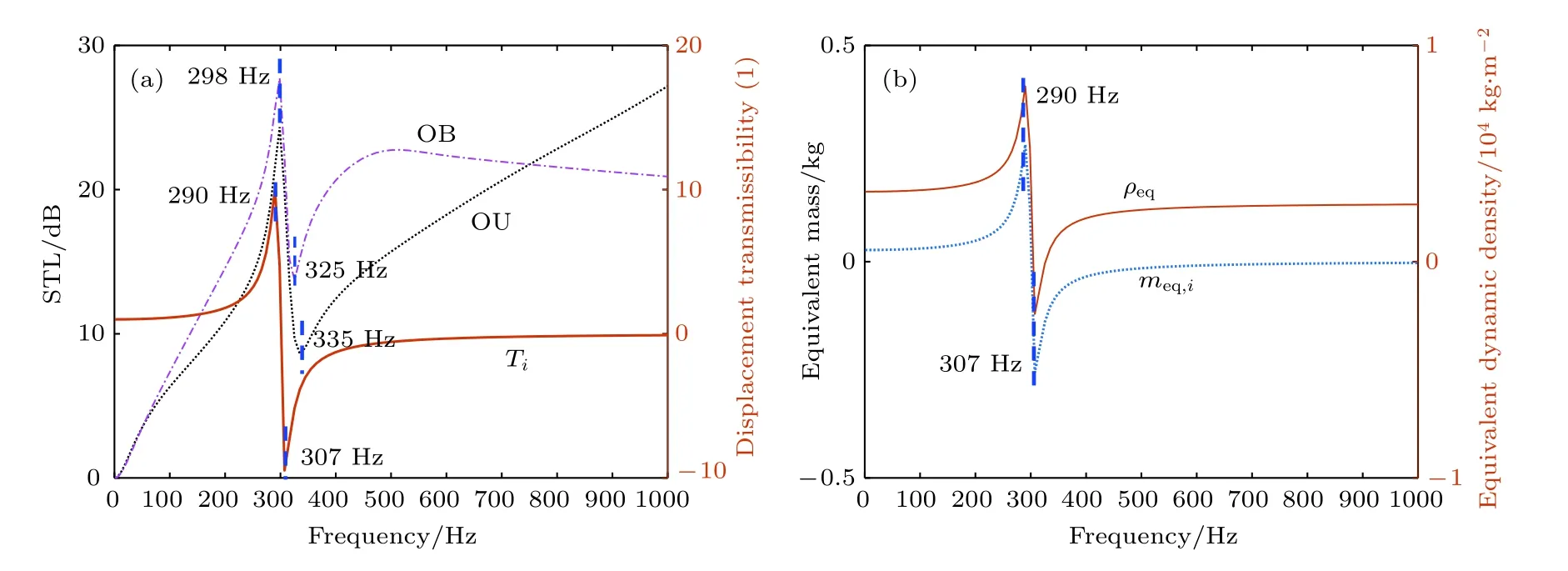
圖8 單一類型簡單振子周期排布時 (a)OU,OB情況下STL及其位移傳遞率Ti;(b)振子的等效質量meq和板等效動態密度ρeqFig.8.(a)STL of OU and OB case in periodically-arranged single simple resonator case,and its displacement transmissibilityTi;(b)equivalent massmeqof a single resonator and the dynamic densityρeq of the equivalent plate.
3.3.2 N1CR-組合振子系統情況
不同振子系統的動態特性不同,使用合適的組合振子系統可以一定程度上拓寬振子系統的作用頻域,進而達到更寬頻帶振動調控[43].為便于討論,令組合振子系統A,B中振子質量剛度分別滿足如下關系其阻尼比為對無阻尼情況 (即),組合振子系統A特征圓頻率為

(21)式與文獻[43]中無阻尼組合振子結果一致.同樣,無阻尼組合振子系統B的特征圓頻率為
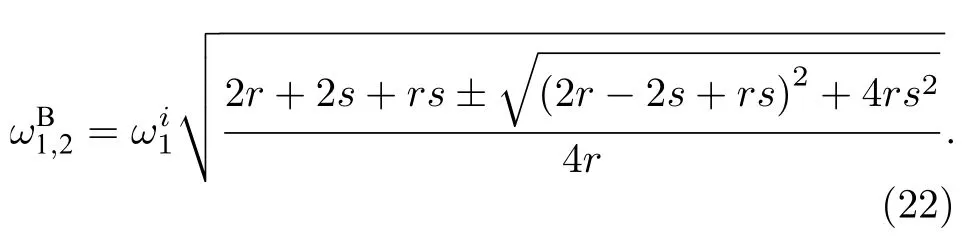
由(21)和(22)式可知,組合振子A和B二特征頻率間的帶寬為B.根據前述分析,復合結構STL在振子特征頻率附近呈由極大到極小變化趨勢,為獲得較高STL,組合振子二特征頻率間帶寬 Δfi應控制到合適水平,相關研究還在進行中,這里僅給出一些初步結果.忽略彈簧質量,保持振子系統質量比γ=0.2,取組合系統參數如表4所列.

表4 振子系統參數Table 4.Parameters of the composite resonators.
組合振子系統 A和B 的位移傳遞率T1,T2和動態質量meq變化情況見圖9.
由圖9(a1)和圖9(b1)可知,在組合振子系統A和B的共振頻率附近,系統中振子位移傳遞率均呈先增大至共振頻率再降低的趨勢,且振子系統A和B兩個共振頻率之間形成了一段振動抑制頻帶,此頻帶寬度與組合振子系統特征頻率有關;組合振子系統A和B均可以對主結構振動產生明顯抑制,但其抑制帶寬不同.由于聲波通過此復合結構中薄板(主結構)向透射側傳播,針對薄板向外部輻射聲的振動模態采用合適的組合振子系統,預計可以改善結構隔聲性能.
圖10顯示了保持振子系統質量比γ=0.2,單周期內分布Ns=4 個相同簡單振子,組合振子A或B和不含振子時復合結構的STL情況.由圖10可知,在兩種邊界條件下,由于振子系統特征頻率附近其STL呈先升高后降低趨勢,對單一共振頻率的簡單振子系統,其STL提升頻域較窄;選用合適參數的組合振子系統A或B,相對簡單振子系統,可以在較寬頻域提升復合結構的STL,同時不顯著降低其STL值.
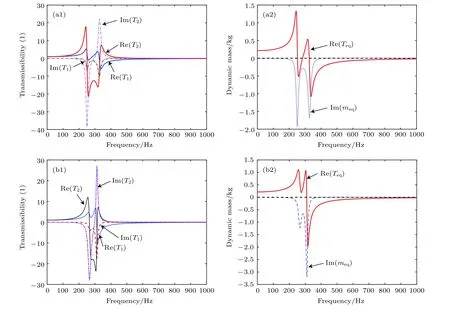
圖9 兩類組合振子系統中質量塊的位移傳遞率T1,T2和動態質量meq(a1)組合振子系統A中各質量塊的位移傳遞率T1,T2;(a2)組合振子系統A的動態質量meq;(b1)組合振子系統B中各質量塊的位移傳遞率T1,T2;(b2)組合振子系統B的動態質量meqFig.9.Displacement transmissibility and dynamic mass of the mass components in the two composite resonators:(a1)Displacement transmissibilityT1,T2of composite resonator type A;(a2)dynamic massmeqof composite resonator type A;(b1)displacement transmissibilityT1,T2of composite resonator type B;(b2)dynamic massmeqof composite resonator type B.
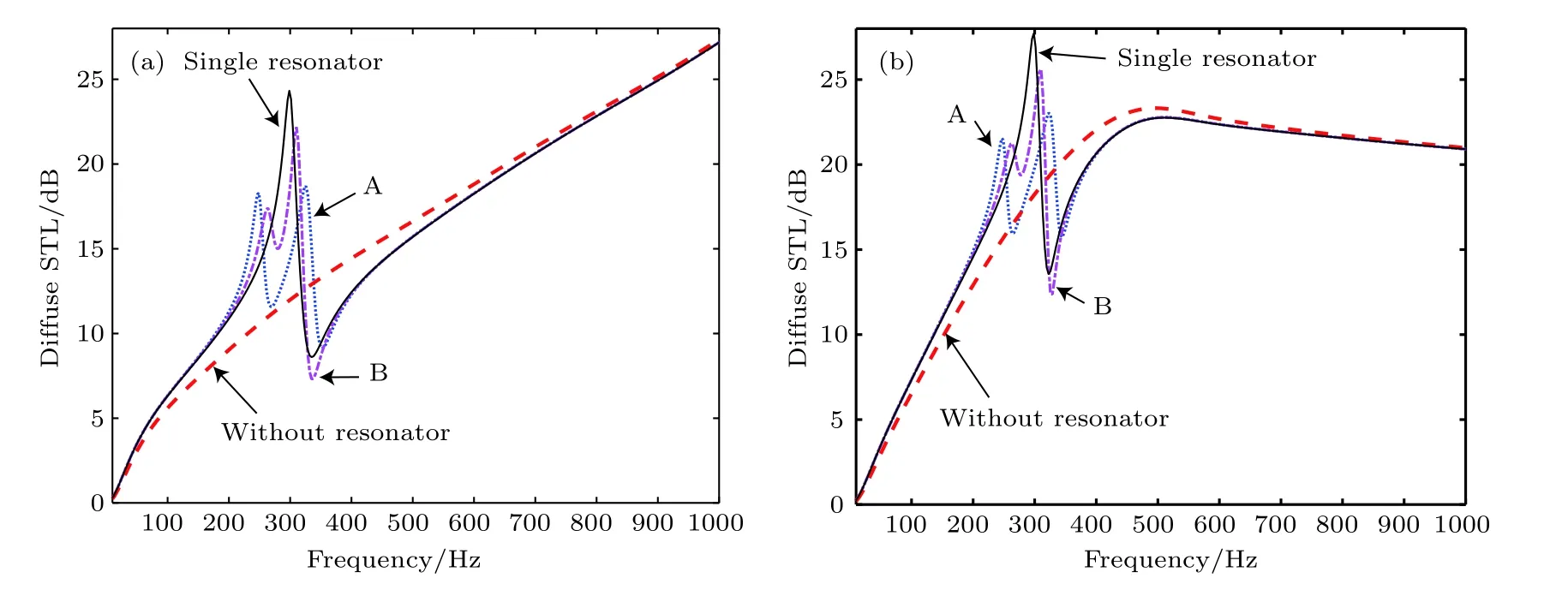
圖10 復合結構周期間隔內分布4個相同簡單振子(Single resonator),組合振子A或組合振子B時的STL和不含振子復合結構(Without resonator)的STL (a)OU邊界情況;(b)OB邊界情況Fig.10.STL of the proposed composite structure with 4 identical simple resonators (Single resonator),composite resonators of type A or B versus its STL without any resonators (Without resonator)in a periodic lattice:(a)OU boundary case;(b)OB boundary case.
3.4 周期間隔內分布多種振子系統時STL情況
在周期單元內布置多種振子(或組合振子),可以拓寬復合結構的振動抑制頻帶[35],進而提高其STL水平.以下保持振子系統質量比為0.2,分析采用多種振子系統對復合結構的聲調控效果.
3.4.1 NNSR-簡單振子情況
選取不同特征頻率簡單振子系統,討論以下兩種情況復合結構的聲調控特性:(A)等質量振子,振子質量mi為振子系統總質量msum的 1/Ns;(B)振子質量mi各不相同,mi=m0+(i-1)Δm,i=1,2,···,Ns.假定彈簧阻尼系數為ηi=0.05.圖11給出了OU,OB兩種邊界情況下NNSR分布時情況A,B的結果,其中振子特征頻率分別為=300+50(i-1)(Hz),i=1,2,· · ·,Ns,Ns=4,5,6,7.
由圖11可知,特征頻率各不相同的多振子系統,無論其各振子質量是否相等,都能在由振子特征頻率決定的頻帶提升復合結構STL,此結論與文獻[35]中相似;同時,非均勻質量分布的周期振子對復合結構的STL提升更為明顯,缺點是在振子特征頻率決定的頻帶之外,其STL下降也更為劇烈.這是由振子質量的不均勻分布決定的.此外,兩類邊界情況下不含振子復合結構的STL變化情況不同,此結果決定了復合結構STL的整體趨勢.若僅考慮某頻率范圍的隔聲性能,采用不同振子,按照振子特征頻率依次增大,振子質量依次遞增布置方案,可以提升對應頻率范圍的隔聲性能.
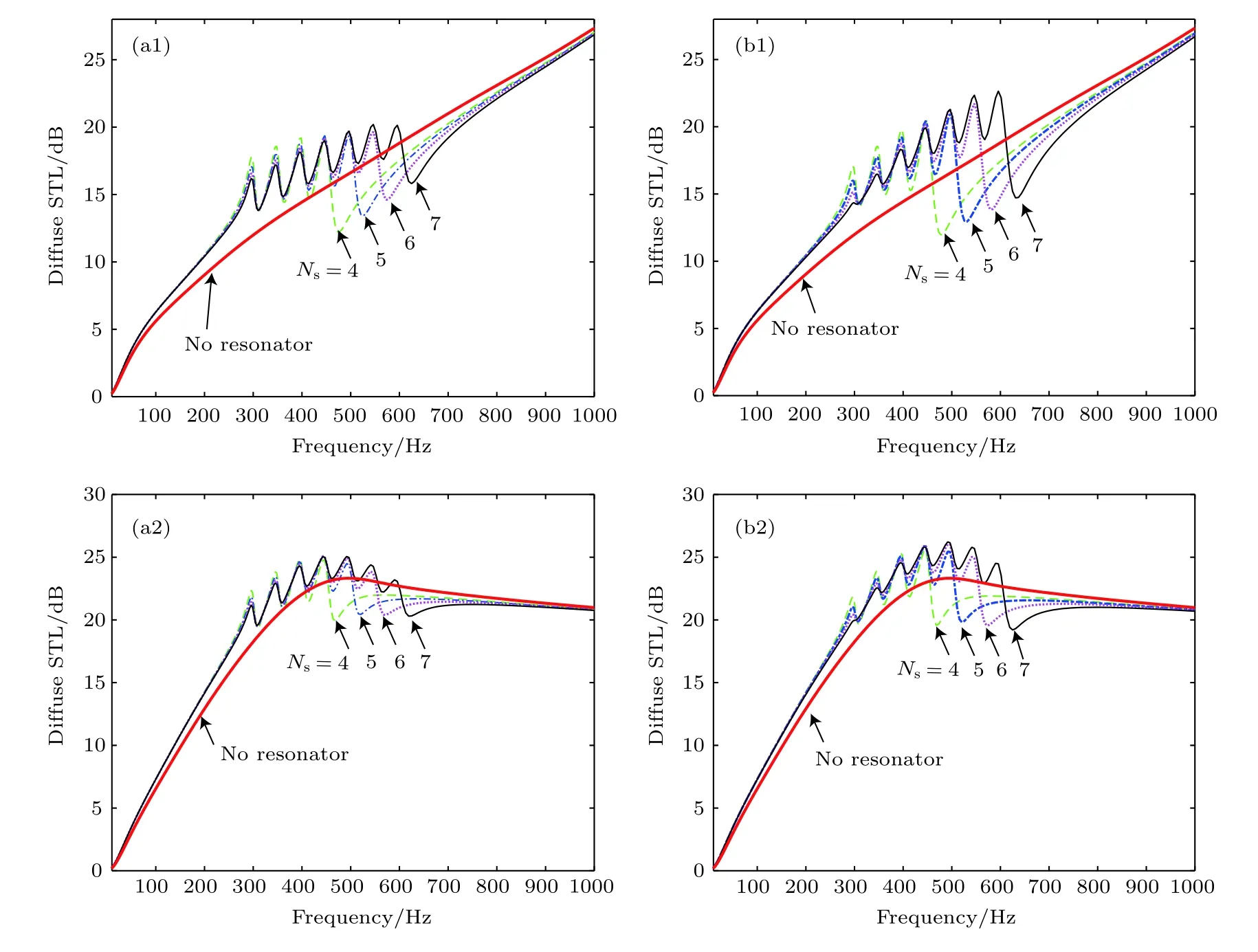
圖11 NNSR分布時OU,OB邊界情況下的STL (a1),(a2)情況A;(b1),(b2)情況B,Δm/msum=0.04;其中,(a1)和(b1)為OU邊界情況,(a2)和(b2)為OB邊界情況Fig.11.STL of the composite structure with NNSR configuration under two boundary cases:(a1),(a2)Case A;(b1),(b2)case B,Δm/msum=0.04.Here (a1)and (b1)correspond to OU case,(a2)and (b2)correspond to OB case.
3.4.2 NNCR-組合振子情況
忽略組合振子中的彈簧質量,保持振子系統質量比γ=0.2,選取組合振子系統參數如表5所列.

表5 組合振子系統參數Table 5.Parameters of the composite resonators.
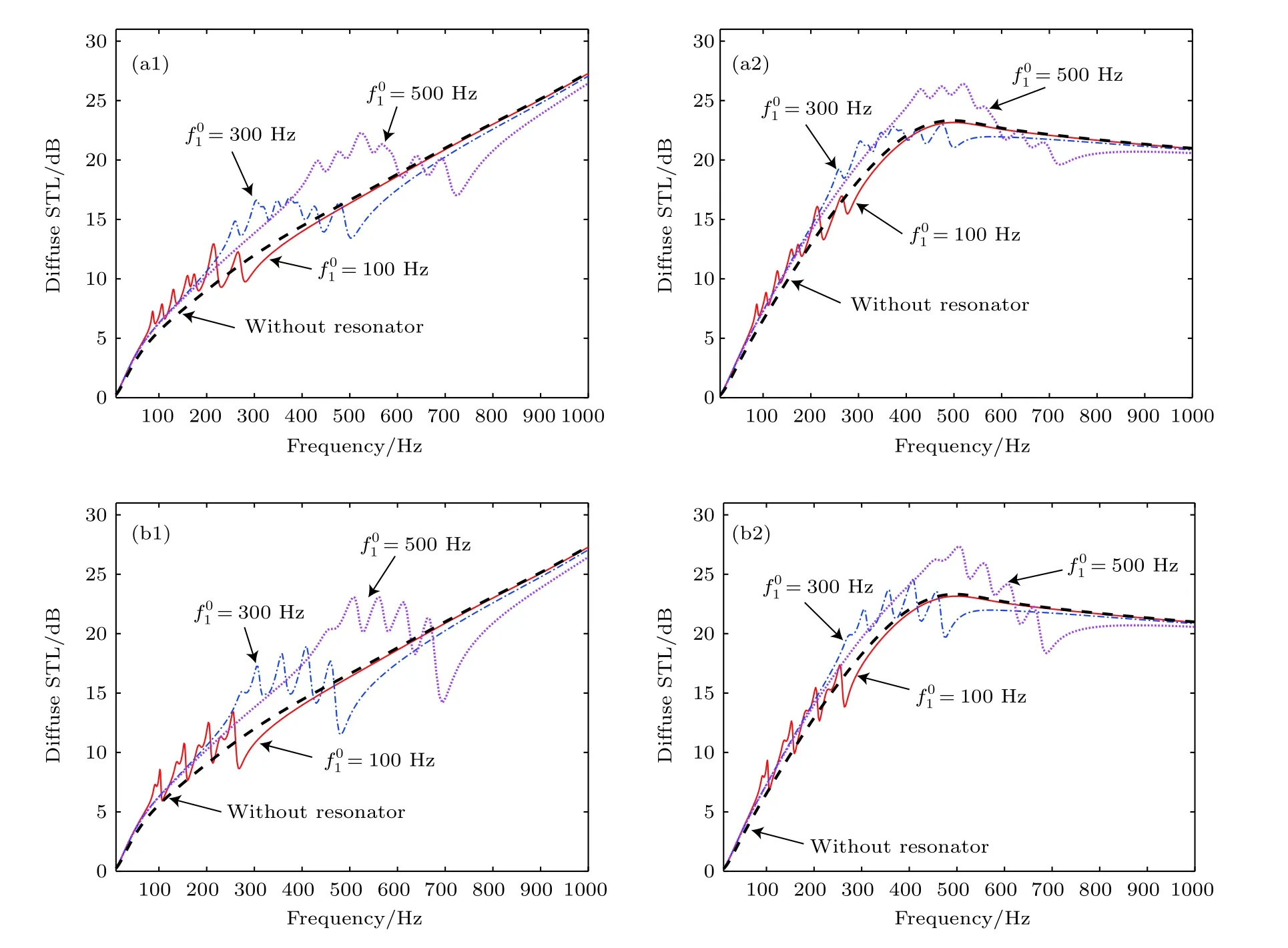
圖12 采用組合振子復合結構的STL (a1),(a2)采用組合振子A;(b1),(b2)采用組合振子B;其中,(a1)和(b1)對應于OU邊界情況,(a2)和(b2)對應于OB邊界情況Fig.12.STL of the proposed composite structure under NNCR configuration:(a1),(a2)Composite resonator type A;(b1),(b2)composite resonator type B.Here (a1)and (b1)correspond to OU case,(a2)and (b2)correspond to OB case.
由圖12可知,在單個周期內引入多個不同特征頻率的組合振子,同簡單振子情況類似,可以提高復合結構在其特征頻率決定的頻域內的STL,在此頻域內,OU和OB兩種邊界條件下呈現了類似的STL提升趨勢;在越過該頻域后,其STL相對不含振子復合結構有降低,降低的幅度和復合結構邊界條件及振子類型有關.此特性與簡單振子情況類似.
3.5 不同周期振子系統聲調控綜合分析
為對照不同振子系統分布對復合結構STL的影響,保持振子系統質量比γ=0.2,取Ns=4,各振子系統特征頻率(簡單振子)或(組合振子)取為300+50(i—1)(Hz),i =1,2,···,Ns.不同周期振子系統分布時復合結構的STL情況如圖13所示.
由圖13可知,幾類周期振子系統對復合結構STL的提升都表現為振子系統特征頻率附近頻域的局部提升,在越過該頻域后,振子系統會降低復合結構的STL,遠離復合結構特征頻率后恢復到無振子情況STL值.對比組合振子系統A,B和簡單振子系統 (Δm=0 和 Δm>0)結果,簡單振子系統總體上可以取得不錯的STL,組合振子系統并不能進一步顯著提升復合結構STL,只在STL提升帶寬上有優勢.在合適的振子參數下,相對簡單振子系統,組合振子系統可拓展復合結構的STL提升帶寬,且不顯著降低復合結構STL水平.
綜合簡單振子系統和組合振子系統結果,在實際工程問題中,采用簡單振子系統預期可以取得合適的STL提升,如果要進一步增大STL提升帶寬,可以考慮使用組合振子.
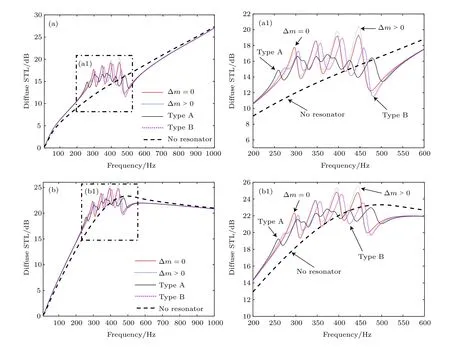
圖13 不同振子系統分布時STL對比 (a),(a1)OU邊界情況;(b),(b1)OB邊界情況;Δm=0 和 Δm>0 對應簡單振子情況NNSR;Type A和Type B對應組合振子情況NNCRFig.13.STL of different resonator system configuration:(a),(a1)OU case;(b),(b1)OB case.Δm=0 and Δm>0 correspond to simple resonator case NNSR.Type A and Type B correspond to composite resonator case NNCR.
4 結 論
含多孔介質復合結構和局域共振周期結構分別有各自的聲學優勢,然而目前對兩者協同效應的研究尚不充分.為取得理想的中低頻隔聲性能,本文提出了一種結合以上兩類聲振抑制方案的復合結構模型,并在中低頻域對其STL進行了理論求解和分析.研究表明,合適地引入和布置周期振子,可以在一定頻域內提升復合結構的STL.這是因為附加的振子系統可以對主結構(薄板)振動產生明顯抑制,合適的振子系統參數,可以抑制某些振動模態的聲輻射,進而提升其STL水平.對比簡單振子和組合振子的結果可知,在實際問題中,若要提升結構在某段頻域的STL,可選取相應特征頻率的簡單振子系統,按照非均勻質量周期布置;如需進一步增大其STL提升帶寬,可考慮使用更為復雜的組合振子系統.盡管本文方法只適用于中低頻問題[35],這些研究結果可以為寬頻減振降噪研究和中低頻減振降噪提供理論參考.
附錄 A (9)式中振子系統相關矩陣
A類組合振子系統的質量矩陣M、阻尼矩陣C和剛度矩陣K為
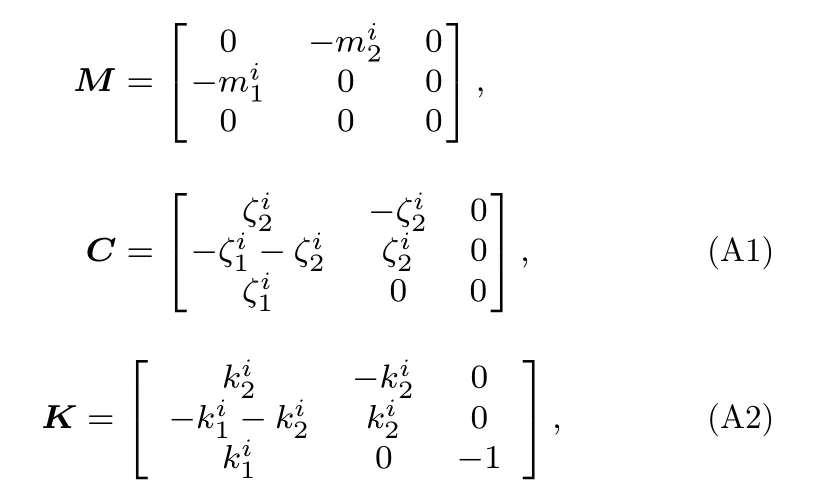
B類組合振子系統的質量矩陣M、阻尼矩陣C和剛度矩陣K為
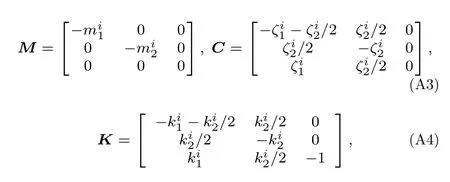
其右端項F為
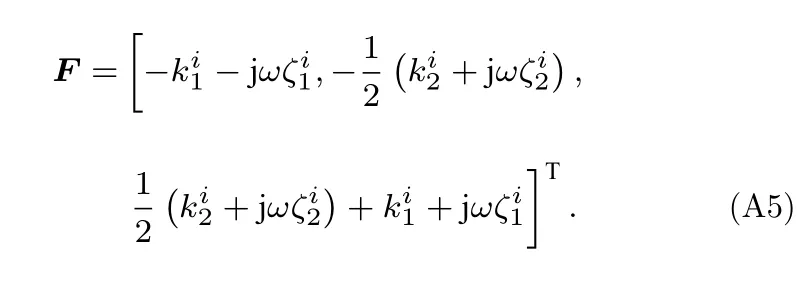
附錄 B (18)式中系數矩陣及力矢量



這里,參數Q0,R0,b1,b2,N0,g,k1z,k2z,k3z,k1,k2和k3都在文獻[3]中給出.
力向量f中非零項為f(1)=jωρi?,f(2)=jωρi×(1-?),f(3)=

