Pohoaev Identities of Elliptic Equations and Systems with Variable Exponents and Some Applications
FENG Tingfu(馮廷福)
(Department of Mathematics,Kunming University,Kunming 650214,China)
Abstract: In this paper,we obtain Pohoaev identities for the elliptic equation and system with variable exponent,respectively.Moreover,nonexistence of nontrivial solutions is derived under some suitable conditions,which extends the results of Dinca and Isaia(2010)and Lopez(2014).
Key words: Pohoaev identity; Nonexistence; Variable exponent; Elliptic equation(system)
1.Introduction and Main Results
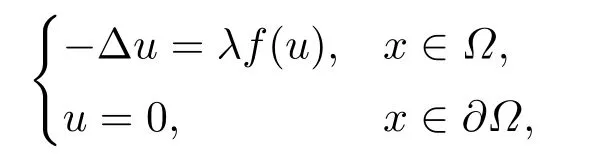
where? ?Rn(n ≥3) is a star-shaped bounded smooth domain with respect to the origin,namely have (x ?0)·ν=x·ν ≥0 for allx ∈??,whereν=ν(x) denotes the unit outward normal atx ∈??,and then applied it to prove nonexistence of nontrivial solutions.This identity was later called the Pohoaev identity and extended to general elliptic equations and systems[2?11].
Elliptic equations with variable exponents as appropriate models in image processing,nonlinear electrorheological fluids and elastic mechanics etc.were extensively studied[12?14].The study of existence and multiplicity of positive solutions for the elliptic equations with variable exponents were given in [15–26] and references therein .
Dinca and Isaia[27]considered the Dirichlet problem

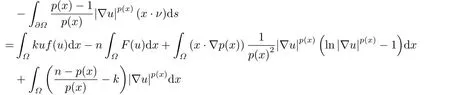
for all k ∈R.
Recently,Lopez[28]considered the elliptic problem with variable exponent

where p(x) and q(x) are ? →R Lipschitz continuous functions and 2 where In this paper,based on the previous works of Dinca and Isaia[27]and Lopez[28],for the weighted functions and more general nonlinear terms in elliptic equation (system) with variable exponent,we consider the following elliptic equation and system with variable exponent,respectively, and Main results are stated in the following. Theorem 1.1Letu ∈W2,p(x)(?)∩W1,p(x)0(?) be a solution to (1.3),1< p(x)< n,a(x)>0,Assume thatf(x,u):?×R→R is continuous and satisfiesF(x,0)=0 forx ∈??.Then then (1.3) has no nontrivial solutions. Remark 1.1In the special casep(x)=2 anda(x)=1,we have by (1.5) that Theorem 1.2Let (u,w)be a pair of solutions to(1.4),1 satisfiesF(x,0,0)=0 forx ∈??.Then where Moreover,ifFu(x,u,w) andFw(x,u,w) satisfy then (1.4) has no nontrivial solutions. Proof of Theorem 1.1Before giving proofs,we need some theory of variable exponent Lebesgue spaces and Sobolev spaces,see [18,29-30] and references therein.For convenience,we give a simple description here. Assume thatp(x) :? →(1,∞) is a Lipschitz continuous function.A variable exponent Lebesgue spaceLp(x)(?) is defined by with the norm A variable exponent Sobolev spaceWm,p(x)(?) is defined by with the norm Denote by(?) the closure ofC0∞(?) inWm,p(x)(?).It is known thatWm,p(x)(?)and(?) are both separable and reflexive Banach spaces. We now prove Theorem 1.1 and give an example. Proof of Theorem 1.1Multiply the equation in (1.3) byuandx·respectively,and integrate it over?.Then there holds and In virtue ofF(x,u)=F(x,0)=0 forx ∈??and the divergence theorem,we obtain which implies Using the left hand side of (2.2) and the divergence theorem,we have In (2.4),we note that Combining (2.4),(2.5) and (2.6),we obtain Substituting (2.3) and (2.7) into (2.2),we obtain (1.5). Since? ?Rnis star-shaped with respect to the origin,it showsx·ν ≥0 forx ∈??.If0 satisfies (1.3),then from (1.5) and (1.6), which is impossible.Then (1.3) has no any nontrivial solutions. Example 2.1Letf(x,u)=λh(x)uq?1in (1.3),whereλ,q ∈R,0< h(x)∈C1(?).Then (1.3) has no any positive solutions under the condition In fact,due to F(x,u)=F(x,0)=0 forx ∈??.Ifu>0 satisfies (1.3),then it concludes from (1.5),(2.9)and 13. A tiny little man: Rumpelstiltskin s size poses many questions unanswered by the text. Is he a dwarf? Most scholars do not think so, but some do. He may also be a demon, an elf or simply a small statured man. Jane Yolen proposes another interesting theory about the tale s meaning and Rumpelstiltskin s origin: that which is a contradiction. Proof of Theorem 1.2Multiply the equation in (1.4) byuandrespectively,and integrate it over?.Then there holds and NotingF(x,u,w)=F(x,0,0)=0 forx ∈??,by the divergence theorem,we obtain and then With the help of (3.1),(3.3) and the divergence theorem,we have We prove (1.7) by substituting (3.4) and (3.5) into (3.3). Let us notex·ν ≥0 forx ∈??.If (u,w)(0,0) satisfies (1.4),then it attains from(1.7) and (1.8) that which is impossible. Example 3.1Letin (1.4),whereλ ∈R,g(x)∈C1(?),then (1.4) has no any positive solutions under the condition Actually,noting that we getF(x,u,w)=F(x,0,0)=0 forx ∈??.If (u,w)>(0,0) satisfies (1.4),then it is obtained from (1.7),(3.6) and that which is a contradiction.

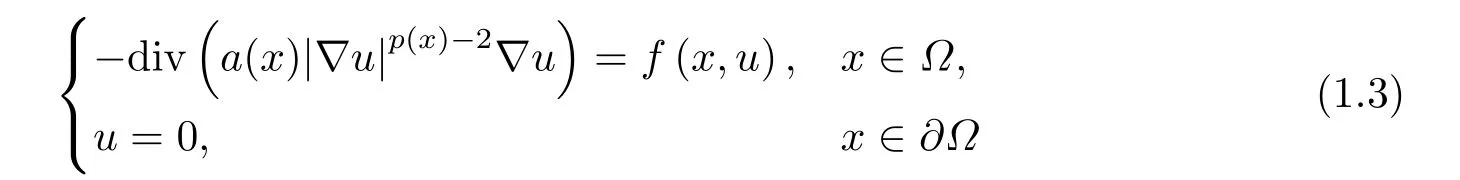
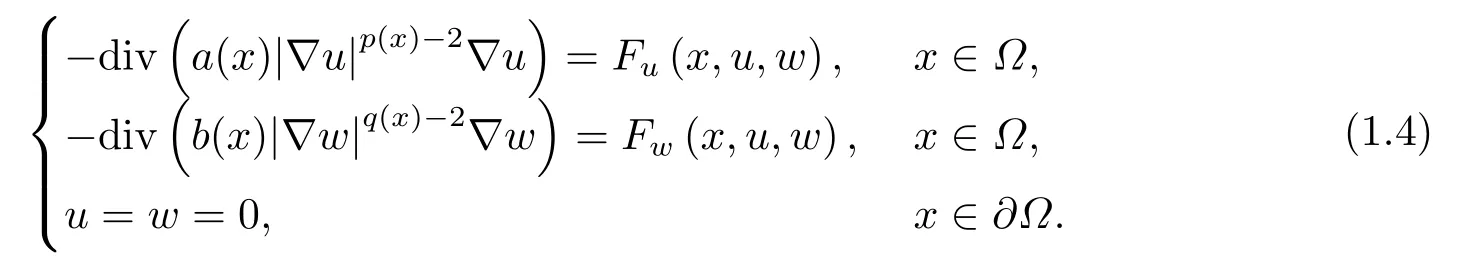
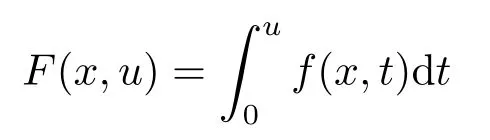

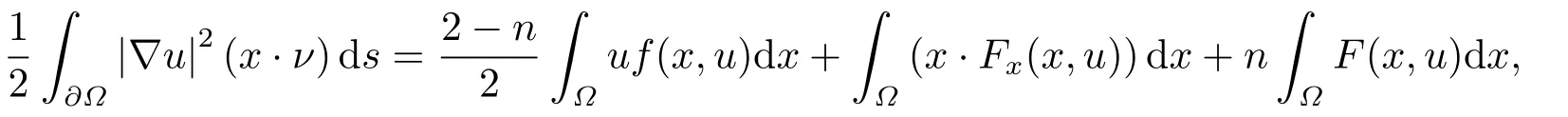

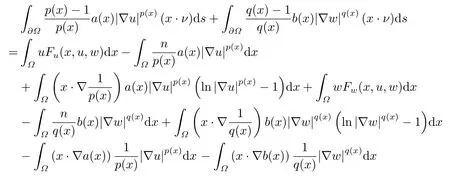
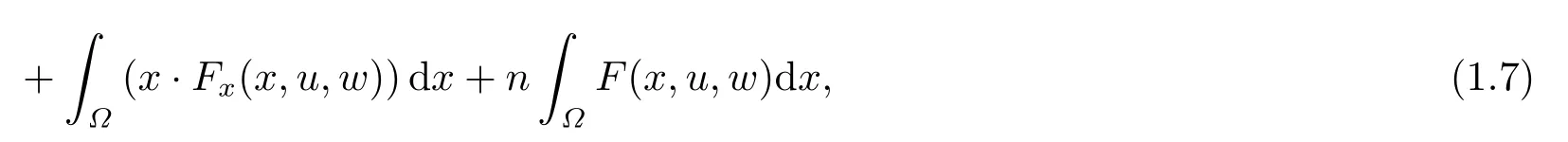
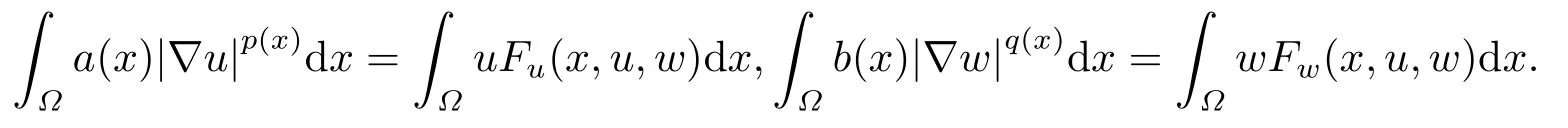

2.Proof of Theorem 1.1
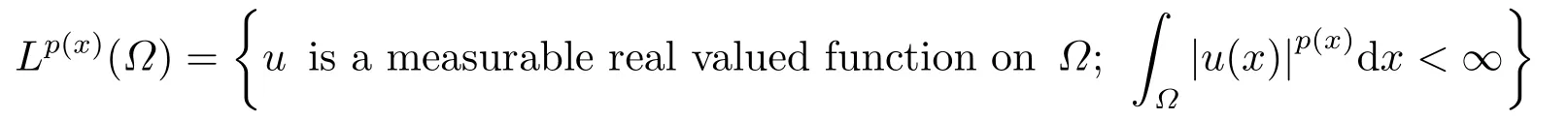

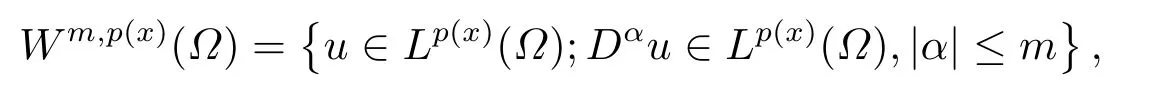


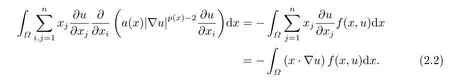
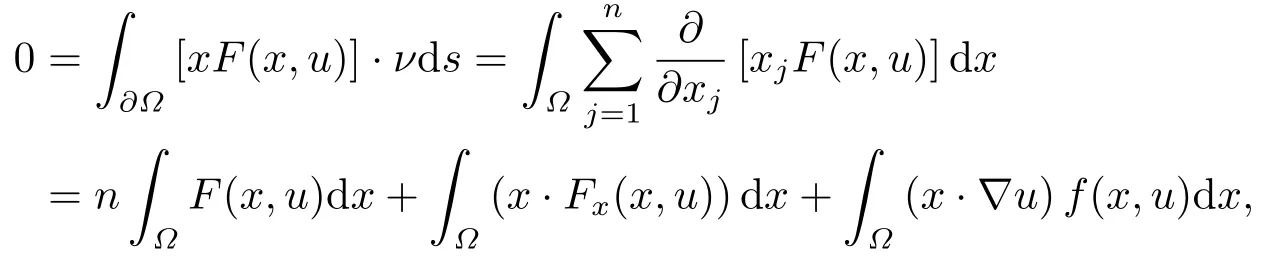

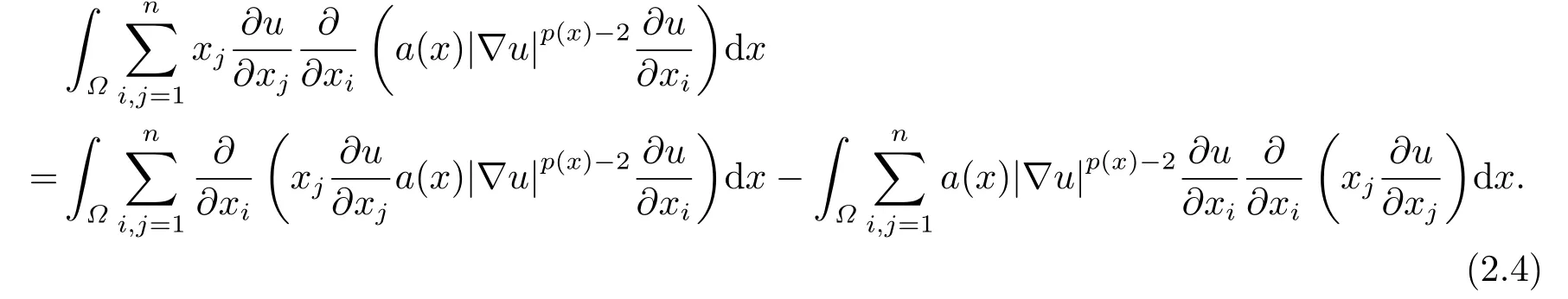
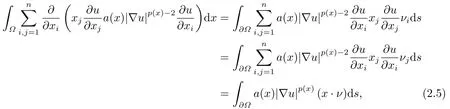
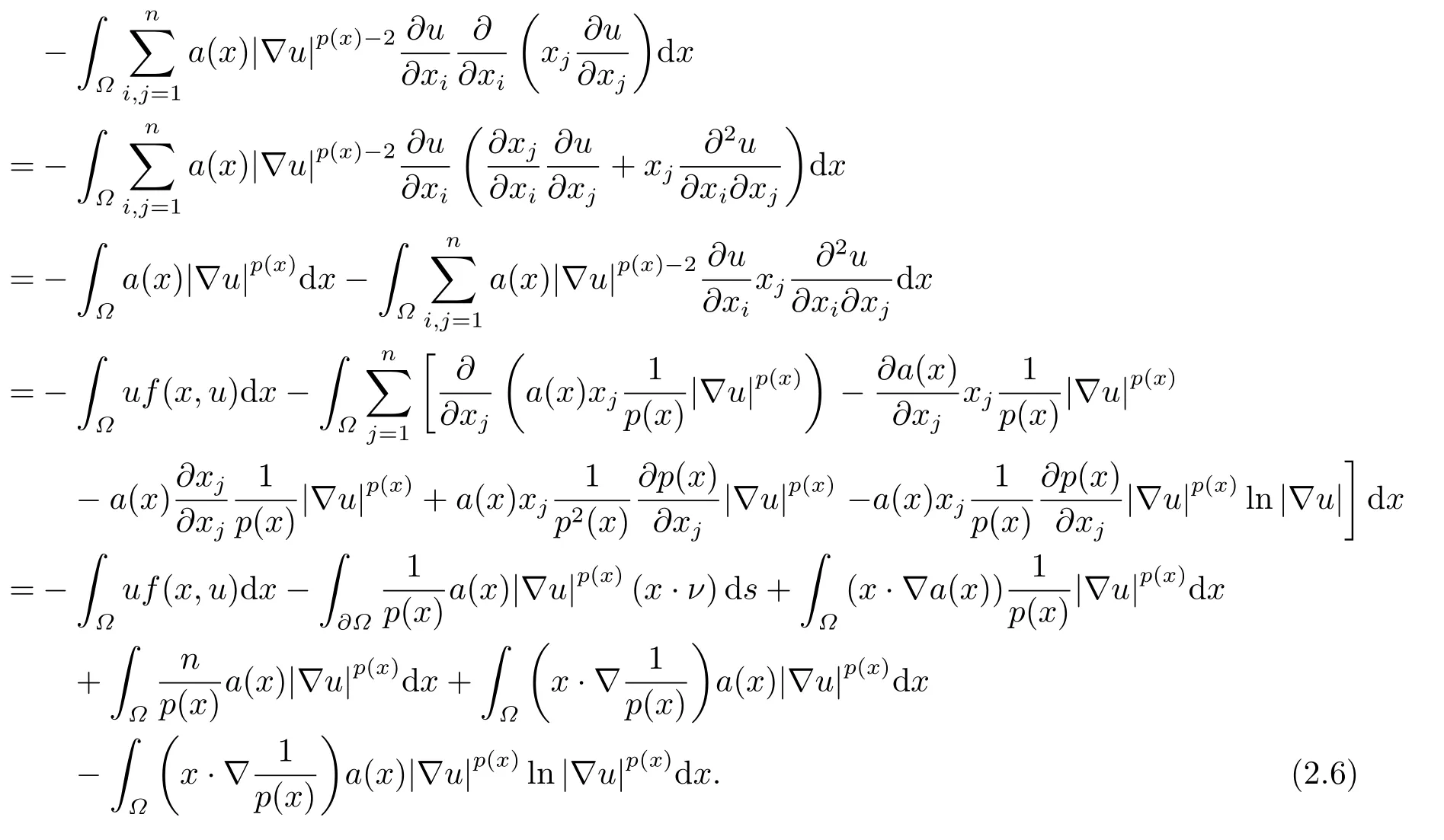

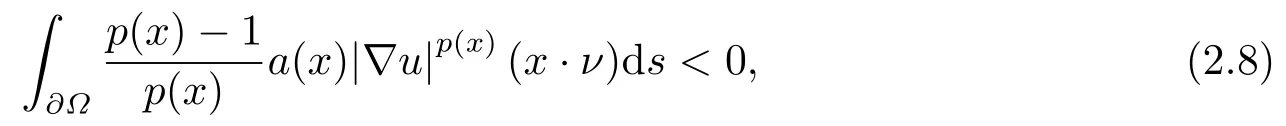
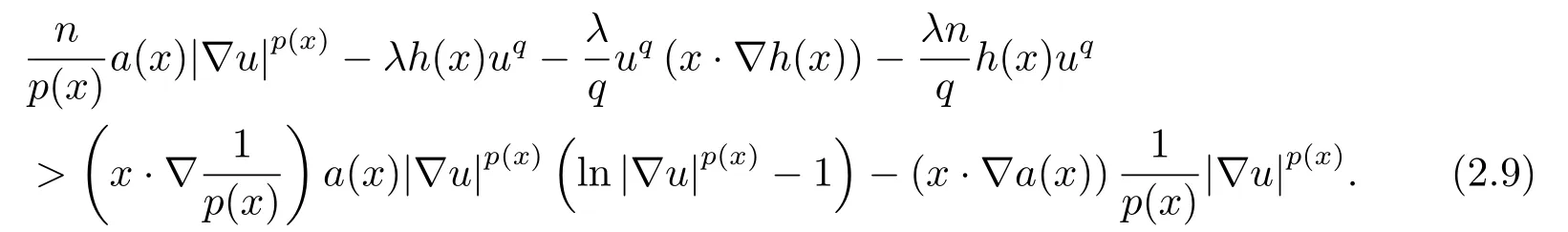
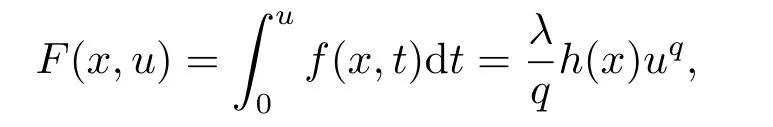
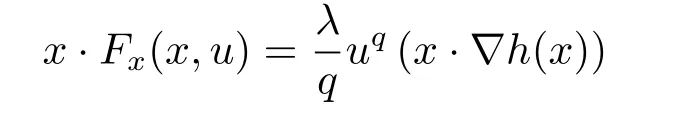
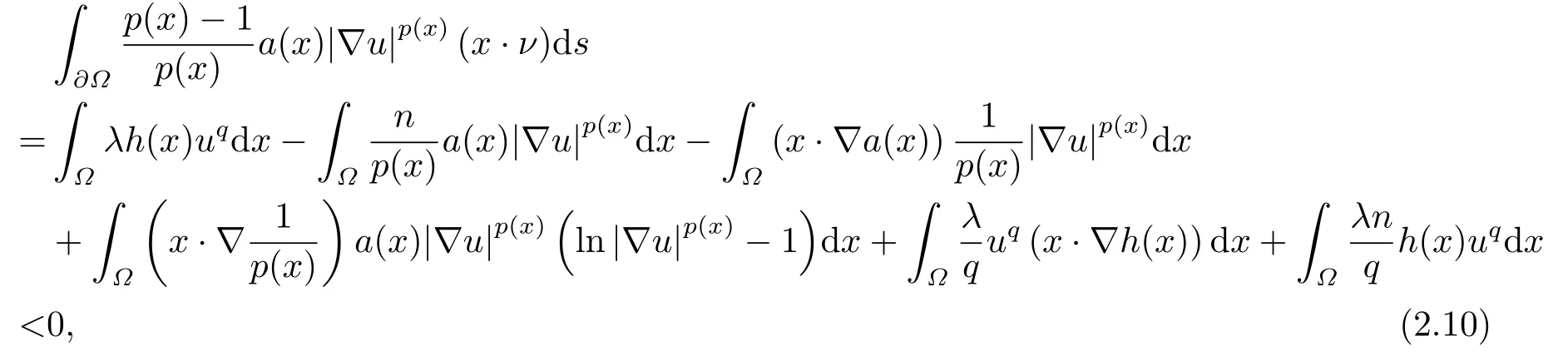
3.Proof of Theorem 1.2
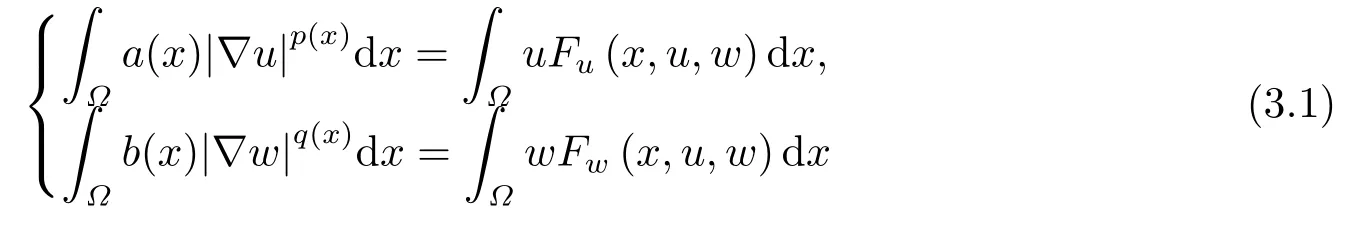
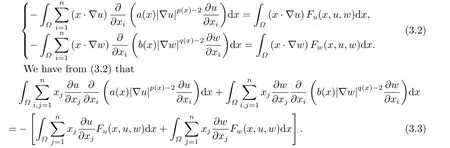
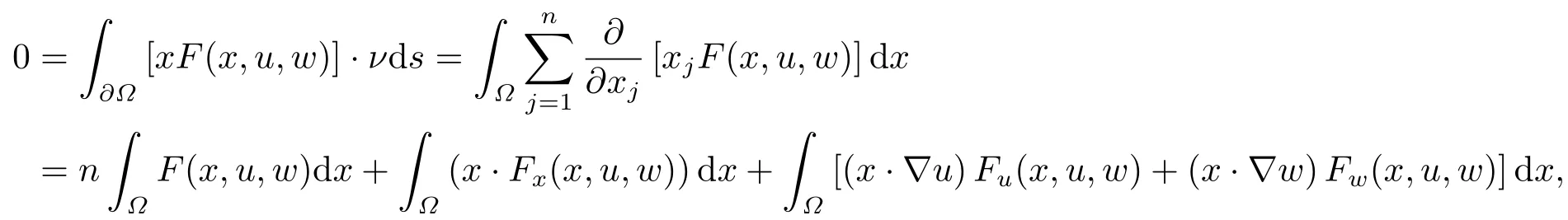
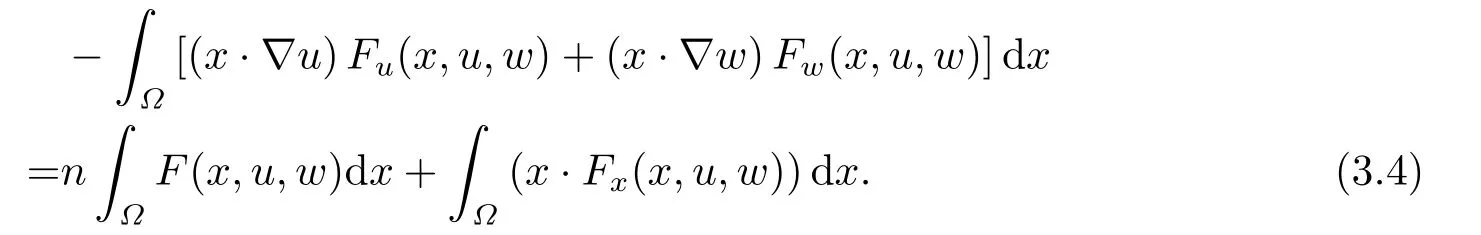
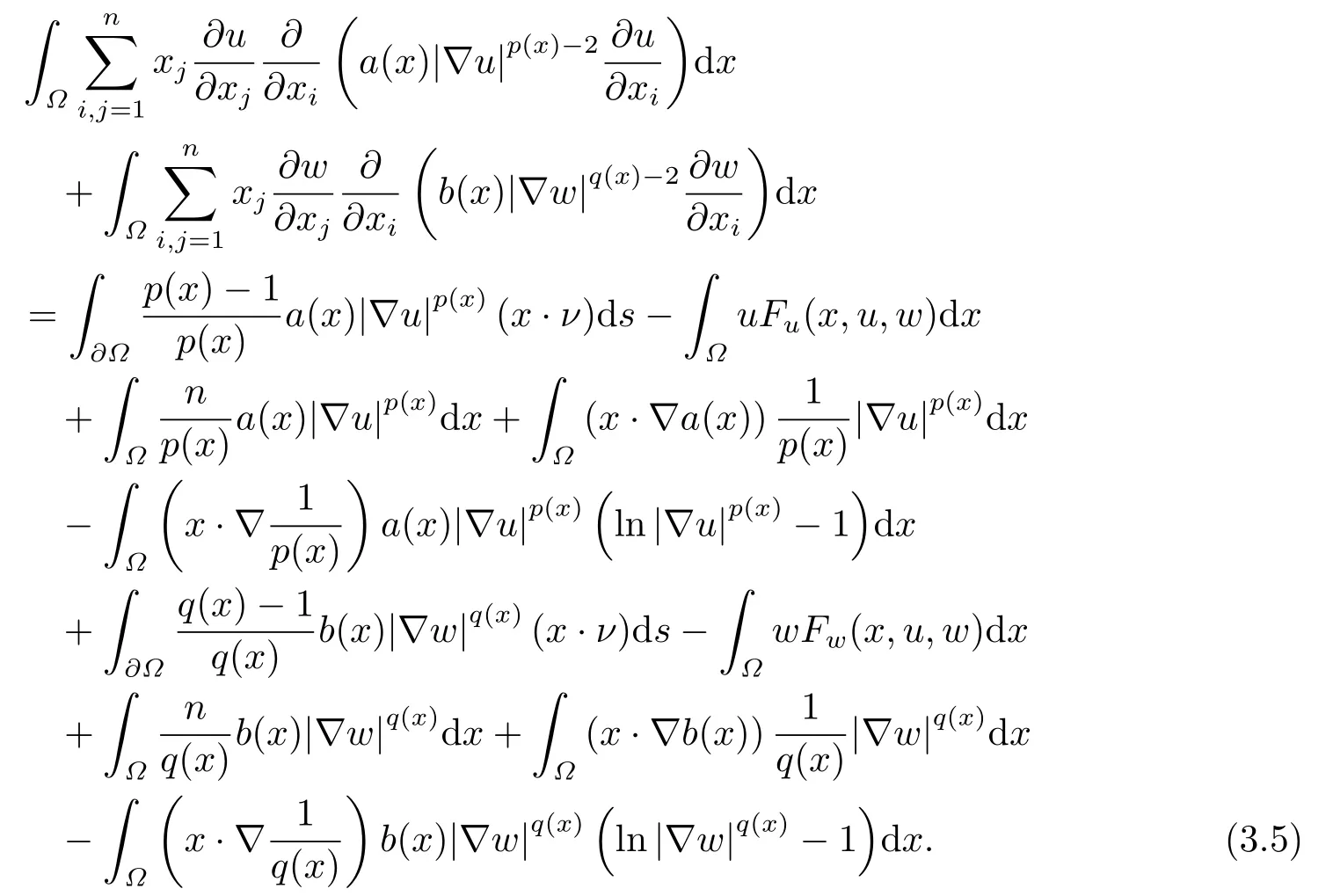
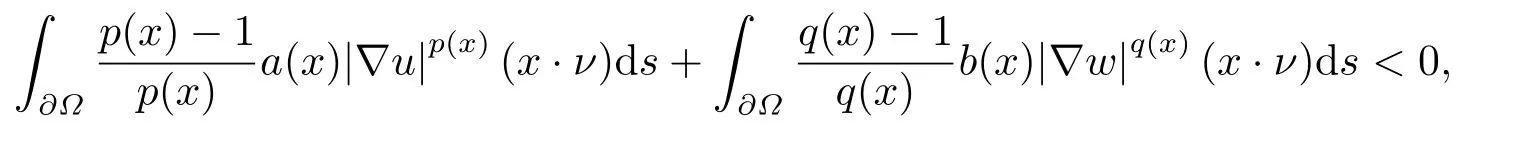


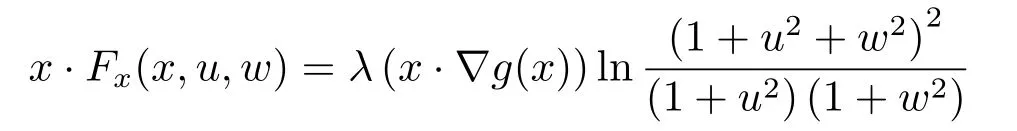
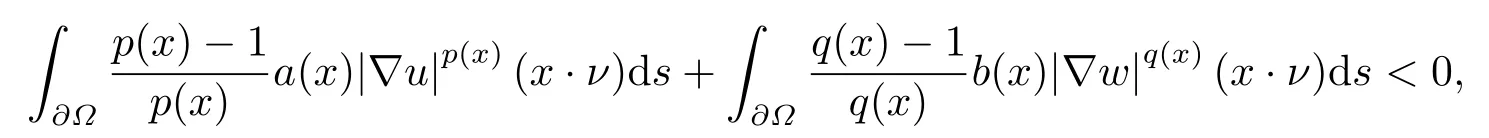
- 應(yīng)用數(shù)學(xué)的其它文章
- Closed-Form Solutions to the Crack and/or Rigid Line Inclusion in 1D Orthorhombic Quasicrystals
- 各向異性橢圓方程雙邊障礙問題解的正則性
- 一類廣義Linard方程周期正解的存在性
- Global Stability of Rarefaction Waves for the One-Dimensional Nonisothermal Compressible Navier-Stokes-Korteweg System
- 廣義嚴(yán)格對(duì)角占優(yōu)矩陣的一種判別法
- 次線性期望空間下END列加權(quán)和的完全收斂性

