韋俊新, 史 炯, 叢 正

(天津航海儀器研究所，天津 300131)

0 引 言

金屬筒形諧振陀螺是固體波動陀螺的一種，利用筒形諧振子被激勵駐波的慣性效應實現陀螺在其敏感軸轉角的測量，該類陀螺用振動元件代替了傳統陀螺的機械轉子，用微幅振動取代了高速旋轉，具有結構強，能耗低，精度高等優點，在兼顧抗高過載、量程大方面表現了巨大的潛力[1]，同時也具有加工簡單，陀螺制造難度低，易于批量化生產等優勢，發展和應用前景極為廣闊[2]。

目前在金屬筒形陀螺及其諧振子振型偏移角的研究方面，國內外許多學者和研究機構已做過不少的工作。Innalabs公司在圓柱形金屬諧振子的底部加工出輪輻狀溝槽，通過減小諧振子的頻率裂解以減小諧振子振型偏角[3]。Watson公司將壓電電極鍍于圓柱殼體的表面，并且將電極設計為分離的小片，可以實現左右的振型校正[4]。國內對于金屬筒形諧振陀螺研究尚處于實驗室樣機階段，尚未見工程化的應用，國防科技大學王旭、陶溢等學者在對諧振陀螺產生振型偏移角的原因及測量方法進行過研究，并從諧振子加工及修調上提出了減小振型偏移角的方法[5,6]。

本文理論分析了金屬筒形諧振子振型偏移的影響因素，通過實驗驗證了振型偏移對諧振子振型對稱性及正反轉差異的影響。根據振型偏移下波節點輸出電壓方程，提出基于前饋調幅調相和基于調制解調反饋控制的兩種不同的振型校正方法，并通過實驗驗證其校正效果。

1 金屬筒形陀螺的基本原理

諧振子底面的壓電電極施以與諧振子的固有頻率同頻的交流電壓信號，由于壓電陶瓷的逆壓電效應，激勵出諧振子的驅動模態(圖1(b))，當角速度輸入時，在哥氏力的作用下敏感出與驅動模態振型相差的敏感模態[7](圖1(c))，壓電電極的正壓電效應檢測敏感模態的振幅，經過外圍解調線路解算出角速度大小。

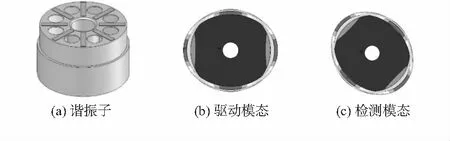
圖1 金屬筒形陀螺核心部件及工作模態

2 振型偏移角的產生原因及影響

諧振子材料的不均勻性和加工誤差等因素，會引起諧振子的頻率裂解和阻尼不均勻[2]，因此諧振子存在剛性軸與阻尼軸[6]，頻率裂解、阻尼不均勻、剛性軸和阻尼軸與激勵軸之間的夾角等因素均引起諧振子的振型偏移角[8]。

2.1 諧振子的頻率裂解

存在頻率裂解情況下，諧振子振型偏移角可以由公式(1)表示[9]

(1)

式中ω0為諧振子的諧振頻率，ΦL-ΦH為兩個剛性軸之間夾角，Δω為頻率裂解，φ0為剛性軸的方位角。

由式(1)表明，頻率裂解引起的振型偏移角的偏移速率大小與頻率裂解以及剛性軸與主振型軸之間的方位夾角8倍正弦值成正比。

設剛性軸方位角為定值，當頻率裂解為0.1,0.5,0.01 Hz時，其振型角度漂移如圖2。

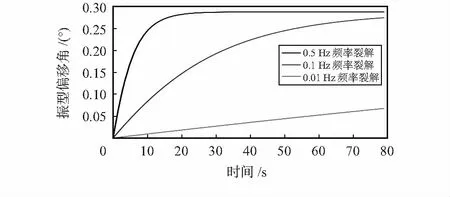
圖2 頻率裂解導致的振型偏移隨時間的變化

如圖2所示，頻率裂解越大，振型偏移角也越大，且振型偏移角隨時間逐漸增大，最終達到穩定。

2.2 諧振子的阻尼不均

阻尼不均勻引起的振型偏移，如式(2)可得

(2)

式中ξ0為均勻的阻尼，γ4為阻尼的不均勻程度，φ0為衰減常數最小阻尼軸方位角。

式(2)表明，金屬筒形陀螺振型偏移角與諧振子阻尼不均勻程度及小阻尼軸與主振型軸之間的方位夾角4倍余弦值成正比。

假設阻尼軸方位角22.5°，當阻尼不均勻為0.01，0.1，0.3時，其振型角度漂移如圖3。

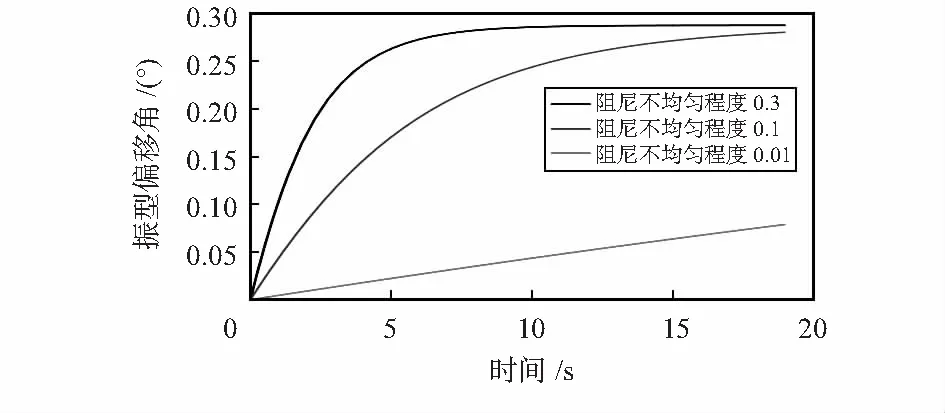
圖3 阻尼不均勻導致的振型的偏移

由圖3可知，阻尼不均勻程度越大，最終振型的偏移速率越大；且振型的偏移量隨時間增大，最終趨于穩定。

2.3 振型偏移角對陀螺性能的影響

選擇實驗室現有的金屬筒形及配套的驅動線路用于測試諧振子振型偏移的程度，用以分析振型偏移造成的影響，諧振子的參數：諧振頻率為5.4 kHz，品質因數Q為7 000，頻率裂解為0.52 Hz。

驅動線路板對置于轉臺的諧振子施加正弦激勵使其達到驅動模態并且使諧振子波腹點振幅保持穩定，轉臺以10″/s2的加速度沿順時針方向轉動至10°/s速率，采集節點電壓信號；同樣，轉臺以相同加速度沿逆時針方向轉動至10°/s速率，采集節點電壓信號。結果如圖4所示。

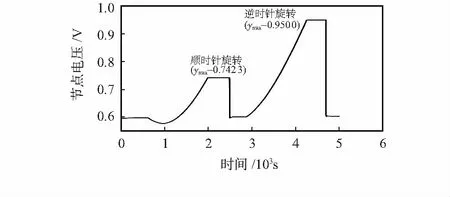
圖4 存在角度偏移條件下順逆時針旋轉節點電壓輸出

由圖4可知：1)順時針旋轉轉臺時，節點電壓存在先降后升的趨勢，說明該方向旋轉時，45°處壓電電極處的振動經歷了先減弱后加強的趨勢，而逆時針旋轉無此現象；2)順逆旋轉最終角速率均為10°/s，但節點電壓輸出大小不同，逆時針旋轉時節點電壓輸出比順時針旋轉節點電壓大近210 mV。

本文利用德國Polytec公司的PSV—400型多普勒激光測振儀對金屬諧振子唇沿部分的徑向振幅進行測量。諧振子環向測試點數400，得到的振幅數據如圖5所示。

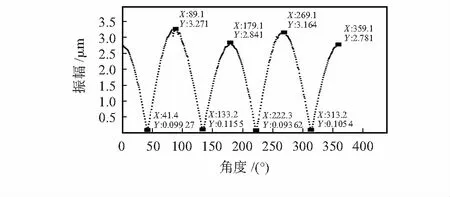
圖5 諧振子環向振幅數據

由圖5可知，諧振子波腹點與波節點振幅及所處角度如表1、表2所示。

表1 波節點振幅及所處角度

表2 波腹點振幅及所處角度

由圖4、圖5和表2可以看出：諧振子4個波腹點的振幅大小并不一致，最大相差0.43 μm，說明振型有畸變，同時駐波振型節點偏離節點檢測壓電電極所在位置。

3 振型校正方法

校正諧振子振型的方法，從諧振子方面主要是提高加工制造精度、降低材料的不均勻性，采用更合適的修調方案，比如去質量修調方案[10]等，降低諧振子的頻率裂解，本文從線路角度，提出兩種振型校正方法，以進一步減小振型偏移。

3.1 前饋調軸法

受到激發的諧振子會產生四波腹振動，其環向振型為

Uo(t)=Acos 2(θ-α)sin(ωpt+β)

(3)

式中ωp為諧振子的諧振頻率，α為諧振子的振型偏移角，理想情況下α=0。

已知當兩個同頻率，同相位的外界激勵力(F1，F2)同時作用于殼體的0°電極軸和45°電極軸時，相當于一個幅值為F3的外界激勵力單獨作用于殼體環向一點[11]。改變F1和F2的比值，就可以改變θ

U3=U1+U2=Ecos 2(θ-θE)cosωt

(4)

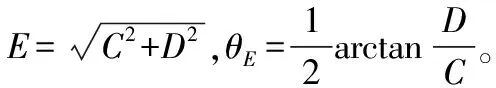
改變C和D幅值比值，就可以使殼體發生環向振型的移動，選取一個合適的比值，令α-θE=0，使殼體發生的進動抵消振型的偏移，進而消除偏移量。

因此，在諧振子選取一點施加一定幅值激勵信號，通過調節此激勵信號的幅值和相位，糾正諧振子振型的偏移誤差，圖6是線路控制方案。

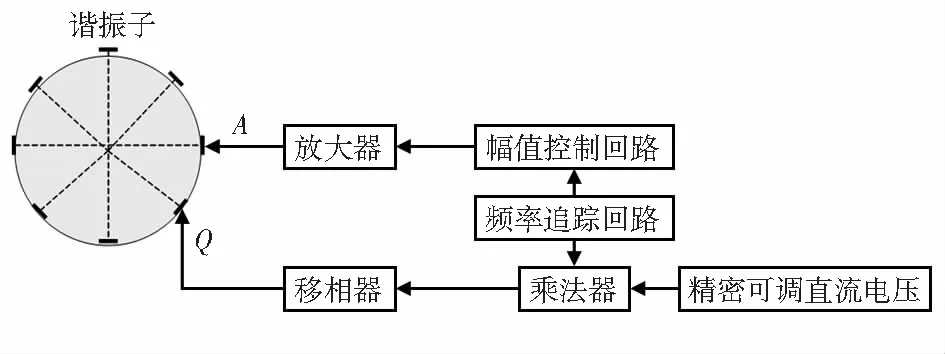
圖6 前饋調振型軸線路控制方案

該方案可較為徹底的對振型進行調整，但同時仍存在問題：由前文所述，頻率裂解和阻尼不均勻引起的諧振子振型的偏移隨時間而變化，前饋調軸法無法隨時感測諧振子振型角度的改變，以自動調整施加校正電壓Q的幅值和相位，不利于金屬筒形陀螺在工程上的應用。

3.2 反饋調軸法

反饋調軸法是通過解調表頭輸出信號q，分解其同相和正交分量，分別進行控制后通過調制合成為反饋控制信號，以抑制諧振子振型的偏移。其線路控制基本示意如圖7所示。

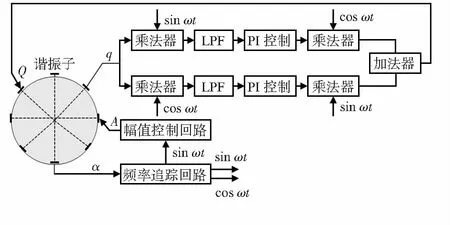
圖7 反饋調振型軸線路控制方案

檢測端輸出的振動信號V可以表示為[12]

V=KΩZsin(ωt+φsense)+VKsin(ωt+φq)+

VIsin(ωt+φsense)

(5)

式中KΩZsin(ωt+φsense)為角速度耦合信號，VKsin(ωt+φq)是正交誤差信號，VIsin(ωt+φsense)是同相誤差信號。

當無角速度輸入時即ΩZ=0，則此時振動信號可以表示為

V=VKsin(ωt+φq)+VIsin(ωt+φsense)

(6)

通過sinωt和cosωt解調和濾波，可得

I=VKsinφq+VIsinφsense

(7)

K=-VKcosφq-VIcosφsense

(8)

通過sinωt和cosωt調制和相加，可得驅動信號Q

Vdrive=-VKcos(ωt+φq)-VIcos(ωt+φsense)

(9)

該驅動信號反映到測量點節點電壓處時，可得

(10)

該信號可有效消除原節點電壓信號V，即消除了振型的偏移角。

所提方案的優點是能即時的感知振型偏移造成的節點電壓的變化，通過反饋回路消除振型偏移角，彌補前饋調軸方案的不足，提升了在陀螺工程化應用價值。但所提方案不足之處在于，由于對諧振子加工，裝配誤差等因素，正交誤差信號與同相誤差信號可能會附加誤差項，故對振型的調整并不能很徹底。

4 試驗驗證

采用圖6所示的流程圖設計了前饋調軸板，并進行了實驗，結果如圖8(a)所示。

同樣，利用激光測振儀對調軸后的諧振子唇沿振型進行了測量，得到環向振幅與振型分布，如圖8(b)所示。

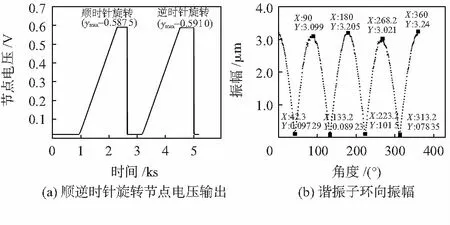
圖8 前饋調軸后實驗結果

由圖8(b)可知，諧振子波腹點與波節點振幅及所處角度如表3、表4所示。

表3 波節點振幅及所處角度

表4 波腹點振幅及所處角度

通過前饋調軸之后，對比表2和表4；表3和表5可見：1)諧振子振型相對調軸之前偏移了0.8°～0.9°；2)改善了振型4個波腹振幅不一致的問題，4個波腹點振幅最大相差0.219 μm，比調軸前的差值減小了近50 %；3)節點電壓的振幅明顯降低。說明前饋調軸方案能夠有效地減小諧振子振型以及振幅的偏移。

采用圖7設計了反饋調軸板，實驗測試調軸效果如圖9(a)所示，其振型分布圖如圖9(b)。

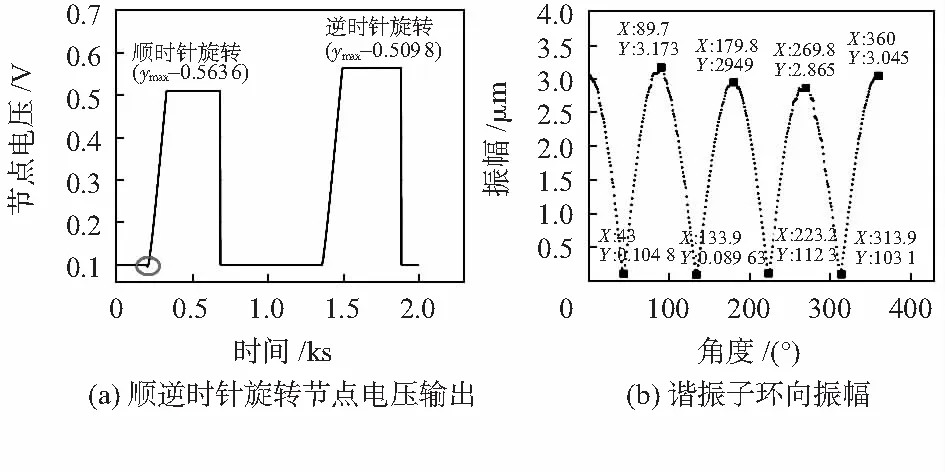
圖9 反饋調軸后實驗結果

由圖9(b)可知，諧振子波腹點與波節點振幅及所處角度如表5、表6所示。

表5 波節點振幅及所處角度

表6 波腹點振幅及所處角度

通過反饋調軸之后，與調軸之前相比，可得：1)從波腹和波節所處的角度可知諧振子振型相對調軸之前移了0.6°～0.7°；2)振型四個波腹點振幅相差最大值是0.308 μm，與調軸前相比已有所減少；3)由圖10可知，順時針旋轉時依然存在先下降后上升的現象，但相比調軸前已經減弱很多。

經實驗驗證，前饋調軸及反饋調軸均能改善振型偏移的問題，但是反饋調軸效果弱于前饋調軸的效果。

5 結 論

本文分析了金屬筒形諧振子振型偏移的原因，利用實驗驗證了諧振子振型偏移造成的影響，并從線路控制方面提出了兩種解決振型偏移的方案，通過實驗驗證，該兩種方案能夠有效地校正振型偏移，進而減小振型偏移的造成的影響，并分析了兩種方案的優缺點，為后續對金屬筒形諧振陀螺研究奠定了基礎。